2. 山东交通学院 海运学院, 济南 264200
2. School of Maritime, Shandong Jiaotong University, Jinan 264200, China
阻尼材料可以将结构的机械能转化为热能耗散. 约束阻尼是指将黏弹性阻尼材料固结在基体和刚度较大的材料之间,基体为基层,刚度较大的材料为约束层. 当基体振动时,基层与约束层产生相对运动,黏弹性阻尼材料发生剪切变形使一部分机械能发生损耗. 约束阻尼结构形式较为简单,阻尼效果好,振动能量耗散剧烈,易于实现,广泛地应用在汽车、建筑、机械、航天、船舶、仪表仪器中. 目前,对约束阻尼的研究主要集中在板[1]、壳[2-4]、梁[5]、杆[6]等单元上. 对敷设约束阻尼圆柱壳的研究方法可分为有限元法和解析法两种. Ruzzene等[7]和Wang等[8]通过有限元法计算了敷设约束阻尼圆柱壳的固有频率和损耗因子,并且分析了各参数对于圆柱壳固有频率的影响. 王淼等[9]和章艺等[10]也通过有限元法对约束阻尼圆柱壳的频率特性进行分析. 有限元方法虽然对圆柱壳结构要求低,适用范围广,但是在参数分析时比较困难,并且由于引入离散变量使自由度过多而造成计算困难,在高频时计算精度较低.
对敷设约束阻尼圆柱壳进行参数分析时一般采用解析法,现在较为成熟的解析法有传递矩阵法、瑞利法、带有分布参数的传递函数法等. 文献[11-13]运用瑞利法分析了约束阻尼圆柱壳和部分敷设约束阻尼圆柱壳的频率特性,给出了圆柱壳振动响应的计算方法,并且分析了约束阻尼各参数对圆柱壳阻尼效果的影响. 向宇等[14-15]针对敷设约束阻尼圆柱壳的振动特性,利用改良的传递矩阵法进行分析,可以求出各种边界条件下圆柱壳的振动. 这种方法在求解敷设约束阻尼圆柱壳的自由振动时较为精确. 但是由于引入各层内力,传递矩阵是一个12维的矩阵,计算量增加,在分析圆柱壳的受迫振动时比较困难. 李恩奇等[16]利用分布参数法提出了一种分析约束阻尼圆柱壳动力学问题的传递函数法,分布参数的引入有利于拓展传递函数法的应用范围;但是该方法对于边界条件的描述是通过位移间接进行的,在求解不同边界条件下的圆柱壳振动特性时比较困难,而且该方法也无法计算圆柱壳的频率响应.
综上所述,虽然人们对敷设约束阻尼圆柱壳的振动特性进行了深入的研究,并且提出了不同的方法. 但是这些方法有以下问题: 1) 对于圆柱壳的振动特性集中在自由振动特性的研究上,没有分析敷设约束阻尼前后圆柱壳的响应问题; 2) 对约束阻尼结构做参数分析时,仅把固有频率下的损耗因子作为评价阻尼效果的唯一标准,无法分析在一定频带范围内的阻尼效果.
本文从圆柱壳基本方程出发,首先,推导出敷设约束阻尼圆柱壳系统的应变能和动能表达式;然后,应用哈密顿原理结合瑞利-李兹求取圆柱壳的动力学方程,并对其进行求解,得出敷设约束阻尼圆柱壳的固有频率和损耗因子,采用模态叠加法求得系统在受迫振动下的频率响应;最后,引入能量耗散系数表示敷设约束阻尼圆柱壳在一定频带范围内的阻尼效果,分析约束阻尼结构各参数的变化对于圆柱壳阻尼效果的影响.
1 动能及应变能约束阻尼圆柱壳结构如图 1所示,3层结构分别为基层、阻尼层和约束层. 为了简化,做如下假设:1)基层和约束层满足圆柱薄壳假设;2)各层接触面之间无相对滑动,完全黏结,各层之间位移连续,3层材料沿径向位移相同;3)由于阻尼材料密度较低,其面内惯量忽略不计,只考虑阻尼层的径向惯量;4)黏弹性阻尼层只考虑剪切变形,忽略其抗拉、抗弯刚度. 曲线坐标系的原点在圆柱壳端面的圆心处,其中圆柱壳母线方向为x轴,圆周方向为θ轴,圆柱壳中面外法线的方向为z轴. 本文中符号h和R分别代表壳体的厚度和半径,各式下标或者上标中的s、v和c分别代表基层、阻尼层和约束层.壳体中曲面上一点的轴向、切向、法向位移分别为u、v、w.

|
图 1 约束阻尼圆柱壳几何示意图 Figure 1 Cylindrical shell with CLD |
根据圆柱薄壳假设,基层和约束层的应变-位移关系可以表示为
| $\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{xi}} = \varepsilon _{xi}^0 + zk_{xi}^0,} \\ {{\varepsilon _{\theta i}} = \varepsilon _{\theta i}^0 + zk_{\theta i}^0,} \\ {{\varepsilon _{x\theta i}} = \varepsilon _{x\theta i}^0 + zk_{x\theta i}^0.} \end{array}} \right.$ | (1) |
式中:i=s,c; εji0为膜应变分量,各分量表达式为
| $\varepsilon _{xi}^0 = \frac{{\partial {u_i}}}{{\partial x}},\varepsilon _{\theta i}^0 = \frac{{\partial {v_i}}}{{{R_i}\partial \theta }} + \frac{w}{{{R_i}}},\varepsilon _{x\theta i}^0 = \frac{{\partial {v_i}}}{{\partial x}} + \frac{{\partial {u_i}}}{{{R_i}\partial \theta }};$ |
kji0为弯曲应变分量,各分量表达式为
| $k_{xi}^0 = - \frac{{\partial _w^{^2}}}{{\partial {x^2}}},{\text{ }}k_{\theta i}^0 = \frac{{\partial {v_i}}}{{R_i^2\partial \theta }} - \frac{{{\partial ^2}w}}{{R_i^2\partial {\theta ^2}}},k_{x\theta i}^0 = \frac{{\partial {v_i}}}{{{R_i}\partial x}} - \frac{{2{\partial ^2}w}}{{{R_i}\partial x\partial \theta }}.$ |
基层和约束层的应变势能为
| $\begin{gathered} {U_i} = \frac{{{h_i}}}{2}\int_{2\pi }^0 {\int_0^l {[\frac{{{E_i}}}{{1 - {\mu _i}^2}}(\varepsilon _{xi}^2 + \varepsilon _{\theta i}^2 + 2{\mu _i}{\varepsilon _{xi}}{\varepsilon _{\theta i}}) + } } \hfill \\ {G_i}/2\varepsilon _{x\theta i}^2]{R_i}dxd\theta . \hfill \\ \end{gathered} $ | (2) |
式中:Ei、 μi和Gi分别表示第i层的弹性模量、泊松比和剪切模量.
基层和约束层的动能为
| ${T_i} = \frac{{{\rho _i}{h_i}}}{2}\int_0^l {\int_0^{2\pi } {({{\dot u}^2}_i + {{\dot v}^2}_i + {{\dot w}^2}){R_i}dxd\theta .} } $ | (3) |
阻尼层应变-位移关系为
| $\left\{ {\begin{array}{*{20}{c}} {\varepsilon _{xz}^v = \beta _x^v + \frac{{\partial w}}{{\partial x}},} \\ {\varepsilon _{\theta z}^v = \beta _\theta ^v - \frac{{{v_v}}}{{{R_v}}} + \frac{1}{{{R_i}}}\frac{{\partial w}}{{\partial \theta }}.} \end{array}} \right.$ |
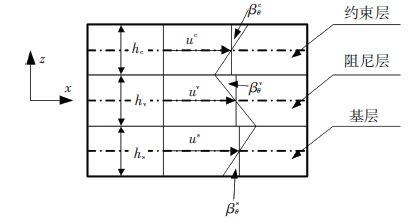
式中:εxzv、εθzv分别为阻尼层沿x、θ方向剪切应变,βθi为第i层横截面沿θ方向的转角(i=s,c,v). 各转角和约束阻尼层间沿x方向位移关系如图 2所示.
|
图 2 约束阻尼沿x方向层间位移关系 Figure 2 Displacement relationship of CLD among layers along the x direction |
根据图 2,由几何关系可得各层沿x方向位移关系:
| $\left\{ {\begin{array}{*{20}{c}} {{u_c}\left( {x,\theta } \right) - \frac{{{h_c}}}{2}\beta _x^c\left( {x,\theta } \right) = {u_v}\left( {x,\theta } \right) + \frac{{{h_v}}}{2}\beta _x^v\left( {x,\theta } \right),} \\ {{u_s}\left( {x,\theta } \right) + \frac{{{h_s}}}{2}\beta _x^c\left( {x,\theta } \right) = {u_v}\left( {x,\theta } \right) - \frac{{{h_v}}}{2}\beta _x^v\left( {x,\theta } \right).} \end{array}} \right.$ | (4) |
同理,可得各层沿θ方向的位移关系:
| $\left\{ {\begin{array}{*{20}{c}} {{v_c}\left( {x,\theta } \right) - \frac{{{h_c}}}{2}\beta _\theta ^c\left( {x,\theta } \right) = {v_v}\left( {x,\theta } \right) + \frac{{{h_v}}}{2}\beta _\theta ^v\left( {x,\theta } \right),} \\ {{v_s}\left( {x,\theta } \right) + \frac{{{h_s}}}{2}\beta _\theta ^s\left( {x,\theta } \right) = {v_v}\left( {x,\theta } \right) - \frac{{{h_v}}}{2}\beta _x^v\left( {x,\theta } \right).} \end{array}} \right.$ | (5) |
将式(4)和(5)整理可得阻尼层沿θ、x轴的中面位移和横向法线绕θ、x轴的转角为
| $\left\{ {\begin{array}{*{20}{c}} {{u_v}\left( {x,\theta } \right) = \frac{1}{2}[({u_c} - \frac{{{h_c}}}{2}\beta _x^c) + ({u_s} + \frac{{{h_s}}}{2}\beta _x^s)],} \\ {{v_v}\left( {x,\theta } \right) = \frac{1}{2}[({v_c} - \frac{{{h_c}}}{2}\beta _\theta ^c) + ({v_s} + \frac{{{h_s}}}{2}\beta _\theta ^s)],} \\ {\beta _x^v\left( {x,\theta } \right) = \frac{1}{{{h_v}}}[({u_c} - \frac{{{h_c}}}{2}\beta _x^c) - ({u_s} + \frac{{{h_s}}}{2}\beta _x^s)],} \\ {\beta _\theta ^v\left( {x,\theta } \right) = \frac{1}{{{h_v}}}[({v_c} - \frac{{{h_c}}}{2}\beta _\theta ^c) - ({v_s} + \frac{{{h_s}}}{2}\beta _\theta ^s)].} \end{array}} \right.$ | (6) |
对于黏弹性阻尼层,其本构方程为
| $\left\{ {\begin{array}{*{20}{c}} {\tau _{xz}^v = {G^v}\varepsilon _{xz}^v,} \\ {\tau _{\theta z}^v = {G^v}\varepsilon _{\theta z}^v.} \end{array}} \right.$ |
式中:τxzv、τθzv分别表示沿x、θ轴的剪切应力;Gv表示阻尼材料的复剪切模量,且
| ${G^v} = G_1^v + iG_2^v = G\left( \omega \right)(1 + gi)$ |
G1v为复剪切模量的实部,也称为储能剪切模量;G2v为复剪切模量的虚部,它决定了黏弹性阻尼材料受到剪切变形时转换成热能的能量损耗,所以称为损耗剪切模量;g为黏弹性阻尼材料的阻尼系数.
阻尼层剪切应力做功为
| $\begin{gathered} {W_v} = \frac{1}{2}\int_{ - \frac{{{h_v}}}{2}}^{\frac{{{h_v}}}{2}} {\int_0^l {\int_0^{2\pi } {(\tau _{xz}^v\varepsilon _{xz}^v + \tau _{\theta z}^v\varepsilon _{\theta z}^v){R_v}dxd\theta dz = } } } \hfill \\ {U_v} + {W_1}. \hfill \\ \end{gathered} $ | (7) |
式中:Wv是一个复数,其实部Uv表示能量的存储,为阻尼层的应变势能Uv;虚部W1表示能量的耗散,阻尼力所做的功为Wv1=-W1.
根据假设(3)可得阻尼层的动能
| ${T_v} = \frac{1}{2}{\rho _v}{h_v}{R_v}\int_0^{2\pi } {\int_0^l {{{\dot w}^2}dxd\theta } } .$ | (8) |
由此可得系统的势能为
| $U = {U_c} + {U_v} + {U_s}.$ | (9) |
系统的变形能与耗散能之和为
| $W = {U_c} + {W_v} + {U_s}.$ | (10) |
系统的动能为
| $T = {T_c} + {T_s} + {T_v}.$ | (11) |
圆柱壳单边可能出现的约束条件有自由(F)、固支(C)、简支(SS). 因此圆柱壳的边界条件可以分为:自由-自由(F-F)、自由-固支(F-C)、自由-简支(F-SS)、固支-固支(C-C)、固支-简支(C-SS)、简支-简支(SS-SS)6种. 根据式(6)可知,阻尼层的位移可由基层和约束层的位移表示. 当敷设约束阻尼圆柱壳以某一频率ω振动时,将位移函数沿壳体圆周方向展开成富氏级数,而沿轴向则用某一系列正交函数系进行展开[17]. 敷设约束阻尼圆柱壳的基层和约束层中面模态振型函数可以表示为
| $\begin{gathered} u_{ij}^s\left( {x,\theta ,t} \right) = X_i^{{u^s}}\left( x \right)cosj\theta p_{ij}^s\left( t \right) = U_{ij}^s\left( {x,\theta } \right)p_{ij}^s\left( t \right), \hfill \\ v_{ij}^s\left( {x,\theta ,t} \right) = X_i^{{v^s}}\left( x \right)sinj\theta r_{ij}^s\left( t \right) = V_{ij}^s\left( {x,\theta } \right)r_{ij}^s\left( t \right), \hfill \\ u_{ij}^c\left( {x,\theta ,t} \right) = X_i^{{u^c}}\left( x \right)cosj\theta p_{ij}^c\left( t \right) = U_{ij}^c\left( {x,\theta } \right)p_{ij}^c\left( t \right), \hfill \\ v_{ij}^c\left( {x,\theta ,t} \right) = X_i^{{v^c}}\left( x \right)sinj\theta r_{ij}^c\left( t \right) = V_{ij}^c\left( {x,\theta } \right)r_{ij}^c\left( t \right), \hfill \\ {w_{ij}}\left( {x,\theta ,t} \right) = X_i^w\left( x \right)cosj\theta {s_{ij}}\left( t \right) = {W_{ij}}\left( {x,\theta } \right){s_{ij}}\left( t \right). \hfill \\ \end{gathered} $ |
式中:每一组(i,j)对应一个固有频率;i表示周向波数;j表示轴向半波数;pijs(t)、rijs(t)、pijc(t)、rijc(t)、sij(t)是模态坐标,为时间的待求函数;Uijs、Vijs、Uijc、Vijc、Wij为满足边界条件的位移形状函数,也就是在该频率下的主振型;Xius(x)、Xivs(x)、Xiuc(x)、Xivc(x)、Xiw(x)为基层和约束层沿中面位移振型. 将中面位移沿轴向采用梁函数进行构造时,沿u、v、w 3个方向轴向位移形状函数满足以下关系式[18]:
| $X_i^u\left( x \right) = \frac{{\partial \phi \left( x \right)}}{{\partial x}},X_i^v\left( x \right) = \phi \left( x \right),X_i^w\left( x \right) = \phi \left( x \right).$ |
式中Φ(x)为轴向函数,采用梁函数进行构造[19],
| $\begin{gathered} \phi \left( x \right) = {a_1}cosh\left( {rx/L} \right) + {a_2}cos\left( {rx/L} \right) - \hfill \\ \lambda ({a_3}sinh\left( {rx/L} \right) + {a_4}sin\left( {rx/L} \right)); \hfill \\ \end{gathered} $ |
各参数a1、a2、a3、a4是由边界条件确定,其值是常数0或者±1; r是由具体函数确定的常数; λ是由r确定的. 各参数在具体边界条件下的表达式见文献[19].
2.2 动力学方程应用哈密顿原理结合瑞利-李兹法求解敷设约束阻尼圆柱壳的动力学方程. 根据2.1节模态振型函数,可以表示出各层的位移为
| $\left\{ {\begin{array}{*{20}{l}} {{u^s} = \sum\limits_{i = 0}^\infty {\sum\limits_{j = 0}^\infty {U_{ij}^s\left( {x,\theta } \right)p_{ij}^s\left( t \right) = U_s^T\left( {x,\theta } \right){p^s}\left( t \right),} } } \\ {{u^s} = \sum\limits_{i = 0}^\infty {\sum\limits_{j = 0}^\infty {V_{ij}^s\left( {x,\theta } \right)r_{ij}^s\left( t \right) = V_s^T\left( {x,\theta } \right){r^s}\left( t \right),} } } \\ {{v^c} = \sum\limits_{i = 0}^\infty {\sum\limits_{j = 0}^\infty {U_{ij}^c\left( {x,\theta } \right)p_{ij}^c\left( t \right) = U_c^T\left( {x,\theta } \right){p^c}\left( t \right),} } } \\ {{v^c} = \sum\limits_{i = 0}^\infty {\sum\limits_{j = 0}^\infty {V_{ij}^c\left( {x,\theta } \right)r_{ij}^c\left( t \right) = V_c^T\left( {x,\theta } \right){r^c}\left( t \right),} } } \\ {w = \sum\limits_{i = 0}^\infty {\sum\limits_{j = 0}^\infty {{W_{ij}}\left( {x,\nu } \right){s_{ij}}\left( t \right) = {W^T}\left( {x,\theta } \right)s\left( t \right).} } } \end{array}} \right.$ | (12) |
将式(1)、(3)、(8)和(12)带入式(11)可得由模态函数表示的系统动能为
| $\begin{gathered} T = \frac{1}{2}\frac{{d{{({p^s})}^T}}}{{dt}}{M_1}\frac{{d{p^s}}}{{d{p^s}}}dt + \frac{1}{2}\frac{{d({r^s})}}{{d{t^T}}}{M_2}\frac{{d{r^s}}}{{dt}} + \hfill \\ \frac{1}{2}\frac{{d{s^T}}}{{dt}}{M_3}\frac{{ds}}{{dt}} + \frac{1}{2}\frac{{d{{({p^c})}^T}}}{{dt}}{M_4}\frac{{d{p^c}}}{{dt}} + \frac{1}{2}\frac{{d{{({r^c})}^T}}}{{dt}}{M_5}\frac{{d{r^c}}}{{dt}}. \hfill \\ \end{gathered} $ | (13) |
式中:Mi为质量阵中主对角线各元素,质量阵M是对角矩阵.
同理,将式(1)、(2)、(7)和(12)带入式(10)可得由模态函数表示的系统变形能和耗散能之和为
| $\begin{gathered} W = \frac{1}{2}{({p^s})^T}{K_{11}}{p^s} + \frac{1}{2}{({p^s})^T}{K_{12}}{r^s} + \hfill \\ \frac{1}{2}{({p^s})^T}{K_{13}}s + \frac{1}{2}{({p^s})^T}{K_{14}}{p^c} + \frac{1}{2}{({p^s})^T}{K_{15}}{r^c} + \hfill \\ \frac{1}{2}{({r^s})^T}{K_{21}}{p^s} + \frac{1}{2}{({r^s})^T}{K_{22}}{r^s} + \frac{1}{2}{({r^s})^T}{K_{23}}s + \hfill \\ \frac{1}{2}{({r^s})^T}{K_{24}}{p^c} + \frac{1}{2}{({r^s})^T}{K_{25}}{r^c} + \frac{1}{2}{s^T}{K_{31}}{p^s} + \hfill \\ \frac{1}{2}{s^T}{K_{32}}{r^s} + \frac{1}{2}{s^T}{K_{33}}s + \frac{1}{2}{s^T}{K_{34}}{p^c} + \frac{1}{2}{s^T}{K_{35}}{r^c} + \hfill \\ \frac{1}{2}{({p^c})^T}{K_{41}}{p^s} + \frac{1}{2}{({p^c})^T}{K_{42}}{r^s} + \frac{1}{2}{({p^c})^T}{K_{43}}s + \hfill \\ \frac{1}{2}{({p^c})^T}{K_{44}}{p^c} + \frac{1}{2}{({p^c})^T}{K_{45}}{r^c} + \frac{1}{2}{({r^c})^T}{K_{51}}{p^s} + \hfill \\ \frac{1}{2}{({r^c})^T}{K_{52}}{r^s} + \frac{1}{2}{({r^c})^T}{K_{53}}s + \frac{1}{2}{({r^c})^T}{K_{54}}{p^c} + \frac{1}{2}{({r^c})^T}{K_{55}}{r^c}. \hfill \\ \end{gathered} $ | (14) |
式中Kij为刚度阵中各元素,刚度阵K是对称矩阵.
假设圆柱壳一端受集中力q,将q沿坐标x、θ、z方向可以分解为q1、 q2、 q3,则根据虚功原理外力q所做的虚功为
| $\delta {W_2} = {q_1}\delta {u^s} + {q_2}\delta {v^s} + {q_3}\delta w$ | (15) |
将式(12)带入式(15)得由模态函数表示的外力虚功为
| $\delta {W_2} = {Q_{p1}}d{p^s} + {Q_{p2}}d{r^s} + {Q_{p3}}ds.$ | (16) |
哈密顿原理可以表示为
| $\int_{{t_2}}^{{t_1}} {\delta \left( {T - U} \right)dt + \int_{{t_2}}^{{t_1}} {\delta {W_{v1}} + \delta {W_2}dt = 0} } .$ | (17) |
将式(7)、(9)、(10)带入式(17)得
| $\int_{{t_1}}^{{t_1}} {\delta \left( {T - W} \right)dt + } \int_{{t_2}}^{{t_1}} {\delta {W_2}dt = 0} .$ | (18) |
将式(13)、(14)和(16)带入式(18)整理得
| $\left\{ {\begin{array}{*{20}{l}} \begin{gathered} {M_1}\frac{{{d^2}{p^s}}}{{dt}} + {K_{11}}{p^s} + {K_{12}}{r^s} + {K_{13}}s + {K_{14}}{p^c} + \hfill \\ {K_{15}}{r^c} = {Q_{p1}}, \hfill \\ \end{gathered} \\ \begin{gathered} {M_2}\frac{{{d^2}{r^s}}}{{d{t^2}}} + {K_{21}}{p^s} + {K_{22}}{r^s} + {K_{23}}s + {K_{24}}{p^c} + \hfill \\ {K_{25}}{r^c} = {Q_{p2}}, \hfill \\ \end{gathered} \\ {{M_3}\frac{{{d^2}s}}{{{d^2}s}} + {K_{31}}{p^s} + {K_{32}}{r^s} + {K_{33}}s + {K_{34}}{p^c} + } \\ \begin{gathered} {K_{35}}{r^c} = {Q_{p3}}, \hfill \\ {M_4}\frac{{{d^2}{p^c}}}{{dt}} + {K_{41}}{p^s} + {K_{42}}{r^s} + {K_{43}}s + {K_{44}}{p^c} + \hfill \\ {K_{45}}{r^c} = 0, \hfill \\ {M_5}\frac{{{d^2}{p^c}}}{{dt}} + {K_{51}}{p^s} + {K_{52}}{r^s} + {K_{53}}s + {K_{54}}{p^c} + \hfill \\ \end{gathered} \\ {{K_{55}}{r^c} = 0.} \end{array}} \right.$ | (19) |
令Y=[ps,rs,s,pc,rc]T,式(19)可以表示为
| $M({d^2}Y/d{t^2}) + KY = {Q_p}.$ | (20) |
式中M、K、Qp分别表示质量阵、刚度阵和外力矢.
3 振动特性分析 3.1 固有频率和损耗因子敷设约束阻尼圆柱壳的自由振动的动力学方程是式(20)的齐次形式
| $M({d^2}Y/d{t^2}) + KY = {Q_p}.$ | (21) |
令Y(t)=Y0eiωt,其中Y0=[ABCDE]T为振动的振幅,ω为频率,带入式(21)得
| $(K - {\omega ^2}M){Y_0} = 0.$ | (22) |
根据式(22)把求解频率ω的问题转化为求解矩阵特征值,因为黏弹性阻尼具有复常剪切模量,根据式(22)求解的频率表达式为ω2=ω02(1+iη). 特征值的实部表示振动的传播,虚部表示振动的衰减,所以ω的实部表示固有频率,η为该频率下对应的损耗因子.
3.2 频率响应特性圆柱壳上一点受集中载荷q作用,其大小为q(t)=$\bar q$·δ(x-x*)·δ(θ-θ*)eiωt,其中x*、θ*表示作用点的位置. 当敷设约束阻尼圆柱壳以某一阶频率ω振动时,对应的轴向半波数和周向波数为(i,j),此时振幅
| ${Y_{0ij}} = {A_{ij}}{B_{ij}}{C_{ij}}{D_{ij}}E_{ij}^T = {[K - {\omega ^2}M]^{ - 1}}{Q_p}.$ |
应用模态叠加法即可以求出圆柱壳中面位移沿u、v、w方向的位移响应为
| $\left\{ {\begin{array}{*{20}{c}} {{U^s} = \sum\limits_{i = 0}^m {\sum\limits_{j = 0}^n {{A_{ij}}U_{ij}^s(x - {x^*},\theta - {\theta ^*}),} } } \\ {{V^s} = \sum\limits_{i = 0}^m {\sum\limits_{j = 0}^n {{B_{ij}}V_{ij}^s(x - {x^*},\theta - {\theta ^*}),} } } \\ {W = \sum\limits_{i = 0}^m {\sum\limits_{j = 0}^n {{C_{ij}}{W_{ij}}(x - {x^*},\theta - {\theta ^*}).} } } \end{array}} \right.$ |
式中m、n为模态叠加法截取的轴向半波数和周向波数.
4 阻尼评价标准当约束阻尼结构各参数改变时,阻尼效果是不同的. 其中对于阻尼效果影响较大的参数有阻尼材料的阻尼系数g、约束层弹性模量Ec、阻尼层厚度hv、约束层厚度hc. 为了表示方便,将各个参数进行量纲一化. 为此引入约束层弹性模量系数Ec*、阻尼层厚度系数hv*、约束层厚度系数hc*. 各系数分别为:Ec*=Ec/Es,hv*=hv/hs,hc*=hc/hs.
目前,对约束阻尼结构阻尼效果的评价标准大多是在固有频率基础上得到的模态损耗因子. 但是损耗因子只能评价固有频率处的阻尼效果,无法分析在一定频率范围内阻尼的作用. 本节引出一种新的阻尼效果评价标准——能量耗散系数P*,其表达式为
| ${P^*} = 20log({P_{CLD}}/P).$ |
式中:Ps是指圆柱壳位移在指定频带内的平均值,PCLD是指敷设约束阻尼圆柱壳位移在指定频带内的平均值. 当有阻尼作用时P*是一个负数,无阻尼作用时大小为0. 与特定固有频率下损耗因子不同,能量耗散系数P*用一定频带内能量的损耗来表示约束阻尼的阻尼效果,能够直观的表示出在指定频带内参数的改变对阻尼效果的影响.
本文中Ps的求法与PCLD的求法类似,不同之处在于进行动力学方程计算时,求取Ps仅需带入基层动能和变形能.
5 算例分析 5.1 实例验证为了验证本文方法的正确性,将本文计算结果与文献[14]中的结果进行对比. 文献[14]中的敷设约束阻尼圆柱壳各参数:基层半径Rs=0.1 m,长度L=0.1 m,泊松比μs=μc=0.3,基层、阻尼层和约束层厚度hs=hv=hc=1/3 mm,基层和约束层弹性模量Es=Ec=2.1×1011 Pa,密度ρs=ρc=7 850kg/m3,阻尼层密度ρv=1 340 kg/m3,阻尼层复常剪切模量Gv=(8.528+2.985i) MPa,圆柱壳两端的约束方式为简支. 计算结果如表 1所示. 由表 1可知,本文计算结果与文献[14]计算结果吻合较好,实部和虚部的最大误差不超过1%. 由此可以看出本文结果的有效性.
| 表 1 ω2计算结果的对比 Table 1 Comparison of computation results forω2 |
算例中圆柱壳两端约束方式为简支,敷设约束阻尼圆柱壳各参数:基层半径Rs=0.02 m,长度L=0.7 m,泊松比μs=μc=0.3,基层、阻尼层和约束层厚度hs=hv=hc=0.001 m,基层和约束层弹性模量Es=Ec=2.1×1011 Pa,密度ρs=ρc=7 850 kg/m3,阻尼层密度ρv=1 340 kg/m3,根据文献[11],得阻尼层复变剪切模量经验公式Gv=0.142(ω/2π)0.492·(1+1.46i) MPa. 在作用点(x*,θ*)=(0,π)处沿圆柱壳的轴向作用一幅值大小为1 N的力,响应点的坐标(x,θ)=(0.35,0). 应用模态叠加法截取轴向半波数和周向波数分别为m=0~5,n=0~5. 分析响应点在0~3 000 Hz的频带内的幅频响应.
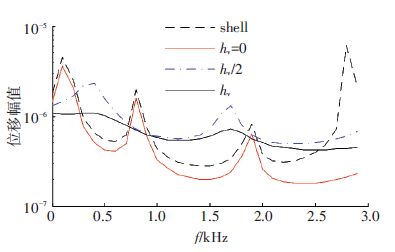
图 3对比在不同阻尼层厚度下圆柱壳响应点的幅频特性,图 3中4条曲线分别表示无约束阻尼作用(shell),阻尼层厚度为0.001 m(hv),阻尼层厚度为0.000 5 m(hv/2)和仅有约束层(hv=0)作用时圆柱壳的响应情况. 由图 3可以看出,在约束阻尼作用下,圆柱壳响应点的幅值明显减少. 减少阻尼层厚度,阻尼效果明显降低. 另外,无约束阻尼作用下圆柱壳频率响应的求法与约束阻尼作用下类似,在求解动能和变形能时只需带入基层的动能和变形能即可.
|
图 3 不同阻尼层厚度圆柱壳响应点的位移幅频特性 Figure 3 Frequency response with CLD treatment of different damping layer thickness |
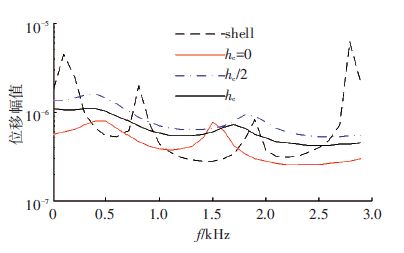
图 4对比在不同约束层厚度下圆柱壳响应点的幅频特性,图 4中4条曲线分别表示无约束阻尼作用(shell),约束层厚度为0.001 m(hc),约束层厚度为0.000 5 m(hc/2)和仅有阻尼层(hc=0)作用时圆柱壳的响应情况. 由图 4可以看出,随着约束层厚度的增加,阻尼效果增强,自由阻尼(hc=0)的阻尼效果比约束阻尼的阻尼效果差.
|
图 4 不同约束层厚度圆柱壳响应点的位移幅频特性 Figure 4 Frequency response with CLD treatment of different constrained layer thickness |
本节对敷设圆柱壳的评价标准是损耗因子和能量耗散系数. 分别用这两种评价标准来表示参数的改变对阻尼效果的影响. 对能量耗散系数分析选取的频率范围是1~2 000 Hz,该频带包含系统的前3阶固有频率. 对应的模态分别为第1阶(i=1,j=1),第2阶(i=2,j=1),第3阶(i=1,j=2).
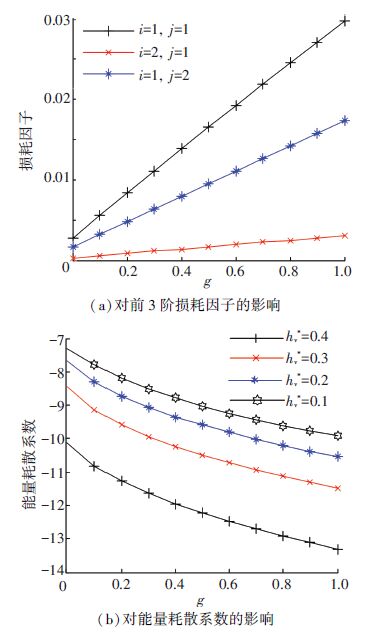
图 5表示阻尼材料的阻尼系数g对阻尼效果的影响,由图 5(a)可以看出,随着系数g的增加,前3阶模态损耗因子增加. 由图 5(b)可以看出在1~2 000 Hz的频带内随着系数g的增加能量耗散系数增加,这说明随着阻尼材料的阻尼系数增加,不仅在前3阶固有频率处阻尼效果增强,在指定的频带内阻尼效果也在增强. 图 6表示约束层弹性模量变化对阻尼效果的影响.
|
图 5 阻尼材料的阻尼系数g对阻尼效果的影响 Figure 5 Influence of damping coefficient g on damping effect |

|
图 6 约束层弹性模量系数Ec*对阻尼效果的影响 Figure 6 Influence of constrained layer elastic modulus coefficient Ec* on damping effect |
当约束层弹性模量Ec在0.01Es~0.5Es之间逐渐增加时,前3阶模态损耗因子急剧下降;但是当约束层弹性模量Ec在0.5Es~Es变化时,前3阶模态损耗因子趋于稳定值. 在1~2 000 Hz的频带范围内,随着约束层弹性模量的增加,能量损耗系数增加. 这说明随着约束层弹性模量的变化,固有频率处的模态损耗因子和系统在指定频带处的阻尼效果的变化是不同的.
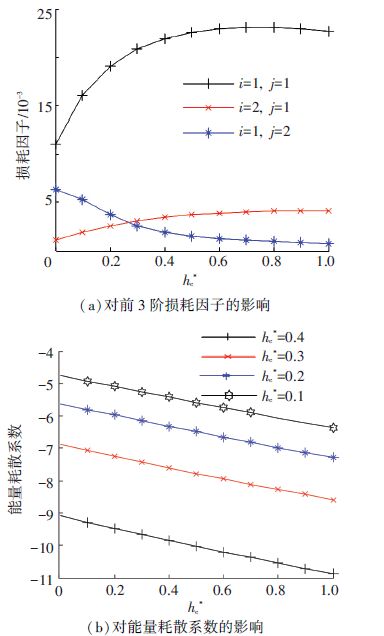
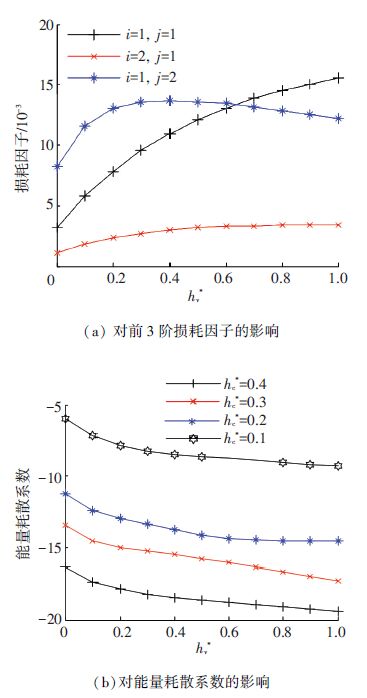
图 7表示约束层厚度对于阻尼效果的影响. 图 7(a)表明,当阻尼层厚度系数hc*在0.01~0.50之间逐渐增加时,第1、第2阶损耗因子增加; 但是,第3阶损耗因子减少. 当hc*在0.50~1.00之间逐渐增加时,前3阶损耗因子趋于稳定值. 图 7(b)表明在1~2 000 Hz的频带内随着约束层厚度的增加,阻尼效果增强. 图 8表示阻尼层厚度变化对阻尼效果的影响. 图 8(a)表明当阻尼层厚度系数hv*增加时,第1、2阶模态损耗因子增加. 随着阻尼层厚度的增加第3阶模态损耗因子先增加后减少. 图 8(b)表明在1~2 000 Hz的频带范围内,随着阻尼层厚度的增加,能量耗散系数先增加最后趋于稳定值,说明在该频带内,随着阻尼层厚度的增加,阻尼效果增强并且存在极限值.
|
图 7 约束层厚度系数hc*对阻尼效果的影响 Figure 7 Influence of constrained layer thickness coefficient hc* on damping effect |
|
图 8 阻尼层厚度系数hv*对阻尼效果的影响 Figure 8 Influence of damping layer thickness coefficient hv* on damping effect |
1) 本文基于薄壳理论,应用哈密顿原理并结合瑞利-李兹法推导出了各种边界条件下敷设约束阻尼圆柱壳的固有频率和损耗因子的计算公式,应用模态叠加法推导了敷设约束阻尼圆柱壳频率响应计算公式.
2) 在频率响应的基础上提出能量耗散系数. 将能量耗散系数和损耗因子分别作为阻尼效果的评价标准对约束阻尼结构进行参数分析.
3) 参数分析结果表明,随着阻尼材料阻尼系数、约束层厚度、约束层弹性模量和阻尼层厚度的改变,前3阶模态损耗因子的变化是不相同的. 但是随着阻尼材料阻尼系数、约束层厚度、约束层弹性模量和阻尼层厚度增加,能量耗散系数增加,在1~2 000 Hz的频带内阻尼效果增强.
4) 能量耗散系数能够作为在指定频带范围内的阻尼效果的评价标准,而损耗因子只能作为在固有频率处阻尼效果的评价标准.
| [1] | LEPOITTEVIN G, KRESS G. Optimization of segmented constrained layer damping with mathematical programming using strain energy analysis and modal data[J]. Materials and Design, 2010, 31 (1) : 14-24. DOI: 10.1016/j.matdes.2009.07.026 |
| [2] | YUAN L, XIANG Y, HUANG Y. A semi-analytical method and the circumferential dominant modal control of circular cylindrical shells with active constrained layer damping treatment[J]. Smart Materials and Structures, 2010, 19 (2) : 1-14. DOI: 10.1088/0964-1726/19/2/025010 |
| [3] | JIN G, YANG C, LIU Z. A unified method for the vibration and damping analysis of constrained layer damping cylindrical shells with arbitrary boundary conditions[J]. Composite Structures, 2015 (130) : 124-142. DOI: 10.1016/j.compstruct.2015.04.017 |
| [4] | MODAMMADI F, SEDAGHATI R. Linear and nonlinear vibration analysis of sandwich cylindrical shell with constrained viscoelastic core layer[J]. International Journal of Mechanical Sciences, 2012, 54 (1) : 156-171. DOI: 10.1016/j.ijmecsci.2011.10.006 |
| [5] | HONGPAN N, YAHONG Z, XINONG Z. Active vibration control of beam using electro-magnetic constrained layer damping[J]. Chinese Journal of Aeronautics, 2008, 21 (2) : 115-124. DOI: 10.1016/S1000-9361(08)60015-1 |
| [6] |
夏峰. 约束阻尼型减振镗杆的研制与开发[D]. 济南:山东大学, 2014:15-20.
XIA Feng. Development of constrained damping boring bar[D]. Jinan: Shandong University, 2014:15-20. http://hkxb.buaa.edu.cn/CN/html/20160629.html |
| [7] | RUZZENE M, BAZ A. Finite element modeling of vibration and sound radiation from fluid-loaded damped shells[J]. Thin-Walled Structures, 2000, 36 (1) : 21-46. DOI: 10.1016/S0263-8231(99)00035-X |
| [8] | WANG H, CHEN L. Finite element dynamic analysis of orthotropic cylindrical shells with a constrained damping layer[J]. Finite Elements in Analysis and Design, 2004, 40 (7) : 737-755. DOI: 10.1016/S0168-874X(03)00112-4 |
| [9] |
王淼, 方之楚. 主动约束层阻尼部分覆盖圆柱壳耦合振动控制[J].
应用力学学报, 2005 (4) : 545-549.
WANG Miao, FANG Zhichu. Coupled vibration control of cylindrical shells partially treated with active constrained layer damping[J]. Chinese Journal of Applied Mechanics, 2005 (4) : 545-549. |
| [10] |
章艺, 童宗鹏, 张志谊. 充液压电阻尼圆柱壳的有限元建模[J].
振动工程学报, 2006, 19 (1) : 24-30.
ZHANG Yi, TONG Zongpeng, ZHANG Zhiyi. Finite element modeling of a fluid-filled cylindrical shell with piezoelectric damping[J]. Journal of Vibration Engineering, 2006, 19 (1) : 24-30. |
| [11] | CHEN L, HUANG S. Vibrations of a cylindrical shell with partially constrained layer damping (CLD) treatment[J]. International Journal of Mechanical Sciences, 1999, 41 (12) : 1485-1498. DOI: 10.1016/S0020-7403(98)00102-7 |
| [12] | HU Y, HUANG S. The frequency response and damping effect of three-layer thin shell with viscoelastic core[J]. Computers and Structures, 2000, 76 (5) : 577-591. DOI: 10.1016/S0045-7949(99)00182-0 |
| [13] | HU Y, HUANG S. A linear theory of three-layer damped sandwich shell vibrations[J]. American Society of Mechanical Engineers, 1996, 93 : 229-234. |
| [14] | XIANG Y, HUANG Y, LU J. New matrix method for analyzing vibration and damping effect of sandwich circular cylindrical shell with viscoelastic core[J]. Applied Mathematics and Mechanics, 2008, 29 (12) : 1587-1600. DOI: 10.1007/s10483-008-1207-x |
| [15] |
向宇, 黄玉盈, 陆静. 部分覆盖PCLD圆柱壳振动分析的新矩阵方法[J].
振动工程学报, 2009 (2) : 175-182.
XIANG Yu, HUANG Yuying, LU Jing. A matrix method for analyzing vibration of a circular cylindrical shell with partially constrained layer damping treatment[J]. Journal of Vibration Engineering, 2009 (2) : 175-182. |
| [16] |
李恩奇, 李道奎, 唐国金, 等. 约束层阻尼圆柱壳动力学分析[J].
工程力学, 2008, 25 (5) : 6-11.
LI Enqi, LI Daokui, TANG Guojin. Dynamic analysis of constrained layed damping cylinderical shell[J]. Engineering Mechanics, 2008, 25 (5) : 6-11. |
| [17] |
翁智远.
圆柱薄壳容器的振动与屈曲[M]. 上海: 上海科学技术出版社, 2007 : 23 -26.
WENG Zhiyuan. Vibration and buckling of cylindrical thin shell vessel[M]. Shang Hai: Shanghai Science and Technology Press, 2007 : 23 -26. |
| [18] | LOY C T, LAM K Y, SHU C. Effects of boundary conditions on frequencies of a multi-layered cylindrical shell[J]. Journal of Sound and Vibration, 1995, 188 (3) : 363-384. DOI: 10.1006/jsvi.1995.0599 |
| [19] |
刘延柱.
振动力学[M]. 北京: 高等教育出版社, 1998 : 130 -133.
LIU Yanzhu. Vibration mechanics[M]. Beijing: Higher Education Press, 1998 : 130 -133. |
 2017, Vol. 49
2017, Vol. 49


