2. 哈尔滨工业大学 电气工程学院, 哈尔滨 150001
2. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
Formula Society of Automotive Engineers (FSAE)由国际汽车工程师学会开办,是面向全世界在校大学生的方程式赛车竞赛,要求所设计制造的赛车在加速、制动、操纵稳定性及耐久性方面都有优秀的表现. FSAE纯电动赛车耐久赛规则为:同样行驶里程情况下,总能量消耗越少,分数越高;而对于配备再生制动功能的电动赛车,所回收的制动能量将按90%从总能量中扣除. 再生制动系统在民用车领域应用较为广泛. 丰田公司的混合动力汽车Prius,基于线控制动方案搭载了再生制动系统[1];本田公司的混合动力汽车Insight应用了双制动力分配系数的再生制动控制策略[2];马自达公司研发的i-eloop再生制动系统则是以电容作为能量存储单元,已应用在量产车型中[3]. 控制策略方面,国内外学者做了大量的研究[4-11],并设计了相关硬件系统,同时还研究了与ABS等相关系统的协调控制算法. Sankavaram等[12]针对带有制动能量回收功能的混合动力汽车,研究了制动能量回收功能的错误监测和诊断系统;Jiweon等[13]设计了具有ABS功能的再生制动协调算法; 赵国柱[14]在制动系统中加入惯性比例阀来提高汽车制动能量回收效果; 曹建波等[15]设计了基于RBF神经网络调节的制动能量回收滑膜控制器,具有更好的响应速度和鲁棒性. 在赛车领域,由于赛车本身尺寸及质量较小,在轻量化及动力匹配方面已基本达到极限,为进一步提高电动赛车的耐久赛成绩,研究适用于FSAE赛车的再生制动系统具有重要意义.
1 FSAE电动赛车FSAE纯电动赛车底盘传动及制动系统如图 1所示. 赛车为后轴驱动,由一台永磁同步电机经链传动将动力传至后轮,选用磷酸铁锂电池作为能量存储单元,制动系统为机械液压结构,以固定比值分配前、后制动力. FSAE电动赛车的主要参数见表 1.

|
图 1 赛车底盘系统 Figure 1 Chassis system schematic of racing |
| 表 1 FSAE电动赛车主要参数 Table 1 Main parameters of FSAE electric car |
本文采用ADVISOR软件进行仿真分析. 原软件仅支持前轴驱动车辆的仿真,为使其适用于后轴驱动FSAE电动赛车,需对软件原有模型进行二次开发,修改的部分主要包括整车模型、车轮模型、驱动控制模块和动力系统模块.
2.1 整车模型整车模型的修改主要考虑赛车的直线行驶工况,忽略转向工况及悬架的影响. 赛车行驶时的动力学方程式为
| $\left\{ {\begin{array}{*{20}{l}} {{F_t} = {F_f} + {F_w} + {F_i} + {F_j},} \\ {{F_f} = mgcos\alpha ({f_1} + {f_2}),} \\ {{F_w} = {C_D}A\rho {u_a}^2/2,} \\ {{F_i} = mgsin\alpha ,} \\ {{F_j} = \delta md{u_a}/dt.} \end{array}} \right.$ | (1) |
式中:Ft为行驶驱动力,Ff为滚动阻力,Fw为空气阻力,Fi为坡度阻力,Fj为加速阻力,m为整车质量,g为重力加速度,f1、f2为前、后轮滚动阻力系数,δ为旋转质量换算系数,α为汽车行驶坡度,ua为赛车行驶车速,CD为空气阻力系数;A为赛车迎风面积,ρ为空气密度.
整车后向模型的输入信号为整车需求车速ua,采用当前步长内的初速度与工况模块传来的速度的平均值,即
| ${u_a} = ({V_{pre}} + {V_{cyc}})/2$ |
式中:Vpre为后向模型中当前步长内初速度,Vcyc为工况模块的速度输入.
整车模型的前向模型根据车轮模块传来的实际牵引力及车速信号,计算下一步长的初始车速Vpre.
| $\left\{ {\begin{array}{*{20}{c}} {d{u_a}/dt = ({V_{pre}} - {V_0})/\Delta t = 2({V_{ave}} - {V_0})/\Delta t,} \\ {{V_{ave}} = ({V_{pre}} + V)/2.} \end{array}} \right.$ | (2) |
式中:V0为前向模型当前步长的初始车速,Vave为当前步长平均车速.
将式(2)带入式(1),可得
| $\begin{gathered} {F_t} - {C_D}A\rho {V_{ave}}^2/2 - mgcos\alpha ({f_1} + {f_2}{V_{ave}}) - \hfill \\ mgsin\alpha - 2\delta m\left( {{V_{ave}} - {V_0}} \right)/\Delta t = 0. \hfill \\ \end{gathered} $ | (3) |
求解式(3)可得Vave,进而求得前向模型中当前步长末速度Vpre.
2.2 车轮模型车轮计算模型主要负责连接整车计算模型与传动系统模型. 其中,车轮后向模型接收赛车行驶驱动力及速度信号,向传动系统提供需求转速及转矩信号;车轮前向模型接收来自传动系统的转矩及转速信号,向整车模型输出实际车速及驱动力信号. 在ADVISOR软件车轮模型中,需要针对驱动形式进行修改的模块包括:滑移率限制模块、惯性损失模块及相应的通信模块.
2.3 驱动控制模块驱动模块位于整车控制模块中,其作用是与车轮模块中的后向模型进行信号通信,限制整车模块向车轮后向模块输出的力信号及车速信号的大小.
后轴最大驱动力限制模块及后轴载荷计算模块的作用是:限制整车模块向车轮模块输出的需求驱动力,使最大驱动力不超过地面附着条件所能提供的最大附着力,保证仿真的精确度. 地面对赛车后轴的法向反力Fz2为
| $\left\{ {\begin{array}{*{20}{c}} {{F_{z2}} = mgcos\alpha \left( {a/L} \right) + mgsin\alpha ({h_g}/L) + ma({h_g}/L),} \\ {a = 2({V_{ave}} - {V_0})/\Delta t.} \end{array}} \right.$ |
此时最大驱动力限制为Fmax=Fz2·φmax.
整车车速限制模块的作用是:接收整车模块的速度输出信号,限制整车速度不能超过最大附着条件下的最大车速,并将速度信号输出至车轮模块中.
假设汽车在坡度角为α的斜坡上以初速度αj,加速度aj加速上坡,经过Δt时间后达到速度Vt,当驱动力Ft与地面最大附着力Fmax相等时,有
| ${F_{max}} - {F_f} - {F_w} - {F_i} - {F_j} = 0.$ |
其中:
| $\left\{ {\begin{array}{*{20}{l}} {{F_{max}} = {F_{z2}}\cdot{\varphi _{max}},} \\ {{F_{z2}} = mgcos\alpha \left( {a/L} \right) + mgsin\alpha ({h_g}/L) + {F_j}({h_g}/L),} \\ {{F_w} = {C_D}A\rho {V^2}_{ave}/2,} \\ {{F_j} = m{a_j},} \\ {{F_f} = mgcos\alpha ({f_1} + {f_2}{V_{ave}}),} \\ {{F_i} = mgsin\alpha .} \end{array}} \right.$ | (4) |
式中:hg为汽车质心高度,L为汽车轴距,a为质心至前轴距离,b为质心距后轴距离,φmax为路面最大附着系数.且又有
| $\left\{ {\begin{array}{*{20}{c}} {{a_j} = ({V_t} - {V_0})/\Delta t,} \\ {{V_{ave}} = ({V_t} + {V_0})/2.} \end{array}} \right.$ | (5) |
联合式(4)与式(5),可以得出驱动工况下,驱动力达到地面最大附着条件时汽车能达到的速度.
2.4 动力系统模块动力系统模块主要包括动力传动系统模型、电机/控制器模型、电器附件模型以及储能单元模型. 采用ADVISOR软件原动力系统相关模型,根据FSAE电动赛车动力系统主要参数修改相应配置文件.
综合以上分析,在ADVISOR中创建后轴驱动FSAE赛车仿真模型,如图 2所示.

|
图 2 后轴驱动FSAE赛车ADVISOR仿真模型 Figure 2 ADVISOR simulation model of the rear axle drive FSAE car |
FSAE纯电动赛车液压制动系统按固定比值分配前、后制动力,在后轴增加电机制动力. 由于车身尺寸及质量较小,制动时所需制动力也较小,并且考虑到赛车在赛道行驶制动时的制动安全性,因而未更改原车液压制动系统的机械结构.
对于前轴驱动的电动汽车,再生制动只能用在前轮. 通常为保证制动稳定性,应使前、后轴制动力分配曲线靠近I曲线,但这样会增加后轴液压制动力,减弱了前轴再生制动力的参与. 而后轴驱动的FSAE电动赛车不存在此种矛盾,因而可以更好地协调制动稳定性和能量回收效果.
受整车控制器和传感器的精度限制,理想制动力分配控制策略、最大再生制动力控制策略在FSAE赛车上并不能完全发挥功效. 因此,考虑动力电池、电机状态及外界负载状态等影响因素,本文提出了一种既能保证制动安全、又能尽量回收制动能量,同时又能稳定运行的后轴并联制动控制策略. 图 3为该策略下前、后轮制动力分配关系曲线.
|
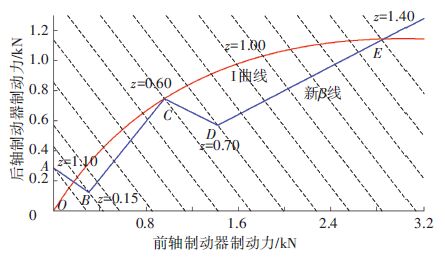
图 3 制动力分配关系曲线 Figure 3 Curve of braking force distribution |
由图 3可知后轴并联再生制动控制策略如下.
1) 制动强度<0.1时,属于小强度制动工况,液压系统不工作(通过增设制动踏板空行程方式实现),整车制动力全部由电机制动力提供;
2) 制动强度在0.10~0.15时,液压制动系统开始工作,后轴液压制动力增加,为保证制动稳定性,电机制动力开始衰减,后轴总制动力随着制动强度的增加而减弱;
3) 制动强度在0.15~0.60时,属于中等强度制动工况,此时电机制动力随着制动强度的增加而增大,后轴制动力占总制动力份额上升,前、后轮制动力关系曲线向I曲线贴近,但仍低于I曲线;
4) 制动强度在0.60~0.70时,属于由中等强度制动工况向大制动强度制动工况过度阶段,此时,原车液压制动系统制动力仍在上升,而减小电机制动力,当制动强度达到0.7时,电机制动力减小至0;
5) 当制动强度>0.70时,制动强度大,属于紧急制动工况. 为保证赛车制动安全,撤销电机制动力,改为液压制动系统工作. 此时整车前、后车轮制动力分配曲线回归原车实际液压制动力分配曲线(β线).
所采用的磷酸铁锂电池组SOC的工作范围为5%~95%,因此当电池SOC低于95%时,开启再生制动功能. 另外,FSAE比赛规定:对于装有再生制动功能的赛车,当速度低于5 km/h时,不可进行再生制动,因此策略中系统运行的最低车速为5 km/h.
4 再生制动系统控制器设计 4.1 硬件设计核心控制芯片选用意法半导体(ST)公司所生产的32位微控制器STM32F105RBT6,其最小系统电路包括电源电路、时钟电路、复位电路. 采用线性稳压电源,将车内12 V电压转换为中间值的7 V电压,再分别转换为5 V及3.3 V的芯片工作电压. 时钟电路是通过在芯片外部接口OSC_IN/PD0和OSC_OUT/PD1上接入频率为8 MHz的晶振,利用芯片的内部锁相环,将频率提高到芯片运行频率72 MHz来驱动芯片正常运行.
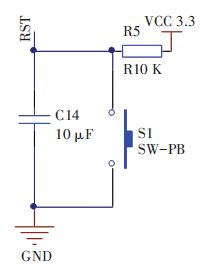
STM32F105RBT6芯片本身集成有一个内部上电复位电路和一个内部掉电复位电路,但是在控制器硬件及软件设计完成进行调试时,无法经常通过电源的通断来进行复位. 因此,为了方便硬件调试过程,设计了外置手动RC复位电路,见图 4.
|
图 4 外置RC复位电路 Figure 4 External RC reset circuit |
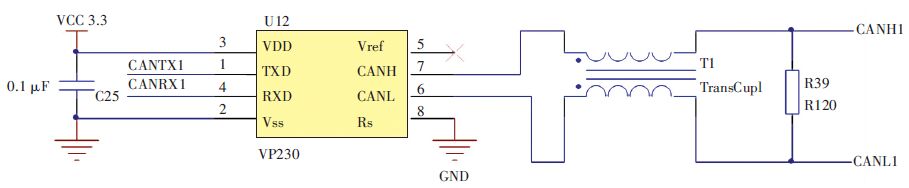
控制器CAN总线通信电路如图 5所示,采用VP230作为报文收发芯片,采用3.3 V电压供电.
|
图 5 CAN通信接口电路 Figure 5 CAN communication interface circuit |
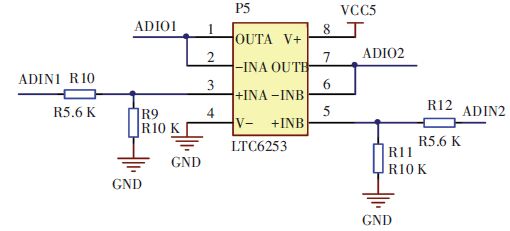
A/D输入信号调理电路见图 6. 采用LTC6253芯片,传感器信号经分压电路转换为3.3 V电压,经过电压跟随器进行阻抗匹配,进入STM32F105RBT6芯片内进行A/D转换. 考虑到传感器信号的扩展性,共设计5路信号调理电路,其原理相同.
|
图 6 A/D输入信号调理电路 Figure 6 A/Dinput signal conditioning circu |
输入信号保护电路用于防止高压冲击等危险情况对核心控制芯片造成损坏,本文采用PS2501L-1光耦原件,输入、输出端进行完全地电气隔离,如图 7所示.

|
图 7 输入保护电路 Figure 7 Input protection circuit |
系统软件开发使用的是美国Keil Software公司所开发的c语言开发环境Keil μVision4. 采用模块化设计方法,进行了软件系统初始化配置设计、针对传感器信号采集及转换的A/D信号处理设计、再生制动控制策略主程序设计、CAN通信软件设计和串口通信软件设计等.
5 仿真分析及实车试验对提出的控制策略进行软件仿真. 行驶工况模型采用原ADVISOR软件自带模型,将耐久赛工况数据写入相对应的.mat文件中,并对配置m文件进行修改.
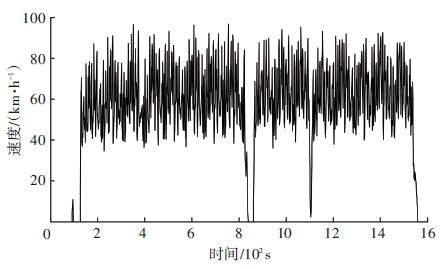
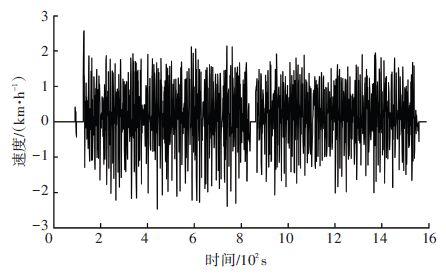
图 8为修改后的耐久赛行驶工况,图 9为该工况下赛车需求驱动力及制动力变化曲线. 分析图 9、10可知,仿真过程中赛车的车速变化频繁,制动工况占有很大比例. 实际比赛中,赛道的急弯较多且专门设置了大量障碍物,赛车需要不断加减速,因而再生制动功能可以充分发挥作用.
|
图 8 耐久赛工况 Figure 8 Endurance race working conditions |
|
图 9 耐久赛整车需求驱动力-制动力曲线 Figure 9 Endurance race vehicle demand driving force- braking force curve |
|
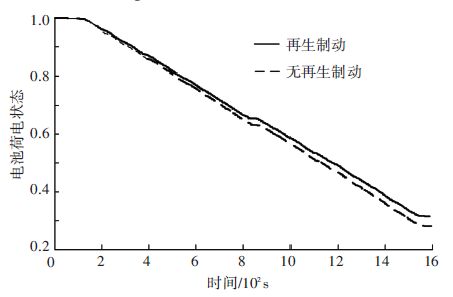
图 10 有/无再生制动时电池SOC对比曲线 Figure 10 Comparison of the SOC of the battery with / without regenerative braking |
用能量回收率ηreg衡量再生制动系统的表现,且令
| ${\eta _{reg}} = \frac{{{E_{reg}}}}{{{E_{brake}}}} \times 100\% .$ | (6) |
式中:Ereg为回收到蓄电池中的能量,Ebrake为制动过程耗总能量,其表达式分别为
| ${E_{reg}} = \smallint UIdt,$ | (7) |
| $\begin{gathered} {E_{brake}} = \frac{1}{2}m{u_a}^2 - \int {mg\left( {{f_1} + {f_2}} \right){u_a}dt} - \hfill \\ \int {{C_D} \cdot A/21.15 \cdot {{\left( {3.6} \right)}^2} \cdot {u_a}dt.} \hfill \\ \end{gathered} $ | (8) |
式中:U为电池组输出电压,I为电池充电电流.
图 10为有/无再生制动时电池的SOC曲线对比图. 由图 10可见,耐久赛后电池SOC值下降明显,所提出的后轴并联再生制动控制策略改善了动力电池的SOC曲线,可有效回收制动能量,提高比赛成绩.
表 2为ADVISOR软件仿真耐久赛工况得出的赛车能量数据. 在耐久赛工况下,后轴并联再生制动控制策略的制动能量回收率为20.89%,根据前文所述FSAE耐久赛规则,可将成绩提高7.19%.
| 表 2 能量利用仿真数值 Table 2 Numerical simulation of energy utilization |
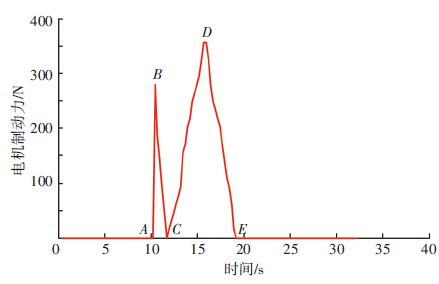
首先设计试验检测再生制动硬件系统运行状况. 赛车以初速度60 km/h进行直线减速至停车,图 11为该制动过程中实际电机制动力输出结果. A点之前为纯电机制动,通过设置额外踏板空行程实现;A点为液压制动力开始介入的起始点,电机制动力随踏板开度增加而下降至零;BC为中等强度制动,电机制动力随踏板开度增加开始逐渐上升,与液压制动力并联制动;CD段进入大制动强度阶段,电机制动力减小至零;D点后制动强度较大,为保证制动安全性,电机制动退出,由液压制动系统将车停住.
|
图 11 实际电机制动力 Figure 11 Practical motor braking force |
由于FSAE纯电动赛车制动踏板位移较小,制动系统响应灵敏,且传感器精度、采样频率以及踩踏制动踏板的速度并不能保证完全匀速,所输出的电机制动力曲线并不完全呈线性变化,但系统仍能按照所设计的控制策略运行.
随后按照耐久赛要求布置场地,并使赛车电池SOC 初始值高于95%,将后轴并联控制策略写入控制器,进行实车试验. 将数据采集器中的电池充放电电压和电流数据导出,根据式(6)~(8)计算出实车试验时赛车的能量利用结果(见表 3). 后轴并联控制策略的能量回收率为19.07%,按照FSAE耐久赛规则,成绩提高了7%.
| 表 3 能量利用试验数据 Table 3 Energy utilization test data sheet |
对比仿真与实车试验,能量回收率的误差约为8.7%,实车试验时的能量回收率较低. 主要原因是试验所用的练习赛道与实际耐久赛的赛道相比,弯道及障碍物所占比例相对较少,因而制动工况少. 同时在仿真中未考虑控制器、传感器和数据采集器的精度对实际结果的影响,由硬件精度造成的误差使实车试验中的能量回收率降低.
6 结 论1) 后轴并联再生制动控制策略充分考虑了FSAE纯电动赛车体积小、质量轻的特点,同时兼顾控制器与传感器精度、电机电池特性和制动工况特性,较好地兼容了制动稳定性和能量回收效果,仿真和试车试验中的能量回收率分别为20.89%和19.07%.
2) 设计开发了整车控制器. 实车试验结果证明,控制器可稳定工作,所提出的再生制动控制策略可有效运用于后轴驱动FSAE赛车.
3) 受硬件系统精度及项目时间限制,本文采用了易于实现的并联控制策略,未能探讨理想制动控制和最大再生制动控制策略在FSAE赛车上的可行性,后续可对此进行深入研究.
| [1] | DUOBA M, BOHN T, LOHSE-BUSCH H. Investigating possible fuel economy bias due to regenerative braking in testing HEVs on 2WD and 4WD chassis dynamometers[J]. SAE transactions, 2005, 114 (4) : 324-334. DOI: 10.4271/2005-01-0685 |
| [2] |
李贺.纯电动汽车的再生制动系统与ABS集成控制策略研究[D].武汉:武汉理工大学,2012. DOI:10.7666/d.y2099088.
LI He. A study on regenerative of braking system of pure[D]. Wuhan: Wuhan University of Technology, 2012. DOI:10.7666/d.y2099088 |
| [3] | WIESBADEN S F. Mazda’s i-ELOOP: saves engine power, boosts fuel efficiency[J]. Auto Tech Review, 2013, 2 (2) : 64-64. DOI: 10.1365/s40112-013-0236-8 |
| [4] | EHSANI M, GAO Yimin, MILLER J M. Hybrid electric vehicles: architecture and motor drives[J]. Proceedings of the IEEE, 2007, 95 (4) : 719-728. DOI: 10.1109/JPROC.2007.892492 |
| [5] |
仇斌.电动城市公交车制动能量回收过程中的能量效率研究[D].北京:清华大学, 2011.
QIU Bin. Research on the energy efficiency of electric city bus during regenerative braking[D]. Beijing: Tsinghua University, 2011. http://cn.bing.com/academic/profile?id=e92c2046f50537e9f3daf80366b94330&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | SANGTARASH F, ESFAHANIAN V, NEHZATI H, et al. Effect of different regenerative braking strategies on braking performance and fuel economy in a hybrid electric bus employing CRUISE vehicle simulation[J]. SAE International Journal of Fuels and Lubricants, 2009, 1 (1) : 828-837. DOI: 10.4271/2008-01-1561 |
| [7] | AHN J K, JUNG K H, KIM D H, et al. Analysis of a regenerative braking system for hybrid electric vehicles using an electro-mechanical brake[J]. International Journal of Automotive Technology, 2009, 10 (2) : 229-234. DOI: 10.1007/s12239-009-0027-z |
| [8] | PENG Dong, ZHANG Y, YIN Chengliang, et al. Combined control of a regenerative braking and antilock braking system for hybrid electric vehicles[J]. International Journal of Automotive Technology, 2008, 9 (6) : 749-757. DOI: 10.1109/STUDENT.2010.5686984 |
| [9] | OLEKSOWICZ S A, BURNHAM K J, BARBER P, et al. Investigation of regenerative and anti-lock braking interaction[J]. International Journal of Automotive Technology, 2013, 14 (4) : 641-650. DOI: 10.1007/s12239-013-0069-0 |
| [10] | YANG M J, JHOU H L, MA B Y, et al. A cost-effective method of electric brake with energy regeneration for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (6) : 2203-2212. DOI: 10.1109/TIE.2009.2015356 |
| [11] | SEKI H, ISHIHARA K, TADAKUMA S. Novel regenerative braking control of electric power-assisted wheelchair for safety downhill road driving[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (5) : 1393-1400. DOI: 10.1109/TIE.2009.2014747 |
| [12] | SANKAVARAM C, PATTIPATI B, PATTIPATI K R, et al. Fault diagnosis in hybrid electric vehicle regenerative braking system[J]. IEEE Access, 2014, 2 : 1225-1239. DOI: 10.1109/ACCESS.2014.2362756 |
| [13] | JIWEON K, KO S, SON H, et al. Development of brake system and regenerative braking cooperative control algorithm for automatic-transmission-based hybrid electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2015, 64 (2) : 431-440. DOI: 10.1109/TVT.2014.2325056 |
| [14] |
赵国柱.电动汽车再生制动若干关键问题研究[D].南京:南京航空航天大学, 2012.
ZHAO Guozhu. Research on key problems of regenerative braking for electric vehicles[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. http://cn.bing.com/academic/profile?id=f1023aad9a2bc18f518d349e36418702&encoded=0&v=paper_preview&mkt=zh-cn |
| [15] |
曹建波, 曹秉刚, 王军平, 等. 基于RBF神经网络调节的电动车驱动和再生制动滑模控制[J].
吉林大学学报(工学版), 2009, 39 (4) : 1019-1024.
CAO Jianbo, CAO Binggang, WANG Junping, et al. Sliding mode control for driving and regenerative braking of electric vehicle based on RBF neural network[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39 (4) : 1019-1024. DOI: 10.13229/j.cnki.jdxbgxb2009.04.048 |
 2017, Vol. 49
2017, Vol. 49


