坐标旋转数字计算机(Coordinate Rotation Digital Computer，CORDIC)是J.Volder于1959年提出的一种算法^[1]，这种算法通过一系列旋转角不断逼近目标角度，由移位相加迭代得到目标角度的正余弦值^[2]. CORDIC算法具有硬件实现简单、速度快、精度可调等优点，在全数字锁相环、直接数字频率合成、快速傅里叶变换等领域有着广泛应用^[3-6].传统的CORDIC算法采用流水线型结构^[7]，通过大量迭代来保证输出精度，因此存在硬件资源消耗过多、输出时延较长的问题.

随着现代数字通信系统集成化程度和精度的不断提高，许多学者对CORDIC算法提出改进方案.文献[8]提出一种贪婪搜索算法，采用跳过若干旋转角度和重复某些旋转角度的方法进行迭代，迭代次数有一定减少，但硬件复杂度明显增加.文献[9]采用一种混合结构，将旋转角度分为两部分处理，与传统流水线型CORDIC算法相比提高运算速度，但仍存在硬件消耗大、输出精度低的问题.文献[10]中的免缩放因子双步旋转算法免去缩放因子，减少迭代次数，但双步旋转的硬件实现结构较为复杂.文献[11]提出免缩放自适应CORDIC算法，虽然硬件资源消耗和误差有所减少，但是计算所需的时钟周期太长.文献[12-13]提出一种三阶段CORDIC算法，第一阶段通过查找表得到若干次迭代后的值，第二阶段采用移位相加的蝶形迭代运算，第三阶段进行合并迭代，相比于传统的流水线型CORDIC算法在精度和硬件消耗上都有一定改善，计算所需的周期少，具有一定代表性和优越性.

本文在文献[12-13]的基础上结合角度二极化重编码(Binary To Bipolar Recoding, BBR)、角度区间折叠、合并迭代等手段提出一种免查找表CORDIC算法，将三阶段缩减为两阶段实现.在典型的三阶段CORDIC实现方法基础上，将第一阶段的查找表直接替换为有限的几步移位相加迭代运算，有效减少寄存器消耗.此外，将第二阶段和第三阶段合并为一步迭代，大幅减少输出时延.用几步迭代运算代替查找表，使输出延时有所增加，但第二阶段的合并迭代只需要一个时钟周期，同时省去原有的蝶形运算阶段，整体只需要5个时钟周期就能得到输出结果，整体延时还有所降低.同时在综合采用角度二极化重编码和角度区间折叠技术后，改进算法的精度相比于传统实现方法也有一定改善.

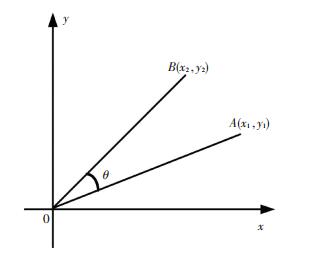
1 CORDIC算法基本原理

CORDIC算法通过一系列旋转角不断逼近输入角度，由移位相加迭代得到输入角度的正余弦值. 图 1为向量旋转图，在平面直角坐标系中将初始向量OA=(x₁, y₁)逆时针旋转角度θ到向量OB=(x₂, y₂)，则坐标之间的关系为

$ \begin{array}{l} \left[\begin{array}{l} {x_2}\\ {y_2} \end{array} \right] = \left[\begin{array}{l} \cos \theta \;\;\;\;\;\;-\sin \theta \\ \sin \theta \;\;\;\;\;\;\;\;cos\theta \end{array} \right] = \\ \cos \theta \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;-\tan \theta \\ \tan \theta \;\;\;\;\;\;\;\;\;1 \end{array} \right]\left[\begin{array}{l} {x_1}\\ {y_1} \end{array} \right]. \end{array} $

(1)

将角度θ视为N个角度的累加和，即$\theta = \sum\limits_{i = 0}^{N-1} {{\delta _i}{\theta _i}} $，其中δ_i=±1，那么式(1)可写为

$ \begin{array}{l} \left[\begin{array}{l} {x_2}\\ {y_2} \end{array} \right] = \cos {\theta _{N - 1}}\cos {\theta _{N - 2}} \cdots \cos {\theta _0} \cdot \\ \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-\tan {\delta _{N-1}}{\theta _{N-1}}\\ \tan {\delta _{N - 1}}{\theta _{N - 1}}\;\;\;\;\;\;\;\;\;\;1 \end{array} \right]\\ \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-\tan {\delta _{N-2}}{\theta _{N-2}}\\ \tan {\delta _{N - 2}}{\theta _{N - 2}}\;\;\;\;\;\;\;\;\;\;\;1 \end{array} \right] \cdots \cdot \\ \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;-\tan {\delta _0}{\theta _0}\\ \tan {\delta _0}{\theta _0}\;\;\;\;\;\;1 \end{array} \right]\left[\begin{array}{l} {x_1}\\ {y_1} \end{array} \right] = \\ K \cdot \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;-\tan {\delta _{N-1}}{\theta _{N-1}}\\ \tan {\delta _{N - 1}}{\theta _{N - 1}}\;\;\;\;\;\;\;\;1 \end{array} \right] \cdot \\ \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;-\tan {\delta _{N-2}}{\theta _{N-2}}\\ \tan {\delta _{N - 2}}{\theta _{N - 2}}\;\;\;\;\;\;\;\;1 \end{array} \right] \cdots \\ \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;-\tan {\delta _0}{\theta _0}\\ \tan {\delta _0}{\theta _0}\;\;\;\;\;\;1 \end{array} \right]\left[\begin{array}{l} {x_1}\\ {y_1} \end{array} \right] \end{array} $

(2)

其中:K=cos θ_N－1cos θ_N－2…cos θ₀称为校模因子，在N确定时可视为常数.令θ_i=arctan(2^－i)，在单次迭代时不考虑校模因子，那么有$\left[\begin{array}{l} {x_{i + 1}}\\ {y_{i + 1}} \end{array} \right] = \left[\begin{array}{l} 1\;\;\;\;\;\;\;\;-{\delta _i}{2^{-i}}\\ {\delta _i}{2^{-i}}\;\;\;\;\;\;1 \end{array} \right]\left[\begin{array}{l} {x_i}\\ {y_i} \end{array} \right] $.从上式可以看出，CORDIC算法只需要移位和加减操作就能完成正余弦的计算.为判断每次旋转的方向，引入变量Z，令${Z_{N + 1}} = \theta-\sum\limits_{i = 0}^N {{\theta _i}} $，其取值非负时δ_i=+1，取值为负数时δ_i=-1.

2 免查找表CORDIC算法 2.1 角度二极化重编码

对于取值为[0, π/8]的任意输入角度θ可用N位二进制小数示为$\theta = \sum\limits_{k = 2}^N {{b_k}{2^{-k}}} $，其中b_k∈(0, 1).假设r_k=2b_k－1，那么有$\theta = \sum\limits_{k = 3}^N {{2^{-k}}} + \sum\limits_{k = 3}^{N + 1} {{r_k}{2^{-k}}} = {\varphi _0} + \sum\limits_{k = 3}^{N + 1} {{r_k}{2^{-k}}} $，其中${\varphi _0} = \sum\limits_{k = 3}^{N + 1} {{2^{-k}}} = \frac{1}{4}-{\left( {\frac{1}{2}} \right)^{N + 1}} $，这种方法称为角度二极化重编码^[4].初始向量为(x₀, y₀)=(K, 0)，在得到输入角度后，先将初始向量逆时针旋转角度φ₀，随后根据二进制角度的比特位值进行旋转.当b_k=1时r_k=1，将向量逆时针方向旋转2^-k弧度；当b_k=0时r_k=-1，将向量顺时针方向旋转2^-k弧度.

2.2 免查找表与合并迭代原理

根据CORDIC算法的基本原理，可通过式(3)迭代得到输入角度的正余弦值

$ \left\{ \begin{array}{l} {x_{k + 1}} = {x_k}-{r_k}\tan \left( {{2^{-k}}} \right){y_k}, \\ {y_{k + 1}} = {y_k} + {r_k}\tan \left( {{2^{-k}}} \right){x_k}. \end{array} \right. $

(3)

式中k代表迭代次数.

在三阶段CORDIC算法中，对于输出N位的CORDIC算法，当k < N/3时可利用上式(3)建立第一阶段的小容量查找表.当N/3≤k < N/2时，利用tan(2^－k)≈2^－k进行第二阶段的蝶形运算，当k≥N/2时进行合并迭代.本文提出的免查找表CORDIC改进算法将第一阶段中tan(2^－k)用二进制小数近似，对于输出为16位小数的CORDIC算法，第一阶段用到的近似如式(4)所示.

$ \left\{ \begin{array}{l} \tan \frac{1}{8} \approx {2^{-3}} + {2^{-11}} + {2^{-13}} + {2^{ - 15}} + {2^{ - 17}}, \\ \tan \frac{1}{{16}} \approx {2^{ - 4}} + {2^{ - 14}} + {2^{ - 16}}, \\ \tan \frac{1}{{32}} \approx {2^{ - 5}} + {2^{ - 17}}, \\ \tan \frac{1}{{64}} \approx {2^{ - 6}}. \end{array} \right. $

(4)

那么式(3)中乘以正切项就可视为移位相加运算，其中k=3对应的结构见图 2.

图 2中(a)和(b)分别代表式(3)中的两个子式.通过这种近似方法，将查找表替换为移位相加的蝶形运算结构，从而减少寄存器消耗.

对于输出为N位小数的CORDIC算法，当迭代次数k≥N/2时，可作tan(2^－k)≈2^－k的近似，那么上式(3)所示的迭代可写为$\left\{ \begin{array}{l} {x_{k + 1}} = {x_k}-{r_k}{2^{-k}}{y_k}\\ {y_{k + 1}} = {y_k} + {r_k}{2^{-k}}{x_k} \end{array} \right. $，所以迭代次数k>N/2后的s次蝶形运算可简化为$\left\{ \begin{array}{l} {x_{k + s}} = {x_k}-{y_k} \cdot \sum\limits_{i = k}^{k + s-1} {{r_i}{2^{-i}}} \\ {y_{k + s}} = {y_k} + {x_k} \cdot \sum\limits_{i = k}^{k + s - 1} {{r_i}{2^{ - i}}} \end{array} \right. $，在硬件实现时相当于移位连加结构.

2.3 区间角度折叠及映射关系

对于(π/8, π/4]内的角度，存在式(5)所示的三角函数关系式

$ \left\{ \begin{array}{l} \sin \left( {\frac{\pi }{4}-\theta } \right) = \frac{{\sqrt 2 }}{2}\left( {\cos \theta-\sin \theta } \right), \\ \cos \left( {\frac{\pi }{4}-\theta } \right) = \frac{{\sqrt 2 }}{2}\left( {\cos \theta + \sin \theta } \right). \end{array} \right. $

(5)

通过上式(5)可将(π/8, π/4]内的角度折叠到[0, π/8]内，有

$ \left\{ \begin{array}{l} \cos \theta = \frac{{\sqrt 2 }}{2}\left[{\cos \left( {\frac{\pi }{4}-\theta } \right) + \sin \left( {\frac{\pi }{4}-\theta } \right)} \right], \\ \sin \theta = \frac{{\sqrt 2 }}{2}\left[{\cos \left( {\frac{\pi }{4}-\theta } \right)-\sin \left( {\frac{\pi }{4}-\theta } \right)} \right]. \end{array} \right. $

(6)

从式(6)看出，只要得到[0, π/8]内角度的正余弦值，进行一次加减法运算和$ \sqrt 2 /2$缩放就可得到(π/8, π/4]内的正余弦值.通过类似的三角函数关系式，可将角度扩展到[0, 2π]范围内. 表 1是具体的角度映射和正余弦转换关系，其中θ′是输入角度经过区间角度折叠预处理后所得到的角度.

将角度折叠到[0, π/8]可以省掉三阶段算法中第二阶段的蝶形运算过程，只需要进行第一阶段的移位相加迭代和第三阶段的合并迭代，随后根据角度映射和转换关系即可还原输出正余弦值.

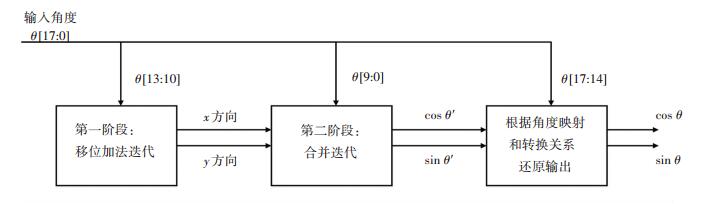
3 算法实现

对于三阶段算法，第一阶段是建立小容量查找表，将经过校模因子缩放后的横纵坐标值存放起来^[15].向量旋转中初始坐标为(x₀, y₀)=(K, 0)，其中K为校模因子且有：K=cos(φ₀)·cos(2^－3)·cos(2^－4)·cos(2^－5)···cos(2^－N－1)那么经过逆时针旋转φ₀后的坐标值为$\left\{ \begin{array}{l} {x_3} = {x_0}-\tan {\varphi _0} \cdot {y_0}\\ {y_3} = {y_0} + \tan {\varphi _0} \cdot {x_0} \end{array} \right. $，其中(x₃, y₃)即为改进算法第一阶段的初始迭代值.对于输出位宽N=16位(1位符号位和15位小数位)的改进CORDIC算法，输入角度位宽采用18位(4位角度范围和14位小数)，中间数据计算位宽采用18位以减少截断误差，当i≥(N-1)/2(即i≥7)时进行合并迭代.第一阶段将(x₃, y₃)作为初始迭代值，根据输入角度小数部分的高4位的位值以及对应的r_k进行式(3)所示的免查找表迭代，共迭代4次；第二阶段直接进行合并迭代，根据输入角度的高4位所指示的角度范围，对照表 1所示的角度映射和转换关系，对正余弦值做加减和缩放运算即可还原输出结果，算法整体结构见图 3.其中$\sqrt 2 /2 $近似为

$ \frac{{\sqrt 2 }}{2} \approx {2^{-1}} + {2^{-3}} + {2^{-4}} + {2^{ - 6}} + {2^{ - 8}} + {2^{ - 14}} + {2^{ - 16}}. $

(7)

因此$\sqrt 2 /2 $缩放可视为对数据进行移位连加操作.

4 仿真结果及分析

用Verilog HDL语言对传统流水线型CORDIC算法，三阶段CORDIC算法和免查找表CORDIC算法进行具体实现，在相同输出位宽的前提下，选用Xilinx公司的xc7k325t-2ffg900型号FPGA，利用ISE14.2自带的XST工具进行电路综合，得到寄存器和LUTs消耗情况以及最大输出时延见表 2.

寄存器的消耗主要取决于查找表的大小和迭代次数，最大输出时延与迭代次数有关.改进算法通过四次迭代替换查找表，又通过合并迭代减少大量的迭代，整体只需要5个时钟周期就能得到输出结果.比较三种算法使用的寄存器数量和最大输出时延可看出，改进算法使用的寄存器数量仅为流水线算法的25.58%，相比于三阶段算法节省了43.3%的寄存器消耗，最大输出时延相比于流水线型算法减少了68.75%.

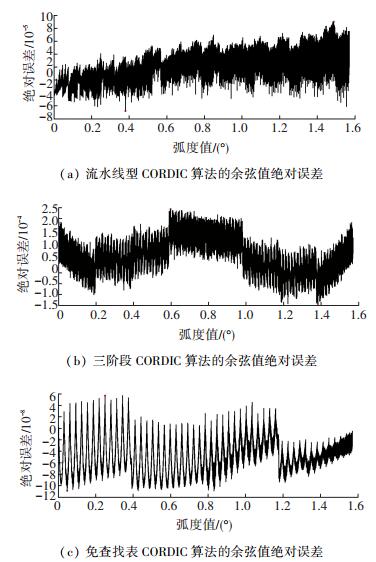
利用MATLAB对三种算法进行建模和误差分析，输入角度以2^-15分辨率遍历[0, π/2]，计算得到绝对误差. 表 3、4分别列出三种算法正余弦误差的最大值、最小值以及平均绝对误差值，其中三种算法的余弦值绝对误差如图 4所示，其中红色点代表的是绝对误差的最大值与最小值.通过比较三种算法的平均绝对误差值，可看出改进算法与流水线型算法的平均绝对误差处于同一数量级，但改进算法的平均绝对误差相对较小.和三阶段算法相比，改进算法的平均绝对误差相差一个数量级，其主要原因是在中间数据位宽较少时式(4)的近似误差较大，这一误差可通过采用更大的中间数据位宽来减小.

5 结论

针对传统流水线型CORDIC算法实现中存在的硬件资源消耗多、输出时延大等问题，结合角度二极化重编码、合并迭代以及角度区间折叠等技术提出了一种免查找表CORDIC算法.该算法将三阶段算法中的查找表替换为移位相加的迭代结构并省去了蝶形运算阶段，随后直接进行合并迭代，并根据角度映射关系还原输出结果.结果表明：与传统流水线型算法相比，免查找表算法的寄存器消耗减少了约74.42%，计算所需的时钟周期降低了68.75%.本文提出的免查找表CORDIC算法在实时性、输出精度、硬件资源消耗方面具有优势，适合高速实时的现代数字通信系统应用.