2. 北京新农村建设研究基地,北京 102206;
3. 北京航空航天大学 经管学院,北京 100191
2. Beijing Research Base for New Countryside Building, Beijing 102206, China;
3. School of Economics and Management, Beihang University, Beijing 100191, China
随着竞争的加剧,企业决策者面临的情形更复杂,比如当缺货发生,并不是所有的顾客都会缺失,会有一部分顾客允许延期交货.在现实中,当缺货发生时,许多因素会影响顾客允许延迟交货的意愿.比如顾客的喜好、耐心程度、折扣条件和商品可替代程度;换言之,允许延迟交货的概率会随着这些因素的变化而变化. Montgomery等[1]是第一批研究缺货和允许延期交货的学者文献[2-4]将该问题延伸到随机需求下连续盘点库存的优化问题中.
在库存模型中,如果服务水平约束(Service Level Constraint,SLC)取代缺货成本,这就意味着每期可用库存量和缺货量受到了限制文献[6],因此将服务水平约束引入库存模型取代缺货成文献[5]改进了文献[6]的工作,在目标函数中增加了缺货成本,并将再订货点作为决策变量.又有学者在Ouyang的目标函数基础上考虑服务约束水平,而不再考虑缺货成本.可见,在以往研究中,服务水平和缺货成本多是单独考虑的.因为服务水平约束比较容易建立,且方便计算,学者们渐渐用服务水平替代了缺货成本.但最近又有学者将服务水平和缺货成本同时考虑.因此,本文认为研究服务水平约束和缺货成本是否可以相互替代是很有必要的.
在关于库存策略的文章当中,需求分布基本都是确定的,文献[9]围绕零售系统在双源供应下向需求服从泊松分布的顾客提供服务的库存配置策略,文献[10]研究需求依赖于上一周期服务水平、缺货时订单部分损失的两周期易变质品库存问题.文献[11]研究需求服从均匀分布情形下存在顾客购买专业的双分销渠道的库存转运策略.已有研究针对需求服从自由分布的研究还比较少,因此本文主要讨论连续盘点的库存系统建立数学模型,并考虑了部分延迟交货情况下的最优订货量,同时建立了服务水平约束.当需求服从自由分布式时,采用Minmax方法来求最优订货量.数据分析部分的对比分析充分说明企业若想提高服务水平就必须付出更多的成本.
1 问题描述与假设本文考虑的是连续盘点库存决策问题,涉及符号及假设条件如下所示.
符号:A表示每次订货成本;D表示平均需求率;k表示安全系数;h表示每单位商品的持有成本;L表示提前期;Q表示订货量;β表示允许延迟交货的概率,β∈[0, 1];γ表示每单位商品的边际利润;π表示每单位商品的缺货成本;C(Q, L)表示总成本.
假设条件如下:(1)单位时间内,提前期需求服从均值为μL,方差为σL2=σ2L的正态分布. X1,X2,…,是独立同分布的自由变量. (2)库存是连续盘点的,每当库存水平降到R就补货.再订货点
提前期L由n个相互独立的部分组成.其中,提前期的第i(1≤i≤n)个组成部分有最短时间ai,正常时间bi,每压缩一个单位时间带来的赶工成本(额外增加的投入)为ci.为方便讨论,将提前期的n个相互独立的部分按照单位赶工成本中从小到大顺序重新排列,重新记作c1≤c2≤…≤ci≤…≤cn.提前期压缩时,优先考虑有最小的单位赶工成本的部分,依此类推.那么,
总成本为:
| $ \begin{align} & {\rm{min}}~EC\left( Q, L \right)= \\ & \frac{D\left( A+R\left( L \right)+\left( \pi +\gamma \left( 1-\beta \right) \right)E{{\left( X-R \right)}^{+}} \right)\rm{ }}{Q}\rm{ }+ \\ & h\left( \frac{Q}{2}+\left( 1-\beta \right)E{{\left( X-R \right)}^{+}}+k\sigma \sqrt{\mathit{L}}\rm{ } \right). \\ \end{align} $ | (1) |
对于确定的安全系数,它表示提前期需求超过再订货点的概率.实际上,没有被满足的需求比例不能超过某个确定值m.因此服务水平约束表述为
| $ \frac{E{{\left( X-R \right)}^{+}}}{Q}~\rm{ }\le \mathit{m, L}\in [{{\mathit{L}}_{\mathit{i}}}, {{\mathit{L}}_{\mathit{i}\rm{-}1}}]. $ | (2) |
提前期需求服从均值为μL和标准差为σL2=σ2L的自由分布. X1,X2,…,独立同分布的需求.此时,我们无法直接获得缺货期望E(X-R)+.因此,采用Minimax自由分布来解决问题.目标就是在约束水平下找到最小的总成本minEC(Q, L, k).在自由分布分析中,本文采用采用文献[7].
若X为随机变量,分布函数为F,均值为μL,方差为σ2L,那么
| $ E{\left( {X{\rm{ - }}r} \right)^ + } \le {\rm{ }}\frac{1}{2}{\rm{ }}[{\rm{ }}\sqrt {{\sigma ^2}\mathit{L} + {{\left( {\mathit{r}{\rm{-}}\mu L} \right)}^2}} {\rm{-}}\left( {r{\rm{-}}\mu L} \right)]. $ | (3) |
对于任何一个r,存在一个分布函数F*∈F,使上式成立.
由于
| $ E{\left( {X{\rm{ - }}R} \right)^ + } \le {\rm{ }}\frac{1}{2}\sigma \sqrt L {\rm{ }}\left( {\sqrt {1 + {k^2}} {\rm{ - }}k} \right){\rm{ }}. $ | (4) |
将不等式(4)代入(1),将k作为决策变量,则最大成本函数为
| $ \begin{array}{*{20}{l}} {{\rm{min}}EC\left( {Q,L,k} \right) = \frac{{D\left( {A + R\left( L \right)} \right)}}{Q} + }\\ {D\frac{{\left( {\pi + \gamma \left( {1{\rm{ - }}\beta } \right)} \right)\sigma \sqrt L M}}{{2Q}} + }\\ {h\left( {\frac{Q}{2} + \frac{{\left( {1{\rm{ - }}\beta } \right)\sigma \sqrt L M}}{2} + \sigma \sqrt L \frac{{1 - {M^2}}}{M}} \right),} \end{array} $ | (5) |
| $ \sigma \sqrt L M \le 2mQ. $ | (6) |
其中
不考虑约束进行求解,对Q、L求二阶导数
| $ \frac{{{\partial ^2}C}}{{\partial {Q^2}}} = \frac{{2D}}{{{Q^3}}}\left( {A + R\left( L \right) + \left( {\pi + \gamma \left( {1{\rm{ - }}\beta } \right)} \right)\sigma \sqrt L M} \right) > 0{\rm{ }}. $ | (7) |
因此,对于固定的M,L∈[Li, Li-1],EC(Q, L, M)是凸函数,
| $ \begin{array}{l} \frac{{{\partial ^2}EC\left( {Q, L, k} \right)}}{{\partial {L^2}}} = - \frac{D}{{8Q\frac{3}{2}\sqrt L }}(\pi + \gamma \left( {1{\rm{ - }}\beta } \right))\sigma M{\rm{ - }}\\ \frac{1}{{8\frac{3}{2}\sqrt L }}{\rm{ }}(h\left( {1{\rm{ - }}\beta } \right)\sigma M + 2\sigma \frac{{1{\rm{ - }}{M^2}}}{M}) < 0. \end{array} $ | (8) |
对于固定的M和Q,EC(Q, L, M)相对L是凹函数.
因此,对于确定的M和Q,当L的取值在区间[Li, Li-1]的端点时,总成本最小.
另外,对于固定的M和L∈[LiLi-1],
| $ {Q^*} = \sqrt {\frac{{2D}}{h}\left( {A + R\left( L \right) + \frac{1}{2}\left( {\pi + \gamma \left( {1{\rm{ - }}\beta } \right)} \right)\sigma \sqrt L M} \right)} $ | (9) |
当考虑约束时,如果
对M求一阶导和二阶导,并求解M和k,
| $ \begin{array}{l} \frac{{{\partial ^2}{\rm{E}}C\left( {Q, L, M} \right)}}{{\partial {M^2}}} = \frac{2}{{{M^3}}} > 0, \\ {M^*} = {\rm{ }}\sqrt {\frac{Q}{{h\beta Q - D\left( {\pi + \gamma \left( {1 - \beta } \right)} \right)}}} {\rm{ }}, \\ {k^*} = \frac{{1 - {M^2}}}{{2M}}{\rm{ }}. \end{array} $ | (10) |
如果
| $ \begin{array}{l} EC\left( M \right) = \frac{{2mD\left( {A + R\left( L \right)} \right)}}{{\sigma \sqrt L M}} + mD\left( {\pi + \gamma \left( {1 - \beta } \right)} \right) + \\ \frac{h}{2}\left( {\frac{{\sigma \sqrt L M}}{{2m}} + \left( {1 - \beta } \right)\sigma \sqrt L M + 2\sigma \sqrt L \frac{{1 - {M^2}}}{M}} \right){\rm{ }}. \end{array} $ | (11) |
解得
| $ \begin{array}{l} {M^{**}} = \sqrt {\frac{{4m\left( {2mD\left( {A + R\left( L \right)} \right) - h{\sigma ^2}L} \right)}}{{{\rm{ }}{\sigma ^2}Lh\left( {1 - 2m\left( {1 + \beta } \right)} \right)}}} {\rm{ }}\\ {k^*} = \frac{{1 - {M^2}}}{{2M}}. \end{array} $ |
计算步骤:
Step 1 将Li和ki带入式(9)计算Qi,i=1,2,……,n.
Step 2 将Li、Qi和ki代入式(1),计算总成本Ci.
Step 3 重复Step 1和Step 2,找到最小的Ci,即Ci′.
Step 4 将Ci′对应的Li′、Qi′和ki′代入服务水平约束.
若满足服务水平约束,则最优解(Li*,Qi*,ki*)=(Li′,Qi′,ki′).
若不满足服务水平约束,则将Li、Qi和ki代入服务水平约束,重复此步骤,找到所有符合约束的Li″、Qi″和ki″,其中,成本最小的就是最优解(Li′,Qi′,ki′).
3 算例分析本文采用以往文献数据[2]:D= 600 /年,σ= 7,π= $50,h = $20,A= $200,γ= $150,β= 0.5.提前期的三个组成部分如表 1所示.
| 表 1 提前期数据 Table 1 Lead time data |
根据上一节中求解步骤,得到需求服从自由分布时,不考虑缺货成本和服务水平约束,考虑缺货成本不考虑服务水平约束,不考虑缺货成本考虑服务水平约束,同时考虑缺货水平和服务水平约束情况下的最优库存策略,如图 1和图 2所示.
|
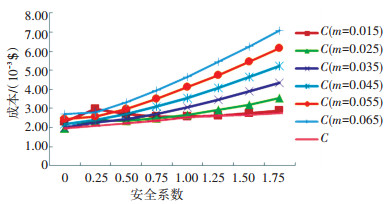
图 1 不考虑缺货时的库存策略 Figure 1 The inventory policy under different service level (without shortage) |

|
图 2 考虑缺货时的库存策略 Figure 2 The inventory policy under different service level (with shortage) |
从表 2可看出,需求服从自由分布情形下,采用minimax求解,所得最优订货量和最低成本均低于需求服从正态分布时的最优订货量和最低成本.无论需求服从正态分布还是自由分布,考虑服务水平约束情形下的最优订货量和最成本都远高于不考虑服务水平情形下的最优订货量和最低成本,因为考虑服务水平时,所付出的缺货成本要远高于其他成本.
| 表 2 不同需求分布和库存模型下的库存策略 Table 2 The inventory policy with different demand distribution and model |
图 1是不考虑缺货时不同服务水平下(m=0.015, m=0.025,m=0.035,m=0.045,m=0.055,m= 0.065)和不考虑服务约束时的库存策略曲线.通过图 1可知,考虑服务水平的期望总成本增加的速度大于不考虑缺货水平的增加速度,因此零售商若希望总成本最小,就必须放弃服务水平的要求.零售商若要求较高的服务水平,就必须付出更多的成本,二者不能兼得.
图 2是考虑缺货时不同服务水平下(m=0.015, m=0.025,m=0.035,m=0.045,m=0.055,m=0.065)和不考虑服务约束时的库存策略曲线. 图 2表明既考虑缺货成本又考虑服务水平约束情形下的库存策略.考虑服务水平情况下,当服务水平一定时,总成本随着安全库存的增加而增加;服务水平越高,增加速度越慢.不考虑服务水平的情形下,总成本随着安全库存增加而减少.
从图 1和图 2的对比我们可以看到,考虑缺货要比不考虑缺货付出更多的成本.因此,可以说,企业为了提高服务水平就要尽量避免缺货出现,就必须付出更多成本来维持服务水平.也就是说将服务水平和缺货成本同时考虑,可以让企业清楚的知道每提高1%的服务水平所付出的成本,如果零售商只单独考虑服务水平或者缺货成本,零售商就无法知道自己损失的掉的成本或者服务水平是多少,也就无法整体把握企业的运营情况,也就很难改进绩效增加利润.因此,必须将成本和服务水平同时考虑,找到二者的最佳结合点,才能使企业在竞争中灵活地调整策略,来争取竞争优势.
4 结论本章考虑连续盘点库存的优化问题,建立包括订货成本、提前期压缩成本、库存成本和缺货成本的总成本函数,同时构建了服务水平约束条件.针对需求服从自由分布情形下对最优订货量进行求解.通过算例分析可知,考虑缺货成本情形下的期望总成本随着安全系数的增加而减少,不考虑缺货成本情形下的期望总成本随着安全系数的增加而增加.考虑服务水平的期望总成本增加的速度大于不考虑缺货水平的增加速度,因此零售商若希望总成本最小,就必须放弃服务水平的要求.考虑缺货成本又考虑服务水平约束情形下的库存策略.考虑服务水平情况下,当服务水平一定时,总成本随着安全库存的增加而增加;服务水平越高,增加速度越慢.不考虑服务水平的情形下,总成本随着安全库存增加而减少.
| [1] |
MONTGOMERY D C, BAZARAA M S, KESWANI A.K. Inventory models with a mixture of backorders and lost sales[J].
Naval Research Logistics Quarterly, 1973, 20: 255-264.
DOI: 10.1002/(ISSN)1931-9193 |
| [2] |
OUYANG L Y, CHUANG B R, LIN Y J. Effective investment to reduce lost-sales rate in a periodic review inventory model[J].
OR Spectrum, 2007, 29: 681-697.
DOI: 10.1007/s00291-007-0081-8 |
| [3] |
JHA J K, SHANKER K. Two-echelon supply chain inventory model with controllable lead time and service level constraint[J].
Computers & Industrial Engineering, 2009, 57: 1096-1104.
|
| [4] |
YE Fei, XU Xuejun. Cost allocation model for optimizing supply chain inventory with controllable lead time[J].
Computers & Industrial Engineering, 2010, 59: 93-99.
|
| [5] |
OUYANG L Y, WU K. S, HO C H. Integrated vendor-buyer cooperative models with stochastic demand in controllable lead time[J].
International Journal of Production Economics, 2004, 92: 255-266.
DOI: 10.1016/j.ijpe.2003.10.016 |
| [6] |
PAN J C H, HSIAO Y C, LEE C J. Inventory models with fixed and variable lead time crash costs considerations[J].
Journal of the Operational Research Society, 2002, 53: 1048-1053.
DOI: 10.1057/palgrave.jors.2601354 |
| [7] |
GALLEGO G, MOON I. The distribution free newsboy problem: Review and extensions[J].
The Journal of the Operational Research Society, 1993, 44: 825-834.
DOI: 10.1057/jors.1993.141 |
| [8] |
WANG Xiaobin. Continuous review inventory model with variable lead time in a fuzzy random environment[J].
Expert Systems with Applications, 2011, 38: 11715-11721.
DOI: 10.1016/j.eswa.2011.03.057 |
| [9] |
刘名武, 魏晓梅. 两类需求下双源供应的库存配置策略[J].
系统工程, 2016, 34(4): 84-88.
|
| [10] |
段永瑞, 傅琼超, 李贵萍. 需求依赖于服务水平的易变质品库存策略研究[J].
运筹与管理, 2015, 24(6): 65-75.
|
| [11] |
赵秋红, 朱少楠, 李安楠. 存在顾客购买转移的双分销渠道订货与库存转运策略[J].
系统工程理论与实践, 2014, 34(6): 1453-1461.
DOI: 10.12011/1000-6788(2014)6-1453 |
| [12] |
SARKAR B, CHAUDHURI K, MOON I. Manufacturing setup cost reduction and quality improvement for the distribution free continuous-review inventory model with a service level constraint[J].
Journal of Manufacturing Systems, 2015, 34: 74-82.
DOI: 10.1016/j.jmsy.2014.11.003 |
| [13] |
KAMBUROWSKIJ. On the distribution-free newsboy problem with some non-skewed demands[J].
Operations Research Letters, 2015, 43(2): 165-171.
DOI: 10.1016/j.orl.2015.01.005 |
| [14] |
KWON K, CHEONG T. A minimax distribution-free procedure for a newsvendor problem with free shipping[J].
European Journal of Operational Research, 2014, 232(1): 234-240.
DOI: 10.1016/j.ejor.2013.07.004 |
| [15] |
BIDKHORI H, SIMCHI-LEVI D, WEI Yehua. Analyzing process flexibility: A distribution-free approach with partial expectations[J].
Operations Research Letters, 2016, 44(3): 291-296.
DOI: 10.1016/j.orl.2016.02.008 |
 2017, Vol. 49
2017, Vol. 49


