灌浆料作为重要的连接锚固材料,在预制装配结构钢筋灌浆套筒接头中使用最多,建筑结构改造加固中,灌浆料由于流动性好、快硬、早强,工程运用也越来越多.
国内外文献对灌浆料与钢筋的黏结滑移关系研究甚少.仅2016年,王建超等[1]对18个灌浆套筒接头进行单轴拉伸试验,研究灌浆料强度和钢筋直径对钢筋与灌浆料的黏结-滑移关系及破坏特征的影响.
目前,对钢筋与混凝土黏结性能的研究较为成熟.1957年, Plowman[2]进行了黏结试验,证明了带肋钢筋黏结强度与混凝土抗拉强度有关.1998年,Zuo等[3]发现混凝土骨料也会在不同程度上影响黏结强度.2000年,Yerlici等[4]通过混凝土与带肋钢筋的拔出试验,发现黏结强度随混凝土保护层厚度的增大而增大,但超过临界保护层厚度之后对黏结性能就没有明显影响了;黏结强度随钢筋直径增大而减小,且与钢筋直径的平方根成反比关系.2005年,Kheder[5]通过研究钢筋与普通及高强混凝土之间的黏结性能,再次验证了黏结强度与相对保护层厚度呈正相关,与钢筋直径呈负相关,并给出了黏结强度与混凝土抗压强度关系.
套筒灌浆接头有限元分析中,钢筋与灌浆料的黏结-滑移本构关系基本采用混凝土与钢筋的关系式[6],但灌浆料无粗骨料,峰值应变大于混凝土,弹性模量小于混凝土,抗裂性好于混凝土,其与钢筋间黏结滑移关系是否等同混凝土与钢筋间的关系,各影响因素变化对黏结性能的改变是否和混凝土研究结果一致,这些问题有待研究.
本文进行了9组27个带肋钢筋-灌浆料拉拔试验,分析保护层厚度、钢筋直径和钢筋锚固长度对试件黏结性能的影响.并与现有文献的钢筋与混凝土锚固试验结果对比,衡量钢筋与灌浆料、混凝土黏结性能差异.为钢筋在灌浆料中锚固长度计算及灌浆套筒接头的有限元分析提供理论基础.
1 试验概况 1.1 材性试验本试验使用HRB400级钢筋,通过拉伸试验得到基本力学指标见表 1.
| 表 1 钢筋力学参数 Table 1 Mechanical parameters of reinforced bar |
试验所用灌浆料为上海环宇建筑工程材料有限公司生产的H-40灌浆料.根据GB/T 17671—1999《水泥胶砂强度检验方法》[7]和GB/T 50081—2002《普通混凝土力学性能试验方法标准》[8],测得40 mm×40 mm×160 mm灌浆料棱柱体标准试块抗压强度为58.83 MPa;测得150 mm×150 mm×150 mm灌浆料立方体试块劈裂抗拉强度为3.89 MPa.
1.2 试件和参数设计试验共有27个试件,考虑保护层厚度、钢筋直径和钢筋锚固长度3个参数的影响,试件的编号及参数见表 2.
| 表 2 试件参数汇总表 Table 2 Parameters of specimens |
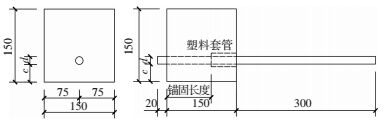
试件的外形和尺寸如图 1所示.试件制作时,预埋不同长度的PVC硬质套管,用于调整钢筋的锚固长度.PVC套管和钢筋之间需填充泡沫塑料以防止漏浆.按照每25 kg灌浆料配3.3 kg清水的比例配置灌浆料浆体,搅拌均匀后浇筑到木模内,养护28 d.
|
图 1 钢筋拉拔试验基准试件尺寸(mm) Figure 1 The benchmark specimen size for steel drawing test(mm) |
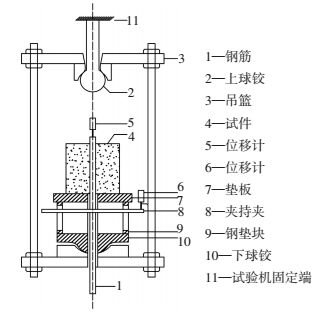
试验所用加载装置为最大可提供500 kN拉力的SANS-CMT5505万能电子试验机.加载装置见图 2.试验采用单调加载,力控制方式,加载速度为100 N/s,系统每秒采集记录30组数据.
|
图 2 加载装置示意 Figure 2 Schematic diagram of loading device |
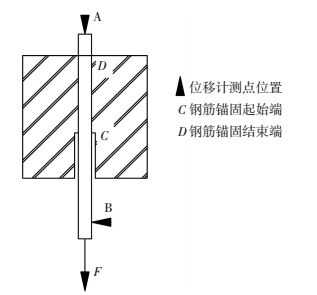
图 3为位移计测点位置示意图.忽略灌浆料变形,位移计A测得数据即为D点自由端位移sF;位移计B扣除未锚入灌浆料的BC段钢筋变形ΔsL=εBC×lBC,即为C点加载端位移sL.除特别说明外,文中黏结锚固滑移采用均值
|
图 3 位移计测点位置 Figure 3 Measuring point position of displacement meter |
钢筋与混凝土的平均黏结锚固应力τ为
| $ \bar \tau = \frac{F}{{{\rm{ \mathsf{ π} }}d{l_{\rm{a}}}}}, $ | (1) |
式中:F为拉拔力,la为锚固长度,d为钢筋直径.
当拉拔力F达到峰值Fu时得到的平均黏结锚固应力称为黏结锚固强度τu.试件达到黏结锚固强度时对应的滑移值为su=s.
2 试件破坏类型本试验9组试件的破坏类型如表 3所示(每组3个试件破坏形态一致).试件破坏形态有3种:
| 表 3 试件破坏类型 Table 3 Failure type of specimens |
1) 灌浆料劈裂破坏:由于没有配置箍筋,大多数试件发生劈裂破坏.发生钢筋屈服前劈裂破坏的试件见图 4(a),发生钢筋屈服后劈裂破坏的试件见图 4(b).

|
图 4 试件破坏形态 Figure 4 Failure patterns of specimens |
2) 钢筋拔出破坏:当相对保护层厚度过大或钢筋锚固长度过小时,试件发生钢筋拔出破坏,钢筋肋间充满灌浆料碎屑,见图 4(c).锚固长度较短的试件钢筋未屈服就拔出,锚固长度较长的试件在钢筋屈服后拔出.
3) 钢筋拉断破坏:由于钢筋锚固长度较长,黏结力足够大,当试件所受荷载持续增加,钢筋逐渐屈服并发生“颈缩”现象,钢筋拉断破坏.见图 4(d).
带肋钢筋与灌浆料的黏结作用由三部分组成:1)灌浆料水泥胶体与钢筋表面的化学胶着力;2)钢筋与灌浆料接触面上的摩擦力;3)肋与灌浆料的机械咬合作用.
化学胶着力很小,加载初期很快被克服,黏结力主要由摩擦力和机械咬合力提供.
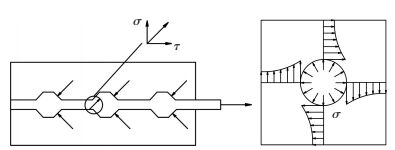
钢筋受力时,钢筋与灌浆料的作用力见图 5,可分解为轴向和径向应力分量.轴向应力使灌浆料受剪,径向应力则引起灌浆料中的环向拉力.
|
图 5 灌浆料黏结机理示意 Figure 5 Sketch map of grouting material bonding mechanism |
3种破坏形态的力学机理如下:当灌浆料的环向拉力足够大,而试件的保护层厚度较小,灌浆料发生劈裂破坏;当剪力足够大,克服钢筋与灌浆料接触面上摩擦力及机械咬合力时,试件发生钢筋拔出破坏;当环向拉力尚未使灌浆料劈裂、剪力尚未使咬合齿失效,钢筋就先屈服,试件发生钢筋拉断破坏.
3 黏结强度影响因素 3.1 保护层厚度本试验通过偏心置筋的方式改变保护层厚度.表 4为不同保护层厚度下试件的黏结强度,可以看出,随着保护层厚度的增大,试件的极限荷载(黏结强度)不断增大.保护层厚度达到5d时,试件已经从劈裂破坏转变为钢筋拔出破坏,灌浆料保护层所提供的抗劈裂能力已经足够大,可以预见继续增大保护层厚度将不会对极限黏结强度产生明显影响.
| 表 4 不同保护层厚度下试件的黏结强度 Table 4 The bond strength of the specimens under different cover thickness |
为便于与其他学者研究成果进行对比,用一次函数对黏结强度与相对保护层厚度关系进行拟合,拟合公式为
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{{\rm{ts}}}}}} = 5.94 + 0.13\left( {\frac{c}{d}} \right), $ | (2) |
式中fts为劈裂抗拉强度,当c/d>5时取c/d=5.
图 6为黏结强度与相对保护层厚度拟合曲线与试验数据点的对比.
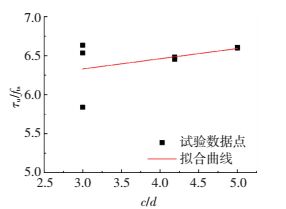
|
图 6 不同保护层厚度下黏结强度试验值拟合曲线 Figure 6 Fitting curve of bond strength test values under different cover thickness |
徐有邻等[9]通过对带肋钢筋与普通混凝土的黏结锚固性能的试验研究,得到
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{\rm{t}}}}} = 1.6 + 0.7\left( {\frac{c}{d}} \right), $ | (3) |
式中ft为轴心抗拉强度,当c/d>4.5时取c/d=4.5.
王国杰[10]对钢筋与高强度自密实混凝土黏结锚固性能的试验研究,得到
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{\rm{t}}}}} = 5.214 + 0.585\left( {\frac{c}{d}} \right). $ | (4) |
现将式(3)、(4)中的轴心抗拉强度换算为劈裂抗拉强度.尹健等[11]通过试验给出了较精确的混凝土劈裂抗拉强度与轴心抗拉强度的换算公式,即ft=0.921fts.式(3)、(4)分别改写为:
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{{\rm{ts}}}}}} = 1.47 + 0.64\left( {\frac{c}{d}} \right), $ | (5) |
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{{\rm{ts}}}}}} = 4.8 + 0.54\left( {\frac{c}{d}} \right). $ | (6) |
图 7为式(2)、(5)、(6)三种黏结强度与相对保护层厚度关系式的对比,可以看出,灌浆料的斜率低于普通混凝土和自密实混凝土.由于混凝土有粗骨料,可提高抗劈裂能力,故保护层厚度增大相同幅度,混凝土黏结强度增长快,灌浆料黏结强度增长慢.
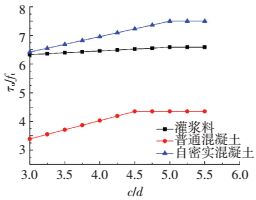
|
图 7 灌浆料与不同混凝土黏结强度公式对比 Figure 7 Comparison of bond strength formulas between grout and different kind of concretes |
表 5为保护层厚度均为67 mm的不同钢筋直径试件的黏结强度,可以看出,随着钢筋直径的增大,钢筋与灌浆料的黏结强度却不断降低.这是因为本试验的这3组试件虽然保护层厚度基本一致,但其相对保护层厚度却差异较大,随着钢筋直径增大,钢筋的相对保护层厚度c/d却由4.19下降到了3.35.对于发生劈裂破坏的试件,在其他情况相同时,绝对保护层厚度在一定程度上决定了试件所能承受的极限荷载,而相对保护层厚度决定了试件的黏结强度.因此,随着钢筋直径的增加,试件的极限荷载变化不大,平均黏结强度却越来越小.
| 表 5 不同钢筋直径试件的黏结强度 Table 5 The bond strength of specimens with different bar diameter |
利用一次函数式对黏结强度τu, m/fts-c/d进行拟合,得到式(7),不同钢筋直径下黏结强度试验值的拟合曲线见图 8.
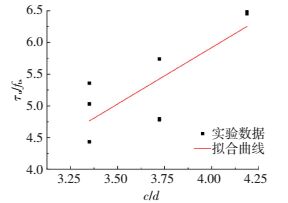
|
图 8 不同钢筋直径下黏结强度试验值拟合曲线 Figure 8 The bond strength fitting curve under different bar diameters |
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{{\rm{ts}}}}}} = - 1.2 + 1.78\left( {\frac{c}{d}} \right). $ | (7) |
不同钢筋锚固长度试件的黏结强度如表 6所示,随着钢筋锚固长度的增加,试件所能承受的极限荷载不断增加.这是由于增加钢筋锚固长度加大了钢筋与灌浆料之间的接触面积和机械咬合作用,因此试件所能承受的极限荷载有了明显提升.
| 表 6 不同钢筋锚固长度试件的黏结强度 Table 6 The bond strength of the specimens under different anchorage length of steel bar |
当钢筋锚固长度达到8d时,试件为拉断破坏,可以预见,再继续增加钢筋锚固长度,试件的承载能力也不会有明显变化.
随着钢筋锚固长度的增加,试件的平均黏结强度降低.这是由于黏结应力沿钢筋纵向分布是不均匀的,一般来说靠近加载端的黏结应力较大,靠近自由端的黏结应力较小.当钢筋锚固长度较小时,黏结应力分布相对均匀,平均黏结强度τu与实际最大黏结应力τmax的比值较大,而当锚固长度较大时,黏结应力分布不均匀,平均黏结强度τu与实际最大黏结应力τmax的比值较小.不同钢筋锚固长度的试件τmax的变化不大,因此随着钢筋锚固长度的增加,试件的平均黏结应力越来越小.
图 9为不同锚固长度下黏结强度试验值的拟合曲线.C1组由于钢筋锚固长度过短造成的拔出破坏工程中是应当避免出现的,因此试件数据不参与公式拟合.拟合式为
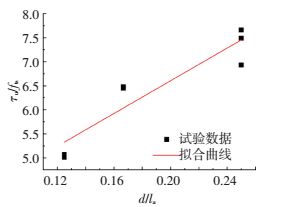
|
图 9 不同锚固长度下黏结强度试验值拟合曲线 Figure 9 The bond strength fitting curve under different anchorage length of steel bars |
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{{\rm{ts}}}}}} = 3.20 + 17.0\left( {\frac{d}{{{l_{\rm{a}}}}}} \right), $ | (8) |
式中d/la≤1/4.
山显彬[12]通过带肋钢筋与自密实混凝土的黏结锚固试验,得到
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{{\rm{ts}}}}}} = 3.22 + 10.01\left( {\frac{d}{{{l_{\rm{a}}}}}} \right). $ | (9) |
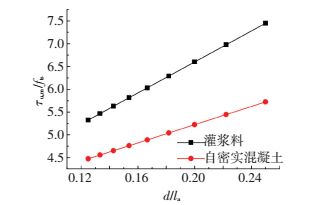
图 10为式(8)、(9)两种黏结强度与钢筋锚固长度关系式的对比,灌浆料曲线斜率较大,即相比于自密实混凝土,锚固长度增加相同幅度,灌浆料黏结强度增长快.
|
图 10 灌浆料与混凝土的钢筋锚固长度对比 Figure 10 Comparison of steel bar anchoring length in grout and concrete |
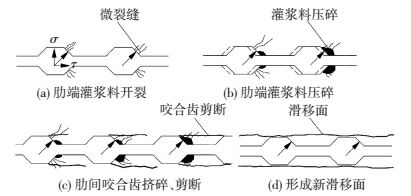
当加载端荷载较小时,肋间灌浆料近似线弹性变形,此时钢筋与灌浆料间的相对滑移很小,灌浆料中的微裂缝开始慢慢发展,如图 11(a)所示;随着荷载继续增加,到达钢筋屈服点附近时,钢筋自身的变形迅速加大,切向分量τ引起的肋间灌浆料剪力使得肋端灌浆料大面积压碎,钢筋与灌浆料间的相对滑移开始增大,肋间灌浆料进入非线性变形阶段,如图 11(b)所示;接近极限荷载时,肋前灌浆料破碎加剧,范围扩大,最终挤压破碎剥落,达最大承载力,之后荷载开始迅速下降,滑移继续较快增长,咬合齿剪断,钢筋开始慢慢被拔出,如图 11(c)所示;随后,钢筋与灌浆料间形成新的滑移面,该滑移面与灌浆料试块之间仍保持有一定的摩擦力,并延续到钢筋被完全拔出,如图 11(d)所示.
|
图 11 灌浆料开裂、压碎和剪断过程 Figure 11 The grouting material cracking, crushing and shearing process |
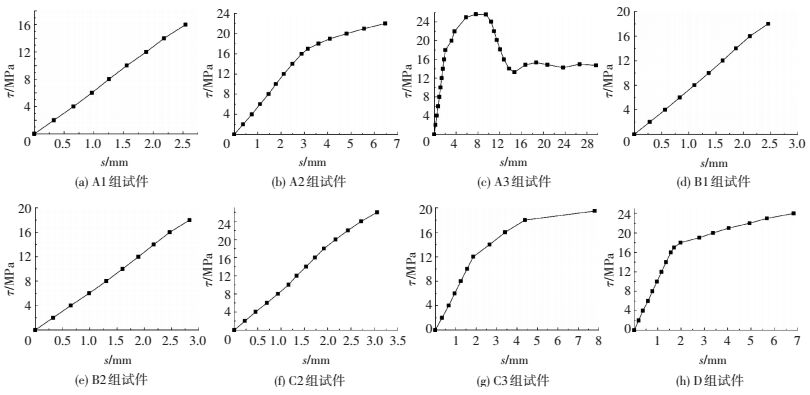
各组试件的平均τ-s曲线见图 12.由图 12可以看出,虽然各组试件破坏时平均τ-s曲线所处的阶段不同,但曲线形式具有相似的特征(C1组试件除外,后文叙述).典型的灌浆料与带肋钢筋之间黏结应力-滑移曲线见图 13,曲线划分为4个阶段:
|
图 12 各组试件的平均τ-s曲线 Figure 12 Average τ-s curve |

|
图 13 典型平均τ-s曲线 Figure 13 Average τ-s curve |
1) 线性段(0-s):试件加载初期黏结应力增长较快,但滑移值增长相对缓慢,τ-s曲线基本呈线性关系,斜率较大.此阶段,钢筋周围灌浆料开始出现微裂缝,并逐渐向试件表面扩展,过程对应图 11(a).在线性段末期,肋前灌浆料开始出现被压碎的迹象.
2) 滑移加速段(s-u):进入滑移加速段,前期曲线仍近似为线性,后期出现非线性特征,τ-s曲线斜率明显变小.此时黏结应力增长速度放缓,而滑移量增长速度加快,钢筋肋前灌浆料被大面积压碎,过程对应图 11(b).A1、A2、B1、B2、C2、C3、D组试件在该阶段发生破坏,C3为钢筋拉断破坏,其余均为劈裂破坏.
3) 下降段(u-r):达到极限黏结强度后,发生钢筋拔出破坏的试件τ-s曲线进入下降段.此阶段,钢筋肋间灌浆料在压碎和剪断的共同作用下失效,机械咬合力逐渐丧失,黏结应力持续下降.过程对应图 11(c).
4) 残余段(r-):当黏结应力下降到约为0.5τu之后,保持在一定水平上下略有波动,而滑移值则不断增大,直到钢筋被完全拔出.钢筋横肋与横肋间的灌浆料碎屑共同组成新的滑移面.该过程对应图 11(d).A3组试件在该阶段发生破坏.
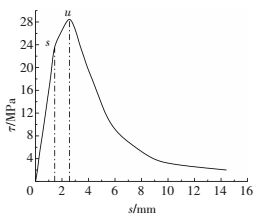
C1组试件为短锚拔出破坏,τ-s曲线如图 14所示,上升段特征与典型曲线相同,当黏结应力达到约0.85τu时,曲线进入滑移加速段.当达到极限黏结应力,曲线迅速下降,滑移持续增加,但由于锚固长度过短,新的滑移面无法提供强大的摩擦力,所以残余段的黏结强度接近零.
|
图 14 C1试件的平均τ-s曲线 Figure 14 Average τ-s curve of C1 |
为了便于工程应用及有限元分析,本文参照Mirza等[13]提出的四阶多项式黏结应力-滑移关系,以式(10)为模型,忽略与其他组τ-s曲线形状有较大不同的C1组试件的试验结果,将其余组试件的试验数据统计回归得出式(11).
| $ \tau = {k_1}{s^4} + {k_2}{s^3} + {k_3}{s^2} + {k_4}s, $ | (10) |
| $ \tau = - 4.05 \times {10^{ - 3}}{s^4} + 0.124{s^3} - 1.56{s^2} + 9.55s. $ | (11) |
式中:τ为平均黏结应力,MPa;s为平均滑移,mm.0≤s≤su,当s≥14时,取s=14.
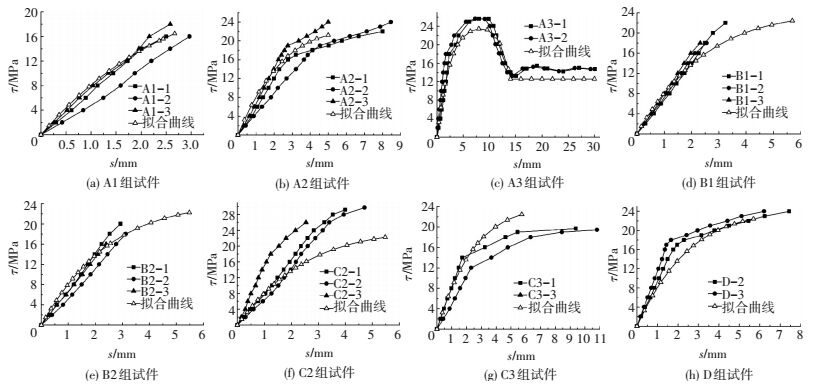
式(11)拟合曲线与试验数据对比见图 15.曲线拟合情况良好.
|
图 15 各组试件τ-s曲线与拟合曲线对比 Figure 15 Comparison of each specimen's τ-s curves to fitting curve |
根据前面的分析,黏结锚固强度与保护层厚度、钢筋直径、锚固长度有关.此外,钢筋的肋对灌浆料的挤压力引起肋前斜裂以及纵向劈裂,因此黏结强度也与灌浆料的抗拉强度有关.
国内学者对钢筋与不同类型混凝土的黏结强度公式进行研究:
1990年,徐有邻[14]通过大量试验,基于试验数据的统计回归,提出了黏结强度表达式:
| $ {\tau _{\rm{u}}} = \left[ {0.82 + 0.9\left( {\frac{d}{{{l_{\rm{a}}}}}} \right)} \right]\left[ {1.6 + 0.7\left( {\frac{c}{d}} \right) + 20{\rho _{{\rm{sv}}}}} \right]{f_{\rm{t}}}, $ | (12) |
式中ρsv为配箍率,ft为混凝土轴心抗拉强度.
王冰等[15]提出了钢筋与浮石混凝土黏结强度公式:
| $ {\tau _{\rm{u}}} = \left[ {0.56 + 2.18\left( {\frac{d}{{{l_{\rm{a}}}}}} \right)} \right]\left[ {3.74 + 0.62\left( {\frac{c}{d}} \right) + 10\sqrt {{\rho _{{\rm{sv}}}}} } \right]{f_{\rm{t}}}. $ | (13) |
李渝军等[16]提出了钢筋与高强陶粒混凝土黏结强度公式:
| $ {\tau _{\rm{u}}} = \left[ {0.30 + 3.5\left( {\frac{d}{{{l_{\rm{a}}}}}} \right)} \right]\left[ {0.36 + 0.45\left( {\frac{c}{d}} \right) + 4.1\sqrt {{\rho _{{\rm{sv}}}}} } \right]f_{{\rm{cu}}}^{0.55}. $ | (14) |
式中fcu为高强陶粒混凝土立方体抗压强度.
山显彬[12]通过钢筋拉拔试验拟合出了带肋钢筋与自密实混凝土的黏结强度公式:
| $ {\tau _{\rm{u}}} = \left[ {0.63 + 1.96\left( {\frac{d}{{{l_{\rm{a}}}}}} \right)} \right]\left[ {2.14 + 0.67\left( {\frac{c}{d}} \right) + 34.79{\rho _{{\rm{sv}}}}} \right]{f_{{\rm{ts}}}}, $ | (15) |
式中fts为自密实混凝土劈裂抗拉强度.
贾方方[17]提出了带肋钢筋与掺有钢纤维的活性粉末混凝土的黏结强度公式:
| $ \begin{array}{l} {\tau _{\rm{u}}} = \left[ {2.675 + 0.711\left( {\frac{c}{d}} \right)} \right]\left[ {0.65 + 1.257\left( {\frac{d}{{{l_{\rm{a}}}}}} \right)} \right] \cdot \\ \;\;\;\;\;\;\;\left( {0.815 + 0.1{V_{\rm{f}}}} \right)\sqrt {{f_{{\rm{cu}}}}} , \end{array} $ | (16) |
式中Vf为钢纤维体积掺量.
本文参考上述混凝土与钢筋黏结强度公式,基于本次试验数据的统计回归,提出带肋钢筋与灌浆料的平均黏结强度公式:
| $ {\tau _{\rm{u}}} = \left[ {0.94 + 0.50\left( {\frac{d}{{{l_{\rm{a}}}}}} \right)} \right]\left[ {3.02 + 0.71\left( {\frac{c}{d}} \right)} \right]{f_{{\rm{ts}}}}. $ | (17) |
本次试验平均黏结强度试验值τu, c与计算值τu, 0对比见表 7.τu, 0/τu, c的平均值为1.02,标准差为0.13,变异系数为0.13,公式拟合良好.
| 表 7 灌浆料模型平均黏结强度试验值与计算值对比 Table 7 Comparison of test value and calculated value of grout bond strength model |
将试验参数c、d、la、fts代入上述不同模型计算公式中,得到不同模型平均黏结强度计算值τu, 0,见表 8.
| 表 8 不同材料模型黏结强度对比 Table 8 Comparison of bond strength in different material model |
可以看出,相同试验条件下,只有活性粉末混凝土的平均黏结强度高于灌浆料,浮石混凝土的平均黏结强度与灌浆料最为接近,混凝土、自密实混凝土的平均黏结强度较低.
由于灌浆料或混凝土对黏结强度的影响主要是通过其抗劈裂能力来体现的,在各类混凝土和灌浆料强度等级近似相同时,骨料强度越低则砂浆强度相对就越大,其与钢筋的黏结强度就越高.在表 8的6组模型中,活性粉末混凝土没有粗骨料,同时掺入了硅粉和高效减水剂等外加剂,所以其黏结强度最大.灌浆料试件中没有掺加骨料,但也没有加入活性材料和外加剂,因此黏结强度较高但不如活性粉末混凝土.浮石混凝土中的粗骨料浮石强度很低,甚至远低于水泥石,所以其砂浆强度相对较高,与钢筋的黏结强度也较高.混凝土、自密实混凝土中有粗骨料,砂浆强度低,所以其黏结强度也较灌浆料低.
5.2 黏结强度对应滑移值su试件达到极限荷载时,平均黏结强度对应的滑移值为su(以下简称黏结滑移值).经试验数据统计回归,得到黏结滑移值公式:
| $ {s_{\rm{u}}} = - 0.099{\left( {{\tau _{\rm{u}}} - 23.23} \right)^2} + 5.73. $ | (18) |
灌浆料黏结滑移值su的试验值与公式计算值对比见表 9.su, 0/su, c平均值为1.22,标准差为0.57,变异系数为0.47,公式拟合良好.
| 表 9 灌浆料黏结滑移试验值与计算值对比 Table 9 Comparison of test value and calculated value of grout bond-slip model |
将本试验参数d代入文献[14-16, 18]黏结滑移值公式中,得到表 10的不同材料模型黏结滑移值对比.相关文献的黏结滑移公式是在试件拔出破坏下得出的,故选取灌浆料中带肋钢筋拔出破坏的工况与不同材料模型的黏结滑移值进行对比.
| 表 10 不同材料黏结强度对应滑移值对比 Table 10 Comparison of different material model bond-slip |
对比发现,钢筋与灌浆料达到黏结锚固强度时所对应的滑移值远大于混凝土.这是由于灌浆料不含骨料,导致灌浆料弹性模量较小,所以在相同应力下,肋间灌浆料变形比混凝土要大,这在一定程度上造成钢筋与灌浆料之间的滑移量大于混凝土.
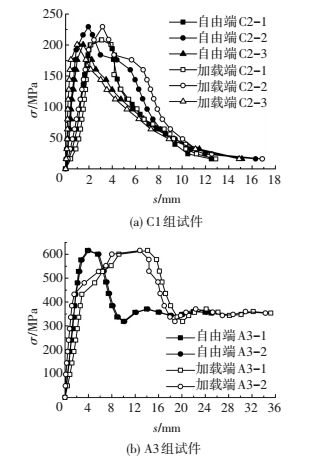
表 10中,A3组试件滑移值明显大于C1组.图 16为C1、A3组试件自由端和加载端位移与钢筋应力关系曲线.A3组自由端、加载端位移均大于C1组.
|
图 16 自由端和加载端位移与钢筋应力关系曲线 Figure 16 The free end and loading end displacement curve relationship with reinforcement stress |
C1组为钢筋屈服前拔出破坏,自由端和加载端位移始终差别不大,由于钢筋未屈服,自由端和加载端σ-s曲线的上升段,均近似为一条直线,没有明显转折.A3为钢筋屈服后拔出破坏,自由端σ-s曲线的上升段近似为一条直线,而加载端σ-s曲线的上升段在达到钢筋屈服强度时却发生了明显转折.
A3组试件锚入灌浆料部分近加载端的钢筋可能屈服甚至发生强化,钢筋屈服或强化将会对钢筋与灌浆料之间的应力分布产生重大影响,钢筋弹性模量明显变小,伸长量迅速增加,但是肋间灌浆料形成的咬合齿又阻止钢筋的伸长,所以力大幅度转移到肋间灌浆料咬合齿上,导致肋间灌浆料变形增大,故A3组滑移值明显大于C1组,曲线出现类似屈服平台和强化段.
6 钢筋锚固长度设计建议 6.1 试验及统计资料 6.1.1 钢筋参数按照95%的保证率来求得带肋钢筋屈服强度的平均值:
| $ {\mu _{{f_{\rm{y}}}}} = \frac{{{f_{{{\rm{y}}_{\rm{k}}}}}}}{{1 - 1.645{\delta _{{f_{\rm{y}}}}}}} = 456, $ | (19) |
式中fyk为钢筋强度标准值,δfy为钢筋强度变异系数,按照钢筋拉伸试验数据计算得到钢筋强度变异系数为
| $ {\delta _{{f_{\rm{y}}}}} = 0.0744. $ | (20) |
根据试验中灌浆料劈裂抗拉实测数据统计,得到劈裂抗拉强度fts的平均值和变异系数分别为:
| $ {\mu _{{f_{{\rm{ts}}}}}} = 3.89, $ | (21) |
| $ {\delta _{{f_{{\rm{ts}}}}}} = 0.048. $ | (22) |
灌浆料试件几何尺寸的偏差包括钢筋锚固长度、保护层厚度和钢筋直径,参考普通混凝土[14]试件几何尺寸的偏差,见表 11.
| 表 11 构件几何尺寸偏差统计 Table 11 Geometric dimension deviation statistics |
当试件的锚固力等于钢筋屈服力时,锚固长度为临界锚固长度,用lacr来表示.
锚固力为Fu=τu·πdlacr,钢筋屈服力为Fy=fyπd2/4.根据平衡条件,得锚固承载力极限状态方程为
| $ 4\left( {\frac{{l_{\rm{a}}^{{\rm{cr}}}}}{d}} \right){\tau _{\rm{u}}} = {f_{\rm{y}}}. $ | (23) |
令R=4(lacr/d)τu,S=fy.
将式(23)改写为更通用的形式R=S.
式中:R为锚固抗力,与锚固长度和黏结锚固强度有关;S为结构或构件中因作用引起的效应,即对锚固钢筋的拉拔力.
为反映式(17)黏结强度公式τu的准确性,引入系数Ω=τu, 0/τu, c,由表 6知,系数Ω的平均值μΩ=1.02,变异系数δΩ=0.13.
故抗力R修正为
| $ R = \mathit{\Omega } \cdot 4\left( {l_{\rm{a}}^{{\rm{cr}}}/d} \right){\tau _{\rm{u}}}. $ | (24) |
将式(17)τu表达式代入式(24),得
| $ R = 4\Omega \cdot \left[ {0.50 + 0.94\left( {\frac{{l_{\rm{a}}^{{\rm{cr}}}}}{d}} \right)} \right]\left[ {3.02 + 0.71\left( {\frac{c}{d}} \right)} \right]{f_{{\rm{ts}}}}. $ | (25) |
令
| $ {L_1} = 0.50 + 0.94\left( {\frac{{l_{\rm{a}}^{{\rm{cr}}}}}{d}} \right), $ |
| $ {T_1} = 3.02 + 0.71\left( {\frac{c}{d}} \right). $ |
则式(25)简化为
| $ R = 4\mathit{\Omega } \cdot {L_1} \cdot {T_1} \cdot {f_{{\rm{ts}}}}. $ | (26) |
考虑构件la、d尺寸偏差,L1的平均值、标准差和变异系数为:
| $ {\mu _{{{\rm{L}}_1}}} = 0.50 + 0.96\left( {\frac{{l_{\rm{a}}^{{\rm{cr}}}}}{d}} \right), $ |
| $ \sigma _{{{\rm{L}}_1}}^2 = {0.94^2}{\left( {\frac{{{\mu _{l_{\rm{a}}^0}}}}{{{\mu _{{d^0}}}}}} \right)^2}\left( {\delta _{l_{\rm{a}}^0}^2 + \delta _{{d^0}}^2} \right) = {0.076^2}{\left( {\frac{{l_{\rm{a}}^{{\rm{cr}}}}}{d}} \right)^2}, $ |
| $ {\delta _{{{\rm{L}}_1}}} = \frac{{{\sigma _{{{\rm{L}}_1}}}}}{{{\mu _{{{\rm{L}}_1}}}}} = \frac{{0.076\left( {l_{\rm{a}}^{{\rm{cr}}}/d} \right)}}{{0.50 + 0.96\left( {l_{\rm{a}}^{{\rm{cr}}}/d} \right)}}. $ |
考虑构件c、d尺寸偏差,T1的平均值、标准差和变异系数为:
| $ {\mu _{{{\rm{T}}_1}}} = 3.02 + 0.64\left( {\frac{c}{d}} \right), $ |
| $ \sigma _{{{\rm{T}}_1}}^2 = {0.71^2}{\left( {\frac{{{\mu _{{c^0}}}}}{{{\mu _{{d^0}}}}}} \right)^2}\left( {\delta _{{c^0}}^2 + \delta _{{d^0}}^2} \right) = {0.19^2}{\left( {\frac{c}{d}} \right)^2}, $ |
| $ {\delta _{{{\rm{T}}_1}}} = \frac{{{\sigma _{{{\rm{T}}_1}}}}}{{{\mu _{{{\rm{T}}_1}}}}} = \frac{{0.19\left( {c/d} \right)}}{{3.02 + 0.64\left( {c/d} \right)}}. $ |
按照最不利的情况进行分析,取c/d=1.则μT1=3.66,δT1=0.052.
灌浆料劈裂强度fts平均值为式(21),变异系数为式(22).
假设锚固抗力函数R服从对数正态分布,则由数理统计学[19]知识,抗力函数R的平均值、方差和变异系数分别为:
| $ {\mu _{\rm{R}}} = R\left( {{\mu _\Omega },{\mu _{{{\rm{L}}_1}}},{\mu _{{{\rm{T}}_1}}},{\mu _{{f_{{\rm{ts}}}}}}} \right), $ |
| $ \sigma _{\rm{R}}^2 = \sum\limits_{i = 1}^n {{{\left( {\frac{{\partial R}}{{\partial {x_i}}}} \right)}^2} \cdot \sigma _{{x_i}}^2} , $ |
| $ {\delta _{\rm{R}}} = \frac{{{\sigma _{\rm{R}}}}}{{{\mu _{\rm{R}}}}}. $ |
以上数据代入式(26),抗力R的统计参数为:
| $ {\mu _{\rm{R}}} = 4{\mu _\Omega } \cdot {\mu _{{{\rm{L}}_1}}} \cdot {\mu _{{{\rm{T}}_1}}} \cdot {\mu _{{f_{{\rm{ts}}}}}} = 58.09\left[ {0.50 + 0.96\left( {\frac{{l_{\rm{a}}^{{\rm{cr}}}}}{d}} \right)} \right], $ | (27) |
| $ \begin{array}{l} {\delta _{\rm{R}}} = \sqrt {\delta _\Omega ^2 + \delta _{{{\rm{L}}_1}}^2 + \delta _{{{\rm{T}}_1}}^2 + \delta _{{f_{{\rm{ts}}}}}^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\sqrt {0.022 + {{\left[ {\frac{{0.076\left( {{l_{\rm{a}}}/d} \right)}}{{0.50 + 0.96\left( {{l_{\rm{a}}}/d} \right)}}} \right]}^{\rm{2}}}} . \end{array} $ | (28) |
假设作用S亦服从对数正态分布,则设函数Z=lnR/S)=ln R-ln S,函数Z服从正态分布,其可靠指标可表示为
| $ \beta = \frac{{\ln {\mu _{\rm{R}}} - \ln {\mu _{\rm{S}}}}}{{\sqrt {\delta _{\rm{R}}^2 + \delta _{\rm{S}}^2} }}, $ | (29) |
则钢筋锚固长度的计算方程为
| $ \ln {\mu _{\rm{R}}} - \ln {\mu _{\rm{S}}} - \beta \sqrt {\delta _{\rm{R}}^2 + \delta _{\rm{S}}^2} = 0. $ | (30) |
式中:μS为式(19),δS为式(20),μR由式(27)计算得到,δR由式(28)计算得到.
考虑到实际中,灌浆料常被应用于建筑与公路结构,且钢筋发生锚固破坏的部位很可能在节点,故取锚固可靠度高于结构构件按照一般承载能力极限状态和正常使用极限状态设计时的可靠度指标[20].
建筑结构可靠度指标为β1=1.60,
公路桥梁结构可靠度指标为β2=1.94.
将式(19)、(20)、(27)、(28)和β1、β1分别代入式(30),可得建筑结构、公路桥梁结构的锚固长度分别为:
| $ {l_{{\rm{a1}}}} = 10.4d, $ |
| $ {l_{{\rm{a2}}}} = 11.1d. $ |
建筑结构钢筋锚固长度略小于公路桥梁结构,这是由两者不同的可靠度指标所决定的,为偏于安全考虑,对本试验灌浆料,锚固长度la=12d.
6.4 不同材料锚固长度对比GB 50010—2010《混凝土结构设计规范》[21]中规定,受拉钢筋的基本锚固长度为
| $ {l_{\rm{a}}} = \alpha \frac{{{f_{\rm{y}}}}}{{{f_{\rm{t}}}}}d, $ | (31) |
式中:d为锚固钢筋的直径,α为钢筋的外形系数,fy为钢筋抗拉强度设计值,ft为混凝土轴心抗拉强度设计值.带肋钢筋α取0.14, fy取实测钢筋屈服强度456 MPa,将灌浆料劈裂抗拉强度按ft=0.921fts换算得到轴心抗拉强度为3.58 MPa.将上述数据代入式(31)得la=17.8d.
山显彬[12]给出了带肋钢筋在自密实混凝土中钢筋锚固长度为
| $ {l_{\rm{a}}} = 0.102\frac{{{f_{\rm{y}}}}}{{{f_{\rm{t}}}}}d. $ |
本次试验的数据代入相关公式中,计算得到不同材料锚固长度见表 12.
| 表 12 不同材料锚固长度建议值对比 Table 12 Comparison of recommended values for anchorage length of different material |
可见,灌浆料的锚固长度与自密实混凝土相近,小于普通混凝土.
7 结论通过27个带肋钢筋-灌浆料拉拔试验,考察了保护层厚度、钢筋直径和锚固长度对试件的力学性能影响,得出以下结论:
1) 随着保护层厚度增大,试件所能承受的极限荷载不断增大,黏结强度也不断增大.相比于混凝土,保护层厚度增加相同幅度,灌浆料黏结强度增长慢.
2) 随着钢筋直径增大,极限荷载规律不明显,钢筋与灌浆料之间的黏结强度却不断降低.
3) 随着钢筋锚固长度的增加,试件所能承受的极限荷载不断增加,平均黏结应力却逐渐降低.相比于自密实混凝土,锚固长度增加相同幅度,灌浆料黏结强度增长快.
4) 分析了滑移发展过程,并给出典型的黏结-滑移曲线,曲线包含线性段、滑移加速段、下降段和残余段,拟合灌浆料黏结应力-滑移关系式.
5) 拟合了钢筋与灌浆料黏结强度公式,由于灌浆料不含粗骨料,砂浆强度比混凝土大,其与钢筋的黏结强度性能优于混凝土.
6) 拟合了黏结强度对应滑移值公式.由于灌浆料弹性模量较小,在相同应力下,肋间灌浆料变形比混凝土大,一定程度上造成钢筋与灌浆料之间的滑移量大于混凝土.
7) 提出了灌浆料与钢筋的锚固长度建议值,灌浆料的锚固长度与自密实混凝土相近,小于普通混凝土.
| [1] |
王建超, 周静海, 唐林. 钢筋-灌浆料黏结-滑移关系试验研究[J].
工业建筑, 2016, 46(S1): 627-630.
WANG Jianchao, ZHOU Jinghai, TANG Lin, et al. Experimental study on bond-slip relationship between rebar and grouting material[J]. Industrial Construction, 2016, 46(S1): 627-630. DOI: 10.13614/j.cnki.11-1962/tu.2015.05.001 |
| [2] |
PLOWMAN J M. The measurement of bond strength[J].
RILEM Symposium, Stockholm, 1957(5): 45-66.
|
| [3] |
ZUO J, DARWIN D. Bond strength of high relative rib area reinforcing bars[J].
Structural Engineering and Engineering Materials SM Report, 1998, 96(46): 630-641.
|
| [4] |
YERLICI V A, OZTURAN T. Factors affecting anchorage bond strength in high-performance concrete[J].
ACI Structural Journal, 2000, 97(3): 499-507.
|
| [5] |
KHEDER G F. Bond behavior for normal and high strength concrete[J].
Journal of Engineering and Development, 2005, 1(4): 99-119.
|
| [6] |
张海顺. 预制混凝土结构插入式预留孔灌浆钢筋锚固搭接试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
ZHANG Haishun. Experimental study on plug-in filling hole for lap-joint of steel bar of PC concrete structure[D].Harbin: Harbin Institute Technology, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10213-2010026455.htm |
| [7] |
国家质量技术监督局. 水泥胶砂强度检验方法: GB/T 17671—1999[S]. 北京: 中国建筑工业出版社, 1999.
The State Bureau of Quality and Technical Supervision: Method of testing cements-determination: GB/T 17671—1999[S].Beijing:China Building Industry Press, 1999. |
| [8] |
中华人民共和国建设部, 国家质量监督检验检疫总局. 普通混凝土力学性能试验方法标准: GB/T 50081—2002[S]. 北京: 中国建筑工业出版社, 2002.
Ministry of Constructure of the People's Republic of China, General Administration of Quality Supervision. Standard for test method of mechanical properties on ordinary concrete: GB/T 50081—2002[S].Beijing: China Building Industry Press, 2002. |
| [9] |
徐有邻, 沈文都, 汪洪. 钢筋砼粘结锚固性能的试验研究[J].
建筑结构学报, 1994, 15(3): 26-33.
XU Youlin, SHEN Wendu, WANG Hong. An Experimental study of bond-anchorage properties of bars in concrete[J]. Journal of Building Structures, 1994, 15(3): 26-33. |
| [10] |
王国杰. 高强度自密实混凝土及其与钢筋粘结锚固性能的试验研究[D]. 福州: 福州大学, 2002.
WANG Guojie. Experimental study on bond strength of high strength self-compacting concrete and steel bars[D].Fuzhou:Fuzhou University, 2002 http://cdmd.cnki.com.cn/Article/CDMD-10386-2002000131.htm |
| [11] |
尹健, 周士琼. 高性能混凝土轴心抗拉强度与劈裂抗拉强度试验研究[J].
长沙铁道学院学报, 2001, 19(2): 25-29.
YI Jian, ZHOU Shiqiong. A contrastive study on direct tensile strength and splitting tension strength of high performance concrete[J]. Journal of Changsha Railway University, 2001, 19(2): 25-29. DOI: 10.3969/j.issn.1672-7029.2001.02.005 |
| [12] |
山显彬. 变形钢筋与自密实混凝土之间粘结锚固性能试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.
SHAN Xianbin.Experimental research on bonding prop-erties between deformed bars and self-compacting concrete[D]. Harbin: Harbin Institute Technology, 2008 http://cdmd.cnki.com.cn/Article/CDMD-10213-2009291121.htm |
| [13] |
MIRIZA S M, HOUDE J. Study of bond stress-slip relationship in reinforced concrete[J].
Journal of the American Concrete Institute, 1979, 76(1): 19-46.
|
| [14] |
徐有邻. 变形钢筋-混凝土粘结锚固性能的试验研究[D]. 北京: 清华大学, 1990.
XU Youlin. Experimental study on bond behavior of deformed bar and concrete[D].Beijing:Tsinghua University, 1990. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jzjb403.004&dbname=CJFD&dbcode=CJFQ |
| [15] |
王冰, 李学章. 浮石混凝土与变形钢筋粘结锚固性能的研究[J].
哈尔滨建筑大学学报, 1998, 31(6): 30-37.
WANG Bing, LI Xuezhang. Experimental study on bond properties of deformed bars in pumice concrete[J]. Journal of Harbin University of Civil Engineering and Architecture, 1998, 31(6): 30-37. |
| [16] |
李渝军, 叶列平, 程志军, 等. 高强陶粒混凝土与变形钢筋粘结锚固强度的试验研究[J].
建筑科学, 2006, 22(4): 51-55.
LI Yujun, YE Lieping, CHENG Zhijun, et al. Bond strength between high-strength lightweight aggregate concrete and deformedbar[J]. Building Science, 2006, 22(4): 51-55. DOI: 10.13614/j.cnki.11-1962/tu.2006.04.013 |
| [17] |
贾方方. 钢筋与活性粉末混凝土粘结性能的试验研究[D]. 北京: 北京交通大学, 2013.
JIA Fangfang.Experimental study on bond propertied between steel bar and reactive powder concrete[D]. Beijing: Beijing Jiaotong University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10004-1013135863.htm |
| [18] |
欧阳煜, 赖校君. 高强钢筋高强混凝土粘结性能的试验与分析[J].
工业建筑, 2007, 37(5): 77-81.
OUYANG Yu, LAI Xiaojun. Experiment and analysis of bond performance between high-strength reinforcing bar and high-strength concrete[J]. Industrial Construction, 2007, 37(5): 77-81. DOI: 10.3321/j.issn:1000-8993.2007.05.020 |
| [19] |
龚光鲁.
概率论与数理统计[M]. 北京: 清华大学出版社, 2006: 177-178.
GONG Guanglu. Probability theory and mathematical statistics[M]. Beijing: Tshinghua University Press, 2006: 177-178. |
| [20] |
中华人民共和国建设部, 国家质量监督检验检疫总局. 建筑结构可靠度设计统一标准: GB 50068—2001[S]. 北京: 中国建筑工业出版社, 2001.
Ministry of Constructure of the People's Republic of China, General Administration of Quality Supervision.Unified standard for reliability design of building structures:GB 50068—2001[S].Beijing:China Building Ind-ustry Press, 2001 |
| [21] |
中华人民共和国建设部, 国家质量监督检验检疫总局. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010.
Ministry of Constructure of the People's Republic of China, General Administration of Quality Supervision. Code for design of concrete structures:GB 50010—2010[S].Beijing:China Building Industry Press, 2010. |
 2017, Vol. 49
2017, Vol. 49


