2. 同济大学 土木工程学院 地下建筑与工程系, 上海200092;
3. 江西基业科技有限公司, 南昌330200
2. Department of Geotechnical Engineering, College of Civil Engineering, Tongji University, Shanghai 200092, China;
3. Jiangxi Jiye Science and Technology Co., Ltd., Nanchang 330200, China
组合锤法是在强夯法基础上逐步完善后形成的一套新型地基处理技术[1].该技术对不同土质条件采用组合锤置换法和组合锤挤密法进行加固,其中组合锤置换法适用于处理饱和软土地基.组合锤置换法先用柱锤对需要处理的地基土冲击达到一定深度后,依据设计回填粗骨料,依次用中锤、扁锤夯实土体,最终形成上大下小的置换增强体[1].组合锤置换技术对普通强夯置换法和柱锤夯冲扩桩这两种处理方法从施工工艺和设备上进行了优化组合,弥补了各自技术上的缺陷.它与普通强夯置换法相比,具有锤底静压值和动压当量值大的特点,可以对较深的软土地基土进行加固处理.它与柱锤冲扩桩技术相比,优点有几方面:1)墩体直径从上到下变小,符合刚性荷载作用下基底附加应力传递规律;2)增大墩体直径,提高复合地基的置换率,从而提高复合地基承载力;3)墩体直径增大,缩短软土排水路径,加快墩间土体固结,从而提高墩体的围压约束力.因此,组合锤置换法拓宽了工程地质条件的适用领域和应用范围.
碎石、建筑垃圾等粗颗粒填充物形成了组合锤置换法的墩体,此为无粘结强度的散体材料墩.关于散体材料桩极限承载力的计算,目前最典型的是碎石桩,Brauns[2]、Wong[3]、龚晓南[4]、韩杰等[5]学者分别用极限平衡理论、被动土压力法、圆孔扩张理论、经验公式计算桩体极限承载力.由于组合锤置换法加固软土地基的施工工艺特殊,其与碎石桩不同,因此不能直接利用现有碎石桩极限承载力的计算成果,主要的区别表现在:置换墩墩体为变截面,利用Brauns[2]公式计算时墩体半径取值困难;利用Wong[3]公式计算时,不满足库伦被动土压力仅适用于无粘性土和朗肯被动土压力需墙背直立光滑的计算条件;圆孔扩张理论仅用于桩体为等截面的情况;经验公式对于组合锤置换墩来说也不适用.
本文开展了组合锤置换法室内模型试验,获得组合锤置换墩形态特征和破坏模式.基于此,采用能量法建立组合锤置换墩极限承载力计算模式,并根据GA_PSO优化算法计算了组合锤置换墩极限承载力.
1 置换墩单墩室内模型试验室内模型试验具有投资相对少、影响因素容易控制等优点[6],并且可直接揭示研究对象的某些特性.本试验旨在得到置换墩典型的墩体形态和刚性荷载作用下极限承载时的破坏模式,以此为置换墩极限承载力理论分析提供依据.
1.1 置换墩单墩形态模型试验试验模型箱大小为900 mm × 900 mm × 800 mm,模型与原型试验缩放比关系见表 1,表中β=12.5.所用淤泥质粉质黏土从试验区现场装箱,土性参数见表 2,夯前工作垫层采用粒径5~10 mm的碎石,厚度为30 mm,组合锤规格见表 3.
| 表 1 模型与原型的缩放比 Table 1 Reduced scale between model and prototype |
| 表 2 土层物理力学参数 Table 2 Physical and mechanical properites of soil layers |
| 表 3 组合锤规格 Table 3 Size of various hammers |
试验开始时,模型箱的底面和侧面关闭排水阀.夯击试验中,首先柱锤落距为100 cm,连续冲击地基土成孔,以提锤困难为停夯标准;填满夯坑,柱锤夯实填料;其次,中锤落距为100 cm,反复夯实,填满夯坑;最后,扁锤落距为100 cm,对浅层土体隆起及表层填料进行动力密实.置换墩形成后静置两天,采用挖掘技术(exhumation technique)获得置换墩[7-10],用水冲去墩体表层土可得完整的置换墩,它的典型形态见图 1.

|
图 1 典型置换墩墩体形态 Figure 1 Shape of typical replacement pier |
从图 1(a)、(b)可看出,置换墩体是一轴对称旋转体,其纵向剖面为一个上大下小的梯形截面.置换墩高度为h,柱锤夯击段高度为h3,中锤夯击段高度为h2,扁锤夯击段高度为h1,经统计,h3/h约为50%~60%,h2/h约为35%~40%,h1/h约为3%.因此,墩体形态主要由柱锤和中锤控制,扁锤对置换墩体形态的影响较小,主要起夯实地表的作用.
1.2 置换墩墩体破坏模式分析文献[11-13]用石膏成型法、水泥浆胶结法、直接切割法来研究载荷试验后碎石桩破坏模式.本文通过对比置换墩初始形态与极限承载变形后墩体的形态,同时监测在加载过程中墩体周围土体是否隆起,二者结合分析墩体破坏模式.墩体加载按静载试验按规范JGJ/T 290-2012进行,采用维持荷载法(图 2),至少分8级加载,当沉降急剧增大,荷载-沉降曲线出现陡降段时,停止加载.同时在墩周土体表面安放百分表,记录隆起土体变形.置换墩达到极限承载力后挖掘取样,用游标卡尺测量此时墩体的径向直径.试验时分3组进行,柱锤落距分别取v1=60 cm、v2=80 cm、v3=100 cm,中锤和扁锤取同一落距v=100 cm,置换墩加载前后形态对比图 3、4,墩体周围土体表面隆起变形测量见图 5.

|
图 2 置换墩室内静载荷试验 Figure 2 Indoor static load test of replacement pier |

|
图 3 置换墩加载前后形态对比 Figure 3 Shapes of replacement pier before and after load |
|
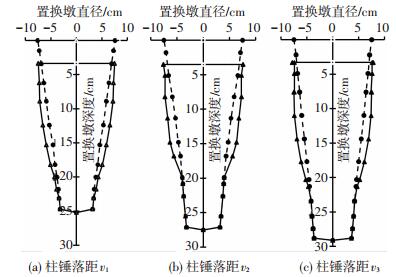
图 4 置换墩加载前后墩体径向变形对比 Figure 4 Radial deformation of replacement pier before and after load |

|
图 5 置换墩周表面土体隆起变形 Figure 5 Upheaval of surrounding soil around pier |
从图 3可直观看到墩体一定范围内受压鼓胀,经过对3组试验的墩体加载前后径向长度测量,从图 4可看出,在约2.0倍墩顶直径的深度范围内置换墩发生明显鼓胀变形,从图 5可看出,墩周土体表面发生隆起,隆起高度0.72~1.34 cm,且置换深度越浅,墩周土体表层隆起越大.因此,组合锤置换法在刚性荷载作用下极限承载时的破坏模式为鼓胀破坏.
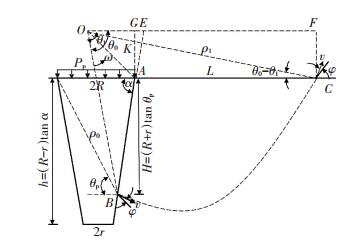
2 置换墩极限承载力计算 2.1 置换墩极限承载力理论模型置换墩为无粘结强度的散体材料,受竖向极限荷载作用时墩体鼓胀破坏,周围土体对墩体的侧向鼓胀产生径向约束力,计算模型简图见图 6.
|
图 6 组合锤置换墩鼓胀模型 Figure 6 Bulging failure mode of replacement pier |
鼓胀破坏段长度设为
| $ \begin{array}{*{20}{c}} {H = \left( {R + r} \right)\tan {\theta _{\rm{p}}},}\\ {{\theta _{\rm{p}}} = {{45}^ \circ } + {\varphi _{\rm{p}}}/2,aaaR = r,H = 2r\tan {\theta _{\rm{p}}}.} \end{array} $ [14-15] |
当墩周土体达到屈服应力时,土体即进入塑性流动状态服从流动法则,根据流动法则,土体塑性流动或者剪切滑动破坏时,滑动面上任一点的应变速度矢量v与该点处滑动线成φ角[16].
设墩周土体为对数螺线滑裂面且对数螺线中心点随滑动面变化而变化,其动径方程为ρθ=ρ0eθ tan φ,式中:φp为墩体材料的内摩擦角,θp为墩体破裂面与水平面的夹角,ρθ为ρ0绕对数螺线中心逆时针旋转角度θ角后的动径长度,φ为土体内摩擦角.
图 6中,对数螺线中心点O的位置随破裂面的变化而变化,因为置换墩的截面倾角α随组合锤径、墩体长度的不同而变化,ρ0和ρ1对应的θ0和θ1并不是定值,θ0和θ1的变化决定了土体被动破坏最危险滑动面.
图 6中,根据正弦定理:
| $ h = \left( {R - r} \right)\tan \alpha , $ | (1) |
| $ H = \left( {R + r} \right)\tan {\theta _{\rm{p}}}, $ | (2) |
| $ \frac{H}{{{\rho _0}}} = \sin {\theta _{\rm{0}}} - {{\rm{e}}^{{\theta _{\rm{1}}}\tan \varphi }}\sin \left( {{\theta _{\rm{0}}} - {\theta _{\rm{1}}}} \right), $ | (3) |
| $ \frac{L}{{{\rho _0}}} = \frac{{{{\rm{e}}^{{\theta _{\rm{1}}}\tan \varphi }}\sin \left( {{\theta _{\rm{0}}} - {\theta _{\rm{1}}} + \alpha } \right) - \sin \left( {{\theta _{\rm{0}}} + \alpha } \right)}}{{\sin \alpha }}. $ | (4) |
式中:R为中锤半径,r为柱锤半径,h为置换墩体高度,α为置换墩的截面倾角,ρ0为对数螺线在墩体破坏处旋入点到螺线中心点的长度.
下面用能量法建立单墩极限承载力表达式,分别对置换墩体、墩周土体进行受力分析,二者受力分析见图 7.

|
图 7 置换墩体和墩周土体受力分析 Figure 7 Force analysis of replacement pier and surrounding soil |
对于墩体,受荷载Pp作用和土体对墩体的极限约束力σru作用,利用库仑被动土压力理论计算得
| $ \begin{array}{*{20}{c}} {{P_{\rm{p}}} = {\sigma _{{\rm{ru}}}}{K_{\rm{p}}},}\\ {{K_{\rm{p}}} = \frac{{{{\sin }^2}\left( {\alpha - {\varphi _{\rm{p}}}} \right)}}{{{{\sin }^2}\alpha \sin \left( {\alpha + \delta } \right){{\left[ {1 - \sqrt {\frac{{\sin \left( {{\varphi _{\rm{p}}} + \delta } \right)\sin {\varphi _{\rm{p}}}}}{{\sin \left( {\alpha + \delta } \right)\sin \alpha }}} } \right]}^2}}}} \end{array}. $ | (5) |
式中:Kp为被动土压力系数,φp为墩体内摩擦角;δ为墩土间的摩擦角.
对于墩周土体,土体重力、沿对数螺线长度上消耗的摩擦力和墩体鼓胀作用三者所做功分别为W、W4和Wσ′ru,现分述如下:
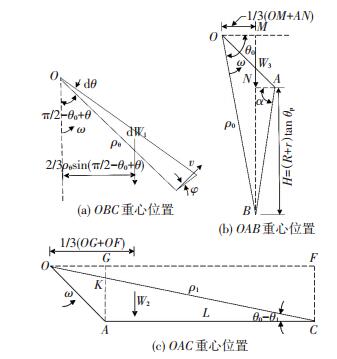
土体受重力的方向与其应变速率方向相反,重力做负功,W的大小可由W1、W2、W3叠加求出,W1、W2、W3分别表示OBC、OAC、OAB对转动中心O所做的功,其重心位置见图 8.
|
图 8 滑动体重力做功计算图 Figure 8 Calculation diagram of work done by sliding body due to gravity |
三者计算分别为:
| $ \begin{array}{*{20}{c}} {{\rm{d}}{W_1} = \omega \gamma \left[ {\frac{2}{3}{\rho _\theta }\sin \left( {\frac{\pi }{2} - {\theta _0} + \theta } \right)} \right]\left( {\frac{1}{2}{\rho _\theta }^2{\rm{d}}\theta } \right),}\\ {{W_1} = \frac{{\gamma \rho _0^3\omega }}{3}\int\limits_0^{{\theta _1}} {{{\rm{e}}^{3\theta \tan \varphi }}\cos \theta {\rm{d}}\theta = {f_1}\gamma \rho _0^3\omega ,} } \end{array} $ | (6) |
| $ {W_2} = {f_2}\gamma \rho _0^3\omega , $ | (7) |
| $ {W_3} = {f_3}\gamma \rho _0^3\omega , $ | (8) |
整理式(6)、(7)、(8)中的f1、f2、f3可得:
| $ \begin{array}{l} {f_1} = \frac{{{{\rm{e}}^{3{\theta _1}\tan \varphi }}\left[ {3\tan \varphi \cos \left( {{\theta _0} + {\theta _1}} \right) - \sin \left( {{\theta _0} - {\theta _1}} \right)} \right]}}{{3\left( {1 + 9{{\tan }^2}\varphi } \right)}} - \\ \;\;\;\;\;\;\frac{{3\tan \varphi \cos {\theta _0} + \sin {\theta _0}}}{{3\left( {1 + 9{{\tan }^2}\varphi } \right)}},\\ {f_2} = \frac{{{{\rm{e}}^{2{\theta _1}\tan \varphi }}\sin \left( {{\theta _0} - {\theta _1}} \right)}}{6} \cdot \frac{{\sin \left( {{\theta _1} + \alpha - {\theta _0}} \right) + \sin \left( {{\theta _0} + \alpha } \right)}}{{\sin \alpha }} \cdot \frac{L}{{{\rho _0}}},\\ {f_3} = \frac{{\sin {\theta _0}}}{6} \cdot \left[ {\frac{{\sin \left( {{\theta _0} + \alpha } \right) - {{\rm{e}}^{{\theta _1}\tan \varphi }}\sin \left( {{\theta _0} - {\theta _1}} \right)\cos \alpha }}{{\sin \alpha }} - } \right.\\ \;\;\;\;\;\;\left. {\frac{{{{\rm{e}}^{{\theta _1}\tan \varphi }}\sin \left( {{\theta _0} - {\theta _1}} \right)}}{{\tan {\theta _0}}}} \right] \cdot \left[ {{{\rm{e}}^{{\theta _1}\tan \varphi }}\sin \left( {{\theta _0} - {\theta _1}} \right) + \frac{H}{{{\rho _0}}}} \right] \cdot \\ \;\;\;\;\;\;\left( {2\cos {\theta _0} + \frac{1}{{\tan \alpha }} \cdot \frac{H}{{{\rho _0}}}} \right). \end{array} $ |
土体在塑性流动中的能量消散为cvcosφ[16].当滑动土体绕对数螺线中心产生角度ω时,可知沿对数螺线长度上内部消耗功W4为
| $ {W_4} = \int\limits_0^{{\theta _1}} {\frac{{c{\rho _\theta }v}}{{\cos \varphi }}\cos } \varphi {\rm{d}}\theta = \int\limits_0^{{\theta _1}} {c{\rho _\theta }v{\rm{d}}\theta = {f_4}c\rho _0^2\omega } , $ | (9) |
其中
置换墩鼓胀对土体作用力σ′ru(图 9),其作用点在AB边中点J点,当滑动土体绕对数螺线中心产生角度ω时,土体滑动平均速度为中点J点处的速度.土体受到的作用力σ′ru与J点处的速度夹角为π-θ0-α+θJ+δ,置换墩鼓胀对土体所做的功为Wσ′ru.

|
图 9 对数螺线滑动面计算图 Figure 9 Calculation diagram of log-spiral sliding plane |
Wσ′ru表示为
| $ {W_{{{\sigma '}_{{\rm{ru}}}}}} = {f_{{\sigma _{{\rm{ru}}}}}}{{\sigma '}_{{\rm{ru}}}}{\rho _0}\omega , $ | (10) |
其中
| $ {f_{{{\sigma '}_{{\rm{ru}}}}}} = \cos \left( {{\rm{\pi }} - {\theta _0} - \alpha + {\theta _{\rm{J}}} + \delta } \right){{\rm{e}}^{{\theta _{\rm{J}}}\tan \varphi }}, $ |
上式中θJ可根据下式计算:
| $ \overline {OJ} = \sqrt {\rho _0^2 + {{\overline {BJ} }^2} - 2{\rho _0}\overline {BJ} \cos \left( {{\rm{\pi }} - {\theta _0} - \alpha } \right).} $ | (11) |
在图 9中,由正弦定理可知:
| $ \frac{{\overline {OJ} }}{{\sin \left( {{\rm{\pi }} - {\theta _0} - \alpha } \right)}} = \frac{{\overline {BJ} }}{{\sin {\theta _{\rm{J}}}}}, $ | (12) |
将BJ=H/(2sinα)代入式(11)、(12),联立可得θJ:
| $ {\theta _{\rm{J}}} = {\sin ^{ - 1}}\left\{ {\frac{{\frac{{\sin \left( {{\theta _0} + \alpha } \right)}}{{2\sin \alpha }}}}{{\sqrt {{{\left( {\frac{{{\rho _0}}}{H}} \right)}^2} + \frac{1}{{4{{\sin }^2}\alpha }} - \frac{{{\rho _0}}}{H} \cdot \frac{{\cos \left( {{\theta _0} + \alpha } \right)}}{{\sin \alpha }}} }}} \right\}. $ |
根据能量理论,外力做功等于土体内部消耗的功,故有
| $ {W_{{{\sigma '}_{{\rm{ru}}}}}} - \left( {{W_1} - {W_2} - {W_3}} \right) = {W_4}. $ | (13) |
将式(6)、(7)、(8)、(9)代入式(13)得
| $ {{\sigma '}_{{\rm{ru}}}} = \frac{{\left( {{f_1} - {f_2} - {f_3}} \right)\gamma \rho _0^2 + {f_4}c{\rho _0}}}{{{f_{{{\sigma '}_{{\rm{ru}}}}}}}}. $ | (14) |
墩土相互作用力
| $ {{\sigma '}_{{\rm{ru}}}} = {\sigma _{{\rm{ru}}}}. $ | (15) |
将式(14)和式(15)代入式(5)得
| $ {P_{\rm{p}}} = \frac{{\left( {{f_1} - {f_2} - {f_3}} \right)\gamma \rho _0^2 + {f_4}c{\rho _0}}}{{{f_{{{\sigma '}_{{\rm{ru}}}}}}{K_{\rm{p}}}}}q\left( {{\theta _0},{\theta _1}} \right). $ | (16) |
如果式(16)中置换墩周土体被动破坏时σru取最小值,那么Pp也取到最小值,显然这是一个二元函数极值问题.对于式(16)极值求解,本文选取了GA_PSO优化算法[17-19],该算法通过在边界范围内搜索θ0和θ1来确定对数螺线最危险滑动面的中心位置O,进而计算出置换墩体极限承载力Pp,该算法的数学模型为:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathop{\rm minq}\nolimits} \left( \mathit{\Theta } \right) = \min q\left( {{\theta _0},{\theta _1}} \right),}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{h_1}\left( \mathit{\Theta } \right) = {\theta _0} > 0,}\\ {{h_2}\left( \mathit{\Theta } \right) = {\theta _1} > 0,}\\ {{h_3}\left( \mathit{\Theta } \right) = {\theta _1} - {\theta _0} < 0,}\\ {{h_4}\left( \mathit{\Theta } \right) = q\left( {{\theta _0},{\theta _1}} \right) > 0,}\\ {{h_5}\left( \mathit{\Theta } \right) = L\left( {{\theta _0},{\theta _1}} \right) > 0.} \end{array}} \right. $ | (17) |
式中:Θ为设计变量, q(Θ)为目标函数, hi(Θ)(i=1, 2, 3, 4, 5)为约束条件.
可见,该模型是一个含有复杂目标函数和约束条件的非线性规划问题,可用Matlab编程计算.
2.2 置换墩极限承载力影响因素分析为确定R、h、c、φ及δ对单墩极限承载力的影响,运用GA_PSO计算方法计算不同参数下的单墩极限承载力.R分别取0.8、1.0 m,h分别取3.5、4、5 m,r取0.4 m,φp取38°,γ取16.5 kN/m3,δ取2°、5°,对于软土c分别取5、10 kPa, φ分别取5°、10°,计算结果见表 4.把表 4中的数据绘制成更直观的图 10,从表 4及图 10可看出:

|
图 10 影响因素分析 Figure 10 Analysis of influence factors |
| 表 4 单墩极限承载力计算 Table 4 Calculation of ultimate bearing capacity of single pier |
1)在图 10(a)中,增加墩径对墩体极限承载力的影响显著,增加墩长对墩体极限承载力提高不明显.如墩长为5.0 m时,中锤半径从0.8 m增加到1.0 m,单墩极限承载力提高了约10%~20%.可见,扩大墩径可显著提高其承载力,这也是组合锤置换法的优势所在.
2)图 10(b)中,其他因素不变的情况下,墩土之间的内摩擦角增加,单墩极限承载力增加,但是增幅较小.如墩长为5 m时,墩土之间的内摩擦角从2°增加到5°,墩体极限承载力增加约0.5%~2%,如采用简化计算时,可不计墩土间的摩擦力.
3) 表 4可看出,其他因素不变情况下,随着周围土体粘聚力和内摩擦角增加,单墩极限承载力增加.
3 工程实例工程场地位于南昌市青山湖东,毗邻湖岸.勘察报告揭示的场地土层自上而下依次为:①淤泥质粉质黏土,流塑状,高压缩性,层厚1.2~4.6 m;②粉质黏土,可塑,中等压缩性,层厚5.5~6.9 m;③中砂,主要成分长石、石英,稍密~中密,颗粒级配较好,层厚5.3~7.3 m;以下岩土层略.场地地下水位稳定在1.0~3.5 m位置.场地的土性参数见表 5.
| 表 5 土层物理力学参数 Table 5 Physical and mechanical properites of soil layers in the field |
经验算,淤泥质粉质黏土层不满足地基承载力设计要求,采用组合锤置换法进行地基加固处理.组合锤选用柱锤半径为0.4 m、中锤半径为1.0 m、扁锤半径为1.2 m.施工前,在原地基表面铺设约2.4~3.0 m厚的回填土,回填土中粒径20~60 cm的块石约占70%.在组合锤施工工艺中,回填土作为工作垫层以保证强夯设备可以施工,同时也作为置换墩的墩体材料.回填土经组合锤夯击后,大部分已夯入淤泥质粉质黏土层中,墩体端部置于强度较好的粉质黏土持力层上,墩长约5 m.
初步设计时,应用GA_PSO算法计算墩体极限承载力,由于φp和δ这两个参数在工程现场较难获得,计算时依据工程经验及相关研究成果[20-22],φp取38°、δ取5°,把参数代入式(5),计算结果见表 6.
| 表 6 GA_PSO算法计算结果 Table 6 Calculation result based on GA_PSO method |
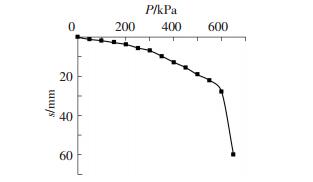
地基加固后进行单墩静载荷试验.由于置换墩体形态主要由柱锤和中锤控制,扁锤对置换墩体形态的影响较小,主要起夯实地表的作用.所以,综合考虑柱锤和中锤的底面积(柱锤和中锤平均面积为1.82 m2)和夯扩作用,确定载荷板为2.0 m2的圆形载荷板.将载荷板放置在置换墩顶面,采用维持荷载法分13级加载,直到墩体破坏,试验成果整理见表 7,试验p-s曲线见图 11.
| 表 7 静载荷试验成果 Table 7 Result of static load test |
|
图 11 静载荷试验P-s曲线 Figure 11 Curve of force-displacement obtained from static load test |
通过本文计算方法得到的置换墩极限承载力为571.4 kPa,现场静载荷试验实测值为600 kPa,计算结果略小于现场实测值,误差为4.7%.究其原因:一方面部分墩体参数取值来源于参考文献和工程经验;另一方面为了计算简便,没有考虑地表残留的薄层回填土对承载力的影响.但就工程的初步设计而言,置换墩极限承载力的计算值与实测值是比较接近的,为组合锤置换法工程初步设计提供了理论支持,也为组合锤置换法形成复合地基的承载力计算作出了有益探索.
4 结论1)根据模型试验,置换墩为一轴对称的旋转体,其纵向剖面是上大下小的梯形截面,柱锤夯击段高度约占墩体高度的50%~60%,中锤夯击段高度约占墩体高度的35%~40%,扁锤夯击段高度约占墩体高度的3%.
2)置换墩在刚性荷载作用下破坏模式为鼓胀破坏,鼓胀段长度约为墩顶直径的2.0倍,墩周土体有隆起,且置换深度越浅,墩周土体表层隆起越大.
3)中锤半径R增加,墩体承载力提高明显;增加墩长提高墩体极限承载力不明显;增加墩土间的摩擦力对于提高墩体承载力不明显,如采用简化计算时,可不计墩土间的摩擦力;墩周围土体粘聚力和内摩擦角增加,单墩极限承载力增加.
4)基于能量法建立单墩极限承载力计算模型并用GA_PSO算法计算,该计算值与实测值相比,二者较吻合,可用于工程的初步设计.
| [1] |
组合锤法地基处理技术规程:JGJ/T 290-2012[S].北京:中国建筑工业出版社, 2012.
Technical specification for ground treatment of combination hammer:JGJ/T 290-2012[S]. Beijing: China architecture and building press, 2012. http://industry.wanfangdata.com.cn/jz/Detail/Standard?id=Standard_JGJ%2FT%20290-2012&type=Free |
| [2] | BRAUNS J. Die anfangstraglast von schottersaulen im bindigen untergrund[J]. Die Bautechnik, 1978, 55 (8) : 263-271. |
| [3] | WONG H Y. Field instrumentation of vibroflotation foundation[J]. Field Instrumentation in Geotechnical Engineering, 1974, 23 (4) : 475-487. DOI: 10.1016/B978-0-408-70514-1.50039-1 |
| [4] |
龚晓南.
复合地基理论及工程应用[M]. 北京: 中国建筑工业出版社, 2002 .
GONG Xiaonan. Theory of composite foundation and engineering application[M]. Beijing: China Architecture and Building Press, 2002 . |
| [5] |
韩杰, 叶书麟, 曾志贤. 碎石桩加固沿海软土的试验研究[J].
工程勘察, 1990 (5) : 1-6.
HAN Jie. YE Shulin, ZENG Zhixian. Experimental study on coastal soft soil reinforced by sand columns[J]. Engineering Investigation and Survey, 1990 (5) : 1-6. |
| [6] |
徐挺.
相似理论与模型试验[M]. 北京: 中国农业机械出版社, 1982 .
XU Ting. Similarity theory and model test[M]. Beijing: China Agriculture and Machinery Press, 1982 . |
| [7] | WOOD D M, HU W, NASH D F T. Group effects in stone column foundation :model test[J]. Geotechnique, 2000, 50 (6) : 689-698. DOI: 10.1680/geot.2000.50.6.689 |
| [8] | AMBIL A P, GANDHI S R. Behaviour of stone cloumns based on experimental and FEM anylsis[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133 (4) : 405-415. DOI: 10.1061/(ASCE)1090-0241(2007)133:4(405) |
| [9] | ALI K, SHAHU J T, SHARMA K G.Behaviour of reinforced stone columns in soft soils: An experimental study[C]//Indian Geotechnical Conference.Mumbai.India:India Institue of Technology Bombay, 2010:625-628. |
| [10] | SHAHU J T, REDDY Y R. Clayey soil reinforced with stone column group: model tests and anysises[J]. Journal of Geotechnique and Geoenvironmental Engineering, 2011, 137 (12) : 1265-1274. DOI: 10.1061/(ASCE)GT.1943-5606.0000552 |
| [11] | DEB K, SAMADHIYA N K, NAMDEO J B. Laboratory model studies on unreinforced and geogrid-reinforced sand bed over stone column-improved soft clay[J]. Geotextiles and Geomenbranes, 2011, 29 (2) : 190-196. DOI: 10.1016/j.geotexmem.2010.06.004 |
| [12] | BLACK J A, SIVAKUMAR V, MADHAV M R, et al. Reinforced stone columns in weak deposits: laborary model study[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133 (9) : 1154-1161. DOI: 10.1061/(ASCE)1090-0241(2007)133:9(1154) |
| [13] | MCKELVEY D, SIVAKUMAR V, BELL A, et al. Modeling vibrated stone columns in soft clay[C]//Proceedings of the Institute of the Civil Engineers Geotechnical Engineering, 2004, 157(3):137-149. |
| [14] |
叶书麟.
地基处理与托换技术[M]. 北京: 中国建筑工业出版社, 1997 .
YE Shulin. Ground treatment and underpinning technology[M]. Beijing: China Architecture and Building Press, 1997 . |
| [15] |
叶观宝, 高彦斌.
地基处理[M]. 北京: 中国建筑工业出版社, 2009 .
YE Guanbao, GAO Yanbin. Ground treatment[M]. Beijing: China Architecture and Building Press, 2009 . |
| [16] |
顾慰慈.
挡土墙土压力计算手册[M]. 北京: 中国建材工业出版社, 2005 .
GU Weici. Calculation handbook of earth pressure against retaining wall[M]. Beijing: China Building Material Press, 2005 . |
| [17] |
玄光男, 程润伟.
遗传算法与工程优化[M]. 北京: 清华大学出版社, 2004 .
XUAN Guangnan, CHENG Runwei. Genetic algorithm and engineering optimization[M]. Beijing: Tsinghua University Press, 2004 . |
| [18] |
门朝光, 何忠政, 陈拥军, 等. 应用混合粒子群优化的检查点全局优化算法[J].
哈尔滨工业大学学报, 2015, 47 (5) : 91-96.
MEN Chaoguang, HE Zhongzheng, CHEN Yongjun, et al. The checkpoint global optimization algorithm based onthe mixed particle swarm optimization[J]. Journal of Harbin Institute of Technology, 2015, 47 (5) : 91-96. DOI: 10.11918/j.issn.0367-6234.2015.05.016 |
| [19] |
高飞.
Matlab智能算法超级学习手册[M]. 北京: 人民邮电出版社, 2014 .
GAO Fei. Super learning manual on Intelligent algorithm based on Matlab[M]. Beijing: Post & Telecom Press, 2014 . |
| [20] |
杨安顺, 冯晓腊, 张聪辰.
软土理论与工程[M]. 北京: 地质出版社, 2000 .
YANG Anshun, FENG Xiaola, ZHANG Congchen. Soft soil theory and engineering[M]. Beijing: Geology Publishing House, 2000 . |
| [21] |
雷和全.强夯块石墩复合地基理论与应用研究[D].湖南:湖南大学, 2006.
LEI Hequan. Theory and application study of the composite foundation formed by heavily rammed stone-piers[D].Hunan: Hunan University, 2006. http://www.cnki.com.cn/Article/CJFDTOTAL-GWGL200202010.htm |
| [22] |
刘杰.复合地基中垫层技术及桩土相互作用[D].湖南:中南大学, 2003.
LIU Jie. Cushion technique and interaction between reinforcements and surrounding soil in composite foundation[D]. Hunan: Central South University, 2003. http://www.cnki.com.cn/Article/CJFDTOTAL-XBJG200804009.htm |
 2017, Vol. 49
2017, Vol. 49


