中频电源可以分为旋转式和静止式,早期用旋转发电机产生的中频供电电源称之为旋转式,目前仍有部分场合在应用,但这种方式存在体积重量大、工作噪音大、发电效率比较低、能耗比较大、维护成本高等缺点.随着电力电子技术和功率开关器件的发展,静止式中频电源的发展已趋于成熟.但是,中频电源在相同的采样频率下一个周期内采样点是工频电源的1/8,控制精度大大降低,控制难度远大于工频50 Hz电源[1],因此中频电源优良精确的控制技术是该领域的重要研究方向之一.
传统的双闭环PI控制器结构简单[2],在直流电源及直流电机控制中得到了广泛的应用,但由内模原理[3]可知,这种控制方法在以正弦波为参考信号的单相交流电源控制中存在静差[4].文献[5]提出了一种复合控制控制策略,但重复控制的滞后特性使得闭环系统动态性能不高.文献[6]提出了基于准PR控制器的电压电流双闭环瞬时值控制策略,能够实现稳态性能,但PR控制器带宽较窄、对频率过于敏感,频率的偏移有可能导致系统不稳定,且不能消除不确定性参数对闭环系统性能的影响.
自1972年多伦多大学Davison教授首次提出鲁棒控制这个概念以来,鲁棒控制理论就得到了学者们的广泛关注和研究[7-8].鲁棒控制能对包含有界的不确定性系统进行调节校正,主要利用反馈-前馈输出状态关系来产生相应的控制输入,从而使系统输出沿预定“轨迹”变化.目前鲁棒控制理论已形成几个重要的分支,并建立了各自完备的理论体系,其中μ分析与综合方法在理论上不具有保守性,是鲁棒控制中比较优秀的控制策略,目前该方法在很多工程领域当中得到了应用[9-10],但是,μ分析与综合方法在中频电源中的应用未见报道.
本文主要研究的内容是将中频电源输出滤波器参数以及负载作为不确定性因素,使用结构奇异值理论来设计一个鲁棒控制器.首先分析单相中频电源的拓扑结构并建立了数学模型;然后对准PR控制器和鲁棒控制器作了简要介绍;最后借助于D-K迭代算法求解出鲁棒控制器,与双环准PR控制器进行对比分析,并对两种控制方法分别进行了软件仿真和实验验证.
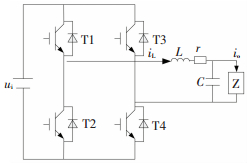
1 电路拓扑及建模分析本文论述的单相中频电源中采用H桥逆变结构,其电路拓扑如图 1所示,其中T1,T2,T3,T4为带有反并联二极管的功率器件IGBT,滤波器采用LC型滤波器,其中L为输出滤波电感,r为电感内阻,C为输出滤波电容. uo为中频电源输出电压,ui为直流母线电压,iL为滤波电感电流,io为输出负载电流.
|
图 1 单相中频电源拓扑结构 Figure 1 Circuit topology of single-phase medium frequency power supply |
H逆变桥可近似等效为一个比例环节k,将滤波电感电流iL(t),滤波电容电压uo(t) 为作为状态变量,输入变量为逆变桥输出kui,输出变量为电容电压uo(t),可以得到状态空间表达式为
| $ \left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\dot i}_{\rm{L}}}\left( t \right)} \\ {{{\dot u}_{\rm{o}}}\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{L}} & { - \frac{r}{L}} \\ 0 & {\frac{1}{C}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{\rm{L}}}\left( t \right)} \\ {{u_{\rm{o}}}\left( t \right)} \end{array}} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\frac{1}{L}} \\ 0 \end{array}} \right]k{u_{\rm{i}}} + \left[ {\begin{array}{*{20}{c}} 0 \\ { - \frac{1}{C}} \end{array}} \right]{i_{\rm{o}}}, \hfill \\ {u_{\rm{o}}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} 0 & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{\rm{L}}}\left( t \right)} \\ {{u_{\rm{o}}}\left( t \right)} \end{array}} \right]. \hfill \\ \end{array} \right. $ | (1) |
由状态空间模型可以得到单相中频电源的传递函数为
| $ {u_{\text{o}}}\left( s \right) = \frac{{kZ}}{{LCZ{s^2} + \left( {rCZ + L} \right)s + Z + r}}{u_{\text{i}}}\left( s \right). $ | (2) |
PR控制器自提出以来就成为了交流电源系统研究的热点,该控制器可以提高基波增益,有效地减小系统的跟踪误差,从而克服PI控制器的缺陷.为了对电源输出频率有一定的适应性,一般采用准PR控制器,其表达式为
| $ {G_{{\rm{PR}}}}\left( s \right) = {K_{\rm{p}}} + {K_{\rm{i}}}\frac{s}{{{s^2} + 2{\omega _{\rm{c}}}s + \omega _0^2}}. $ | (3) |
式中Kp为比例系数,Ki为谐振系数,对于400 Hz中频电源来说,其基波角频率ω0=800π.
准PR控制器在基波频率处有很高的增益,具有消除稳态误差的作用,但Ki的增大也使得准PR控制器的频带范围加大,进而增加了谐振的影响范围,不利于闭环系统稳定.关于准PR控制器的论述已经在诸多文献中提及,参考文献[11-12]中的设计方法最终确定双环准PR控制器参数为
| $ {G_{{\text{PR}}}}\left( s \right) = 3 + \frac{{1000s}}{{{s^2} + 20s + {{\left( {800\pi } \right)}^2}}}. $ | (4) |
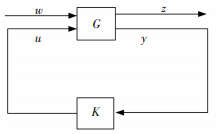
标准鲁棒控制问题的控制结构框图如图 2所示,图中w为外部输入的参考信号、干扰信号、以及传感器噪声信号等;z为跟踪误差、调节误差以及执行机构输出,是被控对象的输出信号;u为输入控制信号,y为输出信号,K为需要设计的鲁棒控制器,G为广义被控对象模型.
|
图 2 H∞标准问题控制结构图 Figure 2 Standard problem of robust control |
H∞控制的标准问题可以描述为:设计一个控制器u=Ky,使得闭环系统内稳定,并且使扰动输入w到控制输出z的传递函数Twz的H∞范数小于1,即
| $ {\left\| {{T_{wz}}} \right\|_\infty } < 1. $ | (5) |
结构化奇异值 (μ) 分析和综合方法是分析多重摄动条件下MIMO系统鲁棒稳定性和鲁棒性能的有力工具,在H∞控制问题分析时具有较小的保守性,为此,本文采用μ分析和综合方法来分析和设计中频电源的控制器.
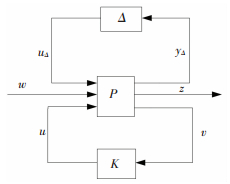
2.3 μ分析方法μ分析方法是把被控系统中所有不确定性摄动“提取”到一个对角型分块矩阵中,其中每一个对角元素代表某一个来源的不确定性,Δ =diag{Δi}(diag表示对角矩阵,Δi为系统的某一不确定量).如果把鲁棒控制器也提取出来,就得到了如图 3所示的不确定性系统一般结构框图.其中:P为广义标称对象, Δ为不确定性模块,K为鲁棒控制器;w为来自外界的扰动输入,z为信号输出. yΔ、uΔ分别为不确定模块的输入和输出,v、u分别为控制器的输入和输出[13].
|
图 3 不确定性系统的一般结构框图 Figure 3 General structure block diagram of uncertainty system |
利用μ分析控制问题时,可以把鲁棒控制器K视为另一个系统的一个元件,被吸收到互联结构中,假设广义标称对象和鲁棒控制器的传递函数为p和k,记M矩阵为
| $ \mathit{\boldsymbol{M}} = {F_1}\left( {p,k} \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{11}}} & {{\mathit{\boldsymbol{M}}_{12}}} \\ {{\mathit{\boldsymbol{M}}_{21}}} & {{\mathit{\boldsymbol{M}}_{22}}} \end{array}} \right]. $ | (6) |
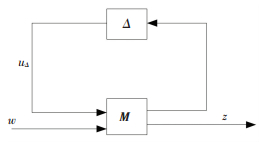
则不确定性系统的一般结构可以退化为如图 4所示的MΔ结构,其中
| $ z = \left[ {{\mathit{\boldsymbol{M}}_{22}} + {\mathit{\boldsymbol{M}}_{21}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{M}}_{11}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}} \right)}^{ - 1}}{\mathit{\boldsymbol{M}}_{12}}} \right]w = {F_u}\left( {\mathit{\boldsymbol{M}},\Delta } \right)\mathit{\boldsymbol{w}}\mathit{\boldsymbol{.}} $ | (7) |
|
图 4 MΔ结构 Figure 4 Structure of MΔ |
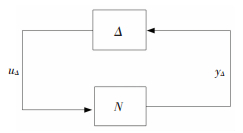
Fu(M, Δ) 实际反映了系统对输入干扰信号w的抑制作用,也就是系统的鲁棒性能.为了评价闭环系统的鲁棒稳定性以及鲁棒性能,将不确定系统分离成两个部分:不确定性Δ和广义被控对象N,得到如图 5所示的NΔ结构.图中N为稳定的传递函数,不确定性Δ ∈ Δ稳定并且满足‖Δ‖∞ < 1.如果闭环系统对所有的摄动是鲁棒稳定的,当且仅当
| $ \mathop {\sup }\limits_{\omega \in {\bf{R}}} {\mu _{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{\rm{p}}}}}\left( {\mathit{\boldsymbol{N}}\left( {{\rm{j}}\omega } \right)} \right) \leqslant 1 $ | (8) |
|
图 5 NΔ结构图 Figure 5 Structure diagram of NΔ |
成立即可.
将中频电源所带负载中的电阻、电感以及滤波电感作为系统模型的不确定因素Δ(s),可以得到
| $ \left\{ \begin{array}{l} {R_{\text{O}}} = \overline {{R_{\text{O}}}} \left( {1 + {P_{{R_{\text{O}}}}}{\delta _{{R_{\text{O}}}}}} \right), \hfill \\ {L_{\text{O}}} = \overline {{L_{\text{O}}}} \left( {1 + {P_{{L_{\text{O}}}}}{\delta _{{L_{\text{O}}}}}} \right), \hfill \\ L = \bar L\left( {1 + {P_1}{\delta _1}} \right). \hfill \\ \end{array} \right. $ | (9) |
式中:
| $ {M_{{R_{\text{O}}}}} = \left[ {\begin{array}{*{20}{c}} {0,\overline {{R_{\text{O}}}} } \\ {{P_{{R_{\text{O}}}}},\overline {{R_{\text{O}}}} } \end{array}} \right],{M_{{L_{\text{O}}}}} = \left[ {\begin{array}{*{20}{c}} { - {P_{{L_{\text{O}}}}},\frac{1}{{{L_{\text{O}}}}}} \\ { - {P_{{L_{\text{O}}}}},\frac{1}{{{L_{\text{O}}}}}} \end{array}} \right],{M_1} = \left[ {\begin{array}{*{20}{c}} { - {P_{{L_{\text{1}}}}},\frac{1}{{{L_{\text{1}}}}}} \\ { - {P_{{L_{\text{1}}}}},\frac{1}{{{L_{\text{1}}}}}} \end{array}} \right]. $ |
另外,为了使中频电源输出得到相应的动静态性能指标,可以通过选取适当的加权函数来实现.
2.4 加权函数WP的选取鲁棒控制器迫使被控系统的状态变量在稳态时变为0,从而形成0型控制系统.由内模原理可知,为使系统实现无静差控制和扰动抑制,必须在控制器中植入参考输入和扰动信号的模型,在稳态误差中就不包含这些频率分量.因为本文的控制对象为中频电源,参考输入和扰动信号均为400 Hz正弦波,其特征多项式的最小公倍数为s2+(800π)2.故选取灵敏度加权函数WP为
| $ {W_{\text{p}}} = \frac{{\omega _0^2}}{{{s^2} + \omega _0^2}}. $ |
其中ω0为所设计中频电源的基波角频率,ω0=800π.
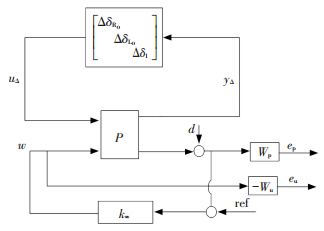
2.5 加权函数Wu的选取加权函数Wu的作用是防止鲁棒控制器输出饱和而添加的限制条件.结合回路成形理论,经过反复选择,最终得到Wu=0.001.综上,可以得到基于μ分析与综合方法的闭环系统控制框图如图 6所示.
|
图 6 闭环控制系统结构框图 Figure 6 Block diagram of the closed-loop system |
目前还没有一个直接的方法可以综合μ最优控制问题,然而,试图求取能够最小化给定μ条件的控制器,这就是μ综合问题.
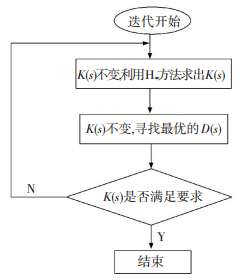
D-K迭代是求解μ综合问题比较好的方法,该方法结合了H∞分析和μ分析,通常能够取得不错的控制效果,其出发点是根据尺度变换后的奇异值给出μ的上界,D-K迭代流程图如图 7所示.
|
图 7 D-K迭代流程图 Figure 7 Block diagram of D-K iteration |
鲁棒控制工具箱提供了上述迭代过程的命令,dkit和dksyn都可以求取基于μ分析的鲁棒控制器,本文采用dksyn命令,经过7次迭代,才使得结构奇异值满足式 (9). 7次迭代结构奇异值分别为4.745,3.523,2.682,1.430,1.105,1.034,0.995,求得的控制器为6阶最优控制器.为了能够在DSP等数字处理芯片中实现该控制器,通过对控制器的降阶处理,最后得到的控制器为
| $ {K_\infty } = \frac{{{a_1}{s^4} + {b_1}{s^3} + {c_1}{s^2} + {d_1}s + {e_1}}}{{{s^4} + {f_1}{s^3} + {g_1}{s^2} + {h_1}s + {i_1}}}. $ |
其中:a1=1.208, b1=2 878, c1=1.193×109, d1=2.643×1012, e1=2.447×1014, f1=216, g1=9.932×108, h1=5.019×1010, i1 =6.167×1015.
通过Tustin方法将控制器K∞离散化为
| $ {K_\infty }\left( z \right) = \frac{{1.208{z^3} - 0.9149{z^2} - 1.188z + 0.8998}}{{{z^3} - 0.9413{z^2} - 0.922z + 0.9868}}. $ | (14) |
为了验证上述理论分析的正确性,利用MATLAB软件对全系统进行仿真分析,并在20 kW试验样机上进行了实验验证,其中电路参数为:输出滤波电容C=166 μF,滤波电感L=0.05 mH,阻性负载时Ro=0.67 Ω,阻感负载时Ro=0.67Ω,Lo=0.4 mH.
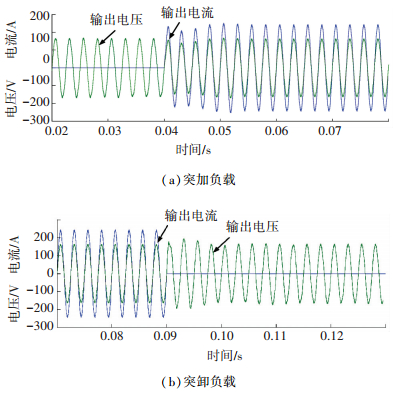
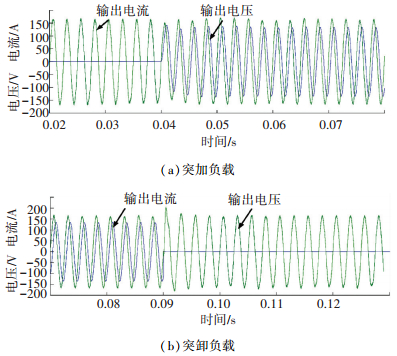
4.1 双环准PR控制器仿真验证图 8、9分别为带阻性负载和带阻感负载时,采用双环准PR控制器的单相中频电源输出电压电流仿真波形.
|
图 8 阻性负载时输出电压电流波形 Figure 8 Output voltage and current waveforms with resistive load |
|
图 9 阻感负载时输出电压电流波形 Figure 9 Output voltage and current waveforms with resistance-inductance load |
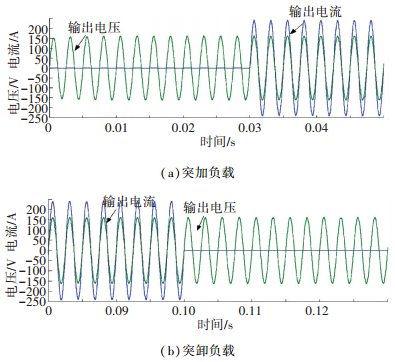
图 10、11分别为带阻性负载和带阻感负载时,采用鲁棒控制器的中频电源输出电压电流波形.
|
图 10 阻性负载时输出电压电流波形图 Figure 10 Output voltage and current waveforms with resistive load |
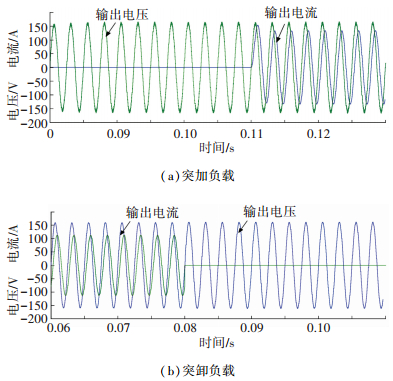
从上面的仿真结果可以看出,采用鲁棒控制器的中频电源系统,突加和突卸负载时输出电压波形几乎没有波动,比采用双环准PR控制器有更快的动态响应和抑制负载扰动能力.
|
图 11 阻感性负载时输出电压电流波形 Figure 11 Output voltage and current waveforms with resistance-inductance load |
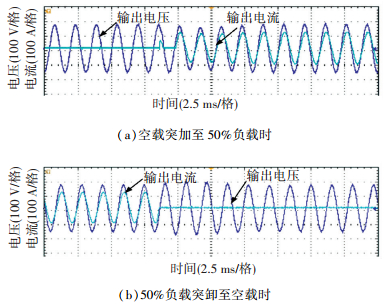
负载接50%负载 (10 kW) 纯阻性负载时和负载中串入电感0.4 mH,实验结果分别如图 12、13所示.负载接满载负载 (20 kW) 纯阻性负载时和负载中串入电感0.4 mH,实验结果分别如图 14、15所示.
|
图 12 阻性负载时电压电流实验波形 Figure 12 Experimental waveforms with with resistive load |
|
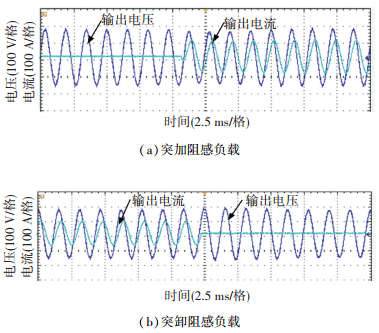
图 13 阻感负载时输出电压电流实验波形 Figure 13 Output voltage and current experimental waveforms with resistance-inductance load |
|
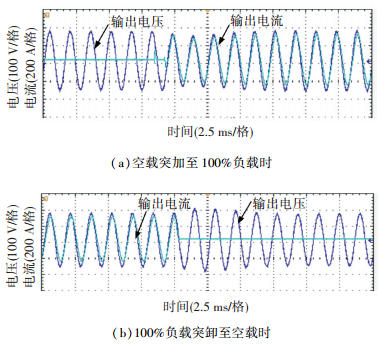
图 14 阻性负载时电压电流实验波形 Figure 14 Experimental waveforms with with resistive load |
|
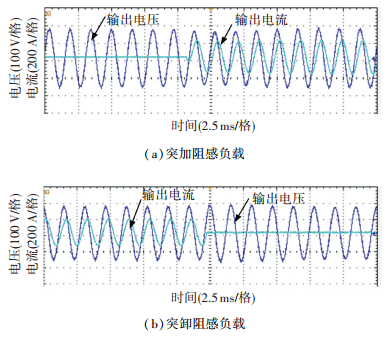
图 15 阻感负载时输出电压电流波形图 Figure 15 Output voltage and current experimental waveforms with resistance-inductance load |
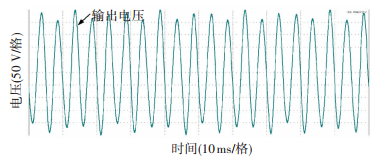
为了验证准PR控制器在频率偏移时的性能,当给定参考波频率为200 Hz时,输出电压产生了谐振,输出波形如图 16所示.
|
图 16 参考波频率为200 Hz时输出电压波形 Figure 16 Output voltage experimental waveforms of 200 Hz reference signal |
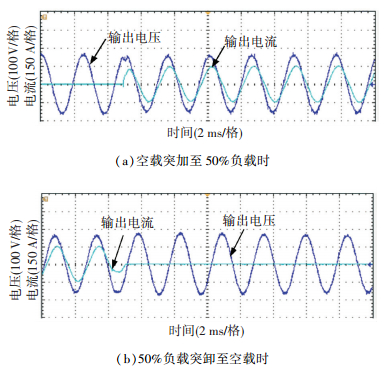
与双环准PR控制器采用相同的实验条件,50%负载和满载时实验结果分别如图 17~20所示.
|
图 17 阻性负载时电压电流实验波形 Figure 17 Experimental waveforms with with resistive load |
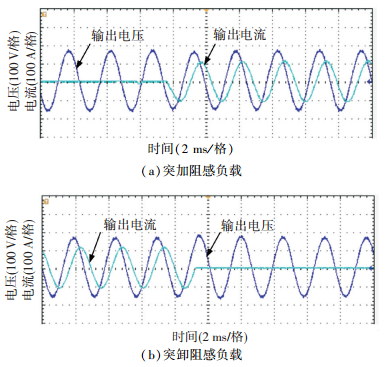
|
图 18 阻感负载时输出电压电流波形 Figure 18 Output voltage and current experimental waveforms with resistance-inductance load |
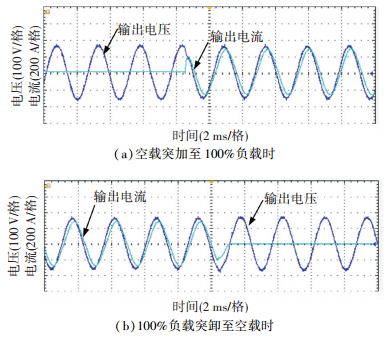
|
图 19 阻性负载时电压电流实验波形 Figure 19 Experimental waveforms with with resistive load |
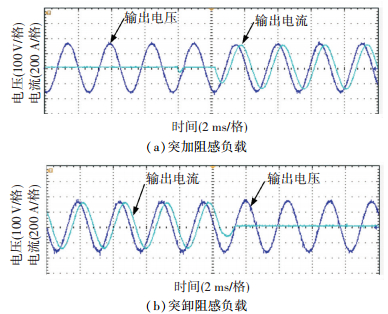
|
图 20 阻感负载时输出电压电流波形 Figure 20 Output voltage and current experimental waveforms with resistance-inductance load |
|
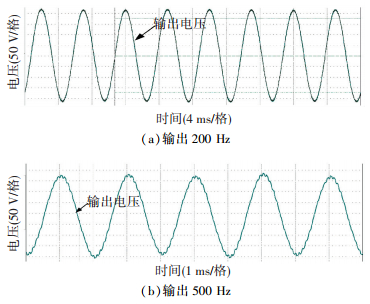
图 21 200、500 Hz输出电压波形 Figure 21 Output voltage experimental waveforms of 200 Hz and 500 Hz reference signal |
为了验证所设计的鲁棒控制器对频率的适应性,改变参考波频率,当参考波频率为200 Hz和500 Hz时,输出电压波形如图 21所示.
从上面结果可以得出采用双环准PR控制和单环鲁棒控制的中频电源动态性能,分别见表 1、2.
| 表 1 双环准PR控制时电源输出性能 Table 1 Output performance with double loop quasi PR control |
| 表 2 单环鲁棒控制时电源输出性能 Table 2 Output performance with single loop robust control |
表中Udown为突加负载电压跌落幅值,Uup为突卸负载电压超调幅值.从实验结果以及表 1、2可以看出,两种控制方法输出稳态电压都比较好,均能消除稳态误差,稳态电压波动为0.1 V,单环鲁棒控制器总谐波THD更小,电压波形质量比较高;在突加、突卸负载时,本文所设计的单环鲁棒控制器动态性能更好,突加负载电压跌落和突卸负载电压超调都非常小,表现出更加优良的动态性能.另外,当参考波频率为200、500 Hz时,鲁棒控制器仍能无静差跟踪,采用双环准PR控制器时产生了谐振而不能正常工作,说明所设计的控制器鲁棒性也比较好.
5 结论1) 所设计的鲁棒控制器仅用一个电压控制环就能达到系统的性能要求,控制结构简单,且跟踪性能及抑制干扰能力较强.
2) 闭环系统静态性能较好,稳态电压在114.9~115.1 V之间,且动态响应速度比双环准PR控制器更快,突加突卸10 kW负载动态恢复时间接近0 ms,突加突卸100%负载 (20 kW) 动态恢复时间在2.5 ms以内.
3) 另外采用鲁棒控制器时输出电压频率可以达到200~500 Hz,采用双环准PR控制时,参考波频率发生变化有可能产生谐振而不能正常工作,说明设计的鲁棒控制器表现出较强的鲁棒性能.
| [1] |
张银锋, 聂子玲, 朱俊杰. 基于二自由度有功/频率控制的中频逆变器并联系统仿真研究[J].
电器与能效管理技术, 2015, 13(1): 42-49.
ZHANG Yinfeng, NIE Ziling, ZHU Junjie. Research on parallel operation of medium frequency inverter based on two degree of freedom active power/frequency control[J]. Electrical & Energy Management Technology, 2015, 13(1): 42-49. |
| [2] |
陈斌, 裴忠才, 唐志勇. 液压四足机器人的自适应模糊PID控制[J].
哈尔滨工业大学学报, 2016, 48(9): 140-144.
CHEN Bin, PEI Zhongcai, TANG Zhiyong. Self-tuning fuzzy-PID control for hydraulic quadruped robot[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 140-144. DOI: 10.11918/j.issn.0367-6234.2016.09.024 |
| [3] | FRANCIS B A, WONHAM W M. The internal model principle incontrol theory[J]. IEEE Transactions on Power Electronics, 1976, 12(5): 457-465. |
| [4] | TIMBUS A, LISERRE M, TEODORESCU R. Evaluation of current controllers for distributed power generation systems[J]. IEEE Transactions on Power Electronics, 2009, 24(3): 654-664. DOI: 10.1109/TPEL.2009.2012527 |
| [5] |
刁元均, 邹滨. 基于复合控制的中频逆变电源研究流控制[J].
电力自动化设备, 2007, 27(7): 66-68.
DIAO Yuanjun, ZOU Bin. Hybrid control of medium frequency inverter[J]. Electric Power Automation Equipment, 2007, 27(7): 66-68. |
| [6] | ZHU Junjie, NIE Ziling, MA Weiming, et al. Dual-loop PR control for collapsed H-bridge single-phase 400 Hz power supply[C] //Asia-Pacific Power and Energy Engineering Conference. Shanghai: IEEE, 2012: 687-693. |
| [7] | 苏宏业. 鲁棒控制基础理论[M]. 北京: 科学出版社, 2010. |
| [8] | BABAZADEH M, KARIMI H. μ-synthesis control for an islanded microgrid[J]. IEEE Transactions on Power Electronics, 2011, 20(1): 1-6. |
| [9] |
鲍最, 冯勇, 孙黎霞. 非线性不确定系统的鲁棒滑模观测器设计[J].
哈尔滨工业大学学报, 2004, 36(5): 613-616.
BAO Sheng, FENG Yong, SUN Lixia. Robust sliding mode observer design of nonlinear uncertain systems[J]. Journal of Harbin Institute of Technology, 2004, 36(5): 613-616. |
| [10] |
贾庆贤, 张迎春, 李化义, 等. 卫星姿态控制系统鲁棒故障诊断方法[J].
哈尔滨工业大学学报, 2011, 43(3): 19-22.
JIA Qingxian, ZHANG Yingchun, LI Huayi. NUIO/LMI based robust fault diagnosis for satellite attitude control system[J]. Journal of Harbin Institute of Technology, 2011, 43(3): 19-22. DOI: 10.11918/j.issn.0367-6234.2011.03.004 |
| [11] | YAZDANI A, IRAVANI R. Voltage-sourced converters in power systems[M]. Hoboken: Wiley, 2010. |
| [12] | BACHA S, MUNTEANU I, BRATCU A I. Power electronic converters modeling and control[M]. Berlin: Springer, 2014. |
| [13] | SKOGESTAD S, POSTLETHWAITE I. Multivariable feedback control: analysis and design[M]. Hoboken: Wiley, 2005: 220-240. |
 2017, Vol. 49
2017, Vol. 49


