强风对于桥梁的行车舒适性和结构及行人的安全性都会造成不利的影响.对于跨江跨海峡的桥梁,桥面的侧向风速对行车安全性至关重要.风障作为改善桥面行车风环境的主要措施被广泛采用,如中国杭州湾大桥、香港青马大桥、法国Millau桥、英国Severn悬索桥、Queen Elizabeth二桥[1]和Severn二桥等[2]均加设了风障.目前对于风障形式的相关研究文献不足.为了阐述不同形式风障下,行车风环境的优劣,并探讨风障对于抗风性能的影响机制,本文以在建的秀山大桥其中的一个方案为研究背景,结合数值分析和风洞试验,对于风障形式进行了比选,并分析对比了有无风障时颤振性能及三分力系数的不同,最后通过二维三自由度方法研究了颤振驱动机制的变化.
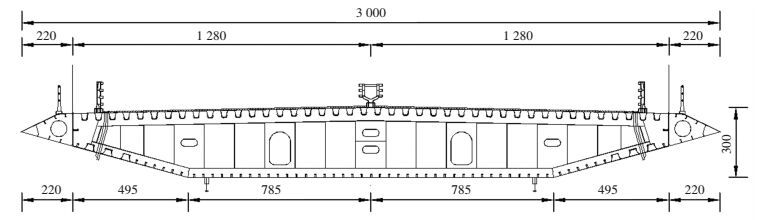
1 工程背景秀山大桥是浙江沿海舟山连岛工程的重要组成部分,建成后将连接官山岛和秀山岛[3].本文针对其在初步设计阶段的双塔三跨悬索桥方案开展研究,全桥跨径为264 m +918 m +365 m =1547 m,加劲梁为全宽30m的扁平流线型钢箱梁,梁高为3 m,断面形式如图 1.该桥桥址处为亚热带季风性海洋气候, 且舟山群岛受台风影响突出[4], 设计基本风速为44.5 m/s,成桥状态桥面高度基准风速为56.2 m/s;10 m高度处允许安全行车风速为25 m/s, 换算到桥面高度为31.7 m/s.
|
图 1 初始断面 (cm) Figure 1 Cross section of original bridge deck (cm) |
侧向风速控制标准是指为保证行车安全而规定的桥面等效风速的最大允许值,其具体取值与车辆本身的气动性能和行驶速度密切相关[5].
由于桥面以上风速的大小随着离开桥面的距离而变化,变化规律也因主梁断面和桥梁系构件不同而不同,为了衡量桥面侧向风速的大小,根据总风压相等的原则定义桥面等效风速为
| ${V_{{\rm{eff}}}} = \sqrt {\frac{1}{{{z_{\rm{r}}}}}\int_0^{{z_{\rm{r}}}} {{V^2}} \left( z \right){\rm{dz}}} .$ | (1) |
其中zr为等效范围,与车辆在桥面上行驶时受侧风影响的高度范围相对应.
受桥梁和桥面系构件的影响后,桥梁和桥面系构件具有挡风作用,使得桥面以上一定高度范围内的总风压小于桥梁上游来流的风压.因此,将桥面等效风速和基准高度风速的比值定义为侧风折减系数[6],即
| $\beta = \frac{{{V_{{\rm{eff}}}}}}{{{V_H}}}.$ | (2) |
其中VH为桥面以上1.5 m高度处的来流风速.
侧风折减系数受到两方面的影响,首先是结构的绕流引起风速的略增,同时边界层和栏杆作用使等效风速减小[7].
2.2 不同风障下风速剖面比较风障作为设置在主梁两侧的挡风构造物,是降低侧风影响的有效方法之一[8].风障形式的选取需要综合考虑建设成本,控制效果及美学等多方面因素.矩形断面由于加工方便,常为风障气动外形的首选,如在英国的赛文桥就采用了矩形的风障[8];而杭州湾跨海大桥[9]综合考虑了美学和材料成本,采用了C形的风障断面形式,其现场效果见图 2;宁波象山港大桥[10], 舟山的金塘桥[5]在考虑了美学因素之后将风障设计为椭圆曲线形.
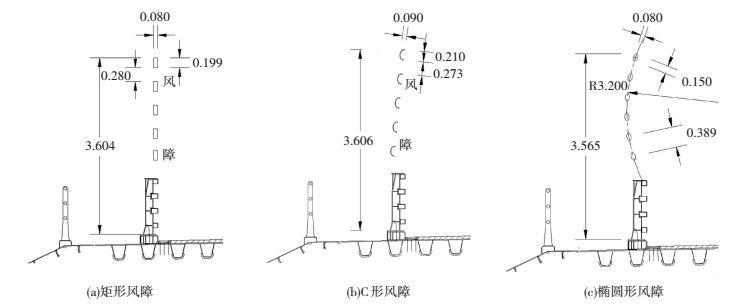
结合已有工程经验,研究初步考虑3种形式的风障,即矩形、C形和椭圆形,其断面形式及细部尺寸的选取见图 3,栏杆高度为1.2 m,风障和两侧防撞栏杆的总高度基本一致 (3.5~3.6 m).其中矩形风障和C形风障的阻塞面积相等,与总高度的比值为27.7%,椭圆形风障与总高度的比值略小,为24.9%.
|
图 3 风障局部尺寸示意 (m) Figure 3 Local dimensions of different wind barriers (m) |
计算流体力学方法 (CFD) 是一种研究流体流动等物理现象的现代技术,该方法可以直接模拟实际紊流风对桥梁断面的绕流现象[11]. CFD模拟主要借助于商业计算流体力学软件Fluent,计算过程中,综合网格量和计算能力的考虑,通过修改动粘性系数使得流场分析统一采用雷诺数Re=2×105(相对主梁宽度),基于k-ω SST湍流模型进行了二维RANS模拟,并结合Spalding率对壁面网格处的湍粘性进行了修正,取入口处的水平来流风速为U∞=10 m/s,模拟足够长的无量纲时间使得流场达到稳定.
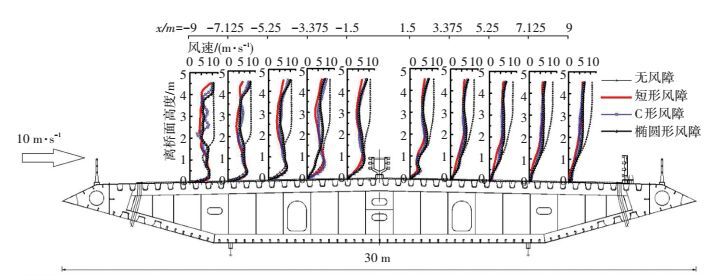
比较3种风障及无风障下计算平稳状态下,水平风速的统计平均值,得到图 4中的风速剖面.图中,x=0为桥面中心,x=-9为迎风侧第一根车道边缘,x =9为背风侧第一根车道边缘,可见:
|
图 4 基于CFD计算的桥面风速剖面 (m) Figure 4 Wind profile above deck by CFD (m) |
1) 添加风障后,能够有效地减小桥面上方5 m范围的风速,如在x=-1.5 m位置,4种工况下4.5 m高度处的风速依次为10.56、6.76、8.69、8.95 m/s,2.5 m高度处的风速依次为10.02、4.59、5.37、5.67 m/s.
2) 原始断面 (不设风障) 撇开两侧防撞栏杆和中央分隔栏杆的影响,当x>3.375 m时,风速随着离桥面的距离增加而单调递增,其剖面形状与规范中建议的e指数风速剖面接近. x ≤-3.375 m或0<x<3.375 m范围为栏杆影响区域,其风速剖面的特点为:在栏杆高度内 (左侧车行道h<1.2 m),风速随着高度h的增大先增大后减小,在中间h*高度处取得极大值,且h*的取值随着x的增大逐渐增大,如在x=-9 m时,h*≈0.352 m,当x=-5.25 m时,h*≈0.734 m,当x =-3.375时,h*≈1.038 m.而在与栏杆高度接近 (左侧车行道h≈1.2 m) 处,风速取得极小值.高度继续增加,风速转为单调递增.
3) 附加风障后,x=-9 m时风剖面受风障的形状影响较大.高度h<3.6 m时,风速剖面随着高度h呈现小幅波动的的趋势:对于C形风障,栏杆高度范围内 (h<1.2 m) 和风障高度范围 (1.2 m<h<3.6 m) 的平均风速接近,在6 m/s上下;对于矩形和椭圆形风障,栏杆高度范围内 (h<1.2 m) 的风速略大于风障高度范围 (1.2 m<h<3.6 m) 的平均风速,如对于矩形断面,h<1.2 m时,风速为8 m/s,而1.2 m<h<3.6 m,风速仅为5 m/s左右. x ≥-7.125 m时,风障形状对于风速的影响较小,3种情况下风速剖面形状接近.特别是在-7.125 m≤x≤-1.5 m时,风速随着高度h先增大后减小再增加,风剖面底部的极大值对应的高度h*随着x增大而增大,风速极小值对应的高度略低于风障上缘的高度 (3.6 m).当x≥7.125 m时,风速剖面接近e指数剖面.
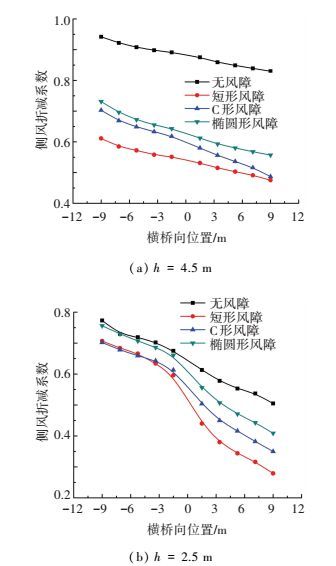
2.3 不同风障侧风折减系数比较根据2.1节中定义的侧风折减系数计算得到4种工况在不同横向位置处的侧风折减系数,针对集装箱卡车 (4.5 m) 和小轿车 (2.5 m) 的高度[5]统计得到侧风折减系数如下图 5.
|
图 5 横桥向侧风折减系数变化规律 Figure 5 Variation of cross wind reduction coefficients |
原始断面由于桥面自身边界层的存在,沿着横桥向也存在侧风的折减效应,越靠近背风侧 (x越大),边界层越厚,侧风折减系数最大.集装箱卡车高度处,由于接近桥面自身边界层的边界层高度,侧风折减效应明显比h=2.5 m (小轿车高度) 时弱,如x=9 m, h=4.5 m时,侧风折减系数为0.83,而h=2.5 m时,侧风折减系数达到0.505.
设置风障后,侧风的折减效应加强,对于h=4.5 m的情况,侧风折减系数在0.5~0.75之间.特别是矩形风障:当x=-9 m时 (迎风侧第1根车道边缘),侧风折减系数为0.558,远小于无风障时的0.83;当x=9 m (背风侧第一根车道边缘) 时,侧风折减系数为0.475.对于小轿车高度:当x<-1.5 m时,由于落在防撞栏杆引起的边界层高度范围内,侧向折减系数较无风障时减小不明显;当x>1.5 m时,侧风折减效应明显加强,特别是矩形断面风障,x=9 m时,侧风折减系数达到0.279,远小于无风障时的0.505.
比较3种形式风障,从侧向风折减的角度考虑,矩形风障的折减效应最明显,分析其主要原因,该断面自身较钝,绕流时矩形表面形成较厚的边界层,从而使得尾流影响区域风速小于C形和椭圆形.
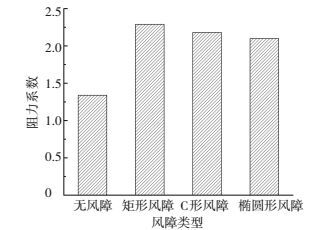
2.4 不同风障阻力系数比较横风向阻力是桥梁结构设计中需要考虑的活载.如阻力过大,可能引起桥梁结构静风作用下整体失稳的问题.故有必要比较不同形状的风障的阻力系数,比较结果如图 6所示.
|
图 6 基于CFD的阻力系数比较 Figure 6 Comparison of drag coefficients by CFD |
由图 6可知,相比于没有风障的情况,附加风障后断面的挡风面积明显增大,阻力系数也随着增大.根据二维CFD计算,阻力系数从无风障时的1.34上升到超过2.参考如图 3所示的风障局部尺寸图,C形风障和矩形风障的挡风面积相当,而C形风障的阻力系数明显小于矩形风障,侧向荷载增加较少. C形风障和椭圆形风障的阻力系数相差约4%,与挡风面积相差的比例相当,椭圆形风障的阻力较小.
3 基于风洞试验的颤振性能比较本研究参照浙江省高速公路管理的有关风速标准,取桥面侧向风速控制标准为25 m/s.即当桥址处10 m高度位置、10 min平均风速不超过25 m/s时,秀山大桥所有行车道位置的桥面等效风速不得超过25 m/s (此时桥面高度处风速为31.7 m/s).据此,秀山大桥跨中的容许侧风折减系数为25/31.7= 0.79,即采用3种形式的风障都能满足要求.综合考虑,采用阻力系数较小的椭圆形风障和无风障的原始断面作进一步的风致动力稳定性能比较.
3.1 风洞试验概述刚体节段模型的颤振试验在同济大学土木工程防灾国家重点实验室TJ-2号风洞中完成.该风洞试验段的几何尺寸为高2.5 m,宽3.0 m,长15 m,风洞试验风速范围为0~68 m/s.
根据桥梁实际主梁断面尺寸,风洞的条件和试验的要求, 节段模型设计的几何相似比为λL=1:60.节段模型的材料主要采用金属框架提供刚度,三夹板模拟主梁的气动外形,另外采用ABS塑料模拟防撞栏杆等附属措施,从而保证桥面几何外形的相似性[12].
颤振实验由于其振型间的耦合作用,因此需要严格保证模型的竖扭频率比相似[13],对应风速比为λU=1:4.5.具体设计参数见表 1.
| 表 1 节段模型颤振实验参数 Table 1 Experimental parameters of sectional model |
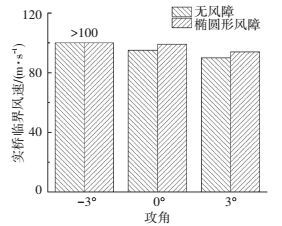
节段模型颤振实验在-3°,0°,3° 3个风攻角的均匀流场中进行.分别开展了原始断面和加椭圆形风障的颤振实验,椭圆形风障模型如图 7,得到3个攻角下的颤振临界风速如图 8所示.

|
图 7 椭圆形风障模型 Figure 7 Test model of ellipse-shaped wind barrier |
|
图 8 试验颤振临界风速比较 Figure 8 Comparison of critical flutter speed |
在-3°攻角下,试验中由于静风位移过大未测到颤振发散现象,考虑到该攻角非最不利攻角,因此不作进一步研究.对于0°和3°攻角,通过添加椭圆形的风障,颤振临界风速不但没有因为挡风面积增大而降低,反而有了小幅度的提高,如0°攻角下,原断面的颤振临界风速为95 m/s,附加椭圆形风障后,颤振临界风速增大到99 m/s.对于两种断面,最不利攻角均为3°.
3.3 实测静力三分力系数比较静风荷载常是大跨桥梁设计中的控制荷载,而静力三分力系数随着风攻角的变化趋势是静风稳定性分析、建立抖振力的拟静力理论的基础[14],因此有必要比较设置椭圆形风障前后静力三分力系数的变化规律.
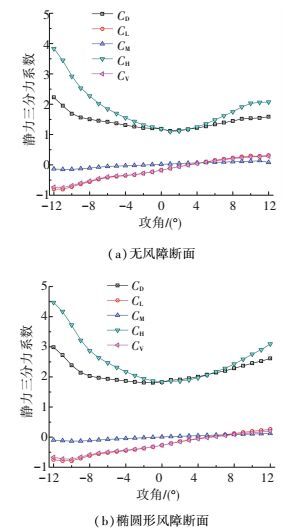
节段模型测力实验在均匀流场中进行,分别测试原始断面和附加椭圆形风障断面在-12°~12°之间,每个1°攻角下阻力、升力和升力矩曲线的变化规律.得到两种断面的静力三分力系数比较结果如图 9所示.
|
图 9 两种断面的实测静力三分力系数 Figure 9 Three-component force coefficients of two sections by wind tunnel test |
CD、CL对应风轴下的阻力和升力系数取值,CH、CV对应体轴,两者通过坐标变换可以相互转化,故只比较风轴下的三分力系数取值.其定义为
| $\left\{ {\begin{array}{*{20}{l}} {{C_{\rm{D}}} = \frac{{{F_{\rm{D}}}}}{{\frac{1}{2}\rho {U^2}H}},}\\ {{C_{\rm{L}}} = \frac{{{F_{\rm{L}}}}}{{\frac{1}{2}\rho {U^2}B}},}\\ {{C_{\rm{M}}} = \frac{{{M_{\rm{L}}}}}{{\frac{1}{2}\rho {U^2}{B^2}}}.} \end{array}.} \right.$ |
设置椭圆形风障前后,升力系数CL和升力矩系数CM基本没有变化.后者数值保持在-0.15~0.15之间,且在攻角为-10°时分别取到最小值-0.15和-0.13,此后随着攻角的增加缓慢变大.升力系数的变化趋势类似,两种断面的升力系数均在-0.8~0.3之间,且在-10°时取到极小值-0.81和-0.79.
对比有无风障的断面,阻力系数CD的变化明显,其总体趋势随着攻角的变化先减小后增大,对于原始断面,在1°取到最小值1.12,在-12°取到最大值2.23.在附加椭圆形风障后,最小值为1.81,对应攻角为-1°,最大值为2.99,对应攻角为-12°.
相比于图 6所示的CFD计算结果,0°攻角下的阻力系数实测值总体偏大了0.2,但总体趋势一致,其原因需作进一步分析.
4 颤振发散机理比较根据二维三自由度耦合颤振[15]分析结果,本文试验的工况都是系统的扭转运动发散导致的颤振失稳现象.因此,为阐明颤振驱动机理,有必要进一步分析系统扭转运动阻尼的变化规律.
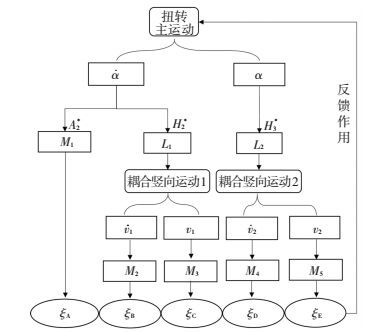
如图 10所示,根据二维三自由度耦合颤振分析方法 (2d-3DOF)[16]的原理,系统扭转主运动可以分为速度项α·和位移项
|
图 10 二维三自由度阻尼 (比) 图解 Figure 10 Diagram of damping ratio in 2d-3DOF method |
对于扭转位移α项,其与颤振导数H3*结合,可产生作用于桥面的升力L2项,该升力作用在桥梁断面,同样可激发出耦合竖向运动.两部分的耦合竖向运动又可分解为速度分量和位移分量,分别与颤振导数A1*和A4*项对应,得到耦合气动升力矩M2、M3、M4、M5,并反馈给扭转主运动.
因此,按照激励-反馈原理,与上述M1、M2、M3、M4、M5对应,系统的扭转气动阻尼 (比) 共有5种产生途径,记为ξA、ξB、ξC、ξD、ξE项,即[17]
| $\left\{ \begin{array}{*{35}{l}} {{\xi }_{\text{A}}}=-\frac{\rho {{B}^{4}}}{2I}\cdot A_{2}^{*}, \\ {{\xi }_{\text{B}}}=-\frac{{{\rho }^{2}}{{B}^{6}}}{2{{m}_{h}}I}\cdot {{\Omega }_{\alpha h}}\cdot A_{1}^{*}H_{2}^{*}\text{cos}{{\theta }_{1}}, \\ {{\xi }_{\text{C}}}=\frac{{{\rho }^{2}}{{B}^{6}}}{2{{m}_{h}}I}\cdot {{\Omega }_{\alpha h}}\cdot A_{4}^{*}H_{2}^{*}\text{sin}{{\theta }_{1}}, \\ {{\xi }_{\text{D}}}=-\frac{{{\rho }^{2}}{{B}^{6}}}{2{{m}_{h}}I}\cdot {{\Omega }_{\alpha h}}\cdot A_{1}^{*}H_{3}^{*}\text{cos}{{\theta }_{2}}, \\ {{\xi }_{\text{E}}}=\frac{{{\rho }^{2}}{{B}^{6}}}{2{{m}_{h}}I}\cdot {{\Omega }_{\alpha h}}\cdot A_{4}^{*}H_{3}^{*}\text{sin}{{\theta }_{2}}. \\ \end{array} \right.$ | (3) |
式中Ωαh为无量纲系数.
图 11、12分别给出了应用二维三自由度耦合颤振分析方法计算得到的两种比较断面系统扭转运动气动阻尼比各项随风速增加变化规律.分析图中的数据可得以下规律:
|
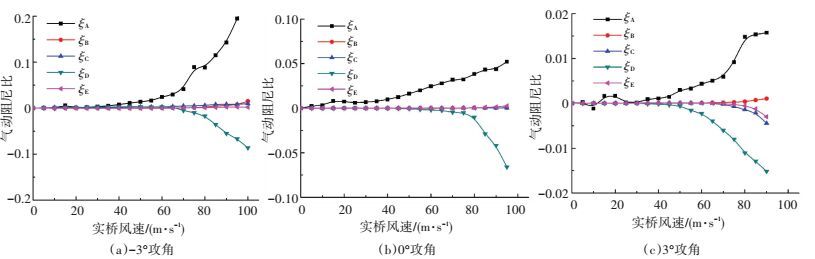
图 11 不同攻角下原始断面的气动阻尼比较 Figure 11 Aerodynamic damping of the original section |
|
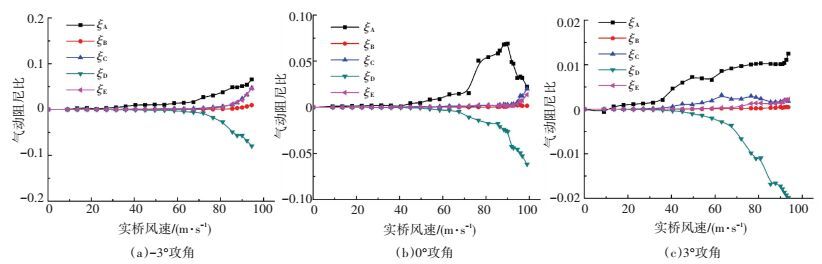
图 12 最优断面的气动阻尼比较 Figure 12 Aerodynamic damping of the optimal section |
1)-3°攻角下,由于试验中未观测到颤振发散,因此总阻尼比仍保持正值,但两种断面气动阻尼比的组成不同. ξD项均是主要的负阻尼项,可以预见该项将是驱动颤振的主要力量,也是导致系统发散的主要原因.当实际风速为90 m/s时,原始断面ξD项气动阻尼为-0.055,而带风障断面为-0.057,较前者更为不利.对于正阻尼的贡献,原始断面主要来自于气动阻尼ξA项,对应扭转运动自身产生的气动阻尼,其随着风速单调增大,在实际风速为90 m/s时到达0.143,而此时带风障断面的ξA项气动阻尼只有0.051.两种断面的气动阻尼比ξB、ξC、ξE项区别明显,对于原始断面,三项阻尼比取值保持在0附近,但在加了椭圆形风障后,三项取值随着风速保持正值且单调增大.特别是ξC、ξE项,在90 m/s时分别达到0.024和0.020(原始断面为0.008和0.002).由于这三项气动阻尼比的变化规律,使得在90 m/s时,虽然ξA项正阻尼要小于原始断面,但总的阻尼比仍能维持在正值.
2) 对于0°攻角下,原始断面起到主导作用的仍为气动正阻尼比ξA项和气动负阻尼比ξD项,两者的绝对值随着风速保持单调递增.在95 m/s时,原始断面ξA项为0.052,ξD项为-0.066,各项合计气动阻尼比为-1.06%,绝对值大于结构阻尼0.5%,结构发散.而对于加风障断面,ξA项随着风速先增大后减小,在风速为90 m/s时取最大值为0.069,在95 m/s时为0.032.需要指出的是,ξC、ξE项气动阻尼比在高风速 (>90 m/s) 突然增大,95 m/s时达到0.006和0.004.由于这两项的贡献,95 m/s时的气动总阻尼为-0.23%,绝对值小于结构阻尼,结构未发散,与试验结果吻合.
3) +3°攻角为断面颤振性能的控制攻角.原始断面气动阻尼比ξA项保持正值且随着风速单调递增,在90 m/s时达到0.016. ξB项保持较小值. ξC、ξD、ξE项表现为单调负阻尼,在90 m/s时分别达到-0.004、-0.015和-0.003. 90 m/s是五项合计气动阻尼为-0.58%,绝对值大于结构阻尼比,结构发散.而对于附加了椭圆形风障后的断面,ξA项阻尼随风速的增长较缓,90 m/s仅为0.010,但ξB、ξC、ξE项阻尼均为正值,分别为0.001、0.002和0.002. ξD项阻尼仍为系统发散的主要原因,其绝对值随风速单调递增,在90 m/s时达到-0.017,此时合计五项气动阻尼为-0.35%,绝对值小于结构阻尼,结构未发散,与试验结果吻合.
4) 综合3个攻角下的颤振驱动机理,对于两种断面,ξA项气动阻尼比始终为结构的稳定因素,ξD项始终为不稳定因素.在0°攻角时,设置椭圆形风障后ξA项的变化趋势明显改变.同时,相比于原始断面,ξB、ξC、ξE项阻尼比不但没有激发结构的发散,还在高风速区体现为较大的正值,视为椭圆形风障提高颤振临界风速的主要原因.
5 结论1) 设置风障显著地改变了横桥向各点的风速剖面,除栏杆影响区域,其余位置风速剖面由原始断面的“近e指数”分布变为了先增后减再增的非单调分布.风障能有效的增加桥面侧风折减效应,4.5 m高度处的折减效果尤为明显,矩形风障折减效果最优,C形次之,原始断面最差.相应原始断面阻力系数最小,矩形风障最大.
2) 节段模型测振试验发现,设置了椭圆形风障后不但没有恶化断面的抗风性能,对于颤振临界风速还有微弱的提高.通过测力试验,椭圆形风障对于升力和升力矩系数的影响不明显,但能明显增大侧向的阻力系数,在零度攻角下,由1.187变为1.827,涨幅达到53.9%.
3) 基于二维三自由度颤振,理论分析得到的颤振发散风速能与试验值较好吻合.附加风障后,气动阻尼比ξB、ξC、ξE项由原始断面的较小值 (甚至为负值) 变为较为可观的正值,是颤振临界风速能提高的主要原因,同时0°攻角下ξA项气动阻尼的变化规律发生了明显的变化.
4) 综合行车风环境和颤振稳定性的考虑,认为椭圆形风障是同类设计中可选的风障形式.
| [1] | OSTENFELD K H. Great belt link: the east bridge[J]. Concrete International, 1992, 14(12): 643-643. |
| [2] |
陈晓冬. 大跨桥梁侧风行车安全分析[D]. 上海: 同济大学, 2007.
CHEN Xiaodong. Vehicle safety analysis of long-span bridge under cross wind [D].Shanghai: Tongji University, 2007. |
| [3] |
葛耀君, 杨詠昕. 官山至秀山公路秀山大桥初步设计阶段抗风性能研究[R]. 上海: 土木工程防灾国家重点实验室 (同济大学), 2014.
GE Yaojun, YANG Yonxing. Investigation on wind resistant performance of Xiushan Bridge in preliminary design stage[R]. Shanghai: State Key Laboratory of Disaster Reduction in Civil Engineering (Tongji University), 2014. |
| [4] |
张文明, 杨詠昕, 葛耀君, 等. 风障对大跨度悬索桥抗风性能的影响[J].
武汉理工大学学报, 2008, 30(11): 113-116.
ZHANG Wenming, YANG Yongxin, GE Yaojun, et al. , Effects of wind barrier on wind-resistant performance of long-span suspension bridge[J]. Journal of Wuhan University of Technology, 2008, 30(11): 113-116. |
| [5] |
汪正华. 桥面行车风环境评价与侧风行车安全控制研究[D]. 上海: 同济大学, 2010.
WANG Zhenghua. Evaluation of wind environment on bridge deck and research on security control of cross wind safety of automobiles[D]. Shanghai: Tongji University, 2010. |
| [6] |
庞加斌, 王达磊, 陈艾荣, 等. 桥面侧风对行车安全性影响的概率评价方法[J].
中国公路学报, 2006, 19(4): 59-64.
PANG Jiabin, WANG Dalei, CHEN Airong, et al. Probability evaluating method of bridge deck side wind effects on driving safety[J]. China Journal of Highway and Transport, 2006, 19(4): 59-64. DOI: 10.3321/j.issn:1001-7372.2006.04.011 |
| [7] |
阮欣, 陈艾荣, 王达磊. 杭州湾跨海大桥风障设置风险评估[J].
桥梁建设, 2007(1): 78-80.
RUAN Xin, CHEN Airong, WANG Dalei. Risk assessment of installing of wind shielding screens for Hangzhou bay sea-crossing bridge[J]. Bridge Construction, 2007(1): 78-80. DOI: 10.3969/j.issn.1003-4722.2007.01.021 |
| [8] |
罗晓瑜, 陈艾荣, 王达磊. 杭州湾跨海大桥风障造型美学思考[C]//第十七届全国桥梁学术会议论文集. 北京: 人民交通出版社, 2006: 360-365.
LUO Xiaoyu, CHEN Airong, WANG Dalei. Aesthetic thinking of Hangzhou bay bridge's wind barrier[C]// Proceedings of 17th National Bridge Academic Conference. Beijing:China Communications Press, 2006:360-365. |
| [9] |
程国政. 杭州湾大桥的"驯风师"-记我校桥梁系杭州湾大桥灾害性天气对策课题组[N]. 同济大学校报, 2008-05-10(2).
CHENG Guozheng. Wind master of Hangzhou Bay Bridge[N]. School newspaper of Tongji University, 2008-05-10(2). |
| [10] |
周奇, 朱乐东, 郭震山. 桥梁曲线风障减风效果的数值模拟[C]//第十四届全国结构风工程学术会议论文集. 北京: 中国土木工程学会桥梁与结构工程分会, 2009: 944-951.
ZHOU Qi, ZHU Ledong, GUO Zhenshan. Numerical simulation of wind reduction effect for curve wind barrier on bridge[C]// Proceedings of 14th National Conference on Structural Wind Engineering. Beijing: Bridge and Structural Engineering Branch of China Civil Engineering Society, 2009: 944-951. |
| [11] | LI Ke, GE Yaojun, GUO Zengwei, et al. Theoretical framework of feedback aerodynamic control of flutter oscillation for long-span suspension bridges by the twin-winglet system[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2015, 145(1): 166-177. DOI: 10.1016/j.jweia.2015.06.012 |
| [12] |
张文明, 葛耀君. 双主跨悬索桥颤振节段模型试验模态匹配问题[J].
哈尔滨工业大学学报, 2013, 45(12): 90-93.
ZHANG Wenming, GE Yaojun. Mode matching problem of sectional model flutter tests for a suspension bridge with double main spans[J]. Journal of Harbin Institute of Technology, 2013, 45(12): 90-93. DOI: 10.11918/j.issn.0367-6234.2013.12.016 |
| [13] |
钱国伟, 曹丰产, 葛耀君. Π型叠合梁斜拉桥涡振性能及气动控制措施研究[J].
振动与冲击, 2015, 34(2): 176-181.
QIAN Guowei, CAO Fengchan, GE Yaojun. Vortex-induced vibration performance of a cable-stayed bridge with π shaped composite deck and its aerodynamic control measures[J]. Journal of Vibration and Shock, 2015, 34(2): 176-181. DOI: 10.13465/j.cnki.jvs.2015.02.031 |
| [14] |
陈政清.
桥梁风工程[M]. 北京: 人民交通出版社, 2005: 59.
CHEN Zhengqing. Bridge wind engineering[M]. Beijing: China Communications Press, 2005: 59. |
| [15] |
项海帆.
现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005: 206-226.
XIANG Haifan. Modern theory and practice on bridge wind resistance[M]. Beijing: China Communications Press, 2005: 206-226. |
| [16] |
杨詠昕, 葛耀君, 项海帆. 大跨度桥梁中央开槽颤振控制效果和机理研究[J].
土木工程学报, 2006, 39(7): 74-80.
YANG Yongxin, GE Yaojun, XIANG Haifan. Flutter control effect and mechanism of central-slotting for long-span bridges[J]. China Civil Engineering Journal, 2006, 39(7): 74-80. DOI: 10.3321/j.issn:1000-131X.2006.07.013 |
| [17] | YANG Yongxin, GE Yaojun, XIANG Haifan, et al. Investigation on flutter mechanism of long-span bridges with 2d-3DOF method[J]. Wind & Structures An International Journal, 2007, 10(5): 421-435. |
 2017, Vol. 49
2017, Vol. 49



