航空金属结构在服役过程中会出现各种形式的损伤,其中以裂纹和腐蚀最为严重.若不能及时发现这些损伤,将会严重影响飞行器的飞行安全.利用结构健康监测技术可以实时监测结构的健康状态,及时发现损伤的存在,避免灾难的发生.Lamb波对损伤较为敏感,并且还可以发展成像技术将损伤的位置显示出来.因此,利用Lamb波技术识别损伤成为当前结构健康监测领域的热点之一.偏移法[1-2]、时间反转法[3]、相控阵法[4]等成像方法利用信号的传播时间,对损伤进行定位,进而利用成像算法对损伤进行成像.但是Lamb波的多模态转换以及弥散特性增加了精确提取Lamb波损伤信号传播时间的难度.为了保证提取到的Lamb波损伤信号传播时间的精度,需要运用小波变换[5-6]、Hilbert-Huang变换[7-8]等时频分析方法对信号进行处理.为避免提取损伤信号传播时间带来的复杂信号处理方法,Hay等[9-10]在传统CT成像的基础上,提出了一种基于损伤存在概率的成像算法,称为RAPID (reconstruction algorithm for probabilistic inspection of damage).该方法通过比较结构损伤前后的Lamb波信号的相关系数得到一组损伤指标 (damage index,DI) 来评估损伤存在的概率,然后对损伤进行快速、准确成像.但是该方法使用等长度的信号段参与计算相关系数,得到的损伤指标也与信号段的长度有关.信号段长度较短时,可能只包含较少的有效信号;信号段长度较长时,可能包含了较多的无关信号.信号段长度过短或过长都会影响着基于信号相关系数计算的损伤指标,将有可能出现损伤识别虚假和识别不明显的现象.
本文提出了一种有效信号段自提取算法来识别多损伤的方法.先将待检测结构进行区域分割,然后根据压电传感器间的距离和Lamb波的波速,自动计算并提取出接收传感器接收到的有效信号段.利用提取出的有效信号段计算基于信号相关系数的损伤指标,最后利用RAPID算法将损伤的位置成像出来.本文提出的有效信号段自提取算法克服了等长度信号段参与多损伤成像可能带来的识别不准确的缺点.铝板实验结果验证了所提方法在多损伤成像中应用的可行性和有效性.
1 有效信号段自提取算法在激励传感器激励出Lamb波时,接收传感器便同时开始接收信号.但是,Lamb波从激励到被接收,有一段在结构中传播的时间,这段时间理论上表现在接收信号中就是一段幅值为0的信号段.由于实际环境中噪声、信号干扰的影响,实际这段信号的幅值通常不为0.但信号噪声通常频率相对较低,Lamb波为高频激励信号,可以通过滤波去除噪声.这个信号段在计算信号相关系数时因为不携带任何与结构有关的信息,可以被认为是无关信号.同理,Lamb波传播到边界或者其他传感器时,Lamb波的模态会发生转变,甚至出现信号混叠等现象,较为复杂,难以处理.因此这段信号对于计算信号相关系数是不利的,也是无关的.所以,实际的有效信号段就是在检测范围内,从接收传感器接收到Lamb波到接收传感器接收完Lamb波的这段信号.也就是接收传感器在采集时间内采集到的信号去掉无关信号后,截取出来的信号.这段有效信号包含了Lamb波在无损结构中传播的信号和结构遇到损伤时的散射信号.
当以较短的信号段参与损伤指标的计算时,距离激励传感器较远的接收传感器接收到的信号中可能会缺失一部分有效信号;若以较长的信号段参与损伤指标的计算,距离激励传感器较近的接收传感器接收到的信号中可能会包含较多的无关信号.因此,信号段长度过短或者过长都不利于基于信号相关系数的损伤指标的计算.信号中携带结构损伤信息的有效信号越多,得出的信号相关系数就越有效,损伤指标也就越准确.接收传感器在接收到Lamb波之前采集到的信号和从边界反射回来的信号都属于无关信号,这种无关信号越少,对损伤指标的不利影响也就越小.采用等长度信号段来得到损伤指标时,改变信号段的长度,就会改变参与计算的信号段中的有效信号段和无关信号段的长度,使得基于信号相关系数的损伤指标发生改变,损伤识别结果中将有可能出现损伤识别虚假和识别不明显的现象.针对等长度信号段参与计算的不足,提出了一种有效信号段自提取的算法.
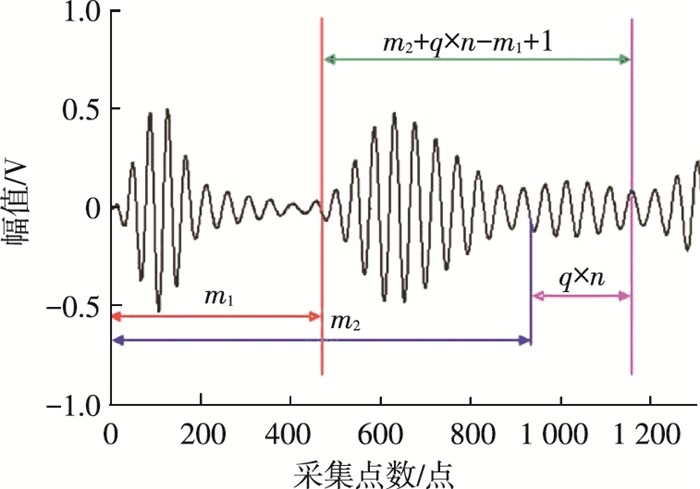
该有效信号段自提取算法的提取关键参数就是接收传感器接收到Lamb波的时刻和完全接收完不包括边界和其他传感器反射的Lamb波的时刻.因此在传感器布置时,应考虑传感器之间的距离和传感器与边界的距离,即要求速度最快的S0波从激励传感器出发,经边界或相邻传感器反射到接收传感器所需的时间尽可能地多于速度最慢的A0波从出发到接收完全所需要的时间.根据Lamb波在结构的传播速度,结合压电传感器之间的距离,计算速度最快的S0波从出发到刚接收所需要的时间,转化为相对应的信号采集点数m1,计算速度最慢的A0波从出发到刚接收所需要的时间,转化为相对应的信号采集点数m2,并补偿Lamb波的波宽长度对应的信号采集点数n,为减小误差,乘以一个放大倍数q.对采集到的信号进行截断处理,提取出有效信号段.提取过程如下:从信号段第m1个点数作为起点,从信号段第 (m2+q×n) 个点数作为终点,起点至终点的这段信号段就是有效信号段,有效信号段长度num=m2+q×n-m1+1,如图 1所示.
|
图 1 有效信号段的提取 Figure 1 Extraction of effective signal |
由于Lamb波信号经过结构损伤时发生散射和能量衰减,信号幅值会发生明显的改变,通过比较结构在发生损伤前后的Lamb波信号,就能确定幅值的变化量,进而判断出结构中是否存在损伤[11-12].另一种处理方法则是对Lamb波信号进行时频分析,把时域内的Lamb波信号转换为频域或者时频域内的特征进行分析,提取出的幅值变化量就作为损伤因子[13-14].本文利用损伤发生前后的信号幅值的相关系数作为损伤的判断依据来判断损识别伤和损伤成像.
某条路径采集到的损伤前后的信号段经截断处理后分别用a和b表示,ρ表示信号a和b的相关系数,对于离散信号,ρ可表示为
| $ \rho = \frac{{\sum\limits_{j = 1}^{{\rm{num}}} {\left( {{a_j} - \bar a} \right)\left( {{b_j} - \bar b} \right)} }}{{\sqrt {\sum\limits_{j = 1}^{{\rm{num}}} {{{\left( {{a_j} - \bar a} \right)}^2}} \sum\limits_{j = 1}^{{\rm{num}}} {{{\left( {{b_j} - \bar b} \right)}^2}} } }}. $ |
式中:a、b分别为信号a、b的均值; aj、bj分别为a、b的第j个值; num为有效信号段的长度.损伤指标DI则定义为
| $ {\rm{DI = 1}} - \left| \rho \right|. $ | (1) |
因此DI的数值越大,则该路径损伤前后的信号相关性越小,损伤位置范围就越大.
3 损伤成像算法在RAPID成像算法基础上,引进图像增强因子以提高损伤区域与无损伤区域的对比度.然后根据每个激励-接收路径的损伤指标,计算整个结构内每个像素点存在损伤的概率叠加.
| $ P\left( {x,y} \right) = {\left\{ {\sum\limits_{i = 1}^n {{p_i}\left( {x,y} \right)} } \right\}^\alpha } = {\left\{ {\sum\limits_{i = 1}^n {{\rm{D}}{{\rm{I}}_i}\frac{{\beta - {R_i}}}{{\beta - 1}}} } \right\}^\alpha }. $ |
式中:P (x, y) 为像素点 (x, y) 存在损伤的概率;n为激励-接收路径的数目;pi(x, y) 为由第i条激励-接收路径计算所得到的在像素点 (x, y) 存在损伤的概率;DIi为按照式 (1) 计算得到的第i条激励-接收路径的损伤指标;β为控制激励-接收路径影响范围的尺度因子,大小为椭圆离心率的倒数,该椭圆是以激励和接收信号的压电传感器作为两个焦点;α为图像增强因子,可以提高损伤区域与无损伤区域的对比度.
| $ {R_i} = \left\{ \begin{array}{l} {\rm{R}}{{\rm{D}}_i},{\rm{R}}{{\rm{D}}_i} < \beta ;\\ \beta ,{\rm{R}}{{\rm{D}}_i} > \beta . \end{array} \right. $ |
式中RDi为像素点 (x, y) 到第i条激励-接收路径的激励点和接收点距离之和与激励点到接收点距离的比值.
| $ {\rm{R}}{{\rm{D}}_i} = \frac{{\sqrt {{{\left( {x - {x_{ai}}} \right)}^2} + {{\left( {y - {y_{ai}}} \right)}^2}} + \sqrt {{{\left( {x - {x_{si}}} \right)}^2} + {{\left( {y - {y_{si}}} \right)}^2}} }}{{\sqrt {{{\left( {{x_{ai}} - {x_{si}}} \right)}^2} + {{\left( {{y_{ai}} - {y_{si}}} \right)}^2}} }}. $ | (2) |
式中:下标ai为激励压电传感器; 下标si为接收压电传感器.
图 2为激励-接收路径示意图,当像素点 (x, y) 落在椭圆内时,Ri由式 (2) 计算得到.当像素点落在椭圆外时,此时Ri=β,主要考虑直接路径上的损伤.

|
图 2 激励-接收路径示意 Figure 2 Schematic diagram of actuator-receiver sensing path |
当激励-接收路径距离损伤较近时,该路径计算得出的损伤指标DI就会较大,距离越远的则越小.由于环境的影响,在不存在损伤的路径上,损伤发生前后采集到的信号也存在较小差异,使得DI较小,而靠近损伤的路径的DI则会很大.算法以DI的最大值的0.2倍为阈值,低于阈值的认为该路径距离损伤较远,将该路径的DI置为0.用这种方法对先前计算的DI进行修正,然后将修正后的DI用于损伤成像算法的计算.
4 实验验证 4.1 实验布置基于Lamb波的结构健康监测方法可以应用于大型金属板状结构范围广、距离长的损伤监测[15-16].根据结构的大小,可以布置M行N列的传感器阵列,将较大的检测区域分割成若干子区域.一个子区域就是一个基本检测单元,在基本检测单元内对损伤进行检测和识别.在本文的研究中,以2行3列共6个压电传感器组成的区域作为一个独立的基本检测单元.
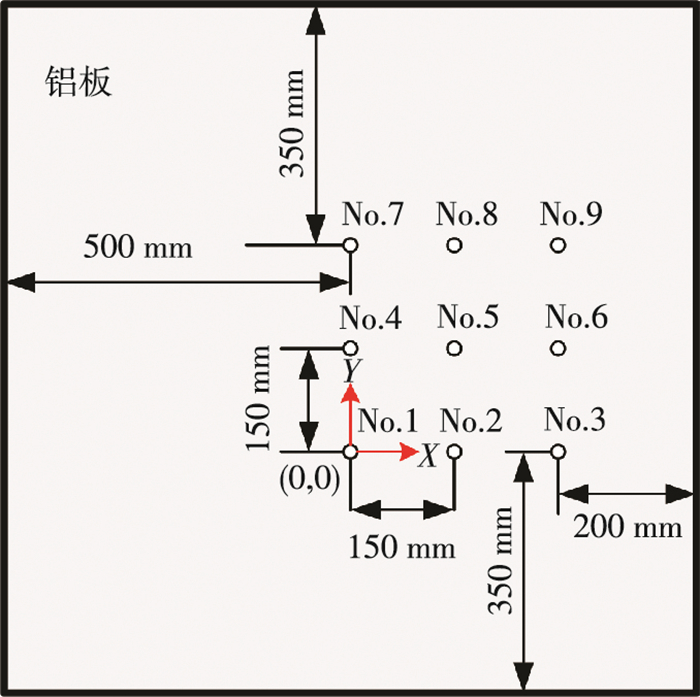
实验采用无锡海鹰企业集团有限责任公司的P51型压电传感器,压电传感器直径为10 mm,厚度为2 mm,实验件为1 000 mm×1 000 mm×5 mm的金属铝板.在铝板上粘贴第1个压电传感器,编号为1,粘贴位置定为坐标原点 (0, 0).在平板上共布置9个压电传感器 (编号1~9),组成3×3的正方形阵列.相邻两个压电传感器之间水平、垂直距离均为150 mm.传感器阵列距离右边边界200 mm,距离上方和下方边界均为350 mm,距离左边边界500 mm,如图 3所示.编号为1、2、3、4、5、6的压电传感器组成的长方形区域作为第1个基本检测单元,编号为4、5、6、7、8、9的压电传感器组成的长方形区域作为第2个基本检测单元.
|
图 3 压电传感器的布置 Figure 3 Arrangement of the piezoelectric sensors |
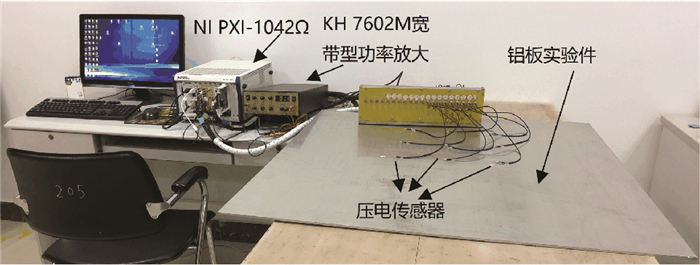
实验布置如图 4所示,激励信号采用中心频率为250 kHz的调制五波峰窄带波,激励信号由NI PXI 5441任意波形发生器产生,经过KH 7602M宽带型功率放大器放大,进而激励压电传感器产生Lamb波.NI TB 2605多路复合接线盒作为一个自动切换通道的开关,自动选择每个压电传感器作为激励.响应信号通过NI PXI 5105数据采集卡由其他压电传感器接收.NI PXI-1042Ω机箱集合了NI PXI 5441任意波形发生器、NI TB 2605多路复合接线盒和NI PXI 5105数据采集卡.采样频率设置为10 MHz.中心频率为250 kHz时的Lamb波的A0波群速度3 083 m/s,S0波的群速度为4 745 m/s.
|
图 4 实验布置 Figure 4 Experimental arrangement |
信号采集流程如下:对1号压电传感器进行激励,2~6号压电传感器接收信号;激励2号压电传感器,3~6号压电传感器接收信号;信号的激励、采集只在一个单元内进行.共采集2个单元内的信号.
按照先前提出的有效信号段自提取算法对信号进行处理,将提取出的有效信号段应用于损伤成像算法.损伤成像算法中的控制激励-接收路径影响范围的尺度因子参数β取1.02;图像增强因子α取10.放大倍数q取1.2,采用吸波胶模拟结构损伤.
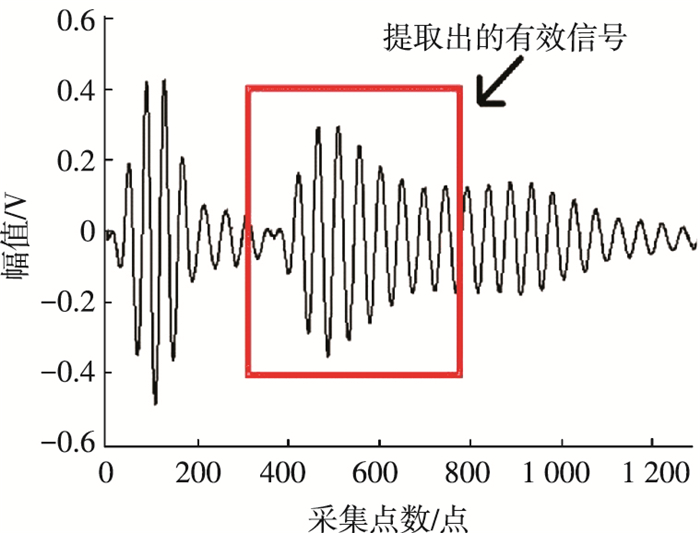
图 5给出了路径1-4采集到的原始信号和提取出的有效信号.1号传感器激励时,4号传感器接收到S0波和A0波所需的时间分别为31.6、48.6 μs,时间转换为相应的采集点数分别为316、486个点.此时,刚采集到A0波为第486个点,补偿的点数为250.0×1.2,等于300个点,即信号段的末尾为第786个点.因此提取出的路径1-4有效信号段的起始点为第316个点,结束点为第786个点.如图 5所示,图 5中方框所围的信号部分就是提取出的有效信号.根据同样的方法提取出的路径1-5有效信号段的起始点为第447个点,结束点为第988个点.提取出的路径1-6有效信号段的起始点为第707个点,结束点为第1 388个点.
|
图 5 路径1-4采集到的原始信号和提取出的有效信号 Figure 5 The original signal of path 1-4 collected and the effective signal extracted |
以4-9号传感器组成的基本检测单元为例分析对比实验中信号段长度的确定方法.
4号传感器激励时,7号传感器接收到S0波和A0波所需的时间分别为31.6、48.6μs,时间转换为相应的采集点数分别为316、486个点.以4号与7号传感器之间的距离来确定第1段参与计算的信号段长度.此时,刚采集到A0波为第486个点,补偿的点数为250.0×1.2,等于300个点,即信号段的末尾为第786个点,实际参与计算取第800个点.因此,该段信号段确定如下:第301个点为起始点,第800个点为结束点,信号段长度为500个点.
4号传感器激励时,8号传感器接收到S0波和A0波的相应点数为第447个点、第688个点.考虑到4号传感器与7号传感器之间的距离,不能遗漏掉该段距离有效的信号段,因此该段信号段确定如下:第301个点为起始点,第1 000个点为结束点,信号段长度为700个点.
4号传感器激励时,9号传感器接收到S0波和A0波的相应点数为第707个点、第1 088个点.该段信号段确定如下:第301个点为起始点,第1 400个点为结束点,信号段长度为1 100个点.
同时,为了考察无关信号的长度对损伤成像的影响,选取了第301个点为起始点,信号段长度分别为1 400、2 200、2 700个点的信号段参与损伤成像.
在铝板上粘贴两个模拟损伤.损伤点位置如图 6所示.一处模拟损伤位于主要路径1-6、2-4的直接路径上,次要路径1-5的间接路径上;另一处模拟损伤位于主要路径4-9、6-8的直接路径上.

|
图 6 双损伤位置 Figure 6 Double damage location |
现采用等长度信号段计算信号相关系数的方法来识别损伤.
将长度分别为500个点 (第301个点为起始点,第800个点为结束点)、700个点 (第301个点为起始点,第1 000个点为结束点)、1 100个点 (第301个点为起始点,第1 400个点为结束点) 的信号段参与双损伤成像比较.
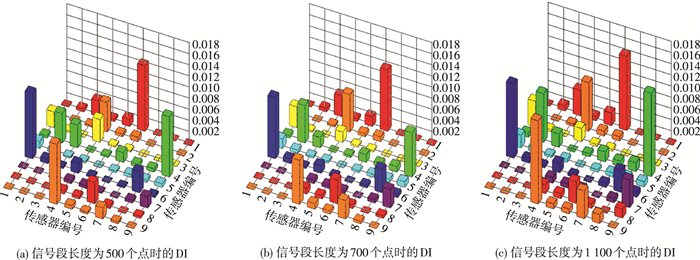
如图 7(a)所示,当信号段长度为500个点时,主要路径1-6、4-9的DI较大,主要路径2-4,6-8的DI次之,无损伤的路径3-4的DI大致等于主要路径2-4的DI.如图 7(b)所示,当信号段长度为700个点时,主要路径2-4、6-8的DI略微增长,主要路径1-6的DI减小,路径3-4、主要路径4-9的DI减小明显.如图 7(c)所示,当信号段长度增加到1 100个点时,随着路径4-9的有效信号段长度增加,DI增大明显,路径1-6、2-4都有不同程度的增大.
|
图 7 信号段长度分别为500、700、1 100个点时的DI Figure 7 DI of signal length being 500, 700 and 1 100 points respectively |
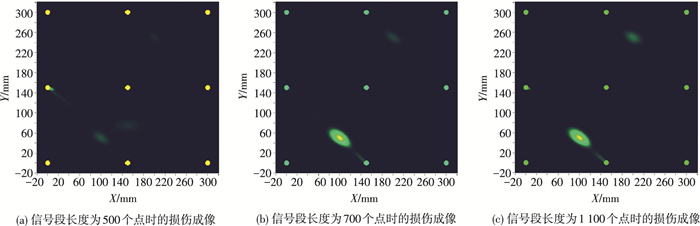
如图 8(a)所示,因为无损伤的路径3-4的DI大致等于主要路径2-4的DI,所以最终成像结果中出现路径1-6与路径3-4的虚假损伤,并且成像结果较暗淡,不清晰.当信号段包含的有效信号长度增加时,损伤所在的主要路径的DI总体都有所增加,损伤位置识别的比先前更明显,消除了虚假损伤,但还是有一个损伤不太明显.
|
图 8 信号段长度分别为500、700、1 100个点时的损伤成像 Figure 8 Damage imaging result of signal length being 500, 700 and 1 100 points respectively |
因此,有效信号段的长度太小时可能会导致成像图中出现实际不存在的损伤,且有的损伤不明显,不易观察到.随着有效信号段长度的增加,成像效果会随之改善,但仍有可能出现损伤成像不明显的现象.这是因为信号段长度的增加,会不同程度地影响各个DI,进而影响成像结果.
将长度分别为1 400个点 (第301个点为起始点,第1 700个点为结束点)、2 200个点 (第301个点为起始点,第2 500个点为结束点)、2 700个点 (第301个点为起始点,第3 000个点为结束点) 的信号段参与双损伤成像比较.
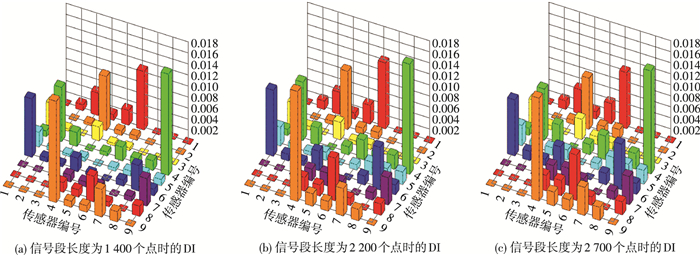
如图 9所示,随着信号段长度逐渐增加,信号段中无关信号段长度也随之增加,主要路径上1-6和路径4-9的DI都有所增加.
|
图 9 信号段长度分别为1 400、2 200、2 700个点时的DI Figure 9 DI of signal length being 1 400, 2 200 and 2 700 points respectively |
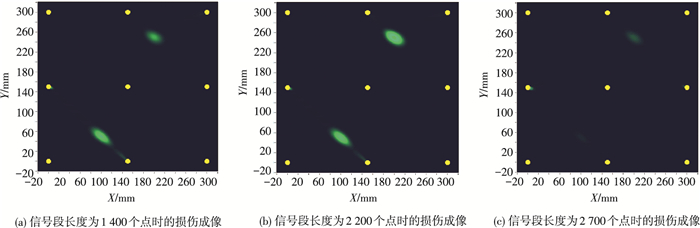
如图 10所示,损伤明亮程度随着信号段长度的增加先增强,后减弱,成像结果先由坏转好,再由好转坏,这是因为无关信号段的长度增加影响了DI,最终影响了成像效果.
|
图 10 信号段长度分别为1 400、2 200、2 700个点时的损伤成像 Figure 10 Damage imaging result of signal length being 1 400, 2 200 and 2 700 points respectively |
因此,适当的增加无关信号段的长度会改善成像效果,但若是增加太多的无关信号,会导致成像中的个别损伤暗淡,效果不明显.
4.2.2 自提取有效信号段应用于双损伤识别现采用有效信号段自提取算法计算信号相关系数的方法来识别损伤.
利用有效信号段自提取算法提取出的路径1-4有效信号段的起始点为第316个点,结束点为第786个点.提取出的路径1-5有效信号段的起始点为第447个点,结束点为第988个点.提取出的路径1-6有效信号段的起始点为第707个点,结束点为第1 388个点.在不同激励-接收路径采用不同长度的有效信号段计算信号相关系数,并得到损伤指标.
观察图 11,主要路径1-6、4-9的DI最大,主要路径2-4、6-8的DI次之,次要路径1-3的DI与主要路径6-8的DI差不多,无关路径的DI普遍较小,充分利用了有效信号段增大DI的优势,剔除了无关信号段对DI的不利影响.
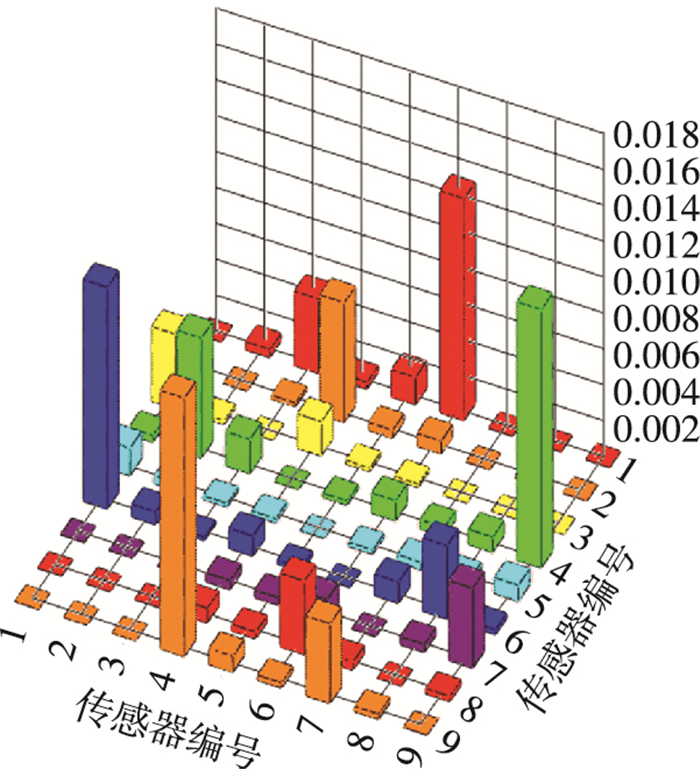
|
图 11 双损伤时的损伤指标柱状 Figure 11 The damage index histogram of double damage |
如图 12所示,应用自提取有效信号段参与损伤识别的成像图对损伤的识别效果较好,不需要人工选择信号段的长度,既可避免出现虚假损伤,又能避免出现另一损伤隐约可见的不理想效果,可以不受干扰、自动地识别出损伤,并清晰地显示出来.
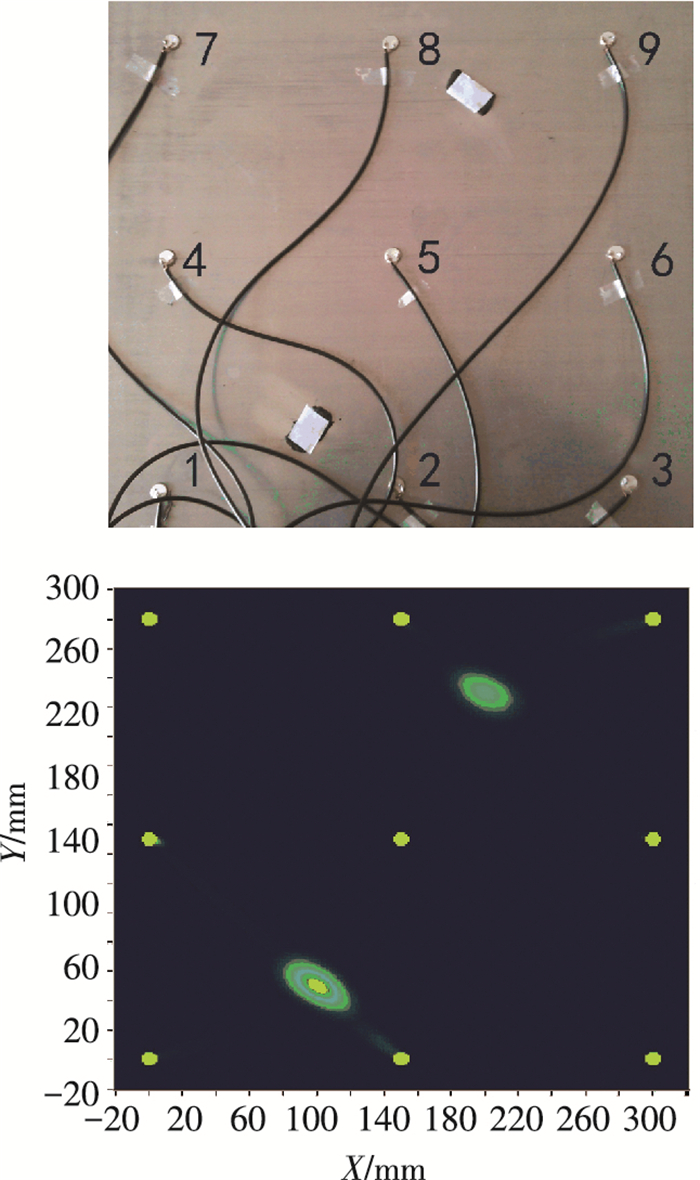
|
图 12 双损伤成像图与实际损伤图对比 Figure 12 Double damage imaging map contrast with the actual damage |
1) 提出了一种有效信号段自提取的算法,并结合区域分割方法,改进了成像算法,增强了成像效果,使得不会出现虚假损伤和遗漏真实损伤的现象,不再需要人为地选择参与计算的信号段长度,避免了人工操作对损伤识别结果带来的不利影响.
2) 能依据基本检测单元内的6个传感器组成的检测网络准确识别出每个单元内的单个损伤,并利用损伤成像算法将分布在不同基本检测单元内的多个损伤位置成像出来,直观明了地显示出多个损伤的位置.
| [1] |
冯勇明, 周丽, 李真. 基于匹配追踪的蜂窝夹层复合材料损伤检测[J].
仪器仪表学报, 2012, 33(4): 836-843.
FENG Yongming, ZHOU Li, LI Zhen. Research on honeycomb sandwich composite structure damage detection based on matching pursuit method[J]. Chinese Journal of Scientific Instrument, 2012, 33(4): 836-843. DOI: 10.3969/j.issn.0254-3087.2012.04.018 |
| [2] | ZHOU L, YUAN F G, MENG W J. A pre-stack migration method for damage identification in composite structures[J]. Smart Structures and Systems, 2007, 3(4): 439-454. DOI: 10.12989/sss.2007.3.4.439 |
| [3] | MIAO Xiaoting, WANG Dong, YE Lin, et al. Identification of dual notches based on time-reversal Lamb waves and a damage diagnostic imaging algorithm[J]. Journal of intelligent material system and structures, 2011, 22(17): 1983-1992. DOI: 10.1177/1045389X11421821 |
| [4] | MALINOWSKI P, WANDOWSKI T, TRENDAFILOVA I, et al. A phased array-based method for damage detection and localization in thin plates[J]. Structural Health Monitoring, 2008, 8(1): 5-11. DOI: 10.1177/1475921708090569 |
| [5] | JEONG H, JANG Y S. Wavelet analysis of plate wave propagation in composite laminates[J]. Composite Structures, 2000, 49(4): 443-450. DOI: 10.1016/S0263-8223(00)00079-9 |
| [6] | JEONG H, JANG Y S. Fracture source location in thin plates using the wavelet transform of dispersive waves[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2000, 47(3): 612-619. DOI: 10.1109/58.842048 |
| [7] | HUANG N E, SHEN Zheng, LONGS R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A, 1998, 454(1971): 903-995. DOI: 10.1098/rspa.1998.0193 |
| [8] | HUANG N E, SHEN Zheng, LONG S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457. DOI: 10.1146/annurev.fluid.31.1.417 |
| [9] | HAY T R, ROYER R L, GAO Huidong, et al. A comparison of embedded sensor Lamb wave ultrasonic tomography approaches for material loss detection[J]. Smart Material and Structures, 2006, 15(4): 946-951. DOI: 10.1088/0964-1726/15/4/007 |
| [10] | WANG Dong, YE Lin, LU Ye. A probabilistic diagnostic algorithm for identification of multiple notches using digital damage fingerprints (DDFs)[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(12): 1439-1450. DOI: 10.1177/1045389X09338323 |
| [11] | ROSALIE S C, VAUGHAN M, BREMNER A, et al. Variation in the group velocity of Lamb waves as a tool for the detection of delamination in GLARE aluminium plate-like structures[J]. Composite Structures, 2004, 66(1/2/3/4): 77-86. DOI: 10.1016/j.compstruct.2004.04.024 |
| [12] | GRONDEL S, ASSAAD J, DELEBARRE C, et al. Health monitoring of a composite wingbox structure[J]. Ultrasonics, 2004, 42(1/2/3/4/5/6/7/8/9): 819-824. DOI: 10.1016/j.ultras.2004.01.058 |
| [13] | BIEMANS C, STASZEWSKI W J, BOLLER C, et al. Crack detection in metallic structures using broadband excitation of acousto-ultrasonics[J]. Journal of Intelligent Material Systems and Structures, 2001, 12(8): 589-597. DOI: 10.1177/10453890122145366 |
| [14] | IHN J B, CHANG F K. Detection and monitoring of hidden fatigue crack growth using a built-in piezoelectric sensor/actuator network: Ⅰ. diagnostics[J]. Smart Materials and Structures, 2004, 13(3): 621-630. DOI: 10.1088/0964-1726/13/3/021 |
| [15] |
何志全, 周丽, 孙虎. 基于传递阻抗能量的无基准Lamb波裂纹检测[J].
工程力学, 2014, 31(7): 250-256.
HE Zhiquan, ZHOU Li, SUN Hu. Reference-free Lamb wave crack detection based on transfer impedance energy[J]. Engineering Mechanics, 2014, 31(7): 250-256. DOI: 10.6052/j.issn.1000-4750.2013.01.0113 |
| [16] |
郑阳, 周进节. 兰姆波在裂纹处的模态转换及散射特性研究[J].
工程力学, 2014, 31(6): 21-29.
ZHENG Yang, ZHOU Jinjie. Mode conversion and scattering properties of Lamb waves near localized cracking[J]. Engineering Mechanics, 2014, 31(6): 21-29. DOI: 10.6052/j.issn.1000-4750.2012.12.0982 |
 2017, Vol. 49
2017, Vol. 49


