2. 哈尔滨工业大学 (威海) 信息与电气工程学院,山东 威海 264209;
3. 东华理工大学 江西省质谱科学与仪器重点实验室,南昌 330013
2. School of Information and Electrical Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, Shandong, China;
3. Jiangxi Key Laboratory for Mass Spectrometry and Instrumentation, East China University of Technology, Nanchang 330013, China
质谱仪中质量分析器所需的高真空条件阻碍了质谱仪的小型化与便携化.如果在保证必要性能的同时,在低真空条件下进行质量分析,可以极大地简化真空系统和离子传输系统、减小质谱仪的体积、降低功耗和成本,使其可以更广泛地应用于现场实时检测.低真空下的质量分析将引领小型质谱仪的下一次革新[1].
四极杆质量分析器是目前最成熟、应用最广泛的质量分析器之一,它由四根平行的金属杆组成,通过在四根金属杆上施加交变电压,可以在其内部形成马鞍形的四极场,实现不同质荷比离子的选择.离子在四极场中的运动分为稳定和不稳定两种情况[2],稳定区决定了质谱仪工作的质量扫描线,因此,稳定区的确定是进行质量分析的前提.
针对低真空度下稳定区和质量分析机理,Whetten[3]指出有阻力时粒子的运动仍可以用Mathieu方程进行描述,并给出了粒子的运动模型,但没有讨论稳定区的变化;Hasegawa等[4]利用数学分析方法分析了有阻力情况下稳定区的变化,但仅讨论了第一和第二稳定区;Whitten等[5]讨论了第一稳定区的变化,讨论更侧重于数学上对离子运动频率的分析.此外,Vinitsky等[6]观察了四极场中离子的异形运动,利用非线性力和非线性场对此进行了解释;Xu等[7-8]利用碰撞模型和实验,讨论了阻力对离子的捕获、出射以及分辨率的影响.
作为低真空下进行质量分析的理论基础,稳定区随真空度变化的研究和一套精度高且适用于实际工程需求的稳定区确定方法是不可或缺的,而现有研究均没有相关的讨论.基于此,本文针对四极杆质量分析器,利用高精度数值方法计算不同阻尼条件下的离子运动轨迹,进而得到不同阻尼条件下第一、第二以及高阶稳定区.同时,讨论阻尼系数的影响因素,分析相应的质量分析机理.
1 模型与计算 1.1 有阻尼条件下的离子运动在四极杆质量分析器中,如果两个相对电极的距离为2r0,在两对电极上分别施加电势+ φ0和-φ0,则可以在质量分析器中形成四极场,其中φ0= U-Vcos Ωt,U为所加电势的直流分量,V为交流分量的幅度,Ω为交流分量的角频率,t为时间.根据拉普拉斯方程及边界条件,四极场中 (x, y) 点的电势为
| $ \varphi \left( {x,y} \right) = \frac{{{\varphi _0}}}{{r_0^2}}\left( {{x^2} - {y^2}} \right) = \frac{{\left( {{x^2} - {y^2}} \right)\left( {U - V\cos \mathit{\Omega t}} \right)}}{{r_0^2}}. $ |
以u代表x或y方向,如果离子在u方向的运动速度为vu,根据斯托克斯定律,离子在u方向所受到的阻力为fu=-Dvu,其中D为粘滞系数.在u方向,由力的平衡有
| $ m\frac{{{{\rm{d}}^2}u}}{{{\rm{d}}{t^2}}} + D\frac{{{\rm{d}}u}}{{{\rm{d}}t}} + \frac{{2e\left( {U - V\cos \mathit{\Omega t}} \right)}}{{r_0^2}}u = 0, $ |
令ξ=Ωt/2,有
| $ \frac{{{{\rm{d}}^2}u}}{{{\rm{d}}{\xi ^2}}} + k\frac{{{\rm{d}}u}}{{{\rm{d}}\xi }} + \left( {{a_u} - 2{q_u}\cos 2\xi } \right)u = 0, $ | (1) |
式中:
| $ \begin{array}{l} {a_u} = {a_x} = - {a_y} = \frac{{8eU}}{{mr_0^2{\mathit{\Omega }^2}}},{q_u} = {q_x} = - {q_y} = \frac{{4eV}}{{mr_0^2{\mathit{\Omega }^2}}},k = \\ \frac{D}{m} \cdot \frac{1}{\mathit{\Omega }}. \end{array} $ | (2) |
式 (1) 描述了低真空环境中有阻尼的离子运动,为带有阻尼项的Mathieu方程,与标准Mathieu方程相比增加了kdu/dξ的阻尼项,称k为阻尼系数,与压强有关,当k=0时,即转化为标准Mathieu方程.
1.2 带阻尼项Mathieu方程的数值解法带阻尼项Mathieu方程为二阶微分方程,利用数学分析的方法求解它的稳定区是十分复杂的.若将其转化为差分方程,利用计算机就可以快速计算其稳定区,更适用于工程需要.龙格-库塔方法是一种高精度单步数值方法,在离子轨迹仿真中,四阶算法是最常用的算法,但由于阻力的存在,离子轨迹变得复杂,且高阶稳定区的范围很小,因此,需要更高精度的算法来确定有阻力条件下的稳定区.研究表明,五阶龙格-库塔法精度高于四阶的约11倍[9],且稳定性和收敛性明显优于四阶算法.
令v=du/dξ,可将方程 (1) 转化为一阶微分方程组,应用Butcher RK5形式[9],得
| $ \left\{ \begin{array}{l} u\left( {n + 1} \right) = u\left( n \right) + \frac{h}{{90}}\left( {7{M_1} + 32{M_3} + 12{M_4} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {32{M_5} + 7{M_6}} \right),\\ v\left( {n + 1} \right) = v\left( n \right) + \frac{h}{{90}}\left( {7{N_1} + 32{N_3} + 12{N_4} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {32{N_5} + 7{N_6}} \right), \end{array} \right. $ | (3) |
其中,u表示离子运动的位移,v表示离子运动对频率归一化后的速度,h为计算步长.参数Mn与Nn的数学表达式为
| $ {M_1} = v\left( n \right), $ |
| $ {N_1} = - \left\{ {a + 2q\cos 2\left[ {\left( {n - 1} \right)h} \right]} \right\}u\left( n \right) + kv\left( n \right), $ |
| $ {M_2} = v\left( n \right) + \frac{h}{4}{N_1}, $ |
| $ \begin{array}{l} {N_2} = - \left\{ {a + 2q\cos 2\left[ {\left( {n - 1} \right)h + \frac{h}{4}} \right]} \right\}\left[ {u\left( n \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{h}{4}{M_1}} \right] + k\left[ {v\left( n \right) + \frac{h}{4}{N_1}} \right], \end{array} $ |
| $ {M_3} = v\left( n \right) + \frac{h}{8}\left( {{N_1} + {N_2}} \right), $ |
| $ \begin{array}{l} {N_3} = - \left\{ {a + 2q\cos 2\left[ {\left( {n - 1} \right)h + \frac{h}{4}} \right]} \right\}\left[ {u\left( n \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{h}{8}\left( {{M_1} + {M_2}} \right)} \right] + k\left[ {v\left( n \right) + \frac{h}{8}\left( {{N_1} + {N_2}} \right)} \right], \end{array} $ |
| $ {M_4} = v\left( n \right) - \frac{h}{2}{N_2} + h{N_3}, $ |
| $ \begin{array}{l} {N_4} = - \left\{ {a + 2q\cos 2\left[ {\left( {n - 1} \right)h + \frac{h}{2}} \right]} \right\}\left[ {u\left( n \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {h{M_3} - \frac{h}{2}{M_2}} \right] + k\left[ {v\left( n \right) - \frac{h}{2}{N_2} + h{N_3}} \right], \end{array} $ |
| $ {M_5} = v\left( n \right) + \frac{h}{{16}}\left( {3{N_1} + 9{N_4}} \right), $ |
| $ \begin{array}{l} {N_5} = - \left\{ {a + 2q\cos 2\left[ {\left( {n - 1} \right)h + \frac{3h}{4}} \right]} \right\}\left[ {u\left( n \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{h}{{16}}\left( {3{M_1} + 9{M_4}} \right)} \right] + k\left[ {v\left( n \right) + \frac{h}{{16}}\left( {3{N_1} + 9{N_4}} \right)} \right], \end{array} $ |
| $ {M_6} = v\left( n \right) + \frac{h}{7}\left( { - 3{N_1} + 2{N_2} + 12{N_3} - 12{N_4} + 8{N_5}} \right), $ |
| $ \begin{array}{l} {N_6} = - \left\{ {a + 2q\cos 2\left[ {\left( {n - 1} \right)h + h} \right]} \right\}\left[ {u\left( n \right) + \frac{h}{7}\left( - \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {3{M_1} + 2{M_2} + 12{M_3} - 12{M_4} + 8{M_5}} \right)} \right] + k\left[ {v\left( n \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {\frac{h}{7}\left( { - 3{N_1} + 2{N_2} + 12{N_3} - 12{N_4} + 8{N_5}} \right)} \right]. \end{array} $ |
在表达式中,a和q可直接进行赋值,如第一稳定区与q轴的交点a=0,q=0.908,也可以根据式 (2) 通过指定扫描电压U和V、扫描频率Ω和质荷比m/e,计算后得到相应的a和q.其中,扫描频率一般以Hz进行表述.
在MATLAB中,对于不同的a和q,给定计算步长h,离子初始位置u(0),离子初速度v(0),根据式 (3) 经过n次迭代计算,即可得到不同a和q值下离子运动轨迹矩阵u和归一化速度矩阵v.此外,可以通过对u进行快速傅里叶变换得到轨迹的频谱特性;根据du/dt=(Ω/2) du/dξ可得到离子的运动速度特性.
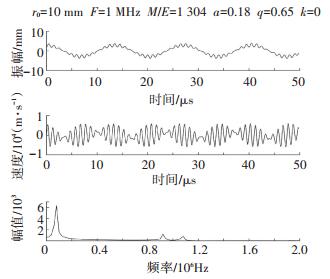
2 结果与讨论 2.1 真空条件下离子运动的仿真仿真条件如下:电极距离r0= 10 mm,离子初始位置ux=uy=0.2r0,初速度vx=vy=0,步长h=0.01π,扫描电压U= 1.23 kV、V= 8.77 kV,扫描频率Ω=1 MHz,阻尼系数k=0.在此条件下,对于质荷比为1 304的离子a=0.18,q=0.64,由四极杆基本理论可知该点位于稳定区内部,运动是稳定的. 图 1给出了离子在y方向的运动轨迹、速度以及频谱特性,图 2给出了离子在x-y平面的运动轨迹.
|
图 1 a=0.18, q=0.64, k=0时y方向离子运动特性 Figure 1 Characteristics of ion motion when a= 0.18, q=0.64, k=0 |
|
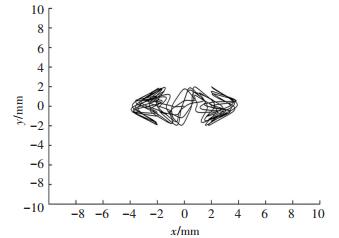
图 2 a=0.18, q=0.64, k=0时x-y平面离子运动轨迹 Figure 2 Trajectory of ion motion when a= 0.18, q=0.64, k=0 |
由图 1可知,离子运动为带有扰动的正弦周期振荡,由能量守恒可知,离子的最大振幅为初始位置.由频谱特性可知,离子的运动是基频和高次频率振荡运动的叠加,基频近似为80 kHz,高次频率分别为0.92和1.08 MHz,离子振荡运动基频占主要成分.离子运动稳定,与理论相符.
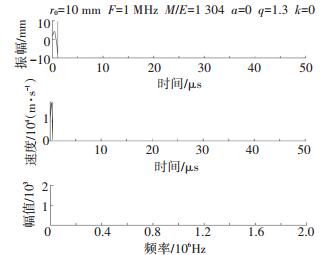
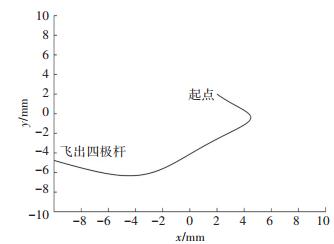
其他条件不变,改变扫描电压U和V,使a=0,q=1.3,由于q值大于真空条件下稳定区的边界 (0, 0.908),运动是不稳定的. 图 3、图 4给出了该条件下离子的运动特性仿真结果,离子在四极场中从起点 (x, y)=(2, 2) 开始运动,很快从x=-10 mm的边界飞出四极杆,不能被检测.
|
图 3 a=0, q=1.3, k=0时y方向离子运动特性 Figure 3 Characteristics of ion motion when a=0, q=1.3, k=0 |
|
图 4 a=0, q=1.3, k=0时x-y平面离子运动轨迹 Figure 4 Trajectory of ion motion when a=0, q=1.3, k=0 |
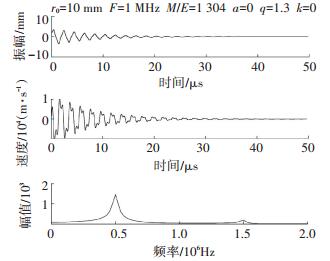
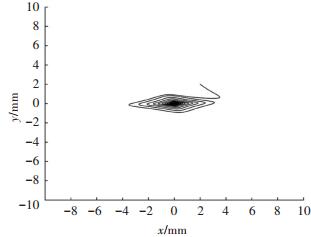
针对图 3所示的仿真条件,其他条件不变,改变阻尼系数,当k=1时离子的运动特性如图 5、图 6所示.离子以 (x, y)= (2, 2) 为起点开始运动,由于真空度降低,离子与气体分子发生碰撞降低了离子的轴向动能和径向发散度,最终趋于四极杆中心,运动是稳定的,且运动具有一定的周期性.对比图 3和图 5,阻尼项的存在使离子的运动由不稳定变为稳定.
|
图 5 a=0, q=1.3, k=1时y方向离子运动特性 Figure 5 Characteristics of ion motion when a=0, q=1.3, k=1 |
|
图 6 a=0, q=1.3, k=1时x-y平面离子运动轨迹 Figure 6 Trajectory of ion motion when a=0, q=1.3, k=1 |
相同条件下,阻尼系数k的变化使离子的运动特性发生了变化.因此,k值必然影响稳定区,进而影响离子的操作模式.
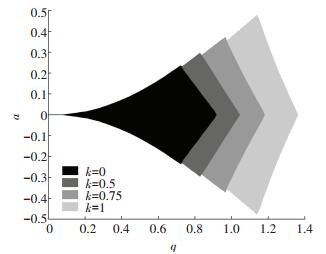
2.3 不同阻尼系数下的稳定区基本仿真条件不变,即电极距离r0= 10 mm,离子初始位置ux=uy=0.2r0,初速度vx=vy=0,步长h=0.01π.针对不同的k值,仿真不同 (a, q) 下的离子运动轨迹,对于离子飞行5 ms后振幅仍小于r0的 (a, q) 点标记稳定,这样通过扫描a和q即可得到不同k值下的稳定区. 图 7给出了当k在0到1变化时,第一稳定区的变化.
|
图 7 不同k值下的第一稳定区 Figure 7 The first stability regions under different damping coefficient |
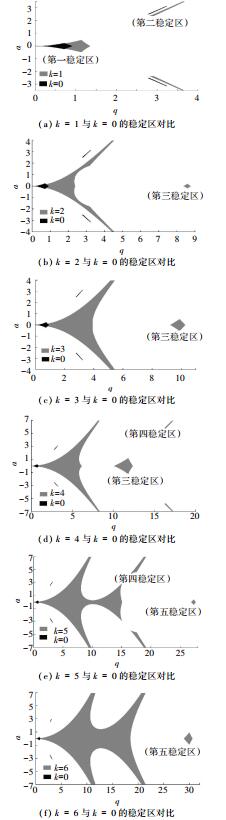
图 8给出了当k从1到6变化时,不同k值下的稳定区. 图 8(a)中,k值从0到1的变化使稳定区发生了移动和扩展,这在第二稳定区尤为明显;图 8(b)中,当k=2时,稳定区继续扩展,第一和第二稳定区连接到一起,第三稳定区开始出现;随着k值的增大,稳定区表现出持续变大并连接到一起、新的稳定区不断出现的趋势.
|
图 8 不同k值下稳定区的变化 Figure 8 The stability regions under different damping coefficient |
1) 随着k值的增加稳定区总体向右扩展,并多个稳定区不断连接到一起,即k值增加,更大的q值依旧可以使离子稳定运动. 图 3和图 5所示的a=0,q= 1.3就是这样的一个例子,当k=0时,该点的q值较大,离子在四极场中获得了很大的能量,是一个不稳定的发散运动,而当k值增大到1时,阻力的存在减小了离子运动的能量,进而使运动稳定,且振幅逐渐减小.
2) 在q值较小时,随着k值的增加,可以使离子稳定运动的a值范围减小,因此,当q值较小时,对于靠近稳定区边界的点,k值的增加可能使离子由稳定运动变为不稳定.
2.4 阻尼系数k的影响因素与离子操作模式在实际的四极杆实验中,当真空度降低,稳定区变化,对于同一种离子,利用原有的质量扫描线进行实验,必将导致分辨率的下降.因此,为得到更优的分辨率,必须改变扫描电压,根据当前真空度和扫描频率所决定的稳定区,选择新的扫描线进行实验.
由式 (2),k是一个与粘滞系数D、离子质量m和扫描频率Ω相关的物理量.粘滞系数D与离子的形状、背景气体的压强、碰撞粒子的相对速度、碰撞频率等因素有关,因此很难精确计算D,但一般可以认为D/m项与压强具有线性关系[5].文献[10]的实验结果表明,对于质荷比为84的84Kr,以氦气作为背景气体,当压强为0.057 Pa时,D/m在数值上约为500.因此,D/m项可以近似表述为
| $ \frac{D}{m}\left( p \right) \approx \frac{{500}}{{0.057}}p. $ |
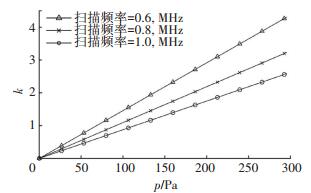
图 9给出了不同扫描频率下压强p与阻尼系数k的关系.在扫描频率不变的条件下,阻尼系数k随压强p线性增加.此外,相同压强下,k值与扫描频率Ω有关,在高真空度下,D趋于0,扫描频率Ω的变化几乎不会影响k.如果提高压强和扫描频率Ω,可以削弱D项对k值的影响,有利于质量分析.
|
图 9 不同扫描频率下p与k的关系 Figure 9 Relationship between p and k in different scanning frequency |
1) 针对低真空下的质量分析,根据有阻力条件下离子的运动,得到了修正的马修方程,提出了利用五阶龙格-库塔数值方法确定稳定区的方法.
2) 得到了不同阻尼系数k下,第一、第二以及高阶稳定区的变化趋势.随着阻尼系数k的增大,稳定区发生变化,不断变大,并连接在一起,稳定区的确定为确定质量扫描线和离子操作模式提供了理论基础.
3) 阻尼系数k对稳定区有很大的影响,从数学模型上看,提高扫描频率更有利于低真空度下的质量分析.
| [1] | SNYDER D T, PULLIAM C J, OUYANG Z, et al. Miniature and fieldable mass spectrometers: recent advances[J]. Analytical Che-mistry, 2015, 88(1): 2-29. DOI: 10.1021/acs.analchem.5b03070 |
| [2] | MARCH R E. An introduction to quadrupole ion trap mass spectro-metry[J]. Journal of Mass Spectrometry, 1997, 32(4): 351-369. DOI: 10.1002/(SICI)1096-9888(199704)32:4 |
| [3] | WHETTEN N R. Macroscopic particle motion in quadrupole fields[J]. Journal of Vacuum Science & Technology, 1974, 11(2): 515-518. |
| [4] | HASEGAWA T, UEHARA K. Dynamics of a single particle in a paul trap in the presence of the damping force[J]. Applied Physics B, 1995, 61(2): 159-163. DOI: 10.1007/BF01090937 |
| [5] | WHITTEN W B, REILLY P T A, RAMSEY J M. High-pressure ion trap mass spectrometry[J]. Rapid Communications in Mass Spectrometry, 2004, 18(15): 1749-1752. DOI: 10.1002/rcm.1549 |
| [6] | VINITSKY E A, BLACK E D, LIBBRECHT K G. Particle dynamics in damped nonlinear quadrupole ion traps[J]. American Journal of Physics, 2015, 83(4): 313-319. DOI: 10.1119/1.4902185 |
| [7] | XU W, SONG Q, SMITH S A, et al. Ion trap mass analysis at high pressure: a theoretical view[J]. Journal of the American Society for Mass Spectrometry, 2009, 20(11): 2144-2153. DOI: 10.1016/j.jasms.2009.06.019 |
| [8] | SONG Q, XU W, SMITH S A, et al. Ion trap mass analysis at high pressure: an experimental characterization[J]. Journal of Mass Spectrometry, 2010, 45(1): 26-34. DOI: 10.1002/jms.1684 |
| [9] |
贺木易, 邵睿婷, 冯焱, 等. 离子阱质谱中离子轨迹算法研究[J].
质谱学报, 2015, 36(3): 217-222.
HE Muyi, SHAO Ruiting, FENG Yan, et al. Study of the simulation method about ion trajectory[J]. Journal of Chinese Mass Spectrometry Society, 2015, 36(3): 217-222. DOI: 10.7538/zpxb.youxian.2014.0070 |
| [10] | PLASS W R, GILL L A, BUI H A, et al. Ion mobility measurement by DC tomography in an RF quadrupole ion trap[J]. The Journal of Physical Chemistry A, 2000, 104(21): 5059-5065. DOI: 10.1021/jp994356c |
 2017, Vol. 49
2017, Vol. 49


