2. 东北电力大学 信息工程学院,吉林 吉林 132012;
3. 长春理工大学 电子信息工程学院,长春 130022
2. School of Information Engineering, Northeast Dianli University, Jilin 132012, Jilin, China;
3. School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China
随着网络技术的发展,无数智能节点通过无线通信技术连接在一起,形成了无所不能的物联网[1].其中位置服务[1-2]是物联网面向用户的关键需求之一,而位置服务主要依赖于无线定位技术.无线定位技术从地理位置上可分为室内定位以及室外定位.室外定位一般通过卫星导航系统辅助以AGPS进行定位,具有定位精度适中、定位速度快等优点.然而卫星信号穿透能力弱,受到建筑物外墙的阻挡,无法为室内设备提供定位服务.室内无线信号环境相对于室外要复杂得多.相对于室外环境,室内环境有建筑物墙体、房间布局等带来的无线信号多径效应影响以及多种室内无线设备对定位信号带来的干扰等,这与室外定位具有很大的不同.
随着智能手机等内置无线接入的设备普及率的提高,Wi-Fi信号已经广泛分布在大多数室内环境,学者们提出了多种利用Wi-Fi信号进行室内定位的技术[3-4],包括到达角度 (AOA) 定位、到达时间 (TOA) 定位、到达时间差 (TDOA) 定位、信号强度 (RSSI) 定位、位置指纹定位[5]等.上述室内定位方法中,AOA定位需要硬件额外增加精确测量角度的硬件—天线,设备的广泛适用性受到了限制;TOA和TDOA定位方法需要精准测量信号在空间中传播的时间,这对设备硬件提出了很高的要求,成本受限的设备往往不适用;利用RSSI测距定位不需要额外的硬件,成本较低,但受到环境影响较大,在复杂的室内环境中定位精度较差.基于Wi-Fi技术的位置指纹定位利用多个无线接入点在室内不同位置的信号强度值差异,预先建立位置坐标与离线信号强度的指纹数据库,作为在线定位的依据.采用RSSI信息作为指纹数据库的在线定位技术,定位时不需要额外增加硬件,在综合应用场景下具有成本和广泛适用性的优势[6].
位置指纹定位方法包括离线建立位置指纹数据库和在线位置指纹数据匹配估算位置两个阶段.典型的位置指纹数据匹配算法包括最近邻法 (Nearest Neighbor, NN)[7]、K近邻法 (K-NN)[8]和加权K近邻法 (Weighted KNN, WKNN)[9-12]等.在以上典型位置指纹定位的方法中,学者们针对优化离线指纹数据库和改进在线定位匹配算法两方面同时展开研究:文献[13]利用核函数、文献[14]利用Kalman滤波等对离线数据进行分析及优化,从位置指纹数据来源上使定位所需匹配数据更加精确;文献[15]利用多高斯混合模型构建离线指纹数据库,并用期望最大值作为估计模型参数的算法,增加了系统定位的精度;文献[16]利用最小二乘法对位置指纹信息拟合成高斯多项式连续分布曲线,对于信号强度分布较为平滑的室内空间具有较高的定位精度.以上位置指纹定位算法的改进和优化,在对离线位置指纹数据库的分析优化和提高采样值精度方面作了相应的改进,提高了定位精度.
由于室内墙壁、门及其他物体的隔挡,室内各Wi-Fi信号RSSI衰落分布并不一定都很平滑,基于欧氏距离的加权K近邻算法会因此带来一定误差.本文从位置指纹数据与实际采样值的相关性入手,首先通过聚类算法对离线位置指纹数据进行分类,排除与实测采样值差别较大的数据,增大位置指纹数据与采样值的相关性,降低位置匹配算法的计算量;然后通过数据相关性对指纹数据进行分析,根据与实测采样值位置指纹数据的离散程度,对离散程度不同的位置指纹数据赋予不同的权值,利用加权K近邻法估计待定位位置.
1 基于K-means算法的离线位置指纹库建立及聚类位置指纹定位方法首先要做的是建立基于位置和信号参数的离线位置指纹数据库.本文所采用的离线指纹数据是定位区域内已知位置上设备能够获得的环境中各个无线接入点的信号强度采样值,即RSSI.然而指纹数据若选取不当,会增大在线匹配位置时的误差.利用K-means聚类算法将离线指纹数据进行聚类,实测采样值只与聚类后的聚类中心欧氏距离最短的一些离线指纹数据进行RSSI值近似匹配,可减小估计误差.假设各个无线接入点无线信号发射功率不变但位置未知,假设定位空间为二维平面.
1.1 初始位置指纹数据库的建立设某一定位区域离线位置指纹数据库的建立需要D个采样点数据,每个采样点的二维空间位置可以表示为 (xi, yi),i=1, …, D.在每个采样点能够获得N个无线接入点的信号强度值,可以用向量形式表示,如式 (1) 所示:
| ${F_{{\rm{RSS}}{{\rm{N}}_i}}} = \left( {{f_{i1}},{f_{i2}}, \cdots ,{f_{iN}}} \right),i = 1, \cdots ,D.$ | (1) |
该组信号强度值的组合对应的二维空间坐标如式 (2) 所示:
| ${S_i} = \left( {{x_i},{y_i}} \right),i = 1, \cdots ,D.$ | (2) |
因此每组指纹信息的数据结构可以表示为如式 (3) 所示的形式:
| $\begin{array}{l} {G_{{\rm{RSS}}{{\rm{N}}_i}}} = \left( {{S_i},{F_{{\rm{RSS}}{{\rm{N}}_i}}}} \right) = \left( {{x_i},{y_i},{f_{i1}},{f_{i2}}, \cdots ,{f_{iN}}} \right),\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad i = 1,2, \cdots ,D. \end{array}$ | (3) |
将采集到的位置指纹数据以行形式存储,得到全部离线位置指纹的数据库,如式 (4) 所示:
| $G = \left[ {\begin{array}{*{20}{l}} {{x_1}} & {{y_1}} & {{f_{11}}} & {{f_{12}}} & \cdots & {{f_{1N}}}\\ {{x_2}} & {{y_2}} & {{f_{21}}} & {{f_{22}}} & \cdots & {{f_{2N}}}\\ {\; \vdots } & {\; \vdots } & {\; \vdots } & {\; \vdots } & \ddots & {\; \vdots }\\ {{x_D}} & {{y_D}} & {{f_{D1}}} & {{f_{D1}}} & \cdots & {{f_{DN}}} \end{array}} \right].$ | (4) |
这是位置指纹数据库的初始状态.
1.2 基于K-means算法的离线位置指纹数据聚类为了降低从位置指纹数据库中查找匹配指纹的计算量,采用基于K-means的聚类算法进行聚类,得到聚类后的位置指纹数据库.具体的聚类过程如下.
1) 在1.1节中离线位置指纹数据库中的D个指纹信息FRSSNi作为待聚类的原始指纹信息,其维度为检测到无线接入点RSSI值的个数N.同时指定需要聚类的数目K(K≤D);从D个指纹信息中任意选取K个指纹为初始的聚类中心集合C,如式 (5) 所示:
| $C = \left( {{F_{{\rm{RSSN1}}}},{F_{{\rm{RSSN2}}}}, \cdots ,{F_{{\rm{RSSN}}k}}} \right).$ | (5) |
2) 计算剩余的D-K个指纹与C中各个聚类中心的欧氏距离Eij(i=1, 2, …, D-K, j=1, 2, …, K),找到距离该指纹最近的聚类中心Ci,将该指纹归类到该聚类中,得到总共含有D个指纹信息的K个聚类C1, C2, …, CK,每个聚类中的指纹信息个数定义为nck.
3) 依据式 (6) 重新计算K个聚类各自的聚类中心,替代原有的聚类中心:
| ${{F'}_{{\rm{RSS}}{{\rm{N}}_i}}} = \frac{1}{{{n_{ci}}}}\sum\limits_1^{{n_{ci}}} {{F_{{\rm{RSS}}{{\rm{N}}_i}}}} ,\left( {{F_{{\rm{RSS}}{{\rm{N}}_i}}} \subset {C_i},i = 1,2, \cdots ,K} \right).$ | (6) |
4) 重复步骤2)-3),直至重新计算出的聚类中心值与上一步的聚类中心相等,即聚类收敛到极值,至此聚类结束,得到最终的离线位置指纹信息聚类.
2 离散程度相关的位置指纹定位算法及定位流程 2.1 算法描述WKNN算法相对于K近邻算法能够有效利用k个离线位置指纹的权重,实现更精确的位置估算,对k个位置指纹数据权重系数值的选取决定了定位误差的大小.本文提出一种基于参考位置指纹离散程度的WKNN定位算法 (Discrete Degree WKNN, DD-WKNN).在离线位置指纹数据中选取与在线实测RSSI值欧氏距离最短的K个离线位置指纹数据,依据离线位置指纹离散程度对位置估算的参考权重进行权值设定,离散程度用这k个位置指纹的变异系数表示,然后借鉴WKNN算法进行归一化加权求和,权重系数的大小与实测采样值所参考的K个位置指纹的离散程度成反比.对于参考的离散程度较小的位置指纹数据,说明其位置附近RSSI值分布较为平滑,估测待测定位置时给予较大参考权值,离散程度较大的位置说明RSSI在该位置附近有较大的变化,参考价值较低,估测待测定位置时给予较低的参考权值.因此,此方法应用在室内环境复杂、Wi-Fi信号强度衰落不均衡的环境中,可以增加定位的精确度,降低定位误差波动.具体算法如下.
1) 待定位位置RSSI实测采样值记为FRSSNLoc,选取k个与FRSSNLoc欧氏距离最小的k个离线位置指纹集合,记为LFk,可表示为如式 (7) 的形式.
| ${G_k} = {\left[ {{F_{RSSI}}} \right]_k} = {\left[ {\begin{array}{*{20}{l}} {{f_{11}}} & {{f_{12}}} & \cdots & {{f_{1N}}}\\ {{f_{21}}} & {{f_{22}}} & \cdots & {{f_{2N}}}\\ {\;\; \vdots } & {\;\; \vdots } & {\;\; \vdots } & {\;\; \vdots }\\ {{f_{k1}}} & {{f_{k2}}} & \cdots & {{f_{kN}}} \end{array}} \right]_{k \times N}}.$ | (7) |
2) 对LFk中的k个位置指纹,统计每个位置指纹FRSSNi(i=1, …, k) 中的各个RSSI值均值
| $\begin{array}{l} \quad \quad \overline {{f_i}} = \frac{1}{N}\sum\limits_{j = 1}^N {{f_{ij}}} ,\\ {s_i} = \sqrt {\frac{1}{{N - 1}}\sum\limits_{j = 1}^N {{{\left( {{f_{ij}} - {{\overline f }_i}} \right)}^2}} } ,\\ \quad \quad \left( {i = 1, \cdots ,k} \right) \end{array}$ | (8) |
| ${v_i} = \frac{{{s_i}}}{{\overline {{f_i}} }}.$ | (9) |
3) 为了将参考位置指纹的离散程度与位置估计结合,将vi归一化,设权重系数为wi,令wi=
4) 根据得到的权重系数,对各个参考位置进行加权求和,估算位置坐标.具体如式 (10) 所示:
| $\hat x = \sum\limits_{i = 1}^k {{w_i}} {x_i},\quad \hat y = \sum\limits_{i = 1}^k {{w_i}} {y_i}.$ | (10) |
以上为整体的DD-WKNN算法描述.
2.2 定位实现流程定位的实现基于三个步骤:位置指纹库的采集和聚类,对测量点位置的估计.
在指纹库的采集和聚类阶段,需要对选定的已知位置锚节点进行坐标测量,然后对该点多次测量各个无线接入点的RSSI值,求得平均值作为该点的离线位置指纹数据;按照上述方法对多个锚节点进行上述测量,将各个锚节点的离线位置指纹数据依次录入数据库.然后利用K-means算法对全部获得的离线指纹数据进行聚类,得到特征相似的位置指纹数据聚类.
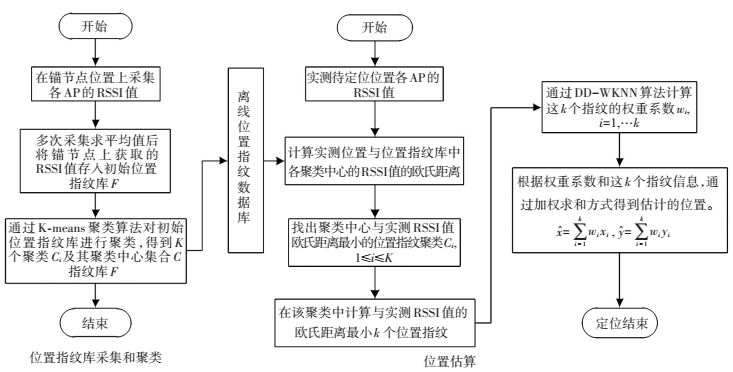
在位置估计阶段,首先将实测点坐标上测得的各个无线接入点的RSSI值与离线位置指纹数据库中的聚类质心RSSI值相比较,选取与离线指纹聚类质心欧氏距离最短的聚类.然后在该聚类中计算各个锚点RSSI值与实测RSSI值的欧氏距离,选取K个欧氏距离最短的锚节点数据.利用改进的WKNN算法估算出实测数据点的位置.整体定位实现流程如图 1所示.
|
图 1 基于DD-WKNN算法的定位流程 Figure 1 The locating process based on DD-WKNN |
分别对基于K-means的位置指纹库数据聚类和实测值位置估计两方面对DD-WKNN算法时间复杂度进行分析. K-means算法的时间复杂度上界为Ocluster(n*K*t),其中n为位置指纹库中指纹数据的个数,K为需要聚类的类个数,t为迭代次数.当n和K一定时,算法迭代次数越多,聚类需要的计算量越大,此时聚类结果更精确.一般来说,为了得到较为可靠定位数据时需要迭代次数大于100次.但该聚类工作是建立位置指纹库过程的一部分,在对实测数据进行定位时并不需要重复计算,因此带来的计算量增加成本可以无需考虑.并且位置指纹数据经过聚类后,在实测数据与位置指纹数据进行比对时,仅仅需要与K个聚类的聚类中心进行比对,所需的比对计算量是减少的,相对于将实测数据与全部位置指纹数据进行比对的算法,需要比对的数据数量减少了n-K-k个,其中k为参考位置指纹个数.在对k个参考位置指纹数据进行处理时,以经典欧氏距离WKNN算法作对比,欧氏距离WKNN计算K个数据与实测数据的欧氏距离,DD-WKNN计算K个数据的变异系数,这两种算法的计算量相当.
综上所述,该算法在位置指纹库建立阶段需要计算量较大,但在实测数据与位置指纹数据比对时计算量小,位置估算阶段计算量与经典欧氏距离WKNN相当.一般情况关注的是定位计算量,因此DD-WKNN算法具有实际应用上的优势.
3 实验验证及分析通过实际室内场景对算法性能进行测试,并与其他位置指纹定位算法进行对比,来评估DD-WKNN算法的性能.
3.1 场景及参数设置实验地点选取吉林大学南湖校区一教办公区3楼走廊—可以感知到多个Wi-Fi接入点RSSI值的区域.为体现算法的适应性,不考察无线接入点位置的影响.从该走廊中选取一块2 m*20 m的条状区域,该区域内可以同时获得至少8个未知地点发出的AP信号, 并能够测得其RSSI值.感知无线接入点的设备选用基于android系统的智能手机,型号为MI2SC,在手机上安装Wi-Fi检视仪APP作为无线接入点RSSI值获取工具.采样点选取在测试区域的两条长边上,从起点开始每隔1.5 m设置一个采样点,坐标从 (0, 0)~(20, 0) 和 (0, 2)~(20, 2) 共计28个采样点.在每个采样点对8个无线接入点的RSSI值进行采样,采样20次后求出均值,将各个RSSI数值录入离线位置指纹数据库.根据锚节点数目及算法中参考位置指纹数目的合理性,K-means算法聚类数目K取值为3.虽然智能手机中的Wi-Fi天线参数性能等并不统一,但由于绝大多数定位应用都是将智能手机作为终端,因此本文对天线带来的影响不作考虑.同时在一般室内环境中,各个房间人员走动、房间门的开关对AP的RSSI值也会带来一定影响,但一般室内定位应用场景中也会具有同样问题,因此虽然在离线位置指纹数据采集过程中对指纹数据进行多次采样求平均值,但本文对该环境影响也不作考虑.
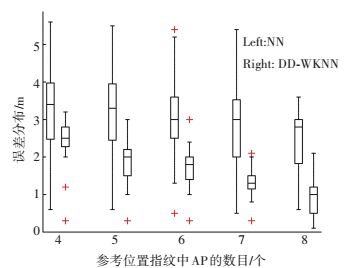
3.2 无线接入点数目对定位误差的影响从8个无线接入点信息中选取4~8个无线接入点的离线位置指纹数据进行定位,对比算法为NN算法.每间隔1 min定位一次.实测定位点坐标从 (0, 1) 到 (20, 1),间隔1 m,共定位21次.统计定位结果误差分布如图 2所示,每组数据左侧为NN算法,右侧为DD-WKNN算法.
|
图 2 位置指纹中无线接入点数目对算法的影响 Figure 2 The number of APs in location fingerprints' influence on the algorithm |
从图 2可以看出,随着位置指纹库中参考AP数量的增加,NN算法和DD-WKNN算法定位精度皆有不同程度的增加,说明参考AP数量对于位置指纹定位具有一定的影响,且为正相关.同时通过观察每组数据可知,在相同参考AP数量的前提下,DD-WKNN算法定位精度较NN算法大,且定位误差波动较小,说明DD-WKNN算法在本实验环境中定位性能要优于NN算法.
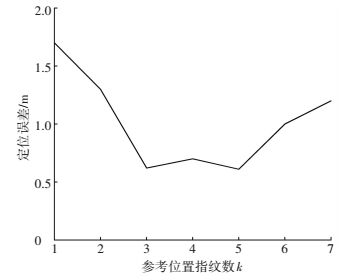
3.3 参考位置指纹数目k对定位误差的影响采用DD-WKNN算法,选取8个无线接入点RSSI值作为离线位置指纹数据,分别在参考位置指纹数目K取值为1~7的情况下进行测试对比,选取21个采集点的均方根误差平均值作为误差平均值,得出结果如图 3所示.
|
图 3 参考位置指纹数目对定位结果的影响 Figure 3 The number of reference point's influence on location results |
由图 3可以看出,K取值在低于3时误差较大,说明参考位置指纹数目少时定位信息不足,定位精度容易受到单个参考位置指纹的影响而产生误差.在K取值为3~5时定位精度较好,说明在参考位置指纹数目适当时,DD-WKNN算法能够达到较高的定位精度.而在K取值大于5时定位误差又开始增大,这是由于过多的参考位置指纹中,部分指纹信息与实测采样值的偏差较大,容易带来不必要的影响,而且这种情况也会增大算法的计算量.
根据实际测试结果,K值在取3时能达到较好的定位精度,同时算法的计算量适中.
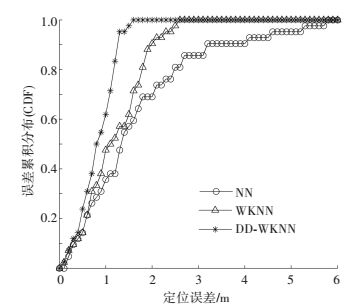
3.4 与现有算法的性能比较选取NN,欧氏距离WKNN与本文提出的DD-WKNN算法进行性能比较,分别在测试区域的 (0, 0.5)~(20, 0.5) 和 (0, 1.5)~(20, 1.5) 坐标点之间每间隔1 m进行RSSI值采集及定位,共计42个实测采集点.每个采样点对各无线接入点RSSI值采集10次,采集间隔1 min,最终结果取10次采集值的均值,将其定位结果与实际位置进行比较,分析误差. 图 4为各算法的误差累积概率分布图.
|
图 4 三种算法的实测性能比较 Figure 4 The measured performance comparison of three algorithms |
从图 4的实测比较结果可以看出:NN算法定位误差较大,误差累积函数收敛最慢,且其最大误差值也较大;传统WKNN算法的定位精度优于NN算法,最大误差值在2.5 m左右;DD-WKNN算法定位精度最优,误差累积函数收敛最快,且最大定位误差值在1.6 m左右.因此,本文提出的DD-WKNN算法在定位精度和误差波动范围上皆具有优势.
4 结论DD-WKNN算法将K个与待定位位置实测Wi-Fi热点RSSI值欧氏距离最接近的位置指纹数据作为位置估计的参照位置,以参考的位置指纹数据离散度作为权重系数的依据,利用WKNN算法的思想对K个位置指纹数据进行加权求和,对待定位位置进行估计.通过实际场景的测试表明,该算法在定位精度上优于原有的以欧氏距离作为权重系数的WKNN算法,且误差波动较小.同时实验表明参考位置指纹数目k对本算法的定位精度有一定影响,在K取值为3~5时定位精度高,而且此时算法计算量适中.
| [1] |
李德毅, 张天雷, 黄立威. 位置服务:接地气的云计算[J].
电子学报, 2014, 42(4): 786-790.
LI Deyi, ZHANG Tianlei, HUANG Liwei. A down-to-earth cloud computing: location-based service[J]. Acta Electronic Sinica, 2014, 42(4): 786-790. DOI: 10.3969/j.issn.0372-2112.2014.04.025 |
| [2] | JUNGLAS I A, WATSON R T. Location-based services[J]. Communications of the ACM, 2008, 51(3): 65-69. DOI: 10.1145/1325555.1325568 |
| [3] |
李建坡, 钟鑫鑫, 徐纯. 无线传感器网络动态节点定位算法综述[J].
东北电力大学学报, 2015, 35(1): 53-58.
LI Jianpo, ZHONG Xinxin, XU Chun. Review of dynamic node localization algorithm for wireless sensor networks[J]. Journal of Northeast Dianli University, 2015, 35(1): 53-58. |
| [4] |
李建坡, 钟鑫鑫, 徐纯. 无线传感器网络静态节点定位算法综述[J].
东北电力大学学报, 2015, 35(2): 73-82.
LI Jianpo, ZHONG Xinxin, XU Chun. Review of statics node localization algorithm for wireless sensor networks[J]. Journal of Northeast Dianli University, 2015, 35(2): 73-82. |
| [5] | HE S, CHAN S H G. Wi-Fi fingerprint-based indoor positioning: recent advances and comparisons[J]. IEEE Communications Surveys & Tutorials, 2016, 18(1): 466-490. DOI: 10.1109/COMST.2015.2464084 |
| [6] | 杨铮, 吴陈沭, 刘云浩. 位置计算:无线网络定位与可定位性[M]. 北京: 清华大学出版社, 2014: 113-115. |
| [7] | GEZICI S. A Survey on wireless position estimation[J]. Wireless Personal Communications, 2008, 44(3): 263-282. DOI: 10.1007/s11277-007-9375-z |
| [8] | BAHL P, PADMANABHAN V N. RADAR: an in-building RF-based user location and tracking system[C]// Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies. Tel Aviv: IEEE Press, 2000:775-784. |
| [9] | CHAN E C L, BACIU G, MAK S C. Using Wi-Fi signal strength to localize in wireless sensor networks[C]// WRI International Conference on.Kuming: IEEE Computer Society, 2009:538-542. |
| [10] | WU D, XU Y, MA L. Research on RSS based indoor location method[C]// Knowledge Engineering and Software Engineering 2009. Shenzhen: IEEE, 2009:205-208. |
| [11] | MADIGAN D, EINAHRAWY E, MARTIN R P, et al. Bayesian indoor positioning systems[C]// Proceedings IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies. Miami: IEEE Press, 2005:1217-1227. |
| [12] | DAWES B, CHIN K W. A comparison of deterministic and probabilistic methods for indoor localization[J]. Journal of Systems & Software, 2011, 84(3): 442-451. DOI: 10.1016/j.jss.2010.11.888 |
| [13] |
徐玉滨, 邓志安, 马琳. 基于核直接判别分析和支持向量回归的WLAN室内定位算法[J].
电子与信息学报, 2011, 33(4): 896-901.
XU Yubin, DENG Zhian MA Lin. WLAN Indoor positioning algorithm based on KDDA and SVR[J]. Journal of Electronics & Information Technology, 2011, 33(4): 896-901. DOI: 10.3724/SP.J.1146.2010.00813 |
| [14] |
朱明强, 侯建军, 刘颖, 等. 基于尺度优化IUKF滤波的室内定位估计方法[J].
北京邮电大学学报, 2013, 36(4): 65-70.
ZHU Mingqiang, HOU Jianjun, LIU Ying, et al. Indoor localization estmation based on scaled iterated unscented Kalman filter[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(4): 65-70. DOI: 10.13190/jbupt.201304.66.049 |
| [15] |
陈淼. 基于多高斯混合模型的WLAN室内定位系统[J].
华中科技大学学报 (自然科学版), 2012, 40(4): 67-71.
CHEN Miao. WLAN indoor location system based on multi-Gaussian mixture model[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(4): 67-71. DOI: 10.13245/j.hust.2012.04.019 |
| [16] |
韦燕华, 周彦, 王冬丽. 基于LS-SVM的位置指纹室内定位[J].
计算机工程与应用, 2016, 52(9): 122-125.
WEI Yanhua, ZHOU Yan, WANG Dongli. Location fingerprints based indoor positioning using least squares support vector machines[J]. Computer Engineering and Applications, 2016, 52(9): 122-125. DOI: 10.3778/j.issn.1002-8331.1402-0208 |
 2017, Vol. 49
2017, Vol. 49


