2. 结构风工程与城市风环境北京市重点实验室 (北京交通大学), 北京 100044;
3. 北京首钢园林绿化有限公司, 北京 100041
2. Beijing's Key Laboratory of Structural Wind Engineering and Urban Wind Environment (Beijing Jiaotong University), Beijing 100044, China;
3. Beijing Shougang landscape Co., Ltd., Beijing 100041, China
为满足零换乘和交通流线的立体化,现代大型铁路客运站普遍采用“房桥合一”结构体系[1],与传统结构相比, 具有设计跨度大、振动荷载类型多、功能分区明确与振动响应明显的特点.人群、列车和大型设备多种荷载作用下,结构动力响应会对旅客心理与生理活动造成干扰[2],采用传统舒适度评价标准判断“房桥合一”结构的舒适性并不合适.
1828年英国土木工程协会的Tomas Tredgold指出:为避免楼盖振动导致的不便,需足够大的梁高[3].文献[4]通过实验室研究人对楼盖竖向振动的主观反应,提出了舒适度相关标准.文献[5]指出目前主要通过频率调整法和限制动力响应法保证结构振动的舒适度,其中ISO 2631/2、BS 6472与GB 10070—88等标准均采用限制动力响应法进行舒适度评价[6-9],即只要工程结构的加速度指标不超过标准限值,便满足舒适度要求.文献[10-11]基于心理物理学原理建立了烦恼率计算模型,考虑了人主观反应判断的模糊性与对振动刺激感受的随机性,能够定量评价结构振动引起的烦恼率.文献[12-13]分别采用烦恼率模型针对人行桥及汽车的舒适性做了相应评估.然而,对于类似铁路客运站等使用功能较为复杂的建筑结构的定量舒适度评价研究较少.
本文针对某大型铁路客站进行人群与列车荷载下的现场动力测试,获得了“房桥合一”结构正常运营下的振动强度分布资料,通过旅客对振动的主观反应调研,获得了该振动强度下的实际烦恼率.实测数据资料,结合已有烦恼率计算模型从根本上建立考虑荷载类型与结构跨度的振动容许下限值,进而计算不同使用功能区域的烦恼率曲线,为现行舒适度评价标准针对结构形式与使用功能作相应修订提供参考.
1 舒适度评价指标与标准舒适感指人在绝大部分时间内感受不到建筑物的振动[14],舒适度为其程度,通常用“非常舒适”到“非常不舒适”等一系列程度逐渐增强的语言描述, 大量测试与实验室研究将振动反应主观描述与振动强度建立关系,舒适度评价以振动响应是否超出标准限值来判断, 一般使用峰值加速度和均方根加速度作为评价依据, 当波峰因数大于9时,采用最大瞬态振动值MTVV和振动剂量VDV评价.
均方根加速度、MTVV与VDV定义为:
| ${{a}_{\text{w}}}={{\left[\frac{1}{T}\int_{0}^{T}{a_{\text{w}}^{2}\left( t \right)\text{d}t} \right]}^{\frac{1}{2}}}, $ | (1) |
| $\text{MTVV=max}\left[{{\left\{ \frac{1}{\tau }\int_{{{t}_{0}}-r}^{{{t}_{0}}}{{{\left[{{a}_{\text{w}}}\left( t \right) \right]}^{2}}\text{d}t} \right\}}^{\frac{1}{2}}} \right], $ | (2) |
| $\text{VDV=}{{\left[\int_{0}^{T}{{{\left[{{a}_{\text{w}}}\left( t \right) \right]}^{4}}\text{d}t} \right]}^{\frac{1}{4}}}.$ | (3) |
式中:T为振动信号持续时间长度,s;τ为运行平均积分时间,建议取1 s,aw(t) 为通过频率加权函数w(f) 计权后的振动信号加速度,m/s2.
不同国家舒适度标准采用不同评价指标,部分指标之间可相互转换,表 1给出各国振动标准及对应舒适度评价指标.
| 表 1 舒适度标准与评价指标 Table 1 Comfortable standard and evaluation index |
中国和日本采用Z振级 (dB) 作为评价指标:
| $V{{L}_{\text{Z}}}=20\ \log \left( {{a}_{\text{w}}}/{{a}_{0}} \right), $ | (4) |
式中:VLZ为Z振级,aw为加权均方根加速度,a0为基准加速度,ISO 2631规定取值10-6 m/s2.
传统舒适度评价时,将评价场所的振动信号带入上述公式计算相应的指标值,若评价指标值未超出标准限值,说明该评价场所满足舒适度要求,但只能得到“舒适”或“不舒适”、满足规范要求与不满足要求等半定量结论.
2 烦恼率基本概念与计算方法某一振动作用下,产生烦恼反应或感到振动不可接受的人数占统计总人数的比例即为烦恼率.烦恼率模型以主要评价标准和评价方法为数据基础和依据,其理论基础为心理物理学的信号检测理论,结合运用模糊数学原理与概率统计理论.舒适度标准规定的限值在一定水平上是人为划分的,结构振动水平高于容许限值时,并非所有人都认为振动不可接受,实验结果表明人对振动感受具有随机性且主观判断具有模糊性,尽管结构振动水平低于容许限值,依然存在一部分人觉得振动不可接受.
文献[15]在人对振动主观感受程度差异性方面进行了实验室研究,以均方根加速度为1 m/s2,频率为16 Hz的振动信号作为参考信号,用频率为4 Hz的振动信号作为比较信号,逐步增强比较信号的RMS,当振感刚好超过16 Hz信号的振感时,记录并统计比较信号的RMS,其为连续性分布,可以用对数正态分布描述,计算表达式见式 (5).并且文献[15]指出“Griffin得到的变异系数为0.3,Magid认为其值为0.1,而Forthergill则认为是0.5”.文献[14]拟合了3种系数下的烦恼率曲线,发现变异系数对结果的影响可忽略.
| $f\left( x\left| u \right. \right)=\frac{1}{\sqrt{2\pi }u\sigma }\exp \left( \frac{-{{\left( \ln \left( u \right)-{{\mu }_{\ln \left( x \right)}} \right)}^{2}}}{2{{\sigma }^{2}}} \right), $ | (5) |
式中
| $\begin{align} & A\left( x \right)=\int_{{{u}_{\min }}}^{\infty }{f\left( x\left| u \right. \right)v\left( u \right)\text{d}u}= \\ & \ \ \ \ \ \ \ \ \ \ \ \int_{{{u}_{\min }}}^{\infty }{\frac{1}{\sqrt{2\pi }\sigma u}\exp \left( \frac{-{{\left( \ln \left( u/x \right)+0.5{{\sigma }^{2}} \right)}^{2}}}{2{{\sigma }^{2}}} \right)v\left( u \right)\text{d}u.} \\ \end{align}$ | (6) |
式中:v(u) 为概念隶属度函数,服从心理物理学上的Fechner律,如式 (7) 所示,umin为容许振动下限值,umax为容许振动上限值,a、b为待定系数,可由实验数据或规范计算得到.
| $v\left( u \right)=\left\{ \begin{align} & \ \ \ \ \ \ \ 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ u < {{u}_{\min }}; \\ & a\ln \left( u \right)+b, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{u}_{\min }}\le u\le {{u}_{max}}; \\ & \ \ \ \ \ \ \ 1, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ u>{{u}_{max}}. \\ \end{align} \right.$ | (7) |
“房桥合一”结构高架站厅设计跨度大,自振频率低,与人行频率较接近,当分布大量人群时更容易引起结构的振动响应;尽管列车荷载引起的结构振动频率高,但轮轨作用力造成直接冲击作用.本文以某个典型的“房桥合一”结构体系的大型铁路客站为研究对象,进行了人致结构振动实测,获取整个站厅在人群荷载下的振动响应;结构模型施加列车荷载进行动力分析,指导现场试验方案布置,获取了关键位置的车致结构动力响应.
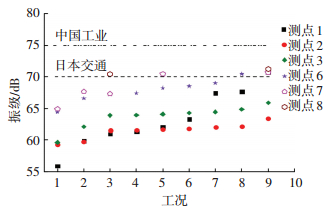
对两种荷载下的结构舒适度进行评价,参照规范及限值见表 2,人群荷载下的结构振动响应转换成加权Z振级指标,参照中国和日本规范;提取直通列车作用下的峰值加速度,对比ISO与美国规范,见图 1~4.
| 表 2 评价标准及限值 Table 2 Evaluation standards and limits |
|
图 1 人致结构Z振级与标准限 Figure 1 Human-induced vibration of Z andstandard limit |
|
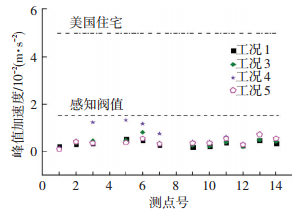
图 2 B区车致峰值加速度与标准限值 Figure 2 B vehicle-induced peak acceleration and standard limit |
|
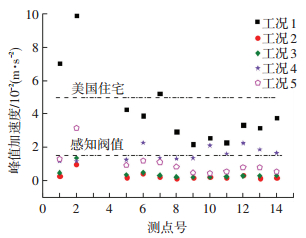
图 3 A区车致峰值加速度与标准限值 Figure 3 A vehicle-induced peak acceleration and standard limit |
|
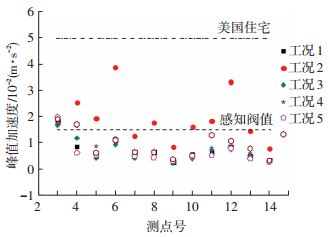
图 4 C区车致峰值加速度与标准限值 Figure 4 C vehicle-induced peak acceleration and standard limit |
图 1显示,只有部分测点工况的振动强度超出了日本限值,与中国标准仅相差3 dB,几乎要超出标准限值;然而,基于人对振动的主观反应调研,实际烦恼率仅为2%;图 2表明,局部区域的车致振动峰值加速度均未达到人体对振动的感知阀限,其烦恼率的理论值为0,而实际烦恼率值为2%;图 3、4显示部分测点超出了感知阀值和美国住宅限值,实际烦恼率为10%.传统评价方法将振动响应指标与舒适度标准进行对比评价,只能简单的给出是否符合舒适度标准要求,不能将实际烦恼率量值化,无法评价建筑物舒适度的优劣,而且“房桥合一”属于新型结构形式,其舒适度评价是否应该继续使用原标准限值存在争议.
4 “房桥合一”结构烦恼率分析 4.1 “房桥合一”结构烦恼率参数将式 (7) 代入 (6),对u积分便可得到烦恼率关于实际振动强度x的函数表达式,给出场所的任意振动强度均可求出相应的烦恼率值.而求取待定系数a、b的关键是引用实验数据和规范资料,确定容许振动上下限umax、umin,国家标准制定不同使用场所的振动容许上下限时,均在基本舒适度曲线r0的基础上乘以一定系数,ISO 2631-2给出了不同地点的舒适度上下限,即r0放大系数,见表 3.
| 表 3 ISO 2631-2采用的加速度放大倍数 Table 3 ISO 2631-2 magnification of acceleration |
竖向振动r0=5×10-3 m/s2,水平向振动r0=3.6×10-3 m/s2,以要求严格区域竖向振动为例,umin=5×10-3 m/s2,umax=2×10-2 m/s2,根据式 (7) 可得
| $\left\{ \begin{array}{l} a\ln \left( {{u_{\min }}} \right) + b = 0\\ a\ln \left( {{u_{\max }}} \right) + b = 1 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} a = 0.7213\\ b = 3.8219 \end{array} \right.$ |
规范给出要求严格区域、住宅、办公室及车间评价场所的振动上下限值,但是“房桥合一”结构从结构形式与荷载类型上,均与上述场所存在一定差异,并不适合直接引用其数据资料,不妨设定其振动容许上下限分别为r2、r1,国际标准ISO 2631表明同一地点及时间的容许上下限存在r2=4r1的规律,对于“房桥合一”结构,其待定系数a、b为
| $\left\{ \begin{array}{l} a\ln \left( {{r_1}} \right) + b = 0\\ a\ln \left( {{r_2}} \right) + b = 1 \end{array} \right.\left\{ \begin{array}{l} a = 0.7213\\ b = - 1.3864\ln \left( {{r_1}} \right) \end{array} \right.$ |
将铁路客站的振动强度x的概率分布绘制成图 5~7,人群荷载下主梁跨度为40.5 m区域为集中坐席区,列车荷载下主梁跨度为40.5 m区域为直通列车候车区,而主梁跨度为32 m区域为客流通道及贵宾室,分为AC左右两个区域.以振动强度与出现概率相对较高能够反映高架站厅常态振动水平为原则,选取中心振级作为不同使用功能区域的振动强度.

|
图 5 直通列车候车区振动强度分布 Figure 5 Vibration intensity distribution of train waiting area |
|
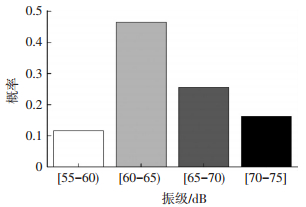
图 6 集中坐席区振动强度分布 Figure 6 Vibration intensity distribution of designated waiting area |
|
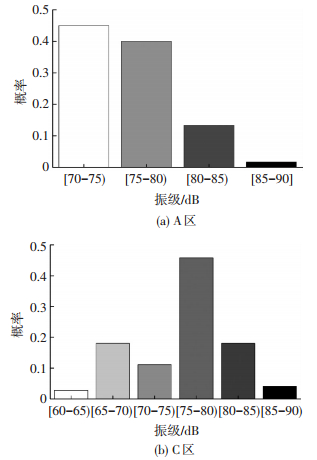
图 7 客流通道及贵宾室振动强度分布 Figure 7 Vibration intensity distribution of Passenger flow channel and VIP rooms |
为获得旅客对大跨度站厅振动效应的主观反应,设计了考虑年龄、性别、姿态等多重因素的调研问卷,并获得544份有效调研结果.基于模糊数学评价理论,对所获调研数据进行分类统计处理,获得了高架站厅不同功能区域的烦恼率值A (x),将功能分区的振动强度与实际烦恼率值绘制成表 4.
| 表 4 站厅振动强度与烦恼率分布 Table 4 Vibration intensity and annoyance rate distribution in hall |
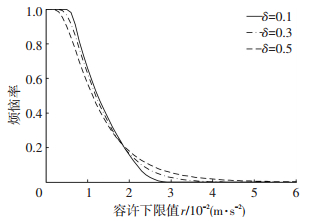
表 4给出不同功能分区的振动强度x及烦恼率值A(x),结合概念隶属度函数,对式 (6) 逆运算可得“房桥合一”结构不同功能区域的烦恼率-振动容许下限值曲线,见图 8~10.
|
图 8 88 dB烦恼率-容许下限值曲线 Figure 8 Annoyance rate-allowable limit curve of 88 dB |
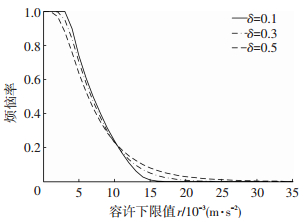
|
图 9 83 dB烦恼率-容许下限值曲线 Figure 9 Annoyance rate-allowable limit curve of 83 dB |

|
图 10 73 dB烦恼率-容许下限值曲线 Figure 10 Annoyance rate-allowable limit curve of 73 dB |
3种变异系数下的结果差异并不大,因此本文选取变异系数为0.3,根据烦恼率—振动容许下限值曲线计算得到不同区域的振动容许下限值r1及振动限值,见表 5.与原标准限值对比可知,“房桥合一”结构限值要求相对没有那么严格,仅人群荷载下的限值为75 dB,基于不同结构跨度与使用功能,局部区域振动限值为82 dB与90 dB.尽管该类结构的设计跨度大,振动响应明显,但环境较为嘈杂,旅客对舒适度的要求相对降低.
| 表 5 “房桥合一”容许下限及振动限值 Table 5 Permissible lower limit and vibration limits of "Building-Bridge integration" |
基于“房桥合一”结构体系的现场动力测试与旅客对振动效应主观反应的调研,结合连续性分布的烦恼率模型,推导演算出不同功能分区的新容许振动下限值r1,进而给定新的振动限值.此限值可用来指导该类结构体系的工程设计,确保结构安全性的前提下,保证其舒适度要求,满足建筑结构设计的经济性要求.但限值仅简单的评价结构是否满足要求,并不能将任意振动强度下的烦恼率进行定量,通过建立的新容许下限值及方程组 (7) 得到概念隶属度系数a、b,进一步结合式 (6) 建立关于“房桥合一”结构的烦恼率曲线,计算结果见表 6.不同功能分区烦恼率曲线见图 11~13.
| 表 6 “房桥合一”结构烦恼率曲线计算结果 Table 6 Annoyance rate curve calculation results of "Building-Bridge Integration" structure |
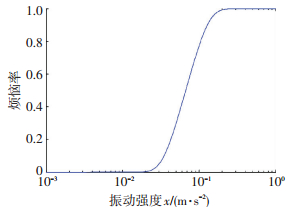
|
图 11 直通列车候车区烦恼率曲线 Figure 11 Annoyance rate curve of transit train waiting room |
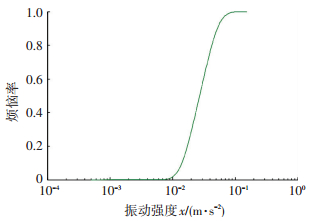
|
图 12 客流通道与贵宾室烦恼率曲线 Figure 12 Annoyance rate curve of passageway and VIP room |
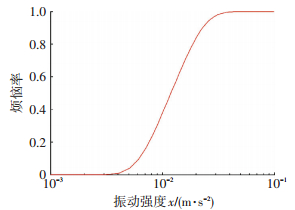
|
图 13 集中坐席区烦恼率曲线 Figure 13 Annoyance rate curve of seating area |
由烦恼率曲线可得振动限值x对应的烦恼率值为7×10-2左右,即结构振动强度达到振动限值时室内7%的旅客受到干扰反应,振动强度为2x时,烦恼率为47%,4x下的烦恼率为89.9%,结果与振动舒适度标准对于不同振动水平下人的主观反应描述较为一致.
5 结论1) 连续分布的烦恼率模型考虑了人对振动主观反应判断的模糊性及振动刺激感受的随机性,并能将任意振动强度下的烦恼率量值化,对于工程结构的舒适度评价更有意义.该方法具有普遍适用性,也可用于其他类型结构的舒适度评价.
2)“房桥合一”新型结构体系在人群荷载、直通列车荷载作用下的振动强度及峰值加速度基本上没有超出标准限值,然而人对振动主观反应的调研结果表明不同区域的烦恼率为2%、10%,说明现有规范并不适合直接评价该类新型结构的舒适性,需建立新的振动限值范围.
3) 基于已有的考虑了心理物理学的烦恼率模型与实测数据资料建立了该类结构体系新的容许振动下限值r1,其对应的新振动限值分别为90、82、75 dB,该类结构振动限值范围为75~90 dB,相对传统标准限值而言要求适当降低,其原因在于尽管结构的设计跨度大,振动响应明显,但是环境较为嘈杂,旅客对舒适度的要求相对降低.
4) 根据新容许振动下限值建立的相应烦恼率曲线,可评估任意振动强度下产生干扰反应的人群比例.振动强度为r1时,对应的烦恼率值为7%;振动强度为2r1时,对应的烦恼率值为47%;振动强度为4r1时,对应烦恼率值为89.9%,以上结果与舒适度标准对于不同振动水平下人的主观反应描述较为一致,其为满足舒适度要求与经济性要求的建筑结构设计提供新的参考.
| [1] |
盛平, 王轶, 张楠, 等. 大型站桥合一客站建筑的舒适度研究[J].
建筑结构, 2009, 39(12): 43-45.
SHENG Ping, WANG Yi, ZHANG Nan, et al. Study of vibration comfort of a bridge-station combined railway station[J]. Building Structure, 2009, 39(12): 43-45. |
| [2] |
罗仕鉴. 基于生物学反应的驾驶舒适度研究[D]. 杭州: 浙江大学. 2005: 30-43.
LUO Shijian.Study on driving comfort based on biologicalresponse[D].Hangzhou:Zhejiang University. 2005: 30-43. |
| [3] | ALLEN D E, PERNICA G. Control of floor vibration[M]. Ottawa: Institute for Research in Construction, 1998: 1-4. |
| [4] | Steed design guide 11.Floor vibrations due to human activity[S].Chicago:American Institute of Steel Construction, 1997. |
| [5] |
孙利民, 闫兴非. 人行桥人行激励振动及设计方法[J].
同济大学学报 (自然科学版), 2004, 32(8): 996-999.
SUN Limin, YAN Xingfei. Human walking induced footbridge vibration and its serviceability design[J]. Journal of Tong Ji University (Natural Science), 2004, 32(8): 996-999. DOI: 10.3321/j.issn:0253-374X.2004.08.004 |
| [6] | Evaluation of human exposure to whole-body vibration-continuous and shock-induced vibration in buildings: ISO2631-2[S].Switzerland:International Standard organization, 1989. |
| [7] | GULVANESSIAN H. EN1990 Euro code-Basis of structural design[C]//Proceedings of the ICE-Civil Engineering. London:Thomas Telford, 2001, 144(6):8-13.DOI:10.1680/cien.2001.144.6.8. |
| [8] | British Standard 6472.Guide to evaluation of human exposure to vibration in buildings (1 Hz to 80 Hz) [S]. London: British Standard Institute, 1992. DOI: 10.3403/19971044U. |
| [9] |
城市区域环境振动标准: GB 10070-88 [S]. 北京: 国家环境保护局, 1989.
Standard of vibration in urban area environment:GB 10070-88[S].Beijing:National Environmental Protection Agency, 1989. |
| [10] |
宋志刚, 金伟良. 振动建筑中人的烦恼率[J].
强度与环境, 2002, 29(4): 51-58.
SONG Zhigang, JIN Weiliang. The annoyance rate in a vibrating building[J]. Structure & Environment Engineering, 2002, 29(4): 51-58. DOI: 10.3969/j.issn.1006-3919.2002.04.008 |
| [11] |
宋志刚, 金伟良. 基于海冰区划的平台结构振动舒适度设计--容许加速度限值[J].
海洋工程, 2005, 23(2): 61-65.
SONG Zhigang, JIN Weiliang. Serviceability design of ice-induced platform vibration based on ice zoning map of Bohai Sea-Acceptable acceleration levels[J]. The Ocean Engineering, 2005, 23(2): 61-65. |
| [12] |
法永生, 李东, 孙翠华. 人行桥随机人行荷载下的振动分析及其舒适度评价的新方法[J].
振动与冲击, 2008, 27(1): 119-123.
FA Yongsheng, LI Dong, SUN Cuihua. Footbridge vibration analysis of stochastic pedestrian loads and the new method for evaluating[J]. Journal of Vibration and Shock, 2008, 27(1): 119-123. DOI: 10.3969/j.issn.1000-3835.2008.01.027 |
| [13] |
唐传茵, 张天侠, 李华, 等. 汽车振动舒适性评价研究[J].
振动与冲击, 2008, 27(9): 158-161.
TANG Chuanyin, ZHANG Tianxia, LI Hua, et al. Evaluation of ride comfort of a vehicle[J]. Journal of Vibration and Shock, 2008, 27(9): 158-161. DOI: 10.3969/j.issn.1000-3835.2008.09.038 |
| [14] |
宋志刚. 基于烦恼率模型的工程结构振动舒适度设计新理论[D]. 杭州: 浙江大学, 2003.
SONG Zhigang. A new annoyance-based vibration comfort design theory on engineering structures[D]. Hangzhou: Zhejiang University, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10335-2003041652.htm |
| [15] | GRIFFIN M J. Handbook of human vibration[M]. London: Academic Press, 1994: 90-92. |
 2017, Vol. 49
2017, Vol. 49


