引用本文

刘延芳, 刘宏, 孟瑶. 负载不确定的柔性机械臂自适应自抗扰控制[J]. 哈尔滨工业大学学报, 2017, 49(7): 12-19. DOI: 10.11918/j.issn.0367-6234.201605064. 复制到剪切板

LIU Yanfang, LIU Hong, MENG Yao. Adaptive active disturbance rejection control of flexible manipulators[J]. Journal of Harbin Institute of Technology, 2017, 49(7): 12-19. DOI: 10.11918/j.issn.0367-6234.201605064. 复制到剪切板

基金项目

中国博士后科学基金(2014M560255)；机器人技术与系统国家重点实验室开放研究项目(SKLRS-2013-ZD-05)；黑龙江省博士后基金(LBH-Z14107)

作者简介

刘延芳(1986—)，男，博士，讲师;
刘宏(1966—), 男，长江学者特聘教授，博士生导师

通信作者

刘延芳，lyf04025121@126.com

文章历史

收稿日期: 2016-05-16

Abstract Full text Figures/Tables PDF

负载不确定的柔性机械臂自适应自抗扰控制

刘延芳^1,2, 刘宏¹, 孟瑶³

1. 机器人系统与技术国家重点实验室(哈尔滨工业大学)，哈尔滨 150001;
2. 哈尔滨工业大学航天工程系，哈尔滨 150001;
3. 上海宇航系统工程研究所，上海 201109

收稿日期: 2016-05-16

基金项目: 中国博士后科学基金(2014M560255)；机器人技术与系统国家重点实验室开放研究项目(SKLRS-2013-ZD-05)；黑龙江省博士后基金(LBH-Z14107)

作者简介: 刘延芳(1986—)，男，博士，讲师;
刘宏(1966—), 男，长江学者特聘教授，博士生导师

通信作者: 刘延芳，lyf04025121@126.com

摘要: 为解决末端具有不确定负载的柔性机械臂的位置控制问题，设计了自适应自抗扰控制器.采用奇异摄动理论将多柔性连杆机械臂动力学系统分解为快时标和慢时标两个子系统.针对快时标子系统设计线性二次型控制器，用于快速抑制柔性连杆的振动，将快时标状态变量转移到慢流形上; 针对慢时标子系统，设计自抗扰控制器，用于跟踪期望角度.针对末端负载的不确定性，采用迭代最小二乘算法估计末端负载的质量, 并在自抗扰控制器中进行补偿.结果表明：末端负载的不确定量达到预估负载质量的200%时，在15 rad/s范围内，角度控制的均方差0.08 rad，明显优于不对末端负载进行补偿的情况.在末端负载和机械臂运动速度都发生变化时，所提出的自适应自抗扰控制器具有一定的鲁棒性.

关键词: 多柔性连杆机械臂自抗扰控制负载不确定性自适应控制迭代最小二乘算法

Adaptive active disturbance rejection control of flexible manipulators

LIU Yanfang^1,2, LIU Hong¹, MENG Yao³

1. State Key Laboratory of Robotics and System (Harbin Institute of Technology), Harbin 150001, China;
2. Dept.of Aerospace Engineering, Harbin Institute of Technology, Harbin 150001, China;
3. Aerospace System Engineering Shanghai, Shanghai 201109, China

Abstract: An adaptive active disturbance rejection control is proposed for flexible manipulators with uncertain payload. The two-time scale model of the multiple-flexible-link manipulator is derived via singular perturbation technique. For the fast subsystem, a linear quadratic regulator controller is designed. It depresses the oscillation of flexible links and drives the states to the slow manifold quickly. For the slow subsystem, an adaptive active disturbance rejection controller is proposed to track the desired angular position. A recursive least-squares algorithm is utilized to estimate the payload mass and compensate for the uncertainty. Simulation results show that the mean squire error is less than 0.08 rad even when the payload uncertainty up to 200% of the pre-estimation of the payload mass, which is superior to the case without compensation for the payload uncertain. Thus, the proposed control scheme guarantees a robust performance in presence of uncertain payload and under different maneuver speeds.

Key words: multiple-flexible-link manipulator active disturbance rejection control payload uncertainty adaptive control recursive least-squares

多柔性连杆机械臂(multiple-flexible-link manipulator, MFLM)由于具有质量轻、惯量低等优点，在未来空间站建设、空间操控和在轨服务等任务中担任着重要的角色^[1-4]，同时也是实现装备制造等产业智能化的重要设备^[5-6].然而，机械臂运动过程中，臂杆的柔性导致振动，影响定位精度; 刚体运动与结构振动高度耦合，呈现出强非线性; 关节驱动力矩需要同时实现关节转动和振动控制，属于欠驱动系统; 负载随着任务不同而不同，存在不确定性.本文针对采用柔性臂杆的机械臂的角度运动和振动抑制的控制器设计问题开展研究.

内外环的控制器设计是柔性机械臂常用的控制器设计方法.内环通过臂杆弯曲反馈消除其振动，外环采用角度反馈跟踪期望轨迹.比例微分(proportional derivative, PD)、比例微分积分(proportional integral derivative，PID)、自适应算法、积分阻抗技术、广义比例积分等被广泛用于内环和外环的控制器设计^[7-9]; 基因学习算法^[10]、逆模型控制^[11]、力控制^[12]、采用压电元件的主动振动控制^[13]、H_∞控制^[14]等也都在MFLM的控制上得到了一定的应用.由于结构振动相对于关节的刚体转动要快很多，采用奇异摄动理论将整个复杂系统分解为快时标和慢时标两个相对简单的子系统，在柔性关节^[15-18]、柔性臂杆^[19-21]等机械臂的控制中得到了应用.考虑到很难获得MFLM的精确动力学模型，自抗扰控制(active disturbance rejection control，ADRC)^[21-23]通过扩张状态观测器(extended state observer，ESO)扩展一个状态实现对内部和外部干扰的估计和补偿，采用反馈控制器实现一定的鲁棒性能. ADRC通过质量矩阵可以实现系统的自解耦.但是，末端负载的不确定性导致质量矩阵的不确定，引起ADRC的性能下降.频域辨识和模态滤波器广泛用来解决柔性连杆机械臂末端负载的不确定性^[24-26].

本文在对MFLM系统进行时标分解的基础上，内环快时标子系统采用线性二次型(linear quadratic regulator，LQR)控制器，实现振动的快速抑制; 外环慢时标子系统设计了ADRC控制器，同时采用迭代最小二乘(recursive least-squares，RLS)算法实现对末端负载的估计和补偿.

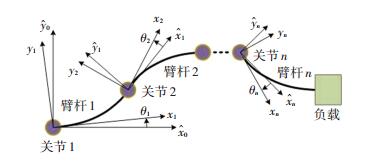
1 系统建模

如图 1所示，MFLM具有n个柔性连杆、n个关节和1个末端负载.臂杆i的长度为l_i，密度为ρ_i，刚度为E_{I_i}; 关节i的驱动力矩为τ_i，角位置记作θ_i.关节认为是集中质量，转动惯量等效到臂杆上，末端负载的质量为m_i.采用Euler-Lagrange方法和假设模态法^{[21, 25]}，得到MFLM的动力学模型为

图 1 MFLM示意 Figure 1 Structure of MFLM

$ \mathit{\boldsymbol{M}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{q}}} \right)\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot \theta }}}\\ {\mathit{\boldsymbol{\ddot q}}} \end{array}} \right] + \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) + \left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{K}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\theta }}\\ \mathit{\boldsymbol{q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\tau }}\\ {\bf{0}} \end{array}} \right], $

(1)

式中：M(θ, q)为质量矩阵，H(θ, ${\boldsymbol{\dot \theta }}$, q, ${\boldsymbol{\dot q}}$)为阻尼力矩矩阵，K为刚度矩阵，θ^T=[θ₁, θ₂, …, θ_n]为角位置矢量，q^T=[q₁^T, q₂^T, …, q_n^T]，q_i^T=[q_i1, q_i2, …, q_im]表示连杆i的模态坐标矢量，q_ij为连杆i的第j阶模态坐标，τ^T=[τ₁, τ₂, …, τ_n]为输入力矩矢量.

把质量矩阵M(θ, q)及其逆矩阵N(θ, q)、H(θ, ${\boldsymbol{\dot \theta }}$, q, ${\boldsymbol{\dot q}}$)进行分解

$ \begin{array}{l} \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{\theta \theta }}}&{{\mathit{\boldsymbol{M}}_{\theta q}}}\\ {\mathit{\boldsymbol{M}}_{\theta q}^{\rm{T}}}&{{\mathit{\boldsymbol{M}}_{\theta q}}} \end{array}} \right],\\ \mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_{\theta \theta }}}&{{\mathit{\boldsymbol{N}}_{\theta q}}}\\ {\mathit{\boldsymbol{N}}_{\theta q}^{\rm{T}}}&{{\mathit{\boldsymbol{N}}_{\theta q}}} \end{array}} \right], \end{array} $

$ \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_\theta }\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)}\\ {{\mathit{\boldsymbol{H}}_q}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)} \end{array}} \right], $

式(1) 可以进一步表示为

$ \begin{array}{l} \mathit{\boldsymbol{\ddot \theta }} = {\mathit{\boldsymbol{N}}_{\theta \theta }}\left( {\mathit{\boldsymbol{\tau }} - {\mathit{\boldsymbol{H}}_\theta }} \right) - {\mathit{\boldsymbol{N}}_{\theta q}}\left( {\mathit{\boldsymbol{K\theta + }}{\mathit{\boldsymbol{H}}_q}} \right),\\ \mathit{\boldsymbol{\ddot q}} = \mathit{\boldsymbol{N}}_{\theta q}^{\rm{T}}\left( {\mathit{\boldsymbol{\tau }} - {\mathit{\boldsymbol{H}}_\theta }} \right) - {\mathit{\boldsymbol{N}}_{qq}}\left( {\mathit{\boldsymbol{K\theta + }}{\mathit{\boldsymbol{H}}_q}} \right). \end{array} $

选择摄动参数为

$ {\mu ^{ - 1}} = \sqrt {{\mu _{\min }}\left( {{\mathit{\boldsymbol{N}}_{qq,0}}\mathit{\boldsymbol{K}}} \right)} , $

其中${\boldsymbol{N}_{qq, 0}} = {\boldsymbol{N}_{qq}}\left| {_{q = 0}} \right.$，μ_min(N_{qq, 0}K)表示q=0且θ在给定的运动范围内变化时矩阵(N_qqK)的最小特征值.利用因子μ²对K进行正则化$\boldsymbol{\tilde K} = {\boldsymbol{\mu} ^2}/\boldsymbol{K}$，同时定义z=q/μ²，将系统(1) 分解为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\ddot \theta }} = {\mathit{\boldsymbol{N}}_{\theta \theta }}\left[ {\mathit{\boldsymbol{\tau }} - {\mathit{\boldsymbol{H}}_\theta }\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{\dot z}}} \right)} \right] - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{N}}_{\theta q}}\left[ {\mathit{\boldsymbol{\tilde Kz + }}{\mathit{\boldsymbol{H}}_q}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{\dot z}}} \right)} \right],\\ {\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{\ddot z = N}}_{\theta q}^{\rm{T}}\left[ {\mathit{\boldsymbol{\tau }} - {\mathit{\boldsymbol{H}}_\theta }\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{\dot z}}} \right)} \right] - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{N}}_{qq}}\left[ {\mathit{\boldsymbol{\tilde Kz + }}{\mathit{\boldsymbol{H}}_q}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{z}},{\mathit{\boldsymbol{\mu }}^2}\mathit{\boldsymbol{\dot z}}} \right)} \right]. \end{array} \right. $

(2)

将μ=0代入并整理，得到慢时标子系统为

$ {{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{s}}} = - \mathit{\boldsymbol{M}}_{\theta \theta ,{\rm{s}}}^{ - 1}{\mathit{\boldsymbol{H}}_{\theta ,{\rm{s}}}}\left( {{\mathit{\boldsymbol{\theta }}_{\rm{s}}},{{\mathit{\boldsymbol{\dot \theta }}}_{\rm{s}}},0,0} \right) + \mathit{\boldsymbol{M}}_{\theta \theta ,{\rm{s}}}^{ - 1}{\mathit{\boldsymbol{\tau }}_{\rm{s}}}. $

(3)

下标‘s’表示慢时标子系统的物理量.

在获得快时标系统时，认为慢时标系统的物理量为常量，定义快时标子系统变量为z_f:=z－z_s，控制量为τ_f:=τ－τ_s, 式(2) 中快时标子系统可以写为

$ \frac{{{{\rm{d}}^2}{\mathit{\boldsymbol{z}}_{\rm{f}}}}}{{{\rm{d}}{\sigma ^2}}} = \mathit{\boldsymbol{N}}_{\theta q}^{\rm{T}}{\mathit{\boldsymbol{\tau }}_{\rm{f}}} - {\mathit{\boldsymbol{N}}_{qq}}\mathit{\boldsymbol{\tilde K}}{\mathit{\boldsymbol{z}}_{\rm{f}}}. $

其中σ=t/μ为快时标标度.

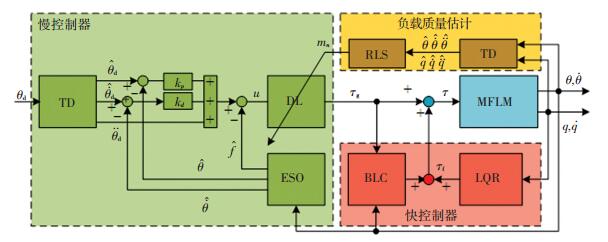
2 控制器设计

图 2给出了控制器结构示意图，控制力矩为

图 2 控制器结构示意图(DL:解耦器, BLC:边界层修正) Figure 2 Composite control scheme DL: Decoupling Law, BLC: Boundary Layer Correction

$ \mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{\tau }}_{\rm{s}}} + {\mathit{\boldsymbol{\tau }}_{\rm{f}}}. $

其中，慢时标控制量τ_s通过ADRC控制器给出，快时标控制量τ_f通过LQR控制器给出，末端负载的质量通过RLS算法估计并反馈至ADRC控制器.

2.1 末端负载的估计

考虑到末段负载的不确定性，将质量矩阵重新表达为两部分

$ \mathit{\boldsymbol{M}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{q}}} \right) = {\mathit{\boldsymbol{M}}_0}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{q}}} \right) + {\mathit{\boldsymbol{C}}_M}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{q}}} \right){m_n}. $

(4)

其中M₀(θ, q)为确定的部分，C_M(θ, q)为不确定负载m_n的贡献系数，是与m_n无关的量.同理，H(θ, ${\boldsymbol{\dot \theta }}$, q, ${\boldsymbol{\dot q}}$)表达为

$ \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) = {\mathit{\boldsymbol{H}}_0}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{C}}_{\rm{H}}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right){m_n}. $

将式4)-5) 带入到式(1) 中可得

$ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}{m_n} = \mathit{\boldsymbol{\eta }}, $

其中：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}} = {\mathit{\boldsymbol{C}}_M}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{q}}} \right)\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot \theta }}}\\ {\mathit{\boldsymbol{\ddot q}}} \end{array}} \right]\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{C}}_{\rm{H}}}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right),}\\ {\mathit{\boldsymbol{\eta = }}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\tau }}\\ {\bf{0}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{K}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\theta }}\\ \mathit{\boldsymbol{q}} \end{array}} \right] - {\mathit{\boldsymbol{H}}_0}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\dot \theta }},\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) - {\mathit{\boldsymbol{M}}_0}\left( {\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{q}}} \right)\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot \theta }}}\\ {\mathit{\boldsymbol{\ddot q}}} \end{array}} \right].} \end{array} $

考虑到在某些情况下, Φ≈0，同时为了充分利用旧数据信息，采用迭代最小二乘算法估计负载质量

$ \begin{array}{l} {{\dot m}_{n,k}} = {{\dot m}_{n,k - 1}} + {\mathit{\boldsymbol{G}}_k}\left( {{\mathit{\boldsymbol{\eta }}_k} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k^{\rm{T}}{{\hat m}_{n,k - 1}}} \right),\\ {\mathit{\boldsymbol{G}}_k} = {P_{k - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}{\left( {\mathit{\boldsymbol{I + \boldsymbol{\varPhi} }}_k^{\rm{T}}{P_{k - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}} \right)^{ - 1}},\\ {P_k} = \left( {1 - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k^{\rm{T}}} \right){P_{k - 1}}. \end{array} $

在应用中，角度信息可以通过编码器测得，臂杆弯曲信息可以通过应变片测量，对于角度的导数和各阶模态坐标需要通过估计得到.这里采用跟踪微分器(tracking differentiator, TD):

$ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = fh\left( {{x_1} - u,{x_2},r,{h_0}} \right). \end{array} \right. $

式中：x₁、x₂是状态变量，u是控制输入，h₀和r分别是滤波因子和速度因子，fh(x₁, x₂, r, h₀)定义如下:

$ \begin{array}{l} d = r{h_0};\\ {d_0} = {h_0}d;\\ y = {x_1} + {h_0}{x_2};\\ {a_0} = \sqrt {{d^2} + 8r\left| y \right|} ; \end{array} $

$ \begin{array}{l} a = \left\{ \begin{array}{l} {x_2} + 0.5\left( {{a_0} - d} \right){\mathop{\rm sgn}} \left( y \right),\;\;\;\left| y \right| > {d_0};\\ {x_2} + y/{h_0},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| y \right| \ge {d_0}; \end{array} \right.\\ fh = - \left\{ \begin{array}{l} r{\mathop{\rm sgn}} \left( a \right),\;\;\;\;\;\left| a \right| > d;\\ ra/d,\;\;\;\;\;\;\;\;\;\left| a \right| \le d. \end{array} \right. \end{array} $

2.2 外环自抗扰控制器

慢时标子系统(3) 可以表达为

$ {{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{s}}} = \mathit{\boldsymbol{f}}\left( \cdot \right) + \mathit{\boldsymbol{u}}, $

(6)

其中

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}\left( \cdot \right) = {{\left[ {\begin{array}{*{20}{c}} {{f_1}\left( \cdot \right)}&{{f_2}\left( \cdot \right)}& \cdots &{{f_n}\left( \cdot \right)} \end{array}} \right]}^{\rm{T}}} = }\\ { - \mathit{\boldsymbol{M}}_{\theta \theta ,{\rm{s}}}^{ - 1}{\mathit{\boldsymbol{H}}_{\theta ,{\rm{s}}}}\left( {{\mathit{\boldsymbol{\theta }}_{\rm{s}}},{{\mathit{\boldsymbol{\dot \theta }}}_{\rm{s}}},0,0} \right)} \end{array} $

表示总的干扰，包含内部不确定性和外部干扰;

$ \mathit{\boldsymbol{u = }}{\left[ {\begin{array}{*{20}{c}} {{u_1}}&{{u_2}}& \cdots &{{u_n}} \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{M}}_{\theta \theta ,{\rm{s}}}^{ - 1}{\mathit{\boldsymbol{\tau }}_{\rm{s}}}, $

(7)

是虚拟控制量.令x_i1=θ_{i, s}、x_i2=${\boldsymbol{\dot \theta }}$_{i, s}，则式(6) 中的第i个子系统可以表达为状态空间的形式

$ \left\{ \begin{array}{l} {{\dot x}_{i1}} = {x_{i2}},\\ {{\dot x}_{i2}} = {f_i}\left( \cdot \right) + {u_i}. \end{array} \right. $

选择虚拟控制为

$ {u_i} = \left( {{{\ddot \theta }_{{\rm{d}}i}} - {{\hat x}_{i3}}} \right) + {k_{{\rm{d}}i}}\left( {{{\dot \theta }_{{\rm{d}}i}} - {{\hat x}_{i2}}} \right) + {k_{{\rm{p}}i}}\left( {{\theta _{{\rm{d}}i}} - {{\hat x}_{i1}}} \right). $

式中：k_pi和k_di分别是比例和微分系数，θ_di、${\dot \theta }$_di、${\ddot \theta }$_di分别是连杆i的期望角度、角速度和角加速度.假设f_i(·)可微，通过扩展状态x_i3=f_i(·)，第i个连杆的角度、角速度和总干扰，即${\hat x_{i1}}$, ${\hat x_{i2}}$和${\hat x_{i3}}$可通过ESO获得:

$ \left\{ \begin{align} & {{{\dot{\hat{x}}}}_{i1}}={{{\hat{x}}}_{i2}}-{{\beta }_{i1}}{{{\hat{e}}}_{i}}, \\ & {{{\dot{\hat{x}}}}_{i2}}={{{\hat{x}}}_{i3}}-{{\beta }_{i2}}{{{\hat{e}}}_{i}}+{{u}_{i}}, \\ & {{{\dot{\hat{x}}}}_{i3}}=-{{\beta }_{i3}}{{{\hat{e}}}_{i}}. \\ \end{align} \right. $

式中：β_i1、β_i2、β_i3是状态估计器增益，${\hat e_i} = {x_{i1}} -{\hat x_{i1}}$为状态x_i1的估计误差.通过将所有的状态估计的极点设计在－ω₀，其特征方程成为Hurwitz型

$ \begin{array}{l} \lambda \left( s \right) = {s^{2 + m}} + {\beta _{i1}}{s^{2 + m - 1}} + \cdots + {\beta _{i\left( {2 + m - 1} \right)}}s + {\beta _{i\left( {2 + m} \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;{\left( {s + {\omega _0}} \right)^{2 + m}}, \end{array} $

由此可以得到所有的增益系数.

假设状态估计是理想的，即${\hat x_{i1}}$=θ_i、${\hat x_{i2}}={\dot \theta }_i$、${\hat x_{i3}}$=f_i(·)，可得

$ {{\ddot e}_{{\rm{p}}i}} + {k_{{\rm{d}}i}}{{\dot e}_{{\rm{p}}i}} + {k_{{\rm{p}}i}}{e_{{\rm{p}}i}} = 0. $

式中, e_pi=θ_di－θ_i.因此，设计k_pi和k_di, 使上述系统稳定且有期望的响应.

期望角速度和角加速度可以采用TD滤波器给出; 为了改善系统性能，误差项(${{{\hat{\dot{\theta }}}}_{\text{d}i}}-{{{\hat{x}}}_{i2}}$)和(${\theta _{{\rm{d}}i}} -{{\hat x}_{i1}}$)采用非线性函数fal(x, α, δ)取代

$ \begin{array}{l} fal\left( {x,\alpha ,\delta } \right) = \\ \left\{ \begin{array}{l} {\left| x \right|^\alpha }{\rm{sign}}\left( x \right),\;\;\;\;\left| x \right| > \delta ;\\ \frac{x}{{{\delta ^{1 - \alpha }}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\left| x \right| \le \delta ; \end{array} \right.,\delta > 0,0 < \alpha < 1. \end{array} $

得到控制器为

$ \begin{align} & {{u}_{i}}=\left( {{{\hat{\ddot{\theta }}}}_{\rm{d}i}}-{{{\hat{x}}}_{i3}} \right)+{{k}_{\rm{d}i}}fal\left( {{{\hat{\dot{\theta }}}}_{\rm{d}i}}-{{{\hat{x}}}_{i2}},{{\alpha }_{\rm{d}i}},{{\delta }_{\rm{d}i}} \right)+ \\ & \ \ \ \ \ \ \ {{k}_{\rm{p}i}}fal\left( {{\theta }_{\rm{d}i}}-{{{\hat{x}}}_{i1}},{{\alpha }_{\rm{p}i}},{{\delta }_{\rm{p}i}} \right). \\ \end{align} $

根据式(7)，同时考虑到末端负载的不确定性，m_n采用估计值替代，对应的质量矩阵记作${{\boldsymbol{\hat M}}_{\theta \theta, {\rm{s}}}}$，因此，慢时标子系统的控制输入为

$ {{\mathit{\boldsymbol{ }}\!\!\tau\!\!\rm{ }}_{\rm{s}}}={{{\mathit{\boldsymbol{\hat{M}}}}}_{\theta \theta ,\rm{s}}}\mathit{\boldsymbol{u}}. $

2.3 内环LQR控制器

将快时标子系统表达为状态空间的形式为

$ {{{\mathit{\boldsymbol{\dot{x}}}}}_{\rm{f}}}={{\mathit{\boldsymbol{A}}}_{\rm{f}}}{{\mathit{\boldsymbol{x}}}_{\rm{f}}}+{{\mathit{\boldsymbol{B}}}_{\rm{f}}}{{\mathit{\boldsymbol{u}}}_{\rm{f}}}. $

其中

$ {\mathit{\boldsymbol{A}}_{\rm{f}}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&\mathit{\boldsymbol{I}}\\ { - {\mathit{\boldsymbol{N}}_{qq}}\mathit{\boldsymbol{\tilde K}}}&{\bf{0}} \end{array}} \right],{\mathit{\boldsymbol{B}}_{\rm{f}}} = \left[ {\begin{array}{*{20}{c}} 0\\ {\mathit{\boldsymbol{N}}_{\theta q}^{\rm{T}}} \end{array}} \right],{\mathit{\boldsymbol{x}}_{\rm{f}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_{\rm{f}}}}\\ {\frac{{{\rm{d}}{\mathit{\boldsymbol{z}}_{\rm{f}}}}}{{{\rm{d}}\sigma }}} \end{array}} \right]. $

采用最优控制技术进行振动抑制，目标函数选择为

$ J = \frac{1}{2}\int_0^\infty {\left[ {\mathit{\boldsymbol{x}}_{\rm{f}}^{\rm{T}}{\mathit{\boldsymbol{Q}}_{\rm{f}}}{\mathit{\boldsymbol{x}}_{\rm{f}}} + \mathit{\boldsymbol{\tau }}_{\rm{f}}^{\rm{T}}{\mathit{\boldsymbol{R}}_{\rm{f}}}{\mathit{\boldsymbol{\tau }}_{\rm{f}}}} \right]{\rm{d}}t} . $

式中Q_f和R_f为权重系数矩阵.采用标准的LQR设计，快时标系统的控制输出为

$ {\mathit{\boldsymbol{\tau }}_{\rm{f}}} = - {\mathit{\boldsymbol{K}}_{\rm{f}}}{\mathit{\boldsymbol{x}}_{\rm{f}}} + {\mathit{\boldsymbol{K}}_{\rm{f}}}\left[ {\begin{array}{*{20}{c}} {{z_{\rm{s}}}}\\ {\bf{0}} \end{array}} \right]. $

其中:

$ \mathit{\boldsymbol{K = }} - \mathit{\boldsymbol{R}}_{\rm{f}}^{ - 1}\mathit{\boldsymbol{B}}_{\rm{f}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{f}}}\left( t \right). $

P_f通过求解Riccati方程获得:

$ {{\mathit{\boldsymbol{\dot P}}}_{\rm{f}}}\left( t \right) = - {\mathit{\boldsymbol{P}}_{\rm{f}}}\left( t \right){\mathit{\boldsymbol{A}}_{\rm{f}}} - \mathit{\boldsymbol{A}}_{\rm{f}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{f}}}\left( t \right) + {\mathit{\boldsymbol{P}}_{\rm{f}}}\left( t \right){\mathit{\boldsymbol{B}}_{\rm{f}}}\mathit{\boldsymbol{R}}_{\rm{f}}^{ - 1}\mathit{\boldsymbol{B}}_{\rm{f}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{\rm{f}}}\left( t \right) - {\mathit{\boldsymbol{Q}}_{\rm{f}}}. $

3 仿真研究 3.1 仿真参数

在仿真算例中，考虑具有两节柔性臂杆的机械臂，每节臂杆考虑两阶模态，相应的参数见表 1.仿真采用Simulink，通过四阶Runge-Kutta法求解，仿真步长0.000 5 s.

表 1 仿真参数 Table 1 Simulation parameters

机械臂的操作空间为{(θ₁, θ₂)|θ₁∈[0, 2π], θ₂∈[0, 2π]}，摄动参数计算为μ=0.016 7 s，系统的最小自然频率为59.8 rad/s，通过将所有的极点配置在－2.5，得到反馈增益为k_di=5.00和k_pi=6.25.因此，慢时标系统的带宽为6.2 rad/s，慢时标和快时标系统的分解是合理的. ESO估计器的极点配置在ω₀=20 rad/s，使其足够快，此时估计器增益为β₁=3ω₀, β₂=3ω₀², β₃=ω₀³. TD的参数设置为r₁₁=r₁₂=3 000, h₁₁₀=h₁₂₀=0.04, r₂₁=1 500, h₂₁₀=0.03, r₂₂=2 000, h₂₂₀=0.04. NPD的参数设置为α_p1=0.3, α_d1=0.5, δ_p1=0.2, δ_d1=0.7, α_p2=0.2, α_d2=0.4, δ_p2=0.2和δ_d2=0.9. LQR的权系数矩阵选择为

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_{\rm{f}}} = {\rm{diag}}\left( {100,10,10,10,10,10,10,10} \right),}\\ {{\mathit{\boldsymbol{R}}_{\rm{f}}} = {\rm{diag}}\left( {100,10} \right).} \end{array} $

机械臂的运动轨迹设计为

$ {\theta _i} = \left\{ \begin{array}{l} \frac{{{a_i}}}{2}\left[ {\sin \left( {{\omega _i}t - \frac{{\rm{ \mathsf{ π} }}}{2}} \right) + 1} \right],\;\;\;\;\;\;{\omega _i}t \le {\rm{ \mathsf{ π} ;}}\\ {a_i},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _i}t > {\rm{ \mathsf{ π} ;}} \end{array} \right.i = 1,2. $

其中a_i和ω_i为期望的最终角位置和转动速度.

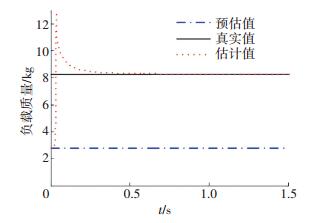
3.2 末端负载的估计性能

RLS参数设置为P₀=2 000和m_p0=m₂，其中m₂是预估负载质量.真实的负载质量为8.25 kg，因此，负载的不确定量为ΔM_p=2m₂=5.5 kg.末端负载估计器的性能如图 3所示.

图 3 对末端负载的估计性能 Figure 3 Estimation of mass of the unknown payload

其中黑色实线表示真实的负载质量，蓝色点划线表示预估负载质量，红色点线为负载估计器估计得到的负载质量.从图 3中可以看出，负载估计器以预估负载质量作为估计初值，当负载不确定量较大时，初始误差比较大，但估计值会向负载真值方向迅速变化，出现短暂的超调，并快速收敛到真值，收敛到5%误差的时间＜0.2 s.出现较大超调的主要原因是：运动初始阶段，关节转动的角度和角速度、臂杆振动的模态坐标值都很小，Φ≈0，对负载质量的估计近似奇异，误差较大.通常，为了避免激起臂杆的振动，机械臂操纵负载机动的过程很缓慢，因此，可以认为负载估计收敛速度足够快.

3.3 小末端负载不确定时的性能

当末端负载的不确定性比较小时，如ΔM_p=0.2m₂=0.55 kg，系统的响应如图 4所示.其中，设计轨迹参数为ω₁=ω₂=1 rad/s、a₁=π/3 rad/s、a₂=π/4 rad.为了方便，AADRC和ADRC分别表示ADRC控制器中采用和没采用RSL算法估计负载质量并进行补偿.作为对比，仿真中同时给出文献[15]中的计算力矩控制器(Computed torque controller, CTC)的响应.从图 4中可以看出，如果负载的不确定性比较小，AADRC和ADRC的性能基本一致.这主要是由于ADRC控制器本身就有一定的干扰抑制能力.采用CTC时，θ₁和θ₂都出现了明显的超调，且稳定时间较长.

图 4 角度跟踪响应(ω₁=ω₂=1 rad/s，ΔM_p=0.55 kg) Figure 4 Tracking performance (ω₁=ω₂=1 rad/s, ΔM_p=0.55 kg)

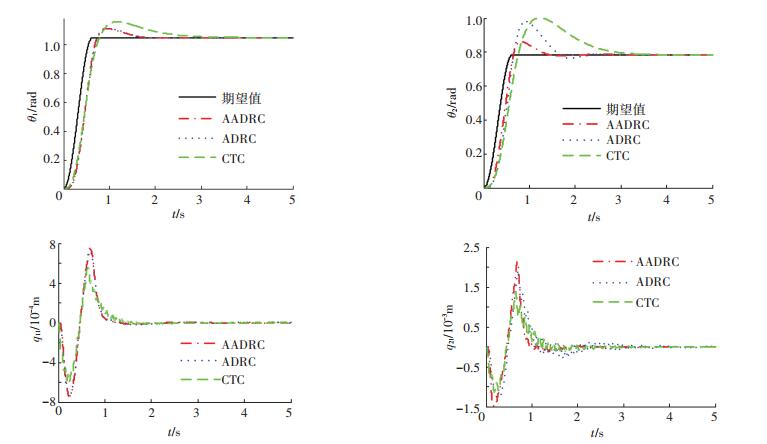
当机械臂的运动速度增加时，如ω₁=ω₂=5 rad/s，第1节连杆的响应基本一致，而第2节连杆的响应却明显不同.从图 5中可以看到，采用ADRC时，θ₂的超调量大于采用AADRC的，振动衰减的速度也比较慢.进一步比较图 4和图 5，机械臂运动速度的增加也导致了角度的超调量的增加.采用CTC时，θ₁和θ₂的超调也随着角速度增加而增加.

图 5 角度跟踪响应(ω₁=ω₂=5 rad/s，ΔM_p=0.55 kg) Figure 5 Tracking performance (ω₁=ω₂=5 rad/s, ΔM_p=0.55 kg)

3.4 大末端负载不确定时的性能

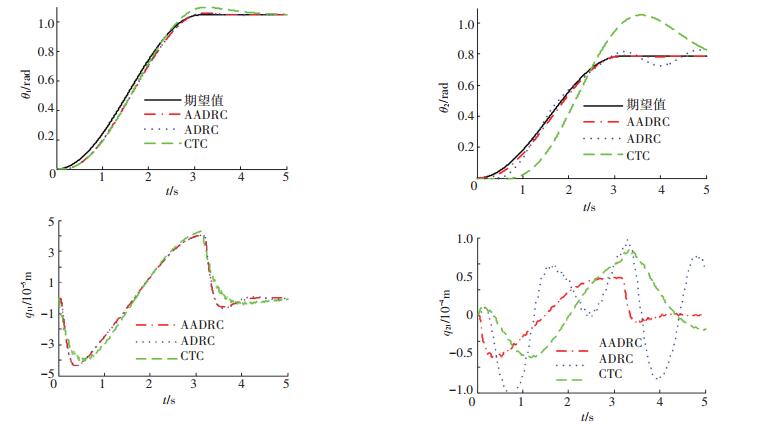
当末端负载不确定量增加时，如ΔM_p=5.5 kg，系统的响应如图 6所示.即使是在机械臂低速运动时(ω₁=ω₂=1 rad/s)，第2节臂杆的响应也明显不同.在对末端负载进行估计和补偿后，θ₂迅速趋于稳定.如果只采用ADRC，则θ₂存在明显的振荡.但是，末端负载不确定性的增加对第1节臂杆的影响很小.负载不确定性的增加也导致CTC的性能恶化，特别是θ₂，超调量达到了30%.

图 6 角度跟踪响应(ω₁=ω₂=1 rad/s，ΔM_p=5.5 kg) Figure 6 Tracking performance (ω₁=ω₂=1 rad/s, ΔM_p=5.5 kg)

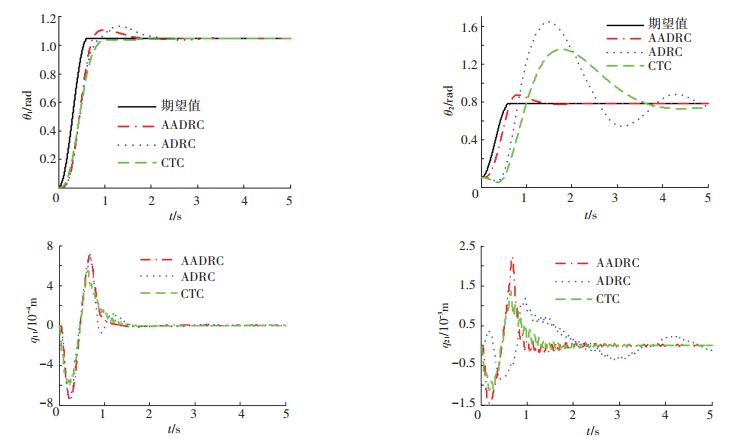
如果机械臂的运动速度增加，单独采用ADRC的响应性能更加恶化，如图 7所示.比较图 6和图 7，采用ADRC控制，在负载不确定增加时，随着机械臂运动速度的增加，θ₁的响应也明显的不同.如果负载质量不确定性得到补偿，机械臂速度增加对系统性能没有明显影响.采用CTC时，θ₂的响应性能也进一步恶化，然而θ₁并没有出现超调，但相比于其他两个控制器，有一定的滞后，这说明在这样的参数下，关节1的控制器构成了欠阻尼系统.

图 7 角度跟踪响应(ω₁=ω₂=5 rad/s，ΔM_p=5.5kg) Figure 7 Tracking performance (ω₁=ω₂=5 rad/s, ΔM_p=5.5 kg)

3.5 不同速度下系统响应分析

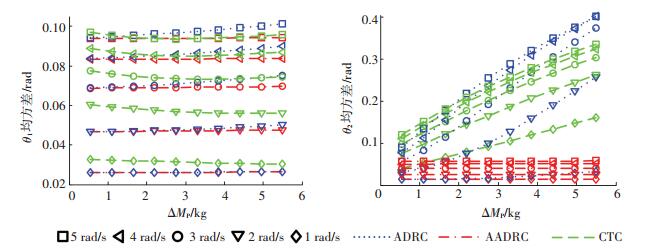
在不同速度下，系统响应随着负载不确定性的变化见图 8.其中，ω=ω₁=ω₂∈[1, 2, 3, 4, 5] rad/s，ΔM_p=0.2 kg, k=1, 2, …, 10.均方差(mean square error)定义为

图 8 不同速度下的跟踪响应 Figure 8 Summary of tracking performance at different maneuver speeds

$ {\rm{MSE}}\left( x \right) = \sqrt {\frac{1}{{{t_{\rm{f}}}}}\int_0^{{t_{\rm{f}}}} {{{\left( {{x_d} - x} \right)}^2}{\rm{d}}t} } = \sqrt {\frac{1}{N}\sum\limits_N {{{\left( {{x_d} - x} \right)}^2}} } , $

其中，t_f是仿真时长，N是采样数量.从图中可以看出，无论采用AADRC、ADRC，还是CTC，θ₁和θ₂的均方差都随ω增加而增加.这主要是由于随着运动速度的增加，超调量也增加.采用ADRC，θ₁的均方差随着负载不确定性的增加并不明显，θ₂的均方差变化显著，特别是运动速度较大时.采用CTC时，在负载质量不确定度较小时，θ₁的均方差比采用ADCRC和AADRC时大，但随着负载不确定性的增加而减小，在负载不确定性较大时，其性能优于ARDC，但不如AADRC; θ₂的均方差随着负载不确定性的增加迅速增加，增速比ADRC略缓.总体看来，在负载质量得到估计和补偿，即采用AADRC时，系统响应对负载的变化和速度变化具有鲁棒性.

4 结论

1) 针对多柔性臂杆机械臂的控制问题，本文提出了一种新的控制器结构.首先采用奇异摄动理论将系统分解为快时标和慢时标两个子系统.慢时标子系统采用自适应自抗扰控制，快时标子系统采用线性二次型控制器.

2) 自适应自抗扰控制器采用微分跟踪器获得期望角度的角速度和角加速度，采用状态扩张估计器获得估计真实的角速度和角加速度及干扰，采用迭代最小二乘算法估计负载的不确定性，采用非线性比例微分控制器保证系统的鲁棒性.

3) 仿真结果表明，无论采用AADRC，还是采用ADRC，末端负载的不确定性对臂杆振动和关节转动的控制精度的影响随关节转动速度的增加而变得更加明显.关节2的转动角度控制精度和臂杆2的振动受末端负载的不确定性的影响比关节1和臂杆1更为明显.

4) 采用迭代最小二乘算法估计负载的不确定性并进行补偿后，AADRC相比于ADRC，对末端负载不确定性的变化和关节转动速度的变化都具有更好的鲁棒性.

参考文献

[1]	贺亮, 王有峰, 吴蕊, 等. 空间机器人多臂精准协同控制技术[J]. 哈尔滨工业大学学报, 2013, 45(9): 107-112. HE Liang, WANG Youfeng, WU Rui, et al. Precision synergy control technology for multi-arm space robots[J]. Journal of Harbin Institute of Technology, 2013, 45(9): 107-112. DOI: 10.11918/j.issn.0367-6234.2013.09.019
[2]	居鹤华, 冷舒. 利用虚拟传感器的巡视器机械臂碰撞检测算法[J]. 哈尔滨工业大学学报, 2016, 48(1): 58-65. JV Hehua, LENG Shu. A collide detection algorithm based on virtual sensors of lunar rover manipulator[J]. Journal of Harbin Institute of Technology, 2016, 48(1): 58-65. DOI: 10.11918/j.issn.0367-6234.2016.01.009
[3]	CORNELIA A, JOHN D, THOMAS C J. Flexible multi-body dynamic modeling of a Tendon-Actuated Lightweight In-Space MANipulator (TALISMAN)[C]// AIAA SPACE 2015 Conference and Exposition. Pasadena: AIAA Press, 2015: AIAA 2015-4629. DOI: 10.2514/6.2015-4629.
[4]	JARZEBOWSKA E, PIETRAK K. Constrained mechanical systems modeling and control: a free-floating space manipulator case as a multi-constrained system[J]. Robotics & Autonomous Systems, 2014, 62(10): 1353-1360. DOI: 10.1016/j.robot.2014.04.004
[5]	刘伊威, 王滨, 姚郁, 等. 乒乓球机器人手臂及其击球策略[J]. 哈尔滨工业大学学报, 2013, 45(3): 33-38. LIU Yiwei, WANG Bin, YAO Yu, et al. Dexterous robot arm for table tennis and hitting strategy[J]. Journal of Harbin Institute of Technology, 2013, 45(3): 33-38. DOI: 10.11918/j.issn.0367-6234.2013.03.006
[6]	闫继宏, 郭鑫, 刘玉斌, 等. 一种模块化机械臂的设计与运动学分析[J]. 哈尔滨工业大学学报, 2015, 47(1): 20-25. YAN Jihong, GUO Xin, LIU Yubin, et al. The design and kinematic analysis of a modular manipulator[J]. Journal of Harbin Institute of Technology, 2015, 47(1): 20-25. DOI: 10.11918/j.issn.0367-6234.2015.01.004
[7]	TSO S, YANG T, XU W, et al. Vibration control for a flexible-link robot arm with deflection feedback[J]. International Journal of Non-Linear Mechanics, 2003, 38(1): 51-62. DOI: 10.1016/S0020-7462(01)00040-3
[8]	PEREIRA E, APHALE S S, FELIU V, et al. Integral resonant control for vibration damping and precise tip-positioning of a single-link flexible manipulator[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(2): 232-240. DOI: 10.1109/TMECH.2009.2039713
[9]	MORALES R, FELIU V, JARAMILLO V. Position control of very lightweight single-link flexible arms with large payload variations by using disturbance observers[J]. Robotics and Autonomous Systems, 2012, 60(4): 532-547. DOI: 10.1016/j.robot.2011.11.016
[10]	SHARMA K S, SUTTON R, TOKHI O M. Local model and controller network design for a single-link flexible manipulator[J]. Journal of Intelligent & Robotic Systems, 2014, 74(3/4): 605-623. DOI: 10.1007/s10846-013-9847-1
[11]	VAKIL M, FOTOUHI R, NIKIFORUK P. Causal end-effector inversion of a flexible link manipulator[J]. Mechatronics, 2009, 19(7): 1197-1210. DOI: 10.1016/j.mechatronics.2009.03.010
[12]	PAYO I, FELIU V, CORTAZAR D O. Force control of a very lightweight single-link flexible arm based on coupling torque feedback[J]. Mechatronics, 2009, 19(3): 334-347. DOI: 10.1016/j.mechatronics.2008.10.003
[13]	GURSES K, BUCKHAM B J, PARK E J. Vibration control of a single-link flexible manipulator using an array of fiber optic curvature sensors and PZT actuators[J]. Mechatronics, 2009, 19(2): 167-177. DOI: 10.1016/j.mechatronics.2008.09.005
[14]	PARK H W, YANG H S, PARK Y P, et al. Position and vibration control of a flexible robot manipulator using hybrid controller[J]. Robotics and Autonomous Systems, 1999, 28(1): 31-41. DOI: 10.1016/S0921-8890(99)00027-5
[15]	SUBUDHI B, MORRIS A S. Singular perturbation approach to tra-jectory tracking of flexible robot with joint elasticity[J]. International Journal of Systems Science, 2003, 34(3): 167-179. DOI: 10.1080/0020772031000135450
[16]	KHORASANI K. Adaptive control of flexible-joint robots[J]. IEEE Transactions on Robotics and Automation, 1992, 8(2): 250-267. DOI: 10.1109/70.134278
[17]	SPONG M, KHORASANI K, KOKOTOVIC P. An integral manifold approach to the feedback control of flexible joint robots[J]. IEEE Journal of Robotics and Automation, 1987, 3(4): 291-300. DOI: 10.1109/JRA.1987.1087102
[18]	GHORBEL F, SPONG M. Integral manifolds of singularly perturbed systems with application to rigid-link flexible-joint multibody systems[J]. International Journal of Non-Linear Mechanics, 2000, 35(1): 133-155. DOI: 10.1016/S0020-7462(98)00092-4
[19]	VAKIL M, FOTOUHI R, NIKIFORUK P. Maneuver control of the multilink flexible manipulators[J]. International Journal of Non-Linear Mechanics, 2009, 44(8): 831-844. DOI: 10.1016/j.ijnonlinmec.2009.05.008
[20]	SICILIANO B, PRASAD J, CALISE A. Output feedback two-time scale control of multilink flexible arms[J]. Journal of Dynamic Systems, Measurement, and Control, 1992, 114(1): 70-77. DOI: 10.1115/1.2896509
[21]	SUBUDHI B, MORRIS A. Dynamic modelling, simulation and control of a manipulator with flexible links and joints[J]. Robotics and Autonomous Systems, 2002, 41(4): 257-270. DOI: 10.1016/S0921-8890(02)00295-6
[22]	PRZYBYLA M, KORDASZ M, MADONSKI R, et al. Active disturbance rejection control of a 2d of manipulator with significant modeling uncertainty[J]. Bulletin of the Polish Academy of Sciences Technical Sciences, 2012, 60(3): 509-520. DOI: 10.2478/v10175-012-0064-z
[23]	BECEDAS J, TRAPERO J, FELIU V, et al. Adaptive controller for single-link flexible manipulators based on algebraic identification and generalized proportional integral control[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2009, 39(3): 735-751. DOI: 10.1109/TSMCB.2008.2008905
[24]	CHU Zhongyi, CUI Jing, SUN Fuchun. Fuzzy adaptive distur-bance-observer-based robust tracking control of electrically driven free-floating space manipulator[J]. IEEE Systems Journal, 2014, 8(2): 343-352. DOI: 10.1109/JSYST.2012.2220171
[25]	CAI Guoping, LIM C. Optimal tracking control of a flexible hub-beam system with time delay[J]. Multibody System Dynamics, 2006, 16(4): 331-350. DOI: 10.1007/s11044-006-9029-z
[26]	DWIVEDY S, EBERHARD P. Dynamic analysis of flexible manipulators, a literature review[J]. Mechanism and Machine Theory, 2006, 41(7): 749-777. DOI: 10.1016/j.mechmachtheory.2006.01.014