2. 哈尔滨工业大学 机电工程学院,哈尔滨 150001;
3. 浙江大学 机械工程学院,杭州 310027
2. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China;
3. College of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China
高温合金是一种沉淀强化型镍基铸造高温合金,具有强度高、抗疲劳性强、高温下热稳定等特性,因此被广泛应用于航天航空领域的热端部件[1].但是,由于高温合金含有金属互化物、碳化物、氮化物和硬点等强化相,是一种典型的难加工材料,尤其是此类材料微孔(≤50 μm)的加工,目前的主要加工方法有电火花加工、电解加工、复合加工方法等[2],但还存在加工精度不高、效率低下等问题.飞秒激光加工以其极窄的脉宽和极高的峰值功率密度等优点,可以有效地限制加工过程中的热扩散,消除重铸层、热影响区和熔渣等加工表面缺陷[3-4],在高温合金微孔加工领域具有广阔的应用前景[5].
众多学者对飞秒激光与金属的作用过程,从理论上和试验角度进行了大量研究.在理论分析方面,由于飞秒激光与物质作用过程中,电子和晶格的温度变化并不平衡,因此传统的傅里叶热传导定律并不适用.双温模型(two-temperature model)最初是Anisimov等[6]根据玻尔兹曼输运方程(Boltzmann transport equation)推导得出,用来描述超短脉冲激光与物质作用过程中的电子和晶格之间的热传递过程. Karim等[7]基于连续二维双温模型结合混合计算模型、经典分子动力学模型,对飞秒激光与纯铬靶的相互作用过程进行了数值仿真,揭示了铬靶在飞秒激光作用下的熔化、再凝固、相爆炸、液滴和熔融金属喷出等微变过程. Povarnitsyn等[8]采用二维双温流体力学和分子动力学模型对飞秒激光加工纯铝靶材过程中的熔融和破碎现象进行仿真研究,结果表明当激光能量密度在0.1~20 J/cm2时,两种模型均能与实验结果很好吻合.流体力学模型可以定量地描述激光与材料作用过程中的相变;分子动力学模型计算较慢,但是能准确地重现原子层面上的过程,例如破碎液相中的成核现象等.对比一些学者的研究发现,在激光与金属的作用过程中,加工区域沿光轴轴向的温度梯度较大,而沿光斑径向的温度梯度几乎可以忽略.因此采用简化的一维双温模型可以较为准确高效地反映飞秒激光与金属材料作用过程中的温度变化. Zhang等[9]通过在激光光源项中增加脉冲延迟,改进了一维连续双温模型,利用有限差分法分析了三脉冲飞秒激光与Ni-Ti合金的作用过程,研究发现,相比于单脉冲激光加工,三脉冲激光加工引起的脉冲累积效应可以有效降低材料的去除阈值,从而提升激光蚀除效率.但是仿真应用Ni-Ti合金的重要参数并没有经过推导,而是直接采用单晶镍的相关参数. Ma等[10]观察到应用0.1~160 J/cm2能量密度的飞秒激光烧蚀镍基CMSX-4高温合金过程中存在两种材料去除机制:当能量密度在去除阈值18倍的范围内(0.3~5.3 J/cm2),蚀除速率主要和光学吸收深度有关,能量密度在此范围内时, 加工过程中不会出现熔融等现象;当能量密度>去除阈值的18倍(>5.3 J/cm2)时,蚀除速率和激光功率密度成对数关系,此时热累积现象会比较显著,加工过程中存在一定的重铸层. Das等[11]利用飞秒激光在具有陶瓷涂层的CMSX-4高温合金表面加工出直径为300、600 μm,深度为1.5 mm的微孔,研究发现,通过螺旋进给激光焦点的方式可以有效地降低孔的锥度,但是扫描次数过多会引起热累积效应,在孔的出入口存在显著的热影响区以及微裂纹.
以往对飞秒激光加工金属的理论研究及仿真过程中,应用的材料大多是纯金属,对于合金的物理参数推导缺少详细的过程,同时理论模型的准确性缺少相应的试验验证.本文基于普朗克方程和固体物理学中的线性假设理论,推导出K24高温合金的一系列关键的光学物理参数.结合一维双温方程和有限差分法,仿真出飞秒激光作用过程中电子和晶格的温度变化.通过初步试验验证了数值模型的精度.进行了紫外飞秒激光加工K24高温合金的正交试验,结合极差分析和详细的理论分析,得出不同加工参数对微孔精度和质量的影响规律.
1 理论基础 1.1 一维双温模型的解析考虑到加工过程中飞秒激光的能量主要沿着激光光轴方向传导,沿光斑径向方向的传热几乎可以忽略不计,因此简化双温模型为一维模式:
| $ {C_{\rm{e}}}\frac{{\partial {T_{\rm{e}}}}}{{\partial t}} = - \frac{\partial }{{\partial z}}\left( {{k_{\rm{e}}}\frac{{\partial {T_{\rm{e}}}}}{{\partial z}}} \right) - g\left( {{T_{\rm{e}}} - {T_{\rm{i}}}} \right) + I\left( {t,z} \right), $ | (1) |
| $ {C_i}\frac{{\partial {T_{\rm{i}}}}}{{\partial t}} = g\left( {{T_{\rm{e}}} - {T_{\rm{i}}}} \right), $ | (2) |
| $ I\left( {t,z} \right) = {I_0}\left( {1 - R} \right)\alpha \left( {t,z} \right)\exp \left( { - \int_0^z {\alpha \left( {t,z} \right)\left. {{\rm{d}}z} \right)} } \right). $ |
式中:I(t, z)为高斯分布的光源项;Ce为电子热容, Ce=γCe(Te);Ci为晶格热容;ke为电子热导率,ke(Te)=(1/3)ve2(Te)τe(Te)Ce(Te);τe为自由电子弛豫时间;ve为电子速度;ki为晶格热导率;Te和Ti分别为电子和晶格温度;g为电声耦合系数, g=π2mene(t, r, z)cs2/(6τ(Te)Te(t, r, z)).本文中镍基合金的电声耦合系数g采用的是Wellershoff等[12]提出的3.647×1017 W·m-3k-1.
对双温模型按空间域和时域进行网格划分,通过有限差分法进行求解.利用隐式迭代法对式(1) 和(2) 进行解析.实际加工过程中,飞秒激光对靶材的蚀除在室温环境下进行.为保持与实际加工条件一致,初始温度和边界温度均设置为300 K.
1.2 K24高温合金关键参数的确立 1.2.1 K24高温合金吸收系数与反射率在飞秒激光与金属作用过程中,加工区域会产生大量的自由电子.自由电子密度的变化会引起材料自身一些光学属性的变化,例如材料的吸收系数与反射率.确立光源项时,需要确立特定激光参数下K24高温合金的一系列光学参数,从而提高双温模型求解过程的准确性.
基于Fokker-Planck方程,得出在高斯型激光作用下,加工区域自由电子密度在时空中的变化为[13]
| $ \partial {n_{\rm{e}}}\left( {t,r,z} \right)/\partial t = \beta \left( I \right){n_{\rm{e}}}\left( {t,r,z} \right) + P\left( I \right). $ | (3) |
式中:ne(t, r, z)为自由电子密度;r为距离高斯光束光轴中心的距离;z为距离靶材表面的深度;I为激光强度;β(I)为碰撞电离项,β(I)=αiI(t, r, z);αi为碰撞吸收系数;P(I)为多光子电离项,P(I)=δN(I(t, r, z))N;δN为多光子吸收系数.根据Goya等[14]的研究,从材料反射的高斯光束依旧遵循高斯分布.因此,材料内激光强度可表示为
| $ \begin{array}{l} I\left( {t,r,z} \right) = \sqrt {\beta /{\rm{\pi }}} \left( {F/{t_{\rm{p}}}} \right)\left( {1 - R\left( {t,r} \right)} \right)\alpha \left( {t,r,z} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - \frac{{{r^2}}}{{r_0^2}} - \beta {{\left( {\frac{t}{{{t_{\rm{p}}}}}} \right)}^2} - \int\limits_0^z {\alpha \left( {t,r,z} \right){\rm{d}}z} } \right). \end{array} $ | (4) |
式中:R(t, r)为z=0时的材料反射率;r0为激光光斑半径;tp为激光脉宽;I0为激光峰值功率密度,I0=
K24高温合金的光学特性,例如反射率与吸收系数是由其介电函数决定的.自由电子的介电函数可表示为[15-16]
| $ \varepsilon \left( {t,r,z} \right) = 1 + \left( {\frac{{{n_{\rm{e}}}\left( {t,r,z} \right){e^2}}}{{{m_{\rm{e}}}{\varepsilon _0}}}} \right)\left( {\frac{{ - \tau _{\rm{e}}^2\left( {t,r,z} \right) + {\rm{i}}/\omega }}{{1 + {\omega ^2}\tau _{\rm{e}}^2\left( {t,r,z} \right)}}} \right). $ | (5) |
式中:
在临界密度时,等离子频率ncr与激光频率相同,
| $ {n_{{\rm{cr}}}} = 4{{\rm{\pi }}^2}{c^2}{m_{\rm{e}}}{\varepsilon _0}/\left( {{\lambda ^2}{{\rm{e}}^2}} \right). $ | (6) |
式中:c为真空中的光速;λ为激光波长.
复杂的介电函数可以用实部和虚部的表达式:
| $ \begin{array}{l} \varepsilon \left( {t,r,z} \right) = {\varepsilon _1}\left( {t,r,z} \right) + {\rm{i}}{\varepsilon _2}\left( {t,r,z} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 + \frac{{\omega _{\rm{p}}^2\left( {{n_{\rm{e}}}} \right)\tau _{\rm{e}}^2\left( {t,r,z} \right)}}{{1 + {\omega ^2}\tau _{\rm{e}}^2\left( {t,r,z} \right)}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{i}}\left( {\frac{{\omega _{\rm{p}}^2\left( {{n_{\rm{e}}}} \right){\tau _{\rm{e}}}\left( {t,r,z} \right)}}{{\omega \left( {1 + {\omega ^2}\tau _{\rm{e}}^2\left( {t,r,z} \right)} \right)}}} \right). \end{array} $ | (7) |
电离材料表面的反射率可以表示为
| $ R\left( {t,r} \right) = \frac{{{{\left( {{f_1}\left( {t,r,0} \right) - 1} \right)}^2} + f_2^2\left( {t,r,0} \right)}}{{{{\left( {{f_1}\left( {t,r,0} \right) + 1} \right)}^2} + f_2^2\left( {t,r,0} \right)}}. $ |
式中: f1为正常的折射系数,且
| $ {f_1}\left( {t,r,z} \right) = \sqrt {\left( {{\varepsilon _1}\left( {t,r,z} \right) + \sqrt {\varepsilon _1^2\left( {t,r,z} \right) + \varepsilon _2^2\left( {t,r,z} \right)} } \right)/2} ; $ |
f2为消光系数,
| $ {f_2}\left( {t,r,z} \right) = \sqrt {\left( { - {\varepsilon _1}\left( {t,r,z} \right) + \sqrt {\varepsilon _1^2\left( {t,r,z} \right) + \varepsilon _2^2\left( {t,r,z} \right)} } \right)/2} . $ |
通过自由电子加热,等离子体对吸光强度的吸收系数表达为
| $ {\alpha _h}\left( {t,r,z} \right) = 2\omega {f_2}\left( {t,r,z} \right)/c $ | (8) |
式(8) 的吸收系数只代表由自由电子加热引起的对激光能量的吸收系数.还有一部分能量是通过多光子电离进行吸收的.对于飞秒烧蚀金属材料,激光能量吸收包括自由电子热化和电离两种吸收,因此材料对激光的吸收系数为α(t, r, z)=αh(t, r, z)+ αine(t, r, z)U1,式中,U1是材料的逸出功,本文中取值为4.2 eV.
基于式(3)~(8),在Matlab的环境下对K24高温合金表面激光光束中心处的吸收系数和反射率变化曲线进行求解. r0、F、ω、tp的值分别取为10 μm、5 J/cm2、30 kHz和300 fs.求解结果见图 1.
|
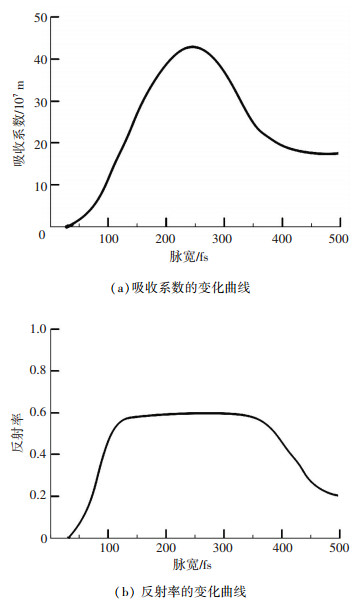
图 1 不同激光脉宽下光斑中心处K24高温合金吸收系数、反射率的变化曲线 Figure 1 Variation curve of absorption coefficient, reflectivity of K24 superalloy under different laser pulse width in the center of laser spot |
由图 1(b)可知,K24高温合金的的反射率在激光脉宽在 < 100 fs时会逐步上升,脉宽>400 fs时会逐步下降.飞秒激光加工区域会产生自由电子,相应的存在一个临界自由电子密度.当激光脉宽 < 100 fs时,自由电子密度增加;当产生的自由电子密度接近临界值时(脉宽大约为100 fs),材料反射率在极短的时间内升高;脉宽在100~400 fs范围内时,反射率基本稳定在0.55,在这个脉宽范围内,自由电子的产生主要是依赖于处于高能激发态的自由电子的碰撞电离,这个效应对靶材吸收系数的影响大于对反射率的影响;当脉宽>400 fs时,加工区域自由电子密度低于临界值,因此靶材反射率会下降.
由于仿真中激光脉宽选取300 fs,因此根据图 1(b)可得K24高温合金表面反射率约为0.55.
1.2.2 K24高温合金晶格热容和电子比热系数晶格热容和电子比热系数是K24高温合金的固有物理属性,与反射率和吸收系数不同,其数值不会受到激光强度变化的影响.在忽略固溶效应的前提下,K24高温合金的电子和晶格热容可假设为其主要组成元素的电子和晶格的线性叠加.利用XRD荧光光谱分析仪(AXIOS-PW4400) 检测本文中使用的K24高温合金的主要元素组成,结果见表 1:
| 表 1 K24高温合金内主要元素质量分数 Table 1 Mass fraction of main components in K24 superalloy |
基于描述晶格振动的德拜模型,纯金属的晶格热容可以写成[16]
| $ {C_{\rm{i}}} = qN{k_{\rm{B}}}{\left( {\frac{T}{{{\theta _{\rm{D}}}}}} \right)^3}\int\limits_0^{\frac{{{\theta _{\rm{D}}}}}{T}} {\frac{{{x^4}{{\rm{e}}^x}}}{{{{\left( {{{\rm{e}}^x} - 1} \right)}^2}}}} . $ | (9) |
式中:θD是德拜温度,根据Yu等[17]的计算可得,Ni、C、Cr、Al、Ti、Mo的德拜温度分别为450、2 230、630、408、420、570和380 K;N为单位摩尔质量内的总原子数;kB为玻尔兹曼常数.由于初始温度为300 K,式(9) 可以简化为式(10),即著名的德拜T3定律.
| $ {C_{\rm{i}}} = \left( {12{{\rm{\pi }}^4}/5} \right)N{k_{\rm{B}}}{\left( {T/{\theta _{\rm{D}}}} \right)^3}. $ | (10) |
K24高温合金的晶格热容可写为
| $ {C_{{\rm{iK24}}}} = a{C_{{\rm{iNi}}}} + b{C_{{\rm{iC}}}} + c{C_{{\rm{iCr}}}} + d{C_{{\rm{iAl}}}} + e{C_{{\rm{iTi}}}} + f{C_{{\rm{iMo}}}} + g{C_{{\rm{iCo}}}}. $ |
式中:a~g代表K24高温合金中元素的质量分布. CiK24的计算结果为2.442×106 J·m-3·k-1.
根据Lin等[18]的研究,电子热容Ce和温度具有线性关系:
| $ {C_{\rm{e}}} = \gamma {T_{\rm{e}}}. $ |
式中:γ为电子比热系数,γ=π2NkB/(2 TF);TF为费米温度,其值约为5×104 K.同样利用线性假设理论,γK24可以写为
| $ \begin{array}{l} {\gamma _{{\rm{K24}}}} = {\gamma _{{\rm{Ni}}}} + b{\gamma _{\rm{C}}} + c{\gamma _{{\rm{Cr}}}} + d{\gamma _{{\rm{Al}}}} + e{\gamma _{{\rm{Ti}}}} + \\ \;\;\;\;\;\;\;\;\;f{\gamma _{{\rm{Mo}}}} + g{\gamma _{{\rm{Co}}}}. \end{array} $ |
计算得γK24的值为63.5 J·m-3·k-2.
2 试验方法试验中使用的飞秒激光器是二极管抽运锁模Yb:KGW固体激光器(Pharos, Light Conversion),加工过程中使用的辅助气为氮气,输出激光波长为342 nm,脉宽300 fs,频率为30 kHz时的平均功率为1 W.聚焦后的激光光束直径2ω0计算公式为
| $ 2{\omega _0} = 4 \cdot \lambda \cdot f/\left( {\pi \cdot d} \right) \cdot {M^2}. $ |
式中:λ为激光波长,为342 nm;f是聚焦镜的焦距,为103 mm;d是经过扩束之后达到聚焦镜前端的激光光束直径,为4.8 mm;M2为TEM00模式下激光的光束质量.根据激光器的出厂报告,其值为1.07.因此,计算可得应用的聚焦激光光束直径约为10 μm.
本文采用了逐层扫描的打孔模式,即工件在厚度上被分为η层.激光光斑在同一层面上相对于工件移动相同的轨迹.本文中每层的轨迹是4个同心圆,半径分别是d1 (40 μm)、d2 (60 μm)、d3(80 μm)、d4(100 μm).在同一层面上,激光先扫描d4,然后逐个跳转至d3、d2、d1.扫描策略见图 2.当扫描完某一层面后,激光光斑会相对于工件向下进给至另一层面,继续进行相同轨迹的扫描.

|
图 2 飞秒激光逐层扫描策略示意 Figure 2 Schematic diagram of layer-by-layer laser scanning strategy |
基于1.1和1.2建立的理论模型,飞秒激光与K24高温合金作用之后,距离材料表面不同深度上电子和晶格的温度分布以及晶格的平衡温度见图 3.其中α代表距离工件表面的深度.
|
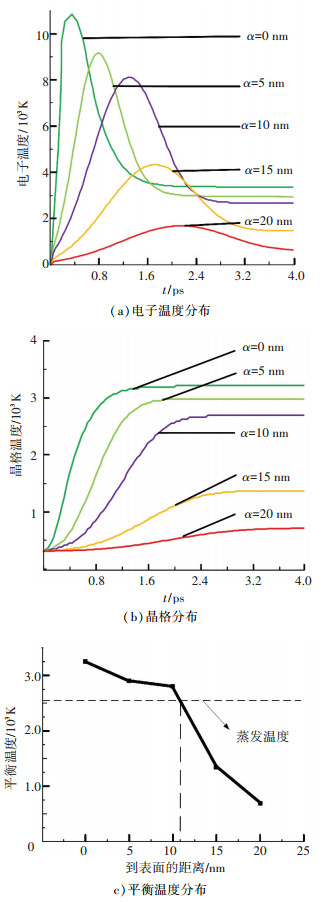
图 3 不同深度上电子温度、晶格温度、平衡温度的分布 Figure 3 Distribution of electron temperature, lattice temperature, equilibrium temperature in different depth from surface |
由图 3可以看出,不同深度上电子温度的变化规律基本一致.然而,峰值温度、达到平衡温度的时间以及平衡温度的值差异较大.同时可以发现,单脉冲飞秒激光加工时,激光能量主要沉积在靶材表面,只有很少一部能量能穿透到内部.根据Hilpert等[19]学者的研究,镍基高温合金的熔点大约为1 320 K,完全液化温度约为1 728 K,蒸发温度约为2 536 K.本文中把蒸发温度2, 536 K设定为材料从基体剥离的临界温度.当电子和晶格的平衡温度大于2 536 K时,材料可认为从基体剥离; 反之,如果电子和晶格的平衡温度低于2 536 K,那么加工区域材料就无法被蚀除.根据图 3(c)可知,电子和晶格的平衡温度变化曲线与蒸发温度线的交点对应的靶材深度z约为10.6 nm.因此,可以认为,脉宽为300 fs,频率为30 kHz,能量密度为5 J/cm2的342 nm飞秒激光对K24高温合金的单脉冲蚀除深度约为10.6 nm.
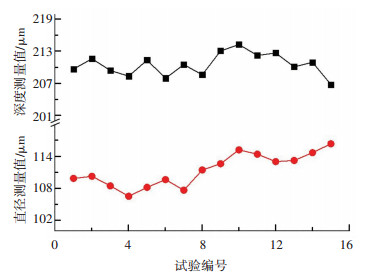
3.2 验证试验结果分析为验证建立模型和仿真结果的准确性,保持激光参数与仿真参数不变,进行了验证试验.试验参数见表 2.加工出的典型微坑剖面图见图 4.试验结果见图 5.计算后可知,微坑平均深度约为210.54 μm,入口平均直径约为111.45 μm.

|
图 4 典型微坑的剖面形貌 Figure 4 Typical profile morphology of micro dimple |
|
图 5 验证试验结果 Figure 5 Measuring results of verification experiments |
| 表 2 验证试验的加工参数 Table 2 Processing parameters of verification experiments |
总激光脉冲数为
| $ N = {\rm{\pi }}\left( {{d_1} + {d_2} + {d_3} + {d_4}} \right)/v \cdot f \cdot l. $ | (11) |
代入表 2中的参数,计算可得N为2 637 600.由图 4可知,微坑剖面可近似为圆锥形.因此可以认为单脉冲激光蚀除体积为
| $ {V_1} = \left( {{\rm{\pi }}{d^2}h/\left( {3N} \right.} \right). $ | (12) |
单脉冲蚀除深度设为z,则单脉冲蚀除体积又可写为
| $ {V_1} = {\rm{\pi }}{r^2}z/3. $ | (13) |
结合式(11)~(13) 可得z约为9.90 nm.对比仿真结果和试验结果,发现两者之间存在0.7 nm的误差.可以从以下两个角度去分析这个误差产生的原因.第一,在仿真过程中,计算K24高温合金的电子热容和晶格热容时,忽略了固溶效应,而该效应会给线性叠加假设带来一定误差,同时,微坑的体积也不完全是标准的圆锥体;第二,飞秒激光和K24高温合金作用过程中,会在加工区域产生大量等离子体, 这些等离子体会吸收激光能量,同时引起激光束的折射,进而影响后续激光脉冲的加工效率; 此外,相比单脉冲激光加工,多脉冲激光加工时会存在脉冲累积效应, 该效应会降低加工区域材料的去除阈值,也会对激光加工效率带来一定影响.考虑到以上的误差来源,分析认为,仿真结果与试验结果之间存在的误差是合理的.
3.3 正交试验结果分析为探究一系列加工参数对微孔形貌的影响规律,进行了四因素三水平紫外飞秒激光打孔正交试验,试验参数见表 3.此时激光脉宽设置为300 fs,频率设置为30 kHz.每组试验进行5次.加工出微孔的圆度标定采用IOS 1101标准的最小圆度法,见图 6.加工出微孔的轮廓可由一个最大的外圆C1和最小的内圆C2包围,两个圆的直径差即为圆度Δr. Δr越小,微孔的出口或者入口越圆整.加工出的微孔出入口直径的测量结果和圆度、锥度的计算结果见图 7, 不同加工参数对微孔出口圆度和锥度的效应曲线见图 8.

|
图 6 最小圆度法示意 Figure 6 Schematic diagram of least roundness method |

|
图 7 微孔出入口的直径、圆度和锥度的测量和计算结果 Figure 7 Measurement and calculation results of entrance and exit diameter, roundness and taper of micro holes |

|
图 8 不同加工参数对微孔出口圆度与锥度的效应曲线 Figure 8 Response curve of different processing parameters on exit roundness and taper of micro holes |
|
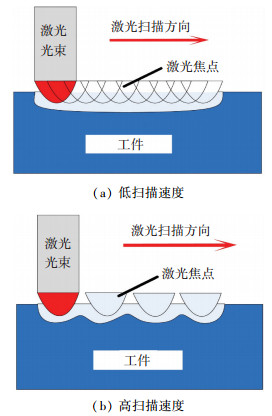
图 9 不同扫描速度对脉冲重叠度的影响 Figure 9 Effect of scanning velocity on overlap distribution of laser spot |
| 表 3 正交试验参数组合 Table 3 Parameter combinations of orthogonal experiments |
由图 8可知,较低的扫描速度、较小的进给距离、中等的扫描次数和较高的激光平均功率可以加工出精度更高,形状更加规则的微孔.在4个试验参数中,扫描速度对微孔出口圆度以及锥度影响最大,其次是进给距离、激光平均功率和扫描速度.
首先,激光的扫描速度直接影响激光焦点的重叠程度,示意图见9.随着扫描速度的减小,脉冲重叠度增大.本文中,较高脉冲重叠度的脉冲序列可近似认为是具有纳秒脉冲延迟的双脉冲序列.根据Yang等[20]学者的研究,相比于单脉冲飞秒激光加工,具有脉冲延迟的双脉冲飞秒激光加工时材料的去除阈值会减小,即所谓的脉冲累积效应.因此,较高的脉冲重叠度不仅可以增加单位面积内沉积的激光能量,也可以减小加工区域的材料去除阈值.进而提高每一个扫描层面上材料的蚀除效率,最终加工出锥度较小以及出口圆度较好的微孔.
其次,不同的进给距离代表着每次进给时飞秒激光的焦平面位移不同的步长.在焦平面上,飞秒激光的能量密度分布为
| $ F\left( x \right) = {F_0}{{\rm{e}}^{\frac{{ - 2{x^2}}}{{{w^2}}}}}. $ |
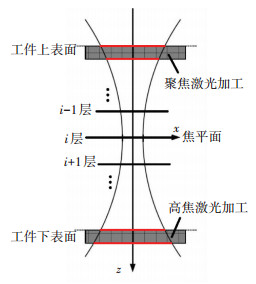
式中:w为激光光斑焦点直径,F0为激光光斑中心处的能量密度,x为距离激光光斑中心的距离.相比与离焦激光加工(焦点位于加工平面上方),聚焦激光加工时(焦点位于加工平面下方),x逐渐减小,微孔孔壁上能受到更多的激光辐照,如图 10所示.当进给距离较小时,每个扫描层面可以受到更多的激光辐照,材料也可以得到充分去除.同时,同轴的辅助气体也能够及时地吹走淤积在加工区域的大量等离子体,进而有效削弱了等离子体屏蔽现象.
|
图 10 高斯光束加工示意 Figure 10 Schematic diagram of laser processing with Gaussian distribution |
根据Aldana等[20]的研究, 飞秒激光加工过程的饱和效应是不可忽视的[21].具有固定能量密度的多脉冲飞秒激光烧蚀金属时,会存在一个烧蚀深度极限.当其他参数固定时,扫描速度增加到一定程度,靶材的蚀除量不会继续增加.此时,增大扫描次数只会减小加工效率.此外,本文中应用的激光平均功率在同一数量级.相应的,单脉冲蚀除深度相差不大.在脉冲累积效应的作用下,加工区域的材料同样也能得到有效的去除.综合以上两方面分析可知,本文中扫描次数和激光平均功率对于加工微孔的形貌和精度的影响低于扫描速度和进给距离.
4 结论1) 结合Planck方程求解出不同脉宽飞秒激光作用下K24高温合金的吸收系数和反射率;用线性假设理论求解得出K24高温合金的晶格热容和电子比热.采用有限差分法求解一维双温模型,得出一定参数下加工过程中K24高温合金的电子与晶格温度分布,以及单脉冲飞秒激光的刻蚀深度.验证试验的结果与仿真求得的单脉冲蚀除深度能够较好地吻合,从而证明建立的理论模型的正确性以及线性假设理论在推导合金的一些物理参数中具有较高的可行性.
对四因素三水平正交试验结果进行效应曲线分析可知,扫描速度对于加工出的微孔的形貌影响最大,这是由于不同扫描速度引起的脉冲重叠度的变化以及脉冲累积效应.第二重要的因素是进给距离,这是由于较小的进给距离不仅可以提高不同扫描层面的蚀除量,同轴辅助气体也可以充分削弱等离子体屏蔽现象.由于饱和效应的存在以及使用的激光能量较低,本文中激光能量和扫描次数对于微孔形貌的影响不大.分析正交试验结果可以得出,较低的扫描次数,较小的进给距离,中等的扫描次数以及较高的激光平均功率可以高质量高效率的加工出微孔.
| [1] |
张昆, 陈济轮, 张晓阳. 镍基高温合金闭式叶轮高效加工工艺[J].
航天制造技术, 2012(5): 1-2, 13.
ZHANG K, CHEN J L, ZHANG X Y. High efficient machining technology of Nickel-based superalloy closed impeller[J]. Aerospace manufacturing technology, 2012(5): 1-2, 13. |
| [2] | KONG X J, YANG L J, ZHANG H Z, et al. Cutting performance and coated tool wear mechanisms in laser-assisted milling K24 nickel-based superalloy[J]. The International Journal of Advanced Manufacturing Technology, 2015, 77(9): 2151-2163. DOI: 10.1007/s00170-014-6606-9 |
| [3] | KRUGER J, KAUTEK W. Ultrashort pulse laser interaction with dielectrics and polymers[M]. [S.l.]: Springer Berlin Heidelberg, 2004:247-290. |
| [4] | WEI J, YE Y, SUN Z, et al. Control of the kerf size and microstructure in Inconel 738 superalloy by femtosecond laser beam cutting[J]. Applied Surface Science, 2016, 370: 364-372. DOI: 10.1016/j.apsusc.2016.02.162 |
| [5] | JIANG L, LIU P J, YAN X L, et al. High-throughput rear-surface drilling of microchannels in glass based on electron dynamics control using femtosecond pulse trains[J]. Optics letters, 2012, 37(14): 2781-2783. DOI: 10.1364/OL.37.002781 |
| [6] | ANISIMOV S. I, KAPELIOVICH B, PERELMAN T L. Electron emission from metal surfaces exposed to ultrashort laser pulses[J]. Zhurnal Eksperimentalnoi I Teoreticheskoi Fiziki, 1974, 66(776): 776-781. |
| [7] | KARIM E T, LIN Z B, ZHIGILEI L V. Molecular dynamics study of femtosecond laser interactions with Cr targets[C]// International Symposium on High Power Laser Abl. [S.l.]: American Institute of Physics, 2012:280-293. DOI: 10.1063/1.4739881. |
| [8] | POVARNITSYN, MIKHAIL E. Microscopic and macroscopic modeling of femtosecond laser ablation of metals[J]. Applied Surface Science, 2015, 357(3): 1150-1156. DOI: 10.1016/j.apsusc.2015.09.131 |
| [9] | ZHANG Y F, WANG L L, GONG J L. Numerical simulation of femtosecond laser multi-pulse ablation of Ni-Ti alloy[J]. Acta Photonica Sinica, 2016, 45(5): 003. DOI: 10.3788/gzxb20164505.0514002 |
| [10] | MA S, MCDONALD J, TRYON. P B, et al. Femtosecond laser ablation regimes in a single-crystal superalloy[J]. Metallurgical and Materials Transactions A, 2007, 38(13): 2349-2357. DOI: 10.1007/s11661-007-9260-0 |
| [11] | DAS D K, POLLOCK T M. Femtosecond laser machining of cooling holes in thermal barrier coated CMSX4 superalloy[J]. Journal of Materials Processing Technology, 2009, 209(15/16): 5661-5668. DOI: 10.1016/j.jmatprotec.2009.05.031 |
| [12] | WELLERSHOFF S S, HOHLFELD J, GUDDE J, et al. The role of electron-phonon coupling in femtosecond laser damage of metals[J]. Applied Physics A, 1999, 69(1): S99-S107. DOI: 10.1007/s003399900305 |
| [13] | NAKATA Y, TSUCHIDA K, MIYANAGA N. Nano-structured surfaces on Ni-Ti generated by multiple shots of interfering femtosecond laser[J]. Optics and Lasers in Engineering, 2009, 47(7/8): 847-849. DOI: 10.1016/j.optlaseng.2009.01.008 |
| [14] | GOYA K, ITOH T, SEKI A, et al. Efficient deep-hole drilling by a femtosecond, 400 nm second harmonic Ti:Sapphire laser for a fiber optic in-line/pico-liter spectrometer[J]. Sensors & Actuators B Chemical, 2015, 210: 685-691. DOI: 10.1016/j.snb.2014.12.115 |
| [15] | MA RK. Optical properties of solids[M]. Oxford: Oxford University Press, 2010. |
| [16] | SCHROEDER D V, PRIBRAM J K. An introduction to thermal physics[M]. Boston: Addison Wesley, 2000: 1284-1285. |
| [17] | YU C F, JINAG X F, CHENG P F, et al. Correlations among linear expansion coefficient, Debye temperature and Young modulus of metals[J]. Physics Experimentation, 2012(8): 013. |
| [18] | LIN Z B, ZHIGILEI L V. Temperature dependences of the electron-phonon coupling, electron heat capacity and thermal conductivity in Ni under femtosecond laser irradiation[J]. Applied Surface Science, 2007, 253(15): 6295-6300. DOI: 10.1016/j.apsusc.2007.01.032 |
| [19] | HILPERT K, MILLER M, GERADS H, et al. Thermodynamic study of the liquid and solid alloys of the Nickel-rich part of the Al-Ni phase diagram including the AlNi3 phase[J]. Zeitschrift für Elektrochemie, Berichte der Bunsengesellschaft für physikalische Chemie, 2010, 94(1): 40-47. DOI: 10.1002/bbpc.19900940109 |
| [20] | YANG L, WANG C Y, NI X C, et al. Microdroplet deposition of copper film by femtosecond laser-induced forward transfer[J]. Applied Physics Letters, 2006, 89(16): 161110-161110. DOI: 10.1063/1.2364457 |
| [21] | ALDANA J R V D, MENDEZ C, ROSO L. Saturation of ablation channels micro-machined in fused silica with many femtosecond laser pulses[J]. Optics Express, 2006, 14(3): 1329. DOI: 10.1364/OE.14.001329 |
 2017, Vol. 49
2017, Vol. 49


