2. 东北农业大学 水利与土木工程学院,哈尔滨 150030;
3. 东北林业大学 交通学院,哈尔滨 150040
2. School of Water Conservancy and Civil Engineering, Northeast Agricultural University, Harbin 150030, China;
3. Scholl of Traffic, Northeast Forestry University, Harbin 150040, China
在影响城市道路通行能力与服务水平的诸多因素中,平行式公交停靠将占用与停靠站邻近的车道从而形成瓶颈路段,对城市道路通行能力与服务水平的影响更严重,本文的研究对象即为平行式公交停靠影响下的城市干路通行能力计算与服务水平评价问题.
美国的道路通行能力手册[1]给出的城市道路路段通行能力计算方法较为简略,认为直行车道的通行能力等于1 800×(直行车车道数-1+最内侧直行车道未发生排队的概率),将城市道路路段服务水平划分为A~F 6级,评价指标为平均行程车速占自由流速度的比例.中国现行的规范[2]也只给出了城市道路路段的基本通行能力与设计通行能力推荐值,缺少对不同等级城市道路路段实际通行能力计算方法的规定,对于城市主、次干路也未给出服务水平的评价方法.
在分析停车对动态交通的影响方面,Christopher[3]对比分析了平行式和斜列式停车方式对道路交通流的不同阻滞特性及所产生事故率的差异. Koshy等[4]应用微观仿真模型研究了平行式和港湾式公交停靠对社会车辆运行速度的影响. Nagai等[5]基于车道变换分析了双车道道路由于公交停靠站引起的交通拥堵问题. Gu等[6]研究了信号交叉口上游直线式公交车停靠引起的排队问题.梁军等[7]针对双向两车道的道路采用路边垂直式停车方式的情况,建立了计算停车到达和出发导致路段交通流延误的模型.陈峻等[8]分别建立了设置路内停车带前后,机动车与非机动车车速与车流饱和度的关系模型,分析了路边平均停车次数和停放时间对车辆行驶速度的影响.杨晓光等[9]以公交进出停靠站对相邻车道的影响时间为基础,建立了公交影响时间模型.杨孝宽等[10]建立了港湾式与非港湾式两种停靠类型的公交到达频率与公交影响时间关系模型.在道路服务水平评价方面,除了HCM外的研究包括:Baumgaertner[11]的九个等级服务水平划分方法、Cameron[12]的10个等级服务水平划分方法. Levinson等[13]提出用延误指标(DRI)来评价道路拥挤状况.张雅静[14]研究了组团路网的服务水平评价问题.
综上所述,已有的道路通行能力与服务水平研究中对平行式公交停靠干扰的考虑较少,尤其是未考虑对不同车道的影响.而中国目前正在大力倡导公交优先政策,平行式公交停靠站也占有相当比例.在进行城市干路规划与设计过程中,通行能力计算与服务水平评价是车道数确定的重要依据,对于设置平行式公交停靠站的城市干路路段,其实际通行能力计算与服务水平评价研究值得开展深入的理论研究.
1 数据调查与分析 1.1 调查地点选择为了保证调查数据和建模精度,调查地点选择遵循了以下原则:1) 所选调查地点远离交叉口; 2) 避免调查范围内存在人行横道; 3) 避免道路纵坡坡度过大、车道宽度不足及路面不平整等的影响.
本次调查选取哈尔滨市15个位于主、次干路上的平行式公交停靠站,调查路段长度均在400 m以上,主干路双向6车道、机动车道宽21 m; 次干路双向4车道、机动车道宽度14 m.经过调查站点的公交线路较多,公交车排队形式为串连排列.调查与统计时段内路段机动车流为连续饱和车流,车头时距为饱和车头时距,调查得到的平均交通量为1 229 pcu/(h·ln).
1.2 调查内容与方法需要获取的数据包括:公交车停靠数量、平均行程车速、小客车饱和车头时距.需要注意的是,必须保证数据的同步性,即公交车停靠数量与平均行程车速、饱和车头时距同时观测.
本次调查采用视频观测法,在路段适当位置架设三脚架及摄像机,对路段的交通流和公交车停靠进行摄像记录.公交车停靠数量可由视频资料直接查取; 在调查路段上选取两个标志性的设施(调查时选取灯杆)并量取间距,平均行程车速通过车辆先后通过灯杆所用时间间接计算得出; 小客车饱和车头时距为饱和车流中前后车辆通过路段同一断面的时间差,采用表秒对视频资料进行观测获取.
1.3 数据分析对观测数据进行处理,得到调查路段内公交停靠数量与平均行程车速、小客车饱和车头时距数据,如表 1所示.其中,公交停靠数量为1 min内调查路段内的公交停靠数量,平均行程车速、小客车饱和车头时距为1 min内机动车流的平均饱和车头时距.
| 表 1 公交停靠数量与平均行程车速、小客车饱和车头时距数据 Table 1 Data of the number of stopping bus and average travel speed, cars' saturated headway |
对表 1中的数据进行分车道处理,得到邻近车道(与停靠站邻近的车道,即公交车行驶的车道)和间隔车道(与邻近车道相邻的车道)的平均行程车速、小客车饱和车头时距与公交车停靠数量的散点,如图 1~4所示.

|
图 1 邻近车道平均行程车速与公交停靠数量散点图 Figure 1 Scatter points of average travel speed on adjacent lane and the number of stopping bus |

|
图 2 间隔车道平均行程车速与公交停靠数量散点图 Figure 2 Scatter points of average travel speed on interval lane and the number of stopping bus |

|
图 3 邻近车道小客车饱和车头时距与公交停靠数量散点图 Figure 3 Scatter points of cars' saturated headway on adjacent lane and the number of stopping bus |
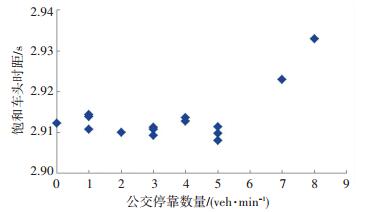
|
图 4 间隔车道小客车饱和车头时距与公交停靠数量散点图 Figure 4 Scatter points of cars' saturated headway on interval lane and the number of stopping bus |
从图 1和图 3中可以看出,随着公交停靠数量的增加,邻近车道的平均行程车速随之降低,小客车饱和车头时距随之增加.从图 2和图 4中可以看出,公交车停靠数量小于等于5 veh/min时,对间隔车道的平均行程车速和饱和车头时距影响不明显,公交停靠数量超过6 veh/min时,随着公交停靠数量的增加,车辆平均行程车速大幅降低,饱和车头时距明显增加.
分析间隔车道交通流参数的变化规律,在公交停靠数量较少( < 5 veh/min)时,邻近车道车辆由于受到的影响不显著,不会进行车道变化,从而对间隔车道的交通运行影响不明显; 而当公交停靠数量较多(超过5 veh/min)时,邻近车道车辆受公交停靠的影响已经严重到使其换道行驶,从而对间隔车道的交通运行产生显著影响.此外,对比分析邻近与间隔车道的平均行程车速、小客车饱和车头时距数据,可以发现:公交停靠数量相同的情况下,邻近车道的平均行程车速数据要比间隔车道小,小客车饱和车头时距要比间隔车道大,说明公交停靠对邻近车道的影响更明显.
2 关系模型构建 2.1 平均行程车速与公交停靠数量关系模型 2.1.1 邻近车道关系模型对图 1中的散点分别进行可能的函数关系拟合,得到邻近车道平均行程车速与公交停靠数量的关系函数式,见表 2.
| 表 2 邻近车道平均行程车速与公交停靠数量拟合函数 Table 2 Fitting functions of average travel speed on adjacent lane and the number of stopping bus |
在表 2中,二次函数的相关性最高,本文将其作为邻近车道平均行程车速与公交停靠数量的关系模型:
| $ {S_1} =-0.167\;5N_{\rm{b}}^2-0.710\;8{N_{\rm{b}}} + 41.87. $ | (1) |
式中:S1为邻近车道的平均行程车速,km/h; Nb为公交停靠数量,veh/min.
该模型的关系拟合曲线如图 5所示,其适用条件为Nb≤8 veh/min.

|
图 5 邻近车道平均行程车速与公交停靠数量拟合曲线 Figure 5 Fitting curve of average travel speed on adjacent lane and the number of stopping bus |
根据图 2中的散点分别进行可能的函数关系拟合,得到间隔车道平均行程车速与公交停靠数量的关系函数式,见表 3.由表 3可以看出,对间隔车道平均行程车速与公交停靠数量关系的拟合,二次函数的相关性更高,其关系拟合曲线如图 6所示.
| 表 3 间隔车道平均行程车速与公交停靠数量拟合函数 Table 3 Fitting functions of average travel speed on interval lane and the number of stopping bus |
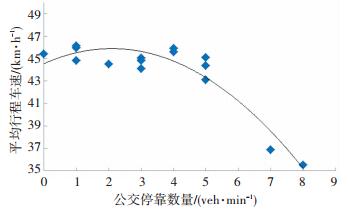
|
图 6 间隔车道平均行程车速与公交停靠数量拟合曲线 Figure 6 Fitting curve of average travel speed on interval lane and the number of stopping bus |
间隔车道小客车平均行程车速与公交停靠数量的关系模型为
| ${S_2} =-0305\;6N_{\rm{b}}^2 + 1.278\;5{N_{\rm{b}}} + 44.551. $ | (2) |
式中S2为间隔车道的平均行程车速,km/h.
定性分析模型应为单调递减函数,因此其适用条件为2 veh/min < Nb≤8 veh/min.
2.2 饱和车头时距与公交停靠数量关系模型 2.2.1 邻近车道关系模型根据图 3中的散点分别进行可能的函数关系拟合,得到邻近车道小客车饱和车头时距与公交停靠数量的关系函数式,见表 4.
| 表 4 邻近车道小客车饱和车头时距与公交停靠数量拟合函数 Table 4 Fitting functions of cars' saturated headway on adjacent lane and the number of stopping bus |
由表 4可以看出,对邻近车道小客车饱和车头时距与公交停靠数量关系的拟合,二次函数的相关性最高,其关系拟合曲线如图 7所示.

|
图 7 邻近车道小客车饱和车头时距与公交停靠数量拟合曲线 Figure 7 Fitting curve of cars' saturated headway on adjacent lane and the number of stopping bus |
邻近车道小客车饱和车头时距与公交停靠数量的关系模型为
| $ {h_{{\rm{s1}}}} = 0.006\;4N_{\rm{b}}^2-0.026\;5{N_{\rm{b}}} + 2.928\;2. $ | (3) |
式中hs1为邻近车道的小客车饱和车头时距,s.
定性分析模型应为单调递增函数,故其适用条件为Nb>2 veh/min.
2.2.2 间隔车道关系模型根据图 4中的散点分别进行可能的函数关系拟合,得到间隔车道小客车饱和车头时距与公交停靠数量的关系函数式,见表 5.
| 表 5 间隔车道小客车饱和车头时距与公交停靠数量拟合函数 Table 5 Fitting functions of cars' saturated headway on interval lane and the number of stopping bus |
由表 5可以看出,对于间隔车道饱和车头时距与公交车停靠数量关系的拟合,二次函数的相关性最高,其关系拟合曲线如图 8所示,间隔车道小客车饱和车头时距与公交停靠数量的关系模型为
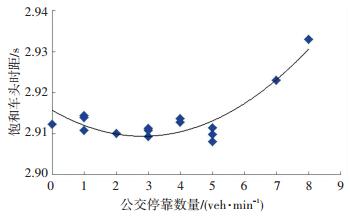
|
图 8 间隔车道小客车饱和车头时距与公交停靠数量拟合曲线 Figure 8 Fitting curve of cars' saturated headway on interval lane and the number of stopping bus |
| $ {h_{{\rm{s2}}}} = 0.000\;8N_{\rm{b}}^2-0.004\;5{N_{\rm{b}}} + 2.915\;7. $ | (4) |
式中hs2为间隔车道的小客车饱和车头时距, s.
定性分析模型应为单调增减函数,故其适用条件为Nb>2 veh/min.
3 考虑公交停靠影响的通行能力修正 3.1 实际通行能力计算道路通行能力是指道路的某一断面在单位时间内所能通过的最大车辆数,其计算式为
| $ C = \frac{{3\;600}}{{{h_{\rm{s}}}}}. $ | (5) |
式中:C为一条车道的通行能力,pcu/(h·ln); hs为小客车饱和流的车头时距,s.
通行能力可分为基本通行能力、实际通行能力和设计通行能力3种.基本通行能力是指在一定的时段及理想的道路、交通、控制和环境条件下,道路的一条车道或一断面,期望能通过的最大小时流率.现行规范中给出了城市干路一条车道的基本通行能力[2],对应设计速度60、50、40、30 km/h分别为1 800、1 700、1 650、1 600 pcu/ (h·ln).设计通行能力则是指设计道路组成部分在预计的道路、交通、管制及环境条件下,该组成部分一条车道或一断面,在规定运行条件下,能通过的最大小时流率.
实际通行能力是指在一定的时段,在具体的道路、交通、控制和环境条件下,道路的一条车道或一断面,期望能通过的最大小时流率.实际通行能力是评价现状道路服务水平的基础,需要在基本通行能力的基础上根据实际的交通运行环境进行修正,平行式公交停靠正是需进行修正的因素之一.
3.2 邻近车道通行能力修正根据式(3)、(5),可以得出平行式公交停靠影响下的邻近车道实际通行能力Cp1为
| $ {C_{{\rm{p1}}}} = \frac{{3\;600}}{{{h_{{\rm{s1}}}}}} = \frac{{3\;600}}{{0.006\;4N_{\rm{b}}^2-0.026\;5{N_{\rm{b}}} + 2.928\;2}}. $ | (6) |
根据式(6),可计算得到邻近车道实际通行能力的平行式公交停靠数量修正系数为
| $ {f_{{\rm{p1}}}} = \frac{{{C_{{\rm{p1}}}}}}{{{C_{\rm{b}}}}} = \frac{{3\;600}}{{\left( {0.006\;4N_{\rm{b}}^2-0.026\;5{N_{\rm{b}}} + 2.928\;2} \right) \times {C_{\rm{b}}}}}. $ | (7) |
式中:fp1为邻近车道实际通行能力的平行式公交停靠数量修正系数; Cb为一条车道的基本通行能力,pcu/ (h·ln),根据设计速度选取.
根据式(7),可计算得到不同设计速度的城市干路路段邻近车道实际通行能力的平行式公交停靠数量修正系数建议值,见表 6.
| 表 6 邻近车道不同公交停靠数量的修正系数建议 Table 6 Suggested adjustment factors for adjacent lane based on the number of stopping bus |
从表 6中可以看出,公交停靠数量相同的情况下,设计速度越低,邻近车道公交停靠数量修正系数越大,说明公交停靠对邻近车道交通运行的影响越不明显; 在相同设计速度下,公交停靠数量越多,修正系数呈逐渐变小趋势,说明公交停靠对邻近车道交通运行的影响越大.
3.3 间隔车道通行能力修正根据式(4)、(5),可以得出平行式公交停靠影响下的间隔车道实际通行能力Cp2为
| $ {C_{{\rm{p2}}}} = \frac{{3\;600}}{{{h_{{\rm{s2}}}}}} = \frac{{3\;600}}{{0.000\;8N_{\rm{b}}^2-0.004\;5{N_{\rm{b}}} + 2.915\;7}}. $ | (8) |
根据式(8),可计算得到间隔车道实际通行能力的平行式公交停靠数量修正系数fp2为
| $ {f_{{\rm{p2}}}} = \frac{{{C_{{\rm{p2}}}}}}{{{C_{\rm{b}}}}} = \frac{{3\;600}}{{\left( {0.000\;8N_{\rm{b}}^2-0.004\;5{N_{\rm{b}}} + 2.915\;7} \right) \times {C_{\rm{b}}}}}. $ | (9) |
根据式(9),可计算得到不同设计速度的城市干路路段间隔车道实际通行能力的平行式公交停靠数量修正系数建议值,见表 7.
| 表 7 间隔车道不同公交停靠数量的修正系数建议 Table 7 Suggested adjustment factors for interval lane based on the number of parallel stopping bus |
从表 7中可以看出,公交停靠数量相同的情况下,设计速度越低,间隔车道公交停靠数量修正系数越大,说明公交停靠对间隔车道交通运行的影响越不明显; 在相同设计速度下,公交停靠数量越多,修正系数呈逐渐变小趋势,说明公交停靠对间隔车道交通运行的影响越大.
3.4 实例验证如表 8所示,对本文的4个代表性调查路段(设计速度涵盖了规范取值,查表 6可知其基本通行能力)进行补充调查,得到平行式公交停靠数量、邻近车道与间隔车道的小客车饱和车头时距.
| 表 8 补充调查数据 Table 8 Supplementary survey data |
根据式(4),可计算得到邻近车道与间隔车道的实际通行能力; 查表 6、7可知邻近车道与间隔车道通行能力的公交停靠数量修正系数,根据基本通行能力,可求得其实际通行能力计算值,与根据实际观测值确定的实际通行能力进行比较分析,进而验证论文给出的计算方法与修正系数建议值,见表 9.
| 表 9 实际通行能力计算值与观测值对比 Table 9 Comparison between calculation and observation value of possible capacity |
从表 9中可以看出,采用本文所提出的修正系数计算平行式公交停靠干扰下城市干路路段的实际通行能力,与根据实际观测值确定的实际通行较为接近,邻近车道的计算误差为0.87%~1.77%,间隔车道计算误差为0.72%~2.46%.
4 基于公交停靠数量的服务水平评价 4.1 服务水平评价指标与划分标准鉴于现行规范并未给出城市主、次干路路段的服务水平评价指标与分级标准[2].因此,本论文参考美国道路通行能力手册中的基于城市道路路段服务水平分级标准的平均行程车速,如表 10所示[15].
| 表 10 美国城市道路服务水平分级表 Table 10 LOS classification of America |
从自由流速度来看,中国的主、次干路的速度值对应于美国城市道路的Ⅱ、Ⅲ、Ⅳ级.若对比表中典型自由流速度值与中国的主、次干路的设计速度值可以发现,中国的速度值较表 10中的典型自由流速度低5 km/h,因此,本文提出的基于城市道路路段服务水平划分标准的平均行程车速建议如表 11所示.
| 表 11 中国城市道路服务水平分级建议 Table 11 LOS classification suggestion of China |
根据式(1),可反算得到邻近车道对应不同平均行程车速的公交停靠数量计算式为
| $ {N_{\rm{b}}} = \frac{{-0.710\;8 + \sqrt {28.558\;1-0.67{S_1}} }}{{0.335}}. $ | (10) |
根据式(10),结合表 11,可计算得到平行式公交停靠干扰条件下,对应邻近车道不同服务水平等级的公交停靠数量阈值,见表 12.
| 表 12 平行式公交停靠数量对邻近车道服务水平影响阈值建议 Table 12 Suggested thresholds of the number of parallel stopping bus affecting LOS of adjacent lane |
根据式(2),可反算得到间隔车道对应不同平均行程车速的公交停靠数量计算式为
| $ {N_{\rm{b}}} = \frac{{1.278\;5 + \sqrt {55.737\;7-1.222\;4{S_2}} }}{{0.611\;2}}. $ | (11) |
根据式(11),结合表 11,可计算得到平行式公交停靠干扰条件下,对应间隔车道不同服务水平等级的公交停靠数量阈值,见表 13.
| 表 13 平行式公交停靠数量对间隔车道服务水平影响阈值建议 Table 13 Suggested thresholds of the number of parallel stopping bus affecting LOS of interval lane |
1) 平行式公交停靠对邻近车道与间隔车道的平均行程车速及饱和车头时距均有影响,但对间隔车道的影响要小于邻近车道,公交停靠数量与平均行程车速呈负相关二次函数关系,与小客车饱和车头时距呈正相关二次函数关系.
2) 计算城市干路路段实际通行能力,需考虑平行式公交停靠的影响,邻近车道与间隔车道的公交停靠数量修正系数均随设计速度的提高与停车数量的增加逐渐变小.实例验证表明,应用所提出的城市干路路段实际通行能力的公交停靠数量修正系数建议值,可以较为准确地计算城市干路路段邻近车道与间隔车道的实际通行能力.
3) 平行式公交停靠干扰条件下城市道路路段的服务水平会下降,在理论建模的基础上,给出了划分城市干路路段服务水平等级的平行式公交停靠数量阈值建议,可以根据公交停靠数量较为简易地评价邻近车道与间隔车道的服务水平.鉴于中国的相关规范尚未有相关规定,借鉴了美国的研究成果,故所提出的研究成果应为探索性的建议.
| [1] |
Tranportation Research Board.
Highway capacity manual[M]. 5th ed. Washington DC: National Academy of Sciences, 2010: 16-17.
|
| [2] |
中华人民共和国住房和城乡建设部. 城市道路工程设计规范: CJJ 37—2012[S]. 北京: 中国建筑工业出版社, 2012.
|
| [3] |
CHRISTOPHER M M. Safety comparison of angle and parallel parking: TRA 07-01-05[R]. Salem: Oregon Department of Transportation, 2001.
|
| [4] |
KOSHY R Z, ARASAN V T. Influence of bus stops on flow characteristics of mixed traffic[J].
Journal of Transportation Engineering, 2005, 131(8): 640-643.
DOI: 10.1061/(ASCE)0733-947X(2005)131:8(640) |
| [5] |
NAGAI R, NAGATANI T, TANIGUCHI N. Traffic states and jamming transitions induced by a bus in two-lane traffic flow[J].
Physica A, 2005, 350(2): 548-562.
DOI: 10.1016/j.physa.2004.10.025 |
| [6] |
GU W, CASSIDY M J, GAYAH V V, et al. Mitigating negative impacts of near-side bus stops on cars[J].
Transportation Research Part B, 2013, 47(1): 42-56.
DOI: 10.1016/j.trb.2012.09.005 |
| [7] |
梁军, 李旭宏, 于洪君, 等. 路边停车对路段交通流的影响研究[J].
公路交通科技, 2003, 20(2): 85-87.
LIANG Jun, LI Xuhong, YU Hongjun, et al. Study on road traffic delay caused by roadside parking[J]. Journal of Highway and Transportation Research and Development, 2003, 20(2): 85-87. |
| [8] |
陈峻, 王炜, 梅振宇. 路边停车带设置对混合车流速度影响分析[J].
交通运输系统工程与信息, 2005, 5(5): 34-36.
CHEN Jun, WANG Wei, MEI Zhenyu. The analysis on speed of mixed traffic flow with the curb parking lots[J]. Journal of Transportation Systems Engineering and Information Technology, 2005, 5(5): 34-36. |
| [9] |
杨晓光, 徐辉, 龙科军, 等. 公交停靠站对相邻车道通行能力的影响[J].
系统工程, 2008, 27(8): 74-79.
YANG Xiaoguang, XU Hui, LONG Kejun, et al. The effects of bus stops on capacity of neighboring lanes[J]. Systems Engineering, 2008, 27(8): 74-79. |
| [10] |
杨孝宽, 曹静, 宫建. 公交停靠站对基本路段通行能力影响[J].
北京工业大学学报, 2008, 34(1): 65-71.
YANG Xiaokuan, CAO Jing, GONG Jian. Study of the effect of bus stop on roadway section capacity[J]. Journal of Beijing University of Technology, 2008, 34(1): 65-71. |
| [11] |
BAUMGAERTNER W E. Level of Service-getting ready for the 21st century[J].
ITE Journal, 1996, 66(1): 36-39.
|
| [12] |
CAMERON R. An expanded LOS gradation system[J].
ITE Journal, 1996, 66(1): 40-41.
|
| [13] |
LEVINSON H S, LOMAX T J. Developing a travel time congestion index[J].
Transportation Research Record, 1996, 1564(1): 1-10.
DOI: 10.3141/1564-01 |
| [14] |
张雅静. 城市组团路网服务水平评价研究[D]. 重庆: 重庆交通大学, 2015.
ZHANG Yajing. Study on the service level evaluation of road network [D]. Chongqing: Chongqing Jiaotong University, 2015. http://d.wanfangdata.com.cn/Thesis/Y2809041 |
| [15] |
Tranportation Research Board.
Highway capacity manual[M]. 4th ed. Washington DC: National Academy of Sciences, 2000: 15-31.
|
 2017, Vol. 49
2017, Vol. 49


