滚动轴承故障诊断方法一直是国内外研究的热点.滚动轴承运行过程中的振动信号往往包含着重要的运行状态信息[1-3].因此,目前应用最为普遍的轴承故障诊断方法是通过提取轴承振动信号中的故障特征后,利用模式识别方法实现故障识别[2].然而,滚动轴承振动信号具有非线性与非平稳性的特点,并且在传输过程中容易受到背景噪声以及其他运动部件的影响,导致从原始振动信号中提取出故障特征变得十分困难[3, 22-23],进而严重影响故障识别的准确率.传统的时-频分析方法在轴承故障诊断中有较多的应用也取得了相应的成果,如短时傅里叶变换[4]、小波变换[2]等.但以上方法都存在着对轴承振动信号分解缺乏自适应能力的缺陷.对于复杂的故障振动信号,仅仅依靠人的主观参数设置来进行分解,可能会造成故障特征信息的遗漏,严重影响故障诊断的性能[5].
经验模态分解(empirical mode decomposition, EMD)[6]是最具代表性的自适应时—频分析方法之一,并且已经在传感器信号处理、机械故障诊断等很多领域得到了应用[7-8].然而,由于EMD存在模态混淆现象,会在一定程度上影响信号分解的效果,导致分解结果不稳定[9],进而影响后续特征提取的结果.因此,本文利用文献[10]提出的集合经验模态分解(ensemble EMD, EEMD)的方法,利用噪声辅助分析方法抑制模态混叠现象,改善EMD的信号分解能力.针对于轴承振动信号包含信息丰富、成分复杂的特点,利用EEMD自适应地将轴承振动信号分解为一系列本征模态函数(intrinsic mode functions,IMFs),减少不同故障信号特征信息之间的干涉或耦合,有利于突出轴承运行状态更深层次的信息[11].
排列熵(permutation entropy, PE)作为一种衡量一维时间序列复杂度的平均熵参数,不仅能够度量一个非线性信号的不确定性,而且具有计算简单,抗噪声能力强等优点[12],选择排列熵对IMFs中包含的故障特征进行提取, EEMD分解后得到的每个IMF分量包含了振动信号在不同时间尺度下的特征.通过计算各个IMF分量的排列熵值并组成特征向量,能够有效突出在多尺度下的轴承故障特征.
在对不同故障情况下的特征向量进行有效提取后,需要利用高性能的多分类器对故障模式进行识别.相关向量机(relevance vector machine, RVM)和支持向量机(support vector machines, SVM)是机械故障诊断中常用的分类器. RVM是由Micnacl E. Tipping[13]提出的一种与SVM类似的稀疏概率模型,是一种基于贝叶斯网络的新的监督学习方法.
多分类相关向量机(multiclass relevance vector machine, M-RVM)[14]是RVM算法针对多分类应用场合下的理论扩展,该方法继承了RVM算法模型稀疏度高、小样本学习能力强及分类速度快的优点,通过不同类别的概率输出直接实现多分类,有效降低了基于RVM分类器进行多分类时结构的复杂性.
本文针对目前基于模式识别的轴承故障诊断方法存在的问题,提出了一种基于EEMD-排列熵特征提取与M-RVM分类器相结合的轴承故障诊断方法.首先利用EEMD将滚动轴承振动信号自适应地分解为一系列IMFs,采用排列熵提取各个IMF的特征值,组成特征向量.为了突出主要的故障特征,通过计算包含主要故障信息的前几个IMFs分量的排列熵值来组成特征向量.利用不同故障下训练样本的特征向量对M-RVM分类器进行建模,最后以概率输出的形式实现对故障轴承振动信号的多故障识别,实现滚动轴承的故障诊断.
1 轴承振动信号特征提取 1.1 基于EEMD的轴承振动信号分解振动是滚动轴承运行过程中的重要特征,振动信号能够体现滚动轴承运行过程中的状态信息.通过对滚动轴承振动信号进行分解,提取轴承运行状态中的故障特征,为轴承故障诊断提供信息.由于故障轴承的振动信号在某一频率上包含故障信息,采用时-频分析法对轴承振动信号进行分解.
传统的EMD分解存在着模态混叠问题,会导致分解出的本征模态函数的物理意义不明确,影响后续的特征提取效果.针对以上问题,文献[10]提出了EEMD算法,该方法通过在原始信号上叠加一定幅值的高斯白噪声,利用其统计特性解决EMD算法的模态混叠问题,使得EEMD分解得到的本征模态函数更加稳定.因此,本文采用EEMD对轴承振动信号进行自适应分解以突出故障在各个频带上的特征.
基于EEMD算法的滚动轴承振动信号分解过程的具体步骤如下:
1) 指定EEMD算法的总体平均次数M以及高斯白噪声的幅值a.
2) 在原始的振动信号x(t)上叠加幅值为a的随机高斯分布的白噪声ni(t),获得一个新的信号, 即
| $ {x_i}\left( t \right) = x\left( t \right) + {n_i}\left( t \right). $ | (1) |
其中i=1, 2, …, M,ni(t)为第i次加入的白噪声序列,xi(t)为第i次叠加白噪声后得到的新信号.
3) 对由步骤2获得的新信号xi(t)进行EMD分解,得到一组本征模态函数IMFs以及一个残余分量, 即
| $ {x_i}\left( t \right) = \sum\limits_{s = 1}^S {{{\rm{C}}_{i,s}}\left( t \right) + {r_i}\left( t \right)} . $ | (2) |
其中S为分解出的IMF分量的总数,ri(t)为残余分量,(Ci, 1(t), Ci, 2(t), …, Ci, S(t))为包含着从高频到低频的的本征模态函数.
4) 根据步骤1中设置的总体平均次数M,重复第2、3步M次,获得M组本征模态函数.
5) 将步骤4中获得的M组本征模态函数进行总体平均,即
| $ {C_S}\left( t \right) = \frac{1}{M}\sum\limits_{i = 1}^M {{\rm{IM}}{{\rm{F}}_{i,S}}\left( t \right)} . $ | (3) |
其中CS(t)为EEMD分解后的第S个IMF向量,i=1, 2, …, M并且s=1, 2, …, S.
EEMD利用大量不同的白噪声信号的均值将趋于0的特性,通过多次重复步骤2、3,将叠加的白噪声对信号的不利影响从平均后的IMF分量中剔除,保留了目标信号的分解结果,提高了信噪比.与单次EMD分解相比,显著减少了模态混叠的发生,能更准确地揭示信号的真实物理意义.基于以上考虑,本文选择EEMD进行滚动轴承振动信号的分解.通过对以上EEMD算法的实现步骤可知,总体平均次数M与白噪声幅值a是影响分解结果的两个重要参数.文献[4]表明,白噪声幅值a取值约为0.2~0.4倍的原始数据标准差,总体平均次数M=100~500时,EEMD具有较好的分解结果.
1.2 基于排列熵的轴承振动信号特征提取通过上一节介绍的EEMD可以对轴承振动信号进行自适应分解,分解得到的本征模态函数与残余分量中包含不同故障类型的频率特征.为了突出不同故障类型的特征,本节采用排列熵对轴承振动信号进行特征提取.排列熵是由Christoph Band[16]提出的是一种时间序列复杂性衡量方法.对于长度为N的时间序列{x(k), k=1, 2, …, N},按照相空间延迟坐标法,对任一元素x(i)其进行重构,对每个采样点取其连续的m个样本点,得到点x(i)的m维重构向量
| $ X\left( i \right) = \left\{ {x\left( i \right),x\left( {i + \tau } \right), \cdots ,x\left( {i + \left( {m - 1} \right)\tau } \right)} \right\}\frac{1}{n}. $ | (4) |
其中m≥2为嵌入维数,τ为延迟时间,i=1, 2, …, N.将X(i)中的m个重构分量按照升序排列,即
| $ \begin{array}{*{20}{c}} {\left\{ {x\left( {i + \left( {{j_1} - 1} \right)\tau } \right) \le x\left( {i + \left( {{j_2} - 1} \right)\tau } \right) \le } \right.}\\ {\left. { \cdots \le x\left( {i + \left( {{j_m} - 1} \right)\tau } \right)} \right\}.} \end{array} $ | (5) |
如果X(i)存在相同的元素,即x(i+(jp-1)τ)=x(i+(jq-1)τ)时,那么按照j的大小来排序,也就是p≤q时,排列方式为x(i+(jp-1)τ)≤x(i+(jq-1)τ).
因此,任意向量X(i)都能得到一组符号序列
| $ S\left( l \right) = \left( {{j_1},{j_2}, \cdots ,{j_m}} \right). $ | (6) |
其中: j=1, 2, …, k,与m维相空间映射的m个不同的符号序列具有m!种不同的排列方式,而S(l)=(j1, j2, …, jm)是其中的一种符号序列,设每种符号序列出现的概率分别为P1, P2, …, Pk,时间序列{x(k), k=1, 2, …, N}的排列熵定义为
| $ {H_p}\left( m \right) = - \sum\limits_j^k {{P_j}\ln {P_j}} . $ | (7) |
很明显,0≤Hp(m)≤ln(m!),其中上限ln(m!)为Pj=1/m!时对应的Hp(m)值.
通过值Hp的大小就能够衡量出一维时间序列{x(k), k=1, 2, …, N}的复杂程度. Hp值越小,则该时间序列越规则,信号复杂度越小;相反的,Hp值越大,则该时间序列无序程度越高,信号复杂度越大.
由排列熵的计算过程看出,排列熵的值与嵌入维数m,延迟时间τ以及数据长度N有关.文献[18]表明,嵌入维数m=4~8时,4种工作状态的区分度良好,实际上当嵌入维数m<4时,排列熵无法准确地检测出振动信号中的动态变化,而当m>8时,不仅会使排列熵的计算量增大,并且会使排列熵的的变化范围变窄而难于准确衡量信号复杂度.延迟时间τ的选取对排列熵的影响不大.但是,当τ>5时,排列熵不能准确地检测振动信号中的微小变化.数据长度N也是影响排列熵计算结果的重要参数,N过大时会将信号平滑,不能准确的衡量信号的动态变化. N取过小的值,计算结果将失去统计意义.
2 基于多分类相关向量机的故障识别M-RVM是在RVM的基础上提出的一种基于贝叶斯框架的统计学习方法[14],它采用分层贝叶斯模型结构,通过引入多项概率似然函数来实现多分类以及输出类别成员概率.通过采集不同故障条件下的振动信号作为训练样本,结合上一节介绍的特征提取方法对M-RVM故障识别模型进行训练.基于M-RVM的故障识别模型的建模过程如下.
设训练集X={xi, ti}i=1N,x∈RD,t∈{1, 2, …, C}为类别标签,当选定核函数时,可以得到训练核函数集K=(k1, …, kN)T,K∈RN×N,其中
| $ {y_{nl}}\left| {{w_l},{k_n}} \right. \sim {N_{{y_{nl}}}}\left( {{k_n}{w_l},1} \right). $ | (8) |
式中ynl为Y的第n行l列的元素,wl为W的第l列,Nx(m, v)表示x服从均值为m,方差为v的正态分布.
回归目标可以通过式tn=i,yni>ynj, ∀j≠i将回归目标转化为类别标签.
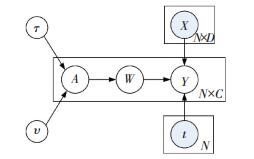
为了保证模型的稀疏性,为权重向量引入均值为0,方差为αnl-1的标准正态先验分布.由先验参数αnc组成的矩阵记为A∈RN×L,服从超参数为αnl的Gamma分布.由此可见M-RVM采用的是分层贝叶斯模型结构,模型结构示意图如图 1所示.
|
图 1 M-RVM模型结构示意 Figure 1 Structure diagram of M-RVM |
由此,可以推导出后验概率
| $ \begin{array}{l} P\left( {\boldsymbol{W}\left| \boldsymbol{Y} \right.} \right) \propto P\left( {\boldsymbol{Y}\left| \boldsymbol{W} \right.} \right)P\left( {\boldsymbol{W}\left| \boldsymbol{A} \right.} \right) \propto \\ \;\;\;\;\prod\limits_{c = 1}^C {N\left( {{{\left( {\boldsymbol{K}{\boldsymbol{K}^T} + {\boldsymbol{A}_c}} \right)}^{ - 1}}K\boldsymbol{y}_c^T,{{\left( {\boldsymbol{K}{\boldsymbol{K}^T} + {\boldsymbol{A}_c}} \right)}^{ - 1}}} \right)} . \end{array} $ | (9) |
其中Ac为由A的c列导出的对角阵.
由最大后验概率估计可得
| $ \hat W = \arg {\max _W}P\left( {\boldsymbol{W}\left| {\boldsymbol{Y},\boldsymbol{A},\boldsymbol{K}} \right.} \right). $ | (10) |
因此,当给定类别时,基于最大后验估计的权重更新方式为
| $ {{\hat w}_c} = {\left( {\boldsymbol{K}{\boldsymbol{K}^T} + {\boldsymbol{A}_c}} \right)^{ - 1}}\boldsymbol{Ky}_c^T. $ | (11) |
最后,权重向量先验参数的后验概率分布为
| $ \begin{array}{*{20}{c}} {P\left( {\boldsymbol{A}\left| {\left. \boldsymbol{W} \right)} \right.} \right) \propto P\left( {\left| \boldsymbol{W} \right|\boldsymbol{A}} \right)P\left( {\boldsymbol{A}\left| {\tau ,\upsilon } \right.} \right) \propto }\\ {\prod\limits_{c = 1}^C {\prod\limits_{n = 1}^N {G\left( {\tau + \frac{1}{2},\frac{{w_{nc}^2 + 2\boldsymbol{\upsilon }}}{2}} \right)} } .} \end{array} $ | (12) |
利用式(12)就可以计算出测试信号属于不同类型的概率,测试信号对应的概率最高的一类,即为测试信号的归属.
3 提出的故障诊断方法流程本文通过集合经验模态分解法对非线性、非平稳信号的自适应能力解决小波分析、短时傅里叶变换等传统时-频分析方法适应性较差的问题.在对经EEMD分解得到的本征模态函数包含故障信息进行有效分解的基础上,采用排列熵提取轴承故障状态下的故障特征向量.在对故障特征有效提取的基础上,利用M-RVM分类器的良好特性实现对故障的识别.在此基础上,设计了基于EEMD-排列熵特征提取与M-RVM分类器相结合的滚动轴承故障诊断方法流程如图 2所示.

|
图 2 基于EEMD-排列熵与M-RVM的滚动轴承故障诊断流程 Figure 2 Flow of rolling bearing fault diagnosis based on EEMD-PE coupled with M-RVM |
可以看出提出的轴承故障诊断方法存包括两个步骤:训练过程和测试过程.具体过程如下:1)获取不同故障状态下原始轴承振动信号分割为互不重叠的子样本,组成训练样本集与测试样本集. 2)对训练样本集中各故障模式的信号进行特征提取.利用EEMD分解故障信号,获得若干个本征模态函数,选择前p个包含大量故障信息的本征模态函数作为特征提取的对象. 3)计算每个训练样本中选取的各本征模态函数的排列熵,并组成p维特征值向量,完成训练样本特征提取. 4)选取适当的核函数以及核参数,利用训练样本的特征向量对M-RVM分类器进行训练. 5)在测试过程中,将测试样本经EEMD-排列熵特征后的特征向量作为M-RVM分类模型的输入,利用输出各类别的概率来确定滚动轴承的故障模式,实现故障识别.
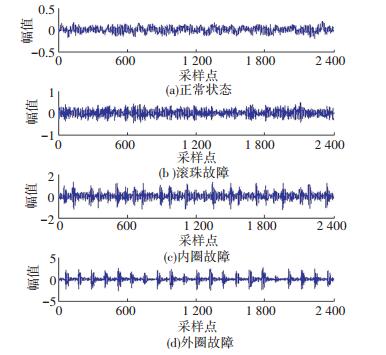
4 实验结果 4.1 实验数据为了说明本文提出的基于EEMD-排列熵特征提取与M-RVM分类器相结合的滚动轴承故障诊断方法的性能,本文采用美国西储大学轴承数据库(Case Western Reserve University,CWRU)[17]发布的公共数据集.被测试轴承通过电火花加工技术设置单点故障,数据集中包括四种滚动轴承运行状态下获得的振动信号,分别为正常(normal,N),滚珠故障(ball fault,BF),内圈故障(inner race fault,IRF)以及外圈故障(outer race fault,ORF),4种工作状态下的振动信号样本,时域波形如图 3所示.
|
图 3 负载为0 kW时不同轴承状态下采集的振动信号 Figure 3 Vibration signals under different modes with 0 kW |
每种状态下采集到的信号又按照故障直径与负载的大小进行分类.本文选取CWRU数据集中的各个样本进行轴承故障诊断实验,采样频率为12 kHz.实验包含的所有样本如表 1所示,其中“√”代表该样本被选取,“*”代表着该样本未选取.按照负载的不同,可以将实验分为4组,每组实验所用数据按照故障类型及故障直径分类共有12种.由于实际状况下,轴承发生故障时故障程度不可知,因此本文将故障直径不同,故障类型相同的数据归为一类,即负载相同的12种数据按照故障类型的不同总共归为4类.每种数据的前120 000个点,分割成50个长度为2 400的子样本,因此每组实验中共包含了600个样本,其中正常状态下的样本数为50个,随机选取20组作为训练数据.外圈故障的样本数为150个,随机选取60组作为训练数据.其余两种状态的样本数都是200个,分别随机选取80组作为训练数据,其余的所有样本作为测试样本.
| 表 1 不同负载下的实验样本 Table 1 Experimental samples under different loads |
随机选取负载为0 kW,故障直径为0.018 cm时4个状态下的一个样本,利用EEMD对其进行分解,得到一组IMF分量,本文选取的白噪声幅值为原始信号标准差的0.2倍,总体平均次数为100次.然后选取排列熵的参数为m=6,τ=2,计算各个状态下分解得到的前6个IMF分量的排列熵.如图 4所示,可以看出,前4个本征模态分量几乎包含了振动信号的最主要的信息,并且不同状态计算出的本征模态分量排列熵值差异较大,对故障分类的贡献也较大.这是由于包含轴承故障特征的频率主要集中在中高频段,只取前4个IMF分量来提取特征值.

|
图 4 不同故障状态下的本征模态排列熵值 Figure 4 PE values of IMFs under different fault modes |
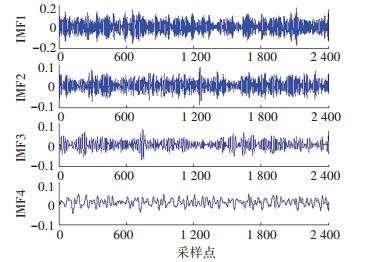
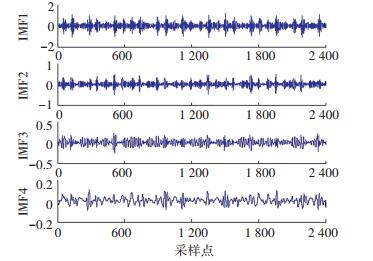
各类样本分解后的前4个IMF分量如图 5~8所示.其中,图 5是正常状态下采集的振动信号的分解结果,图 6是滚珠故障状态下采集的振动信号的分解结果,图 7是内圈状态下采集的振动信号的分解结果,图 8是外圈故障状态下采集的振动信号的分解结果.从图 5~8可以看出,不同状态下采集的振动信号分解出的各个IMF分量有着明显的差异,相对于原始信号,能够展示更多的特征信息.

|
图 5 正常样本的EEMD分解结果 Figure 5 EEMD decomposition results of normal samples |
|
图 6 滚珠故障样本的EEMD分解结果 Figure 6 EEMD decomposition results of balls fault samples |
|
图 7 内圈故障样本的EEMD分解结果 Figure 7 EEMD decomposition results of inner race fault samples |

|
图 8 外圈故障样本的EEMD分解结果 Figure 8 EEMD decomposition results of outer race fault samples |
接下来计算EEMD分解后的前4个IMF分量的排列熵,组成4维的特征向量v=[d1, d2, d3, d4]用来描述轴承不同状态下的特征.负载为0 kW时,不同轴承状态以及故障直径的样本数据的特征向量见表 2.提取的4个特征在数值上具有一定的可分性,说明本文提出的基于EEMD-PE的故障特征提取方法具有明显的可分性.
| 表 2 轴承不同状态以及不同故障直径的样本特征向量 Table 2 Feature vectors of rolling bearing under different fault modes and severity |
决定M-RVM分类准确性的关键因素是在训练阶段选取合适的核函数以及核参数.鉴于径向基核函数(radial basis function,RBF)高维/低维、线性/非线性信号的优良特性,本文实验中选择RBF核函数为M-RVM分类器的核函数,即
| $ K\left( {x,y} \right) = \exp \left( { - \frac{{{{\left\| {x - y} \right\|}^2}}}{{2{\sigma ^2}}}} \right). $ | (13) |
其中核参数σ的选择利用交叉验证法,选取诊断准确度最高的时候对应的取值.
M-RVM通过输出不同故障类型可能发生故障的概率进行故障诊断,其中对应着概率最大的故障类型被确定为最终诊断结果. 表 3为负载为0 kW时不同样本的M-RVM故障识别结果,其中Class1,Class2,Class3和Class4分别代表属于正常状态,滚珠故障,内圈故障以及外圈故障,P1~P4表示对应着不同故障类型Class1~Class4的M-RVM模型的输出概率.实验结果说明,M-RVM能够有效地对不同状态下的故障特征进行分类,准确率达到90.0%以上,具有较高的置信度.
| 表 3 负载为0 kW时不同样本的M-RVM故障识别结果 Table 3 Fault identification results based on M-RVM under different fault modes with 0 kW load |
应用EEMD分解后的前4个IMF分量的排列熵值组成特征向量,对数据集进行训练与测试,每组实验重复10次,取其诊断结果的平均值作为故障诊断结果并记录.故障分类结果见表 4.可以看出,利用本文提出的故障诊断方法具有较高的故障识别率,适用于不同负载情况下的滚动轴承故障诊断.
| 表 4 不同负载情况下轴承故障分类准确率 Table 4 Fault identification accuracy of rolling bearing under different loads |
为了进一步的验证所提方法的故障诊断效果,将本文的故障诊断方法与现有方法的实验结果进行对比,结果如表 5所示.实验结果表明,相比于现有的轴承故障诊断方法,本文提出的故障诊断方法具有更高的故障识别率.
| 表 5 故障诊断方法比较 Table 5 Experiment comparison of different fault diagnosis methods of rolling bearing |
提出了一种基于EEMD-排列熵特征提取与M-RVM分类器相结合的滚动轴承故障诊断新方法,将EEMD与排列熵算法进行特征提取,并与M-RVM方法融合在一起进行故障诊断.首先,采用EEMD分解将轴承振动信号自适应地分解为一系列包含故障特征的IMF分量,再计算IMF分量的排列熵作为特征向量,提高特征向量的可分性.随后,采用M-RVM分类器作为故障识别方法对滚动轴承进行故障识别,利用概率输出实现故障识别.实验结果表明,所提出的方法能够在不同负载下有效地对轴承故障类型进行识别,与现有基于模式识别的故障诊断方法相比,具有更高的故障识别准确率.
| [1] |
FENG Z, LIANG M, CHU F. Recent advances in time-frequency analysis methods for machinery fault diagnosis: a review with application examples[J].
Mechanical Systems & Signal Processing, 2013, 38(1): 165-205.
|
| [2] |
徐金梧, 徐科. 小波变换在滚动轴承故障诊断中的应用[J].
机械工程学报, 1997(4): 50-55.
XU Jinwu, XU Ke. Appilication of wavelet transform in failure diagnosis of rolling bearings[J]. Journal of Mechanical Engineering, 1997(4): 50-55. |
| [3] |
ZHANG L, XIONG G, LIU H, et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference[J].
Expert Systems with Applications, 2010, 37(8): 6077-6085.
DOI: 10.1016/j.eswa.2010.02.118 |
| [4] |
彭畅, 柏林, 谢小亮. 基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J].
振动与冲击, 2012(20): 143-146.
PENG Chang, BO Lin, XIE Xiaoliang. Fault diagnosis method of rolling element bearing based on EEMD, measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012(20): 143-146. |
| [5] |
李舜酩, 郭海东, 李殿荣. 振动信号处理方法综述[J].
仪器仪表学报, 2013, 34(8): 1907-1915.
LI Shunming, GUO Haidong, LI Dianrong. Review of vibration signal processing methods[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1907-1915. |
| [6] |
HUANG N E, SHEN Z, LONG S R, el al. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis[J].
Proceedings of the Royal Society of London A, 1998, 454(1971): 903-995.
DOI: 10.1098/rspa.1998.0193 |
| [7] |
XU H B, CHEN G H. An intelligent fault identification method of rolling bearings based on LSSVM optimized by improved PSO[J].
Mech Syst Signal Process, 2013, 35(1/2): 167-175.
|
| [8] |
陈寅生, 姜守达, 刘晓东, 等. 基于EEMD样本熵和SRC的自确认气体传感器故障诊断方法[J].
系统工程与电子技术, 2016, 38(5).
CHEN Yinsheng, JIANG Shouda, LIU Xiaodong, et al. Self-validating gas sensor fault diagnosis method based on EEMD sample entropy and SRC[J]. Systems Engineering and Electronics, 2016, 38(5). DOI: 10.3969/j.issn.1001-506X.2016.05.01 |
| [9] |
WANG H, CHEN J, DONG G. Feature extraction of rolling bearing's early weak fault based on EEMD and tunable Q-factor wavelet transform[J].
Mechanical Systems & Signal Processing, 2014, 48(1/2): 103-119.
|
| [10] |
WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J].
Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
DOI: 10.1142/S1793536909000047 |
| [11] |
赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法[J].
振动与冲击, 2012, 31(6): 136-140.
ZHAO Zhihong, YANG Shaopu. Sample entropy based roller fault diagnosis method[J]. Journal of Vibration and Shock, 2012, 31(6): 136-140. |
| [12] |
程军圣, 马兴伟, 杨宇. 基于排列熵和VPMCD的滚动轴承故障诊断方法[J].
振动与冲击, 2014, 33(11): 119-123.
CHENG Junsheng, MA Xingwei, YANG Yu. Rolling fault diagnosis method based on permutation entropy and VPMCD[J]. Journal of Vibration and Shock, 2014, 33(11): 119-123. |
| [13] |
TIPPING M E. The relevance vector machine[J].
Advances in Neural Information Processing Systems, 1999, 12(3): 652-658.
|
| [14] |
PSORAKIS I, DAMOULAS T, GIROLAMI M A. Multiclass relevance vector machines: sparsity and accuracy[J].
IEEE Transactions on Neural Networks, 2010, 21(10): 1588-1598.
DOI: 10.1109/TNN.2010.2064787 |
| [15] |
ZHANG X, ZHOU J. Multi-fault diagnosis for rolling element bearings based on ensemble empirical mode decomposition and optimized support vector machines[J].
Mechanical Systems & Signal Processing, 2013, 41(1/2): 127-140.
|
| [16] |
CHRISTOPH B, BERND P. Permutation entropy: a natural complexity measure for time series[J].
Physical Review Letters, 2002, 88(17): 174102.
DOI: 10.1103/PhysRevLett.88.174102 |
| [17] |
Bearing Data Center. Case Western Reserve University. (2000-01-31). http://csegroups.case.edu/bearingdatacenter/home.
|
| [18] |
刘永斌. 基于非线性信号分析的滚动轴承状态监测诊断研究[D]. 合肥: 中国科学技术大学, 2011.
LIU Yongbin.Nonlinear signal analysis for rolling bearing condition monitoring and fault diagnosis [D]. Hefei: Universitity of Science and Technology of China, 2011. http: //cdmd. cnki. com. cn/article/cdmd-10358-1011125017. htm |
| [19] |
WU S D, WU C W, WU T Y, et al. Multi-scale analysis based ball bearing defect diagnostics using mahalanobis distance and support vector machine[J].
Entropy, 2013, 15(2): 416-433.
DOI: 10.3390/e15020416 |
| [20] |
LIU Z, CAO H, CHEN X, et al. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings[J].
Neurocomputing, 2013, 99(1): 399-410.
|
| [21] |
VAKHARIA V, GUPTA V K, KANKAR P K. A multiscale permutation entropy based approach to select wavelet for fault diagnosis of ball bearings[J].
Journal of Vibration & Control, 2014, 21(16).
|
| [22] |
于天剑, 陈特放, 陈雅婷, 等. HMM在电机轴承上的故障诊断[J].
哈尔滨工业大学学报, 2016, 48(2): 184-188.
YU Tianjian, CHEN Tefang, CHEN Yating, et al. HMM on the motor bearing fault diagnosis[J]. Journal of Harbin Institute of Technology University, 2016, 48(2): 184-188. DOI: 10.11918/j.issn.0367-6234.2016.02.032 |
| [23] |
李常有, 徐敏强, 高晶波, 等. 基于独立分量分析的滚动轴承故障诊断[J].
哈尔滨工业大学学报, 2008, 40(9): 1363-1365.
LI Changyou, XU Minqiang, GAO Jingbo, et al. Rolling bearing fault identification based on ICA[J]. Journal of Harbin Institute of Technology University, 2008, 40(9): 1363-1365. |
 2017, Vol. 49
2017, Vol. 49


