2. 大庆油田采油工程研究院,黑龙江 大庆 163000;
3. 哈尔滨工业大学 电气工程及自动化学院,哈尔滨 150001
2. Research Institute of Oil Production Engineering Daqing Oilfield Company, Daqing 163000, Heilongjiang, China;
3. Institute of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
随着潜油直线电机技术的发展[1],人们提出了一种新型的无杆式抽油装置——潜油柱塞泵.潜油柱塞泵采用井下的潜油直线电机直接驱动柱塞泵柱塞做往复运动,解决了传统游梁式抽油机具有的偏磨严重、体积庞大、造价高以及能耗高等问题,具有良好的应用前景.
潜油柱塞泵采用的结构是倒置方式,即柱塞泵倒置于潜油直线电机之上[2].电机的定子固定在油井底部,动子通过柱塞与柱塞泵的游动凡尔相连,柱塞泵与油管相连,直线电机通过电缆与地面上的控制系统相连.潜油柱塞泵工作时,直线电机的动子做往复运动,带动游动凡尔,不断将套管内液体吸入泵腔内,并将其通过油管举升至地面井口处.但由于油井下的工作环境恶劣,潜油柱塞泵在运行的过程中很容易出现结蜡、砂卡、凡尔漏失、液体充不满等故障现象.如果不对这些故障进行及时的诊断和处理,将会降低潜油柱塞泵工作时的可靠性和寿命.
这种新型无杆式抽油机不同于游梁式抽油机,无法采用传统地面示功图的方法对其进行故障工况诊断.目前,人们虽然已经做了较多的研究并取得了一些成果,但对此还没有提出相对完善的解决方案.针对潜油柱塞泵的故障工况特点,多采用普通遗传算法和粒子群算法[3-6]结合神经网络[7-10]进行故障诊断.粒子群算法适合求解实数问题,但对于离散优化问题处理不佳,容易陷入局部最优.普通遗传算法存在过早收敛和易陷入局部最优等问题[11-12].本文根据采油系统和潜油柱塞泵的结构特点,对油井的载荷、电参数以及井口的油压、套压和温度等数据进行分析,得出数据值与油井故障工况之间的对应关系,提出了适合潜油柱塞泵的MMAGA-RBF故障诊断方法:从系统中提取出用于故障诊断的特征参数;并采用多变异位自适应遗传算法(MMAGA)优化改进型RBF神经网络的权值阈值,采用最优参数的故障诊断模型进行故障诊断.模拟和仿真分析结果表明,该故障诊断方法适用于潜油柱塞泵的多故障工况诊断,并能够达到较高的准确率和可靠性.
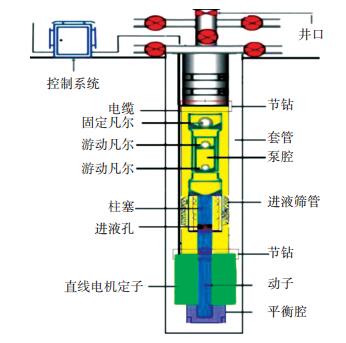
1 特征参数提取由于潜油柱塞泵的柱塞与直线电机的动子直接相连,直线电机的工作状态能够直接反映潜油柱塞泵的运行状态,潜油柱塞泵抽油系统的工作原理图如图 1所示.
|
图 1 潜油柱塞泵原理图 Figure 1 Schematic of submersible plunger pump |
潜油柱塞泵在不同的故障工况下工作时,直线电机的电流和油泵的载荷值是不同的[13-14].比如当潜油柱塞泵出现结蜡、砂卡以及气体影响等故障状态时,直线电机的运行电流便会发生明显的变化.不同故障工况下直线电机的运行电流如图 2所示.

|
图 2 管式直线电机的运行电流曲线 Figure 2 Current curves of tubular linear motor |
虽然对于结蜡、砂卡以及气体影响等常规故障,仅仅依据电流、电功率以及载荷这些特征参数便可以进行故障工况的诊断.但油井的故障工况情况比较复杂,比如有时油井会出现油管漏失,泵阀常开或者电机遇到强烈的机械震动和冲击等问题.此时,只依据上述特征参数便无法准确地进行故障工况诊断.因此,必须通过增加与潜油柱塞泵运行故障工况相关的其他特征参数进行综合分析判定.
在油井正常运行过程中,油井井口的油压和套压是相对稳定的.当出现油管漏失或泵漏失时,油井井口的油压和套压便会发生相应的变化.因此,通过油压表的数值变化,可以帮助人们进一步判定油井的故障工况状态.此外,因油井的井口温度随出油量的大小而相应变化,故井口温度对油井故障工况的判定也是一个很重要的特征参数.本文采用多元数据的方法进行特征参数提取,可以更加真实的反映潜油柱塞泵的故障工况状态,提高故障诊断的准确率.
通过电流和压力传感器等测量装置,对直线电机进行实时监测,并获取电机每个运行周期内相应的电流值以及油泵的载荷.同时记录油井的井口油压和套压以及温度值.
对采集的油井数据值分别作如下处理:
| $ {T_{\rm{e}}} = \frac{1}{l}\sum\limits_{k = 1}^l {T\left( t \right)} . $ | (1) |
式中:l为一个周期内的采样点数,T(t)为实时井口温度,Te为一个周期的平均井口温度.
| $ {F_{{\rm{oe}}}} = \frac{1}{l}\sum\limits_{k = 1}^l {{F_{\rm{o}}}\left( t \right)} . $ | (2) |
式中Fo(t),Foe分别为实时井口油压和一个周期的平均井口油压.
| $ {F_{{\rm{ce}}}} = \frac{1}{l}\sum\limits_{k = 1}^l {{F_{\rm{c}}}\left( t \right)} . $ | (3) |
式中Fc(t),Fce分别为实时井口套压和一个周期的平均井口套压.
| $ {I_{{\rm{ue}}}} = \frac{1}{m}\sum\limits_{k = 1}^m {{i_{\rm{u}}}\left( t \right)} , $ | (4) |
| $ {I_{{\rm{de}}}} = \frac{1}{n}\sum\limits_{k = 1}^m {{i_{\rm{d}}}\left( t \right)} . $ | (5) |
式中:Iue,iu(t),m分别为电机上行程的平均电流、实时电流和采样点数;Ide,id(t),n分别为电机下行程的平均电流、实时电流和采样点数.
| $ {I_{{\rm{uv}}}} = \frac{1}{m}\sum\limits_{k = 1}^m {{{\left( {{i_{\rm{u}}}\left( t \right) - {I_{{\rm{ue}}}}} \right)}^2}} , $ | (6) |
| $ {I_{{\rm{dv}}}} = \frac{1}{n}\sum\limits_{k = 1}^n {{{\left( {{i_{\rm{d}}}\left( t \right) - {I_{{\rm{de}}}}} \right)}^2}} . $ | (7) |
式中Iuv,Idv分别为电机上行程的电流方差和下行程的电流方差.
| $ {P_{{\rm{ue}}}} = \frac{1}{m}\sum\limits_{k = 1}^m {{p_{\rm{u}}}\left( t \right)} , $ | (8) |
| $ {P_{{\rm{de}}}} = \frac{1}{n}\sum\limits_{k = 1}^n {{p_{\rm{d}}}\left( t \right)} . $ | (9) |
式中:Pue,pu(t)分别为电机上行程的平均载荷,实时载荷;Pde,pd(t)分别为电机下行程的平均载荷,实时载荷.
| $ {P_{{\rm{uv}}}} = \frac{1}{m}\sum\limits_{k = 1}^m {{{\left( {{p_{\rm{u}}}\left( t \right) - {P_{{\rm{ue}}}}} \right)}^2}} , $ | (10) |
| $ {P_{{\rm{dv}}}} = \frac{1}{n}\sum\limits_{k = 1}^n {{{\left( {{p_{\rm{d}}}\left( t \right) - {P_{{\rm{de}}}}} \right)}^2}} . $ | (11) |
式中Puv,Pdv分别为电机上行程的载荷方差和下行程的载荷方差.
得到数据Te,Foe,Fce,Iue,Ide,Iuv,Idv,Pue,Pde,Puv,Pdv之后,需要对其进行归一化处理.
| $ \bar x = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}. $ | (12) |
式中:x为归一化后特征参数值;x为归一化前数据实际值;xmax为是各数据序列中的最大值;xmin为是各数据序列中的最小值.
利用式(12)归一化后,得到诊断模型输入向量X=[Te, Foe, Fce, Iue, Ide, Iuv, Idv, Pue, Pde, Puv, Pdv],使得网络的输入值均处于[0, 1]中,有利于神经网络的权值阈值调整进入误差曲面的平坦区.
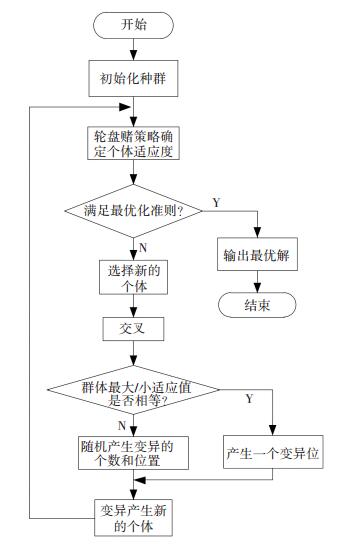
2 MMAGA算法和核函数的选取 2.1 MMAGA算法自适应遗传算法(AGA)[15]是一种具有全局寻优能力的优化算法.它主要包括选择、重组和变异3个操作过程.其中重组概率Pc决定着新个体产生的速度和搜索过程的快慢,而变异概率Pm决定是否产生新的模式.在寻优的过程中,Pc和Pm的取值过大或者过小都会降低遗传算法的寻优能力.因此,必须选取合适的Pc和Pm,以保证得出最优解.而多变异位遗传算法[16-17]是在自适应遗传算法中引入多位变异,根据个体的优劣情况决定其变异位数,即适应度低的个体变异多个基因,而适应度高的个体进行少位变异甚至不变异,由此可形成多种变异组合,进一步增大最优解的搜索空间,其算法流程图如图 3所示.该算法中的Pc和Pm的取值分别由以下公式计算.
|
图 3 MMAGA算法流程图 Figure 3 Flow chart of MMAGA |
| $ {p_{\rm{c}}} = \left\{ {\begin{array}{*{20}{c}} {{p_{{\rm{c}}1}} \times \frac{{\hat f - {f_{\rm{e}}}}}{{{f_{\max }} - {f_{\rm{e}}}}},}&{\hat f \ge {f_{\rm{e}}};}\\ {{p_{{\rm{c}}2}},}&{\hat f < {f_{\rm{e}}}.} \end{array}} \right. $ | (13) |
| $ {p_{\rm{m}}} = \left\{ {\begin{array}{*{20}{c}} {{p_{{\rm{m}}1}} \times \frac{{f - {f_{\rm{e}}}}}{{{f_{\max }} - {f_{\rm{e}}}}},}&{f \ge {f_{\rm{e}}};}\\ {{p_{{\rm{m}}2}},}&{f < {f_{\rm{e}}}.} \end{array}} \right. $ | (14) |
式中:fmax为群体最大适应值;fe为群体平均适应值;
较常用的神经网络有BP神经网络[18-20]和标准径向基神经网络[21-22]. BP算法的收敛速度慢,网络的容错能力差,易陷入局部最优解.而RBF算法的输入和输出之间具有较强的映射性,收敛速度快和分类能力好.但传统高斯核函数具有一定的缺陷,比如在数据中心点附近的衰减速度相对较慢,在远离中心点处,由于函数值会不断地趋于零,最终会造成核截断现象.这在一定程度上影响神经网络的分类能力和准确率.为进一步提高其收敛性和分类能力,改善模型的诊断能力和准确率,本文选用改进型高斯核函数作为网络的核函数.
本文选用的神经网络传递函数形式为
| $ {u_i} = \exp \left( {\frac{{\sigma _i^2}}{{{{\left\| {x - {c_i}} \right\|}^2} + {\xi ^2}}}} \right). $ | (15) |
式中:ui, ci, σi, ξ分别为隐含层节点i的输出、高斯核函数的中心、核宽带变量和位移参数.
从图 4中可以看出,改进型高斯核函数比传统高斯核函数在中心点处的衰减性能更佳,同时远离中心时的衰减速度又相对较慢且趋于某一非零常数.改进型高斯核函数可以有效地避免传统高斯核函数的缺陷,提高神经网络的诊断能力和准确率.

|
图 4 两种核函数的特性比较 Figure 4 Curves of RBF and modified RBF |
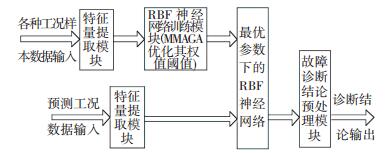
潜油柱塞泵的常见故障工况有油管结蜡S1、供液不足S2、气体影响S3、砂卡S4、凡尔漏失S5和泵抽空S6等类别,本文仅对以上6种常见故障工况进行研究与分析. MMAGA-RBF故障诊断模型的结构图如图 5所示.首先采集以上各种故障工况下实际生产过程中的潜油直线电机的运行电流i、载荷p和井口的油压Fo、套压Fc以及井口处的温度T等运行参数,并提取出特征参数,得到相应故障工况下的输入向量即训练样本数据;然后在离线状态下利用这些故障工况的训练样本数据对RBF神经网络进行反复训练,同时利用MMAGA优化RBF神经网络的权值阈值,获得RBF神经网络的最优权值阈值;最终利用最优参数下的RBF神经网络诊断模型实现在线实时诊断,并输出故障诊断结果.此外,根据训练样本数据的维数及故障诊断模型待辨识的故障类型个数,选定RBF神经网络的输入层节点数为11,输出层节点数为6,隐含层节点数的具体确定方法则在实验分析过程中进一步阐述.假如潜油柱塞泵的故障工况诊断结果为砂卡S4,则RBF神经网络输出层的对应期望结果为{0 0 0 1 0 0}.
|
图 5 故障诊断模型结构图 Figure 5 The structure of fault diagnosis model |
由于RBF神经网络具有容易陷入局部最优和收敛速度慢的特点[23-24],而MMAGA的全局寻优能力较强.因此,本文采用MMAGA算法优化RBF神经网络的权值阈值,种群中的每个个体都包含了一个网络的所有权值阈值,通过选择、重组和变异操作,使之达到最优的取值,提高故障诊断模型的准确率.
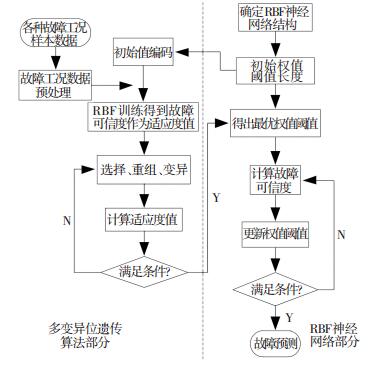
实验中对油井的油管结蜡、供液不足、气体影响、砂卡、凡尔漏失和泵抽空等故障工况各采集300组工况数据作为训练样本集,经数据预处理后获取相应故障工况的输入向量;首先确定神经网络的结构,初始化MMAGA中的变量个数NIND、最大遗传代数Maxgen、变异概率和重组概率等参数值,并创建初始种群;利用训练样本集对初始化参数的RBF神经网络进行离线训练,将得出的故障可信度作为适应度值;根据轮盘赌策略确定父代,对父代进行自适应重组和变异操作,产生新的个体,并计算子代适应度值;判断此时是否达到要求的故障诊断准确率,若满足要求,便得到最优的权值阈值,否则,继续进行上述的选择、重组和变异操作;然后继续采用梯度下降法进一步更新其权值阈值,直至故障可信度满足终止条件,最终得出RBF神经网络用于在线实时故障预测的最优参数. MMAGA-RBF故障诊断方法的流程图如图 6所示.
|
图 6 MMAGA算法优化RBF神经网络流程图 Figure 6 Flow chart of MMAGA optimizing RBFNN |
实验中使用油井模拟循环系统来模拟潜油柱塞泵的各种故障工况进行实验分析,该实验平台主要由油井模拟循环系统、流量控制装置、潜油柱塞泵及其控制装置组成,实验平台的实物图如图 7所示.

|
图 7 实验平台实物 Figure 7 Experiment platform |
在实验平台上分别模拟潜油柱塞泵在油管结蜡、供液不足、气体影响、砂卡、凡尔漏失及泵抽空等6种常见故障工况下的工作状态,并对其故障工况数据进行采集.本文中使用压力传感器和电流传感器来采集潜油柱塞泵各种故障工况下井下的工作数据,井下数据采集设备采集器如图 8所示.此外,通过井口处的油压表、套压表和温度表获取各种故障工况下相应的工况数据.

|
图 8 井下设备实物图 Figure 8 The downhole equipment |
实验中,为了使获取的数据更加具有代表性和研究性,分别对同一故障工况下的不同时间段进行数据采集作为训练样本集和测试样本集.因此,先在模拟实验平台上模拟油管结蜡S1、供液不足S2、气体影响S3、砂卡S4、凡尔漏失S5和泵抽空S6等6种常见故障工况分别采集300组运行数据,作为训练样本集,再次重复模拟上述6种故障工况采集100组新的运行数据,作为测试样本集.因实验条件的限制,在实际的实验分析过程中,本文提出的故障诊断模型的训练过程和测试验证过程均是在离线模式下进行的.
因RBF神经网络的诊断效果不仅与其权值阈值有关,还与隐含层的节点数有关.为了选择合适的隐含层节点数,从上述故障工况采集的训练样本集中抽取1 200组工况数据(油管结蜡S1、供液不足S2、气体影响S3、砂卡S4、凡尔漏失S5和泵抽空S6等故障工况各200组)作为训练样本,对RBF神经网络进行反复训练,并利用上述测试样本集对其故障诊断准确率进行验证,从而找到隐含层节点数的最佳取值.
在确定故障诊断模型的最佳参数之后,进一步研究MMAGA-RBF故障诊断方法的泛化性能.从上述故障工况采集的训练样本集中从小到大依次抽取不同数量(200~1 200组)的训练样本,先利用训练样本对MMAGA-RBF故障诊断模型进行反复训练,然后利用上述100组测试样本集对其故障诊断准确率的性能进行验证分析.
4.2 仿真实验结果分析实验仿真结果表明,MMAGA-RBF故障诊断方法的诊断准确率不仅与故障诊断模型的参数有关,还与训练该故障诊断模型的训练样本数量相关.具体实验分析过程如下.
首先使用较少的训练样本来分析模型的泛化性能.此处从训练样本集中随机抽取360组(油管结蜡S1、供液不足S2、气体影响S3、砂卡S4、凡尔漏失S5和泵抽空S6等故障工况各60组数据)数据做训练样本,对故障诊断模型进行反复训练之后,统计其对100组测试样本集诊断的准确率.由于训练的数据较少,所以只有增加训练次数,才能使提高故障诊断的准确率. 图 9为不同最大迭代次数下100组测试样本集的综合诊断准确率结果.

|
图 9 诊断准确率变化曲线 Figure 9 Curve of judgment rate |
从图 9的结果中可知,当训练样本数量较少时,故障诊断准确率相对较低.在初始阶段,故障诊断准确率随着最大迭代次数的增加而提高,但是当最大迭代次数增大到一定值时,其趋势逐渐变得缓慢,基本上停止改善,保持稳定状态,出现过拟合现象.
通过增加训练样本数量可有效防止过拟合现象的发生,提高故障模型的诊断准确率.实验中分别选择200~1 200组各种故障工况下的训练样本数据,测试在不同训练样本数量和最大迭代次数下的综合诊断误判率.具体仿真结果如图 10所示.

|
图 10 测试数据误判率仿真结果 Figure 10 Misjudgment rates of test data |
从结果中可知,当训练样本的数量增加时,故障诊断的综合误判率会明显降低.在训练样本数量达到1 000组以上时,该故障诊断方法的误判率可控制在4%以内,具有较高的综合故障诊断能力.其中,砂卡和结蜡容易出现误判现象,其余类型的故障工况基本能够准确诊断.
最后,将MMAGA-RBF故障诊断方法与标准GA-RBF故障诊断方法进行对比分析.在不同的训练样本下,二者的诊断准确率曲线如图 11所示.当训练样本数量较少时,两种故障诊断方法的综合诊断准确率都比较低.但随着训练样本数量的增加,MMAGA-RBF故障诊断方法的准确率明显比GA-RBF故障诊断方法的准确率高一些.虽然随着样本数量的增加GA-RBF故障诊断准确率能够继续增加,但由于获取大量训练样本的成本较高,会造成很大的工作量.因此,期望通过获取庞大的训练样本来提高其诊断能力,不是一个可行的方案.

|
图 11 两种故障诊断方法的诊断准确率曲线 Figure 11 Diagnostic accuracy curves of the two fault diagnosis methods |
由于本文提出的MMAGA-RBF故障诊断方法在离线状态下通过充足的训练样本进行反复训练得到最佳的参数之后不必再次重复训练,在实际的故障诊断应用中,只需要将潜油柱塞泵的待测故障数据经过预处理之后,直接进行故障诊断即可.因此,该故障诊断方法可以实现潜油柱塞泵运行工况的在线实时诊断.
5 结论1) 随着训练样本数量的增加,MMAGA-RBF故障诊断模型的诊断准确率不断提高,在训练样本数量为1 000组时,综合诊断准确率便可达到96%以上.这表明该故障诊断方法可在相对较少的训练样本下达到很高的诊断准确率.相比于其他故障诊断方法,大大地减少了成本与工作量.
2) 该故障诊断方法能够避免传统径向基核函数的缺陷,改善其收敛性和分类能力,达到更高的诊断准确率;
3) 该故障诊断方法的泛化能力强,能满足实验中潜油柱塞泵井下常见故障工况类别的准确判定,预测故障的发生,并及时进行处理,提高潜油柱塞泵的工作可靠性.
4) 由于实验条件的限制,在实验中只对潜油柱塞泵的上述6种常见故障工况进行了仿真分析.根据实验中现有的故障数据,MMAGA-RBF故障诊断方法能够达到其综合诊断准确率的要求.至于该故障诊断方法对所有故障类型的诊断效果,则需要模拟仿真更全面的故障类别以获取更多的故障工况数据来训练故障诊断模型,进一步研究该方法的有效性.
| [1] |
陈梁远, 李黎川. 压缩机用直线电机及其关键技术发展综述[J].
中国电机工程学报, 2013, 33(15): 52-68.
CHEN Liangyuan, LI Lichuan. Development of the linear motor and its key technologies for compressors[J]. Proceedings of the CSEE, 2013, 33(15): 52-68. |
| [2] |
于德亮, 邓盛川, 张永明, 等. 基于支持向量机的潜油往复式油田抽油机故障工况诊断方法[J].
电工技术学报, 2013, 28(4): 248-254.
YU Deliang, DENG Shengchuan, ZHANG Yongming, et al. Working condition diagnosis method based on SVM of submersible plunger pump[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 248-254. |
| [3] |
BENMOUIZA K, TADJ M, CHEKNANE A. Classification of hourly solar radiation using fuzzy c-means algorithm for optimal stand-alone PV system sizing[J].
International Journal of Electrical Power & Energy Systems, 2016, 82: 233-241.
|
| [4] |
OZYILDIRIM B M, AVCI M. One pass learning for generalized classifier neuralnetwork[J].
Neural Networks, 2016, 73: 70-76.
DOI: 10.1016/j.neunet.2015.10.008 |
| [5] |
LI X, ZECCHIN A C, MAIER H R. Selection of smoothing parameter estimators for general regression neural networks-applications to hydrological and water resourcesmodelling[J].
Environmental Modelling & Software, 2014, 59: 162-186.
|
| [6] |
陈智慧. 基于JADE平台的粒子群算法在经济调度中的应用[J].
电气技术, 2015, 16(1): 32-35.
CHEN Zhihui. The particle swarm algorithm based on JADE platform application in the economic operation[J]. Electric technology, 2015, 16(1): 32-35. |
| [7] |
PARK I M, SETH S, PAIVA A, et al. Kernel methods on spike train space for neuroscience: a tutorial[J].
IEEE Signal Processing Magazine, 2013, 30(4): 149-160.
DOI: 10.1109/MSP.2013.2251072 |
| [8] |
IJJINA E P, MOHAN C K. Hybrid deep neural network model for human actionrecognition[J].
Applied Soft Computing Journal, 2016, 46: 936-952.
DOI: 10.1016/j.asoc.2015.08.025 |
| [9] |
KIM J S, JUNG S. Implementation of the RBF neural chip with the back-propagation algorithm for on-line learning[J].
Applied Soft Computing, 2015, 29: 233-244.
DOI: 10.1016/j.asoc.2014.12.018 |
| [10] |
谢东, 张兴, 曹仁贤. 基于小波变换与神经网络的孤岛检测技术[J].
中国电机工程学报, 2014, 34(4): 537-544.
XIE Dong, ZHANG Xing, CAO Renxian. Islanding detection based on wavelet transform and neural network[J]. Proceedings of the CSEE, 2014, 34(4): 537-544. |
| [11] |
颜晓娟, 龚仁喜, 张千锋. 优化遗传算法寻优的SVM在短期风速预测中的应用[J].
电力系统保护与控制, 2016, 44(9): 38-42.
YAN Xiaojuan, GONG Renxi, ZHANG Qianfeng. Application of optimization SVM based on improvedgenetic algorithm in short-term wind speed prediction[J]. Power System Protection and Control, 2016, 44(9): 38-42. DOI: 10.7667/PSPC150294 |
| [12] |
刘柏良, 黄学良, 李军. 计及可时移负荷的海岛微网电源优化配置[J].
中国电机工程学报, 2014, 34(25): 4250-4258.
LIU Bailiang, HUANG Xueliang, LI Jun. Optimal sizing of distributed generation in a typical island microgrid with time-shifting load[J]. Proceedings of the CSEE, 2014, 34(25): 4250-4258. |
| [13] |
李立毅, 唐勇斌, 刘家曦, 等. 多种群遗传算法在无铁心永磁直线同步电机优化设计中的应用[J].
中国电机工程学报, 2013, 33(15): 69-77.
LI Liyi, TANG Yongbin, LIU Jiaxi, et al. Application of the multiple population genetic algorithm in optimum design of air-core permanent magnet linear synchronous motors[J]. Proceedings of the CSEE, 2013, 33(15): 69-77. |
| [14] |
王博, 赵海森, 李和明, 等. 用于模拟游梁式抽油机电动机动态负荷的测试系统设计及应用[J].
中国电机工程学报, 2014, 34(21): 3488-3495.
WANG Bo, ZHAO Haisen, LI Heming, et al. Design and applications of the testing system with dynamic load for beam pumping motor[J]. Proceedings of the CSEE, 2014, 34(21): 3488-3495. |
| [15] |
WANG D. Sensitivity analysis of structural response to position of external applied load: in plane stress condition[J].
Structural and Multidisciplinary Optimization, 2014, 50(4): 605-622.
DOI: 10.1007/s00158-014-1075-1 |
| [16] |
HERIS J E A, OSKOEI M A. Modified genetic algorithm for solving n-queens problem[C]//2014 Iranian Conference on Intelligent Systems. Bam, Iran: IEEE Press, 2014:1-5.
http://ieeexplore.ieee.org/document/6802550/
|
| [17] |
龚纯, 王正林.
精通MATLAB最优化计算[M]. 3版. 北京: 电子工业出版社, 2014: 337-341.
GONG Chun, WANG Zhenglin. Proficient in MATLAB optimization[M]. 3rd ed. Beijing: Electronic Industry Press, 2014: 337-341. |
| [18] |
李龙, 魏靖, 黎灿兵, 等. 基于人工神经网络的负荷模型预测[J].
电工技术学报, 2015, 30(8): 225-230.
LI Long, WEI Jing, LI Canbing, et al. Prediction of load model based on artificial neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 225-230. |
| [19] |
郭孜政, 谭永刚, 马国忠, 等. 基于BP神经网络的驾驶精神疲劳识别方法[J].
哈尔滨工业大学学报, 2014, 46(8): 18-121.
GUO Zizheng, TAN Yonggang, MA Guozhong, et al. Recognition method of driving mental fatigue based on BP neural network[J]. Journal of Harbin Institute of Technology, 2014, 46(8): 18-121. DOI: 10.11918/j.issn.0367-6234.2014.08.020 |
| [20] |
龙亿, 杜志江, 王伟东. GA优化的RBF神经网络外骨骼灵敏度放大控制[J].
哈尔滨工业大学学报, 2015, 47(7): 26-30.
LONG Yi, DU Zhijiang, WANG Weidong. RBF neural network with genetic algorithm optimization based sensitivity amplification control for exoskeleton[J]. Journal of Harbin Institute of Technology, 2015, 47(7): 26-30. DOI: 10.11918/j.issn.0367-6234.2015.07.003 |
| [21] |
GUAN X, ZHU Y, SONG W. Application of RBF neural network improved by peak density function in intelligent color matching of wooddyeing[J].
Chaos, Solitons & Fractals, 2016, 89: 485-490.
|
| [22] |
YU Deliang, ZHANG Yongming. A new diagnostic method for identifying working conditions of submersible reciprocating pumping systems[J].
Petroleum Science, 2013, 10(1): 81-90.
DOI: 10.1007/s12182-013-0253-x |
| [23] |
LI X, ZHAO L, WEI L, et al. Deep saliency: multi-task deep neural network model for salient object detection[J].
IEEE Transactions on Image Processing, 2015, 25(8): 3919-3930.
|
| [24] |
TANG Y, GAO H, KURTHS J. Multiobjective identification of controlling areas in neuronal networks[J].
IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2013, 10(3): 708-720.
DOI: 10.1109/TCBB.2013.72 |
 2017, Vol. 49
2017, Vol. 49


