热稳定性是当热流波动时围护结构温度保持相对稳定的性能，随着节能建筑轻型化以及装配式建筑和被动式建筑等新技术的发展，建筑热稳定设计及其对室内热环境和建筑能耗影响的定量评价问题日益凸显.

围护结构热稳定性能计算是进行室内空气温度波动分析、建筑能耗分析及隔热/蓄热模型优化的基础^[1-2].基于谐波分析法的建筑热稳定理论模型，能够解决围护结构对室内或室外扰量的热响应特性关键问题，反映热流波动周期、围护结构热工参数等因素对非稳态传热过程的影响^[3-4].其对周期性传热过程的描述物理意义清晰、计算过程相对简单，被广泛应用于非稳态建筑热过程的计算.

热惰性指标D是谐波分析法热稳定理论模型中的关键参数^[5-8]，对内表面蓄热系数、衰减倍数及延迟时间等参数的计算都具有决定性影响.然而，中国鲜见关于热惰性指标对围护结构热稳定性能作用机制的研究，尤其欠缺关于热惰性指标物理意义的确切解释.GB50176-93《民用建筑热工设计规范》^[9]指出：“有些名词要给出一个确切的定义十分困难，这里只能给出一个近似的名词解释，如蓄热系数、热惰性指标、热稳定性等”，其中热惰性指标的术语解释为“表征围护结构对温度波衰减快慢程度的量纲一的指标”.而现行GB50176-2016《民用建筑热工设计规范》^[10]中关于热惰性指标的术语修改为：“热惰性表征受到波动热作用时，材料层抵抗温度波动的能力，用热惰性指标D来描述，其表现为背波面温度波动的大小”.这些术语定性描述了热惰性指标的影响结果，却不能解释热惰性指标为何起到这样的作用.

鉴于此，本文通过理论推导和数值模拟分析，给出热惰性指标与温度波及热流波衰减的函数关系式，揭示热惰性指标对围护结构内温度波动的影响机制，分析其对相关热工参数计算的关键作用，为中国关于热惰性指标的物理意义由定性描述改进为定量描述提供了理论依据.

1 围护结构中温度波衰减问题求解及热惰性指标D的作用 1.1 围护结构中温度波模型及解析解

在计算机模拟技术发达的条件下，即便可以用软件解决围护结构非稳态传热复杂问题计算，但是对其数理模型中参数作用机制的深入理解，有助于更好地发展优化热稳定性能.

围护结构中的非稳态传热在材料各向同性条件下满足傅里叶导热微分方程：

$ \frac{{\partial t\left( {x,\tau } \right)}}{{\partial \tau }} = a\frac{{{\partial ^2}t\left( {x,\tau } \right)}}{{\partial {x^2}}}. $

(1)

式中：t(x, τ)为围护结构各时刻各位置的温度，℃；τ为时刻，s；a为围护结构材料的导温系数，m²/s；x为距围护结构表面的距离，m.

为了计算出整个围护结构内及其表面上温度波动的衰减，需求解出任意时刻τ和任意截面x处的温度t(x, τ).已有研究表明^[11]，对于温度波在围护结构中的衰减问题，简便方法是采用同时具有双曲函数和复变函数形式的解.

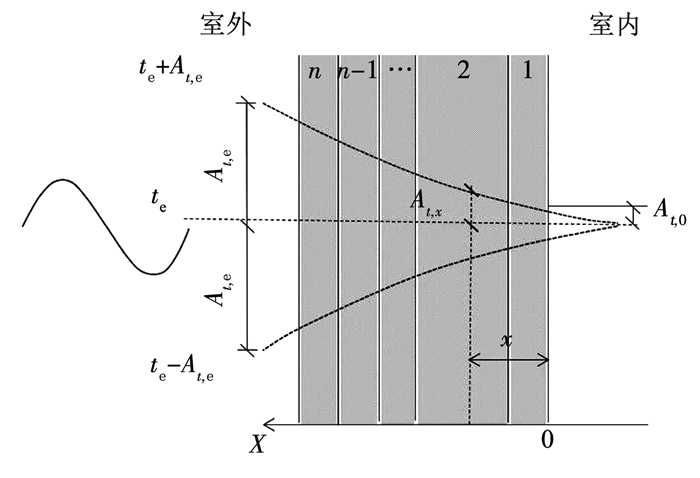
以室外空气通过围护结构向室内传热为例，由于衰减倍数和延迟时间均以围护结构内表面作为参照面，同时考虑计算简便，令围护结构内表面处x=0，如图 1所示.

由于室外气象参数呈周期性变化，所以围护结构的边界条件为周期性温度波，根据分离变量法^[12]，求解式(1)可得

$ \dot t\left( {x,\tau } \right) = {{\rm{e}}^{\frac{{2{\rm{ \mathsf{ π} }}\tau {\rm{i}}}}{T}}}\left( {{A_{t,0}}{\rm{ch}}\sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}} x + \frac{{{A_{q,0}}}}{{S\sqrt {\rm{i}} }}{\rm{sh}}\sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}x} } \right). $

(2)

式中: $ \dot t(x, \tau ) $为围护结构各时刻各位置温度的复数形式，℃；A_{t, 0}为围护结构内表面温度振幅，℃；A_{q, 0}为围护结构内表面热流振幅，W/m²；T为温度波周期，h；S为材料的蓄热系数，W/(m²·℃)，$ S = \sqrt {\frac{{2{\rm{\pi }}\lambda \rho c}}{T}} $, 其他符号意义同前.

在式(2)中，$ {{\rm{e}}^{\frac{{2{\rm{ \mathsf{ π} }}\tau {\rm{i}}}}{T}}} $项反映了围护结构τ时刻对应的温度波相位因子，其模恒等于1，只改变幅角(相位角)，对温度振幅的大小没有影响.因此，距离内表面x处的温度波振幅的复数形式为

$ {{\dot A}_{t,x}} = {A_{t,0}}{\rm{ch}}\sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}} x + \frac{{{A_{q,0}}}}{{S\sqrt {\rm{i}} }}{\rm{sh}}\sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}x} . $

(3)

式中: $ {\dot A_{t, x}} $为距内表面x处的温度波振幅，℃; 同理，根据傅里叶定律$q = - \lambda \frac{{\partial t}}{{\partial x}} $，可以求得围护结构内热流密度波动振幅的复数形式为

$ {{\dot A}_{q,x}} = \lambda \sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}} \left( {{A_{t,0}}{\rm{sh}}\sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}} x + \frac{{{A_{q,0}}}}{{S\sqrt {\rm{i}} }}{\rm{ch}}\sqrt {\frac{{2{\rm{ \mathsf{ π} i}}}}{{Ta}}} x} \right). $

(4)

式中:${\dot A_{q, x}} $为距内表面x处的热流波振幅，W/m²；λ为导热系数，W/(m·℃), 其他符号意义同前.

对于单一材料围护结构或单一材料层，引入热惰性指标参数为

$ D = RS. $

(5)

式中：D为热惰性指标；R为材料层热阻，m²·℃/W，距内表面x处R_x=x/λ.热惰性指标D是材料蓄热系数S与热阻R组合而成的一个量纲一的参数.将式(5)代入式(3)、(4)可得:

$ {{\dot A}_{t,x}} = {A_{t,0}}{\rm{ch}}{D_x}\sqrt {\rm{i}} + \frac{{{A_{q,0}}}}{{S\sqrt {\rm{i}} }}{\rm{sh}}{D_x}\sqrt {\rm{i}} , $

(6)

$ {{\dot A}_{q,x}} = S\sqrt {\rm{i}} \left( {{A_{t,0}}{\rm{sh}}{D_x}\sqrt {\rm{i}} + \frac{{{A_{q,0}}}}{{S\sqrt {\rm{i}} }}{\rm{ch}}{D_x}\sqrt {\rm{i}} } \right). $

(7)

对比式(3)与式(6)、式(4)与式(7)可见，热惰性指标D以替代x表示所在截面处于材料层中的位置，也被称作“假想厚度”^[13]，是求解温度波以及热流波衰减问题的关键参数.

1.2 D与温度波衰减的关系式

热惰性指标对温度波动衰减的作用可通过数学推导进行揭示.随着温度波的推进，波幅逐渐减小，相位发生延迟，称之为温度波的衰减.由式(6)可得，从距离内壁面x处到内壁面的温度波衰减${\dot \nu _x} $的复数计算式为

$ {{\dot \nu }_x} = \frac{{{{\dot A}_{t,x}}}}{{{A_{t,0}}}} = {\rm{ch}}{D_x}\sqrt {\rm{i}} + \frac{{{A_{q,0}}}}{{{A_{t,0}}S\sqrt {\rm{i}} }}{\rm{sh}}{D_x}\sqrt {\rm{i}} , $

(8)

对式(8)进行双曲函数变换和复数变换可得^[11]

$ {{\dot \nu }_x} = {{\rm{e}}^{{D_x}\sqrt {\rm{i}} }}\frac{{S\sqrt {\rm{i}} + {Y_{\rm{i}}}}}{{S\sqrt {\rm{i}} + {Y_x}}}. $

(9)

式中：Y_i为围护结构内表面蓄热系数，W/(m²·℃)，Y_i=A_{q, 0}/A_{t, 0}；Y_x为表面蓄热系数，表示在距离内壁面x处热流波振幅${\dot A_{q, x}} $与温度波振幅$ {\dot A_{t, x}} $的比值，即${Y_x} = {\dot A_{q, x}}/{\dot A_{t, x}} $.在相同的${\dot A_{q, x}} $下，Y_x越大，则$ {\dot A_{t, x}} $越小，表明x截面热稳定性越强.

对于无限厚(D > 1)单层匀质材料，$ {Y_{\rm{i}}} = {Y_x} = S\sqrt {\rm{i}} $，则式(9)变为

$ {{\dot \nu }_x} = {{\rm{e}}^{{D_x}\sqrt {\rm{i}} }}, $

(10)

式(10)的模为$ {{\rm{e}}^{\frac{{{D_x}}}{{\sqrt 2 }}}} $，表示在x距离内波动幅度的衰减倍数，而幅角为$ \frac{{{D_x}}}{{\sqrt 2 }} $弧度，表示在x距离内初相角的改变，即谐波相位的延迟，可得单层匀质材料构成的围护结构内温度波衰减倍数ν和相位延迟Φ分别为^[13]：

$ \nu = {{\rm{e}}^{\frac{D}{{\sqrt 2 }}}}, $

(11)

$ \mathit{\Phi } = \frac{D}{{\sqrt 2 }}. $

(12)

温度波在单层匀质围护结构内的延迟时间可按下式计算：

$ {\xi _0} = \frac{\mathit{\Phi }}{{2{\rm{ \mathsf{ π} }}}}T = \frac{\mathit{D}}{{2\sqrt 2 {\rm{ \mathsf{ π} }}}}T. $

(13)

可见，当围护结构由单一材料组成时，温度波的衰减倍数ν及延迟时间ξ₀只受热惰性指标D影响，D越大，ν和ξ₀越大，温度波的衰减和延迟越强.

1.3 D与围护结构内温度波数量的关系式

根据式(12)，一定厚度单一材料墙体内温度波的数量n按下式计算：

$ n = \frac{\mathit{\Phi }}{{2{\rm{ \mathsf{ π} }}}} = \frac{\mathit{D}}{{2\sqrt 2 {\rm{ \mathsf{ π} }}}}. $

(14)

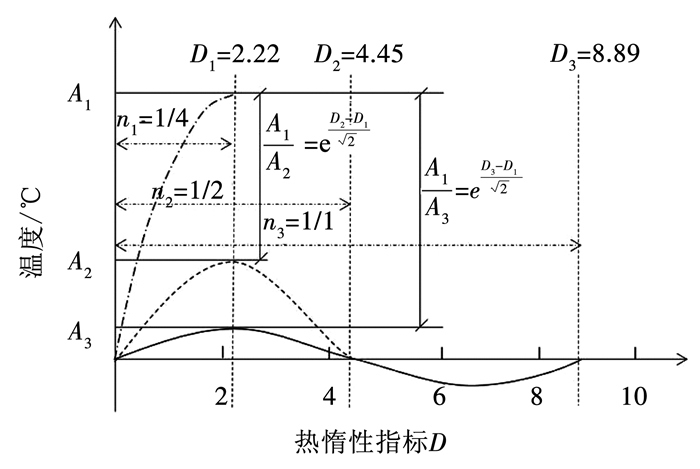
从式(14)可看出，D可以反映围护结构内温度波的数量，如图 2所示.

由图 2可见，D越大，围护结构中分布的温度波数量n越多，温度波幅沿材料层厚度衰减越快.当$ D = 2\sqrt 2 {\rm{ \mathsf{ π} }} \approx 8.9 $时，相位延迟Φ=2π，n=1，即D≈8.9的围护结构内存在一个完整的温度波；而当$ D = \sqrt 2 {\rm{ \mathsf{ π} }} \approx 4.45 $时，则Φ=π，n=1/2，即D≈4.45的围护结构内存在1/2个温度波，以此类推，可以根据D求得围护结构内温度波的数量n.

为进一步分析D对围护结构内温度波数量的影响，以钢筋混凝土墙体和炉渣混凝土墙体为例，计算不同D值下墙体厚度及温度波数量.钢筋混凝土热工参数：ρ=2 500 kg/m³，λ=1.74 W/(m·K)，C=0.92 kJ/(kg·℃)，S₂₄=17.2 W/(m²·℃)，S₁₂=12.16 W/(m²·℃)，S₈=9.93 W/(m²·℃)；炉渣混凝土热工参数：ρ=1 700 kg/m³，λ=1.0 W/(m·W)，C=1.05 kJ/(kg·℃)，S₂₄=11.68 W/(m²·℃)，S₁₂=8.26 W/(m²·℃)，S₈=6.74 W/(m²·℃)，根据式(14)，计算结果见表 1.

由表 1可见，围护结构D值相同时，由于热流波动周期不同、建筑材料不同，对应的围护结构的厚度也不同，但是，围护结构内温度波的数量n相同，即围护结构内温度波的数量只由热惰性指标D决定.

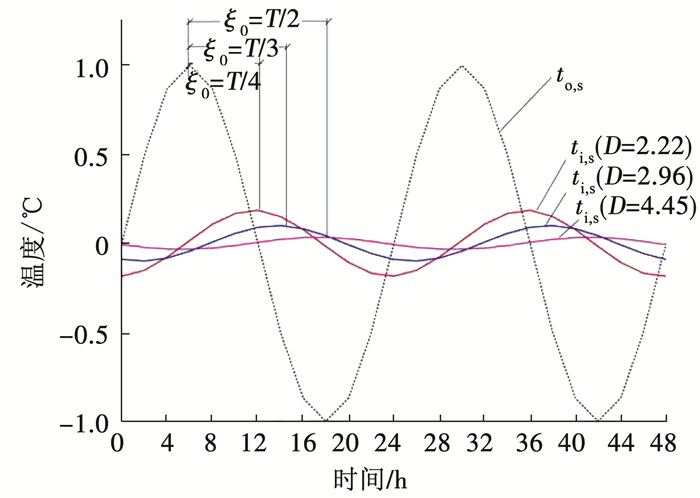
2 D对围护结构内温度波动影响的模拟分析

为了更直观验证热惰性指标与墙体内温度波衰减的关系，本文在墙体外表面温度t_{o, s}周期为T=24 h，振幅为1℃的正弦温度波条件下，通过ANSYS软件对不同热惰性指标钢筋混凝土墙体的内表面温度t_{i, s}进行模拟计算, 模拟结果如图 3所示，显示了不同热惰性指标钢筋混凝土墙体的温度波衰减和延迟规律.

从计算式(11)、(13)可知，D值不同的墙体抵抗温度波动的能力不同，且衰减倍数ν、延迟时间ξ₀与D成正相关关系.由图 3可见，D值愈大，围护结构内温度波延迟时间ξ₀越长，温度波沿材料层厚度衰减倍数ν越大.

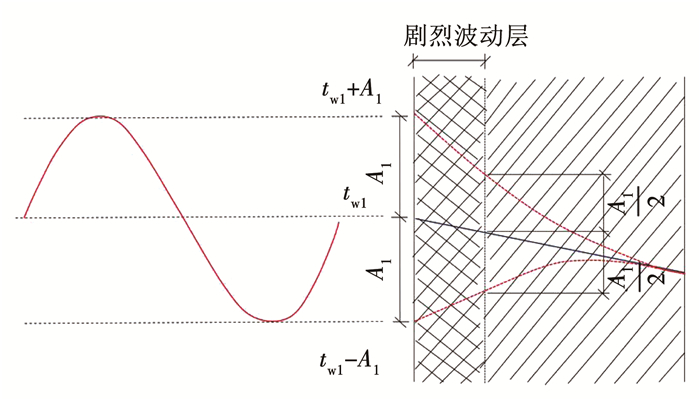
3 D对相关热稳定性能参数计算的关键影响 3.1 剧烈波动层厚度的计算

沿温度波传递方向，围护结构内温度的波幅不断衰减.如图 4所示，定义温度波幅衰减为表面温度波幅1/2处的围护结构层为“温度剧烈波动层^[13]”，其厚度为“剧烈波动层厚度”.

剧烈波动层厚度在建筑蓄热设计中具有重要意义，根据Q=mCΔt，由于温度波动幅度大，热量大部分储存在温度剧烈波动层内.而在温度剧烈波动层之外的围护结构部分，由于温度波幅小，对蓄热的作用相对不大.因此，可将温度剧烈波动层厚度认为“有效蓄热层厚度”.

温度剧烈波动层厚度的计算取决于D值.根据式(11)，剧烈波动层边界处的温度波幅衰减倍数$ \nu = {{\rm{e}}^{\frac{D}{{\sqrt 2 }}}} = 2 $，则剧烈波动层的热惰性指标D_δ=1.

$ {D_\delta } = {R_\delta }S = \frac{\delta }{\lambda }S = 1. $

式中:δ为剧烈波动层厚度，m；R_δ为剧烈波动层的热阻，m²·℃/W；S为剧烈波动层材料的蓄热系数，W/(m²·℃)；其他符号意义同前.

剧烈波动层厚度δ按下式计算：

$ \delta = \frac{\lambda }{S} = \sqrt {\frac{T}{{2{\rm{ \mathsf{ π} }}}}\frac{\lambda }{{\rho c}}} , $

式中:符号意义同上.

热惰性指标D以及剧烈波动层厚度δ，都与热流的波动周期T有关.傅里叶级数将热作用展开成若干个不同阶数的谐波热作用之和，一阶、二阶、三阶波对应的波动周期分别为24、12、8 h.本文选取几种常见蓄热材料，计算不同温度波动周期时相应的δ值，结果见表 2.

由表 2可知，波动周期越大，剧烈波动层厚度δ越大，反之δ小.一阶波作用下，常用建筑材料的有效蓄热厚度约为8~10 cm；对于间歇供暖或制冷的房间，若热源波动为二阶和三阶波，则有效蓄热层厚度也随之减小.

剧烈波动层厚度概念及其计算方法，不仅对其他关键热稳定性能参数，如内表面蓄热系数、衰减倍数和延迟时间具有决定性的影响，而且为围护结构有效蓄热设计方法提供了新的思路.

3.2 内表面蓄热系数计算边界的确定

内表面蓄热系数Y_i被定义为围护结构内表面热流波动振幅A_q与温度波动振幅A_t的比值，是表征围护结构表面蓄热能力的重要参数.

根据“温度剧烈波动层”的物理意义，认为Y_i只与剧烈波动层内材料热工特性有关，剧烈变化层之外的部分，则对Y_i不产生影响^[11].Y_i计算方法见表 3，从围护结构内侧向外侧逐层推算.因为剧烈波动层厚度内材料的热惰性指标D=1，所以，在计算Y_i时，首先以材料层D≥1、D＜1为判断标准，确定剧烈波动层边界在多层围护结构中的位置，然后，只在D=1的剧烈波动层内计算Y_i.因此，整个围护结构的D值大，Y_i不一定大.

如果整个围护结构D＜1，说明剧烈波动层边界落在该围护结构之外，整个围护结构处于剧烈波动层内，所以计算Y_i时，需要从最外层开始计算.

在中国相关资料^{[9, 14]}中关于Y_i规定“每一层围护结构均D＜1时，则从最外层开始计算”.根据上述温度剧烈波动层理论，如果墙体每一层均D＜1，而前n层材料的总热惰性指标D≥1时，则应从第n层开始计算Y_i.内表面蓄热系数Y_i的计算主要与剧烈波动层厚度内材料热工参数有关，可以解释采用D=1作为Y_i计算边界的依据.

3.3 D对多层围护结构热稳定性的影响

由多层匀质材料层组成的围护结构的热惰性指标按下式计算.对于多层围护结构，材料层排列顺序不影响围护结构总热惰性指标值.

$ \sum D = {D_1} + {D_2} + \cdots + {D_n}, $

式中:D₁, D₂，…, D_n为各层材料的热惰性指标.

在多层匀质材料层组成的围护结构内，温度波的总衰减为每层材料温度波衰减的乘积.求解其总温度波衰减的复变函数十分复杂，为满足工程计算，由理论精确解处理成工程近似计算，假设围护结构中各层材料的热惰性指标D_n均大于1，将温度波衰减的复变函数化为实数形式，得到温度波在多层材料围护结构内的衰减倍数ν和延迟时间ξ₀计算式^[11]为：

$ \begin{array}{l} \nu = 0.9{{\rm{e}}^{\frac{{\sum D }}{{\sqrt 2 }}}}\frac{{{S_1} + {\alpha _{\rm{i}}}}}{{{S_1} + {Y_1}}} \times \frac{{{S_2} + {Y_1}}}{{{S_2} + {Y_2}}} \cdots \\ \;\;\;\;\;\;\frac{{{S_n} + {Y_{n - 1}}}}{{{S_n} + {Y_n}}} \times \frac{{{Y_n} + {\alpha _{\rm{e}}}}}{{{\alpha _{\rm{e}}}}}, \end{array} $

(15)

$ \begin{array}{l} {\xi _0} = \frac{1}{{15}}\left( {57.3\frac{{\sum D }}{{\sqrt 2 }} - \arctan \frac{{{\alpha _{\rm{i}}}}}{{{\alpha _{\rm{i}}} + \sqrt 2 {Y_{\rm{i}}}}} + } \right.\\ \;\;\;\;\;\;\;\left. {\arctan \frac{{{Y_{\rm{e}}}}}{{{Y_{\rm{e}}} + \sqrt 2 {\alpha _{\rm{e}}}}}} \right). \end{array} $

(16)

式中：α_i为内表面对流换热系数，W/(m²·℃)；Y_e为围护结构外表面蓄热系数，W/(m²·℃)；其他符号意义同上.

对比式(15)、(16)与式(11)、(13)可见，多层材料围护结构与单层匀质材料围护结构不同之处在于，其ν和ξ₀值不仅受D值影响，而且还受材料层排列顺序的影响.

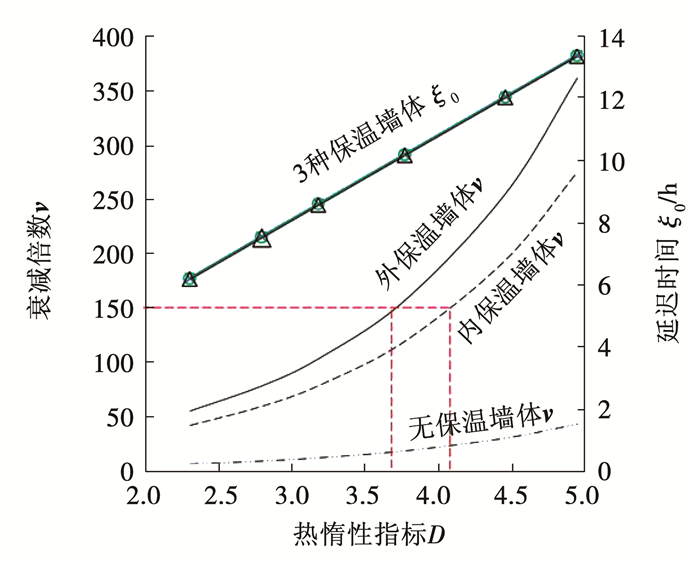
有研究表明，热阻相同墙体，采用不同的材料和排列顺序，其热惰性不同^[15].本文以外保温、内保温及无保温3种不同墙体构造为例，在墙体热阻相同的条件下，计算ν和ξ₀随D的变化.取结构层为钢筋混凝土，其物性参数λ=1.74 W/(m·℃)，ρ=2 500 kg/m³，C=0.92 kJ/(kg·℃)，S₂₄=17.2 W/(m²·℃)；保温层为聚苯乙烯板，其物性参数λ=0.04 W/(m·℃)，ρ=18 kg/m³，C=1.38 kJ/(kg·℃)，S₂₄=0.27 W/(m²·℃)；其中，无保温墙体即为单层匀质材料围护结构，计算结果如图 5所示.

由图 5可见：1)对于同一种形式的围护结构，D值越大，ν越大，ξ₀越长，ξ₀与D值呈正比关系；2)对于不同构造的围护结构，当D值相同时，ξ₀值基本相同，说明多层材料与单层材料围护结构内的温度波数量基本相同，主要受D值影响，单层和多层材料围护结构内的温度波数量n与D的关系式都可用式(14)表达；3)当D值相同时，多层材料围护结构的ν值远超过单层材料围护结构，说明材料类型和排列顺序对ν值具有较大影响；4)存在围护结构D值不同，但ν值相同的情况.例如，内保温墙体D=4.1时，其ν=150，而外保温墙体D=3.7时，也可以获得ν=150.

对于多层材料围护结构，D值越高，只表明延迟时间ξ₀越长，但不能说明衰减倍数ν越大.欲达到良好的热稳定性能，不仅需要高D值，还需要材料层合理的排列顺序，外保温比内保温围护结构能获得更大的衰减倍数，热稳定性能相对良好.

4 结论

1) 热惰性指标与围护结构内温度波衰减和热流密度波衰减的关系式，以及热惰性指标与围护结构内温度波数量的关系式，为热惰性指标量化计算围护结构对温度波动的抵抗能力提供理论依据.

2) 对于相同形式的围护结构，热惰性指标越大，衰减倍数及延迟时间越大，温度波数量越多，围护结构热稳定性越好；对于多层材料围护结构，衰减倍数不仅受热惰性指标影响，还受材料层排列顺序的影响，热惰性指标相同的外保温围护结构比内保温围护结构的衰减倍数较大，热稳定性相对良好.

3) 热惰性指标对于提出温度剧烈波动层具有关键作用，利用热惰性指标D=1来确定温度剧烈波动层厚度，为围护结构有效蓄热设计提供了新思路.

4) 内表面蓄热系数的计算需要通过热惰性指标确定剧烈波动层边界的位置，从而取用合适的计算式；内表面蓄热系数主要与剧烈波动层内材料热工特性有关，整个围护结构的热惰性指标高，内表面蓄热系数值不一定大.