2. 地震工程与工程振动重点实验室(中国地震局),哈尔滨 150080
2. Key Lab of Earthquake Engineering and Engineering Vibration(China Earthquake Administration), Harbin 150080, China
增量动力分析方法[1](IDA)是结构抗倒塌易损性分析的主要手段,而地震动选取是地震动不确定性的主要控制环节以及目标场地地震危险性的主要体现,直接影响到后期的抗倒塌易损性概率计算.目前IDA强震记录选取中常采用3种方法之一:1)粗略限制地震动特性范围,以目标场址地震危险性分析得到的设定地震为依据,确定震级和震中距(M-R)一定范围内的强震记录[2];2)依据美国应用技术委员会(ATC,applied technology council)开展了一项名为“建筑结构抗震性能指标评估”的研究报告(ATC63)中建议的限制条件,依据震级、断层类型以及场地等参数上进行遴选得到数据库[3];3)直接采用ATC63报告推荐的22组远场强震记录作为备选记录库[4].强震记录数量积累到目前阶段,仅仅依靠地震动参数进行限制(方法1和方法2)往往过于宽泛,虽然能体现部分场地特征,但导致备选强震记录数量过多[5],地震动不确定性也无法量化和评估,往往会导致抗倒塌易损性结果不具有鲁棒性.而方法3虽然有利于得到一般适用的结果,但忽略了对目标场址潜在地震动特性的考虑,不利于与最新一代性态工程后续环节衔接[6].综上,在强震记录选取中在控制地震动参数外,通过体现场址危险性特征的目标谱对谱型进行控制就显得尤为重要.
2011年Baker[7]提出了条件均值谱(CMS)概念,基于概率地震危险性分析(PSHA)结果构建目标地震危险性水平下具有真实谱型特征的目标谱.相比传统的一致概率谱(UHS)和规范谱,摒弃了其内在的保守性、包络性及谱型模型化等特点[8].2013年Chandramohan等[9]以CMS谱为目标谱基于条带法和IDA方法研究了二榀五层钢框架结构抗倒塌易损性.而国内对CMS谱的研究及在易损性中的运用还处于起步阶段.陈波[10]通过弹塑性时程分析验证了CMS谱对于结构响应离散性控制的作用.冀昆等[11]从实际地震安全性评价工程现有产出出发,利用中国PSHA的结果进行设定地震解耦,得到了适用于中国现行危险性分析框架思路的条件均值谱.
本文在课题组已有研究基础上,将CMS谱的概念引入到中国结构抗倒塌易损性分析中,对中国传统的IDA计算中的强震记录选取环节进行了改进.以3个不同周期平面框架为算例,在中国两个不同城市工程的地震安全性评价工作基础上构建CMS谱,进行IDA倒塌易损性分析,并将与一致概率谱、规范谱以及ATC63数据集得到的结果进行讨论.
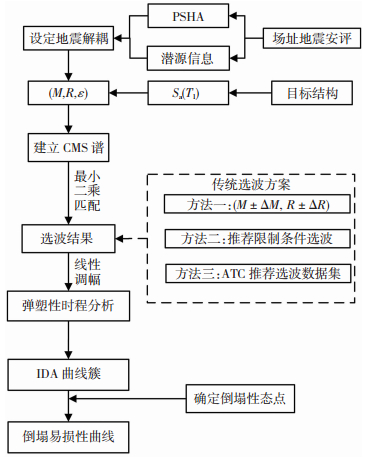
1 基于IDA中强震记录选取的条件均值谱方法本文将中国CMS谱的选波方法与中国传统的IDA方法相结合, 并对其中的选波环节进行修改,从而得到基于IDA中强震记录选取的条件均值谱方法(图 1),改进后方法描述如下:
|
图 1 基于CMS谱选波基础下的IDA计算流程 Figure 1 Calculation flow of IDA method for CMS |
1) 建立结构模型并获取其自振周期T1.
2) 从PSHA及UHS谱中获取T1时的Sa(T1),同时根据附近潜源分布解耦得到对应的M和R.
3) CMS谱构造公式[7]为
| $ \begin{array}{l} {\mu _{{\rm{ln}}{\mathit{S}_{\rm{a}}}\left( {{T_i}} \right)\left| {{\rm{ln}}{\mathit{S}_{\rm{a}}}\left( {{T_1}} \right)} \right.}}{ = }{\mu _{{\rm{ln}}{\mathit{S}_{\rm{a}}}\left( {M,R,{T_i}} \right)}} + \\ \;\;\;\;\;{\rho }\left( {\varepsilon \left( {{T_i}} \right),\varepsilon \left( {{T_1}} \right)} \right)\varepsilon \left( {{T_1}} \right){\sigma _{{\rm{ln}}}}{S_{\rm{a}}}\left( {M,{T_i}} \right), \end{array} $ | (1) |
式中:μlnSa(M, R, Ti)为由衰减关系确定平均加速度谱值,ε(Ti)为目标超越概率下的UHS谱值InSa(Ti)与μlnSa(M, R, Ti)之差与该周期点对数谱值标准差σlnSa(M, Ti)的比值[7](式(2)).各周期点之间ε(Ti)的关系为ρ(ε(Ti), ε(T1)).
| $ \varepsilon \left( {{T_i}} \right) = \frac{{{\rm{ln}}{\mathit{S}_{\rm{a}}}\left( {{T_i}} \right) - {\mu _{{\rm{ln}}}}{\mathit{S}_{\rm{a}}}\left( {M,R,{T_i}} \right)}}{{{\sigma _{{\rm{ln}}{\mathit{S}_{\rm{a}}}}}\left( {M,{T_i}} \right)}} $ | (2) |
4) 以罕遇地震的50 a 2%超越概率为目标危险性水平构建条件均值谱,采用全周期最小二乘法匹配方法从由中国NSMONS强震记录数据库和美国NGA-west1数据库组成的新数据库中选取与之相匹配的一定数量的强震记录[12].
5) 选取结构T1的谱加速度值Sa(T1)作为IM指标,结构最大层间位移角θmax作为损伤指标DM[13].
6) 对每条强震记录以IM指标作为目标进行等步长线性调幅后,进行非线性时程分析,得到若干条与IM指标相关的曲线簇,即为IDA曲线簇.
7) 在IDA曲线上确定倒塌性态点,一般取IDA斜率小于等于初始弹性斜率20%的θmax以及0.10的较小值,来获取各倒塌性态点IM值.
8) 根据最大似然估计法计算IM的对数均值以及对数标准差[14]:
| $ {\rm{ln}}\hat \theta = \frac{1}{n}\sum\limits_{i = 1}^n {{\rm{lnI}}{{\rm{M}}_i}} , $ | (3) |
| $ \hat \beta = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left( {{\rm{ln}}\left( {{\rm{I}}{{\rm{M}}_i}/\hat \theta } \right)} \right)} } . $ | (4) |
9) 结构抗倒塌易损性计算:将
| $ P\left( {C\left| {C\left| {{\rm{IM = }}\mathit{x}} \right.} \right.} \right) = \Phi \left( {\frac{{{\rm{ln}}\left( {x/\hat \theta } \right)}}{{\hat \beta }}} \right). $ | (5) |
根据GB 50011—2010《建筑抗震设计规范》[15]及JGJ 3—2010《高层建筑混凝土结构技术规程》[16]等规范要求,本文采用PKPM软件分别设计了三层、八层及十五层等3种钢混框架结构,平面图、中间一榀框架、梁柱截面尺寸以及配筋见图 2. 3种结构的首层层高4.5 m,其余层高均为3.3 m,楼板厚度为120 mm.结构梁、柱和楼板均为现浇,混凝土等级为C40,纵筋采用HRB335,箍筋采用HPB235.结构顶层恒载4.0 kN/m2,活载2.0 kN/m2;其余层恒载6.0 kN/m2,活载2.0 kN/m2.建筑场地均为Ⅰ类,抗震设防烈度7度,设计基本地震加速度0.10 g,设计地震分组第二组.本文基于OpenSees软件对3种结构进行数值模拟分析,其中3种框架结构的自振周期及有效质量参与系数见表 1.由于结构平面对称,故只选用其中一榀框架进行数值分析.混凝土本构关系采用concrete02,钢筋本构关系采用steel02.

|
图 2 结构模型 Figure 2 Model of Structure |
| 表 1 算例结构自振周期及有效质量参与系数 Table 1 Structural natural periods and effective mass participation coefficient |
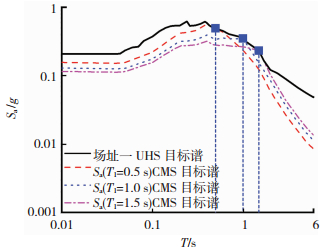
选取位于河北省廊坊地区(场地一)以及四川省雅安地区(场地二)作为算例对上述方法进行示例说明,两个地区的地理位置分别为N39.309°/E116.502°和N29.795° /E102.846°,设防烈度均为7度,设计基本地震加速度0.10 g,设计地震分组第二组.以目标场址250 km范围内的潜源为研究对象,场地一潜源的地震带均为华北平原地震带,地震活动参数a值为4.2,b值为0.83;场地二潜源存在两个地震带,一个为龙门山地震带(a值为5.2,b值为0.716),另一个为鲜水河东淀地震带(a值为33.1,b值为0.855).地震动衰减关系采用在中国地震安全性评价工程中广泛使用的霍俊荣(1989)[17]的西南地区和华北地区衰减关系.安全性评价中通过PSHA得到这两个地区50 a 2%超越概率的UHS谱.根据PSHA解耦,分别得到3种结构在场地一和场地二下该危险性水平下的平均设定地震解耦结果,见表 2.根据式(1)构建对应的50 a 2%超越概率下不同目标周期点条件均值谱.图 3为场地一的UHS谱以及各个周期点的CMS谱.
| 表 2 50 a 2%超越概率下设定地震解耦结果 Table 2 Deaggregation results for 50 a 2% exceedance probability |
|
图 3 场地一的UHS目标谱与对应CMS谱 Figure 3 UHS and CMS for the first site |
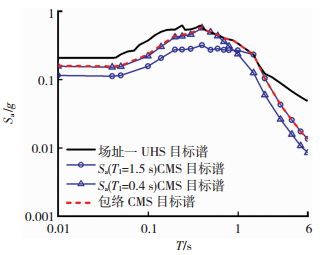
对于长周期结构来说,准确估计结构响应必须考虑高阶振型影响,而CMS谱无法同时兼顾多个振型周期点反应谱地震危险性相同的[8],为了避免该问题对本文长周期算例结构的影响,参考国外学者的做法[18],采用多周期CMS谱包络的方法来解决该问题.在确定参与高阶振型周期T1,T2…Tn后,分别对Sa(T1),Sa(T2),Sa(Tn)进行地震危险性概率分析(PSHA)解耦以及CMS谱构建;最后对各个周期点条件谱之间的部分用UHS谱进行包络处理.这种基于多条CMS谱包络组合的方法在最小程度“损害”CMS谱的谱型真实性的前提下,采用UHS谱进行包络处理,在较好考虑高阶振型影响的同时保证了主要考虑振型点的超越概率一致,对于考虑二到三阶振型的结构具有较好的适用性,当考虑振型过多时,其有效性仍待进一步研究.根据中国现行抗震规范,以90%振型参与系数作为标准来判断参与振型,对于0.5 s和1.0 s结构来说,仅考虑一阶振型即已超过或近似达到了90%,而对于1.5s结构来说,需要同时考虑T1=1.5 s和T2=0.4 s两阶振型,以Sa(T1=0.4 s)重新构建CMS谱,得到最终两个场地的包络CMS谱.图 4为场地一的包络CMS谱.
|
图 4 场地一包络CMS谱构造示意 Figure 4 Schematic diagram for envelop CMS |
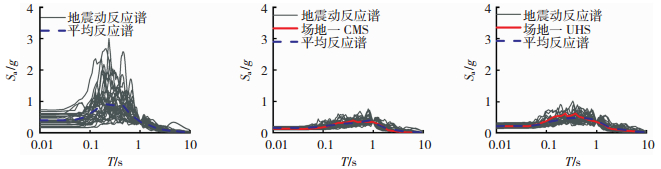
在进行目标谱匹配之前,首先参照本文的设定地震解耦结果对强震记录的M和R的范围进行约束来缩小备选记录范围.在对目标周期进行线性调幅后,采用最小二乘法对CMS目标谱、UHS目标谱以及规范设计谱进行匹配,逐条进行目标谱与记录反应谱的误差平方和计算,然后选取误差最小的30条强震记录作为最终结果,以场地一的八层结构为例,给出了UHS谱和CMS谱的匹配结果见图 5,同时作为对比,给出了ATC63数据集的强震记录反应谱结果以及对应的平均谱.可以看到,不同Sa(T1)周期下归一化后的ATC63选波数据集结果离散性明显大于通过目标谱控制选取强震记录的离散性,而CMS谱由于其内在谱型的合理性,得到的匹配结果不仅离散性最小,而且平均反应谱在全周期段均更加贴近目标谱[15],而UHS谱由于其内在谱型的不真实或者说偏向保守,在非目标周期段与平均目标谱还是出现了一些偏差,而且记录之间的离散性也更大.
|
图 5 场地一八层结构不同目标谱选波结果与ATC63推荐记录数据集 Figure 5 Ground-motion selection records matching different target spectrum and ATC63 for 8-layer structure at the first site |
对三层、八层以及十五层结构在不同强震记录集下进行IDA计算分析.并根据式(3)和(4)计算各个工况对应的平均倒塌性态点对应Sa(T1)估计值
| 表 3 八层结构场地一的倒塌性态点参数 Table 3 Parameters of 8-layer structure at the first site |
通过式(5)获得3种结构在不同强震记录集下的抗倒塌易损性曲线,见图 6.规范谱得到的抗倒塌易损性概率曲线最陡峭,UHS谱与ATC63数据集得到的次之,CMS谱对应的最平缓.计算不同选波工况下倒塌超越概率P = 0.16、0.50和0.84处对应的Sa(T1)值以及本文CMS谱选波结果下与ATC数据集的相对误差(%),对于短(0.5 s)和中周期(1.0 s)结构来说,在两种场地下CMS谱在P = 0.16处Sa(T1)的低估比例为10%~20%,P = 0.50处低估比例为10%~15%,P = 0.84处低估比例在10%以内.而长周期(1.5 s)结构,两个城市基于单条CMS谱的计算结果在P=0.16、0.50和0.84处的低估比例均超过20%,这一比例在雅安地区算例一度达到了45%,这显然过于低估了实际的倒塌危险性,而本文采用包络CMS谱来考虑两阶振型的影响,最终计算结果超越概率低估比例约为18%、14%和8%,与中短周期结构的低估程度相仿.这一对比案例说明,对于长周期结构来说,如果不考虑高阶振型的影响,与ATC63计算结果相比,单条CMS谱的倒塌易损性计算结果可能显著低估同倒塌的超越概率,容易造成偏危险的性态分析结果.

|
图 6 抗倒塌易损性曲线 Figure 6 Collapse fragility probability curves |
1) 以中国现行地震安全性评价工作为基础进行设定地震解耦工作,进而建立50 a 2%超越概率对应的CMS谱,最后进行最小二乘法匹配得到各个幅值下的强震记录数据集并应用到后续IDA计算中.所得到的强震记录数据集考虑了不同目标场址的地震危险性差异.
2) 以自振周期分别为0.5、1.0和1.5 s的二维平面框架为目标结构,基于中国两个城市的地震安全性评价工作构建CMS谱,选波结果与当地50 a 2%超越概率的一致概率谱以及罕遇地震规范谱进行对比后发现,由于CMS谱内在谱型的合理性,得到的匹配结果离散性最小且平均反应谱在整个全周期段均更加贴近目标谱.ATC63数据集记录之间的离散性远大于通过目标谱控制的选波结果数据集.
3) 对两个算例进行抗倒塌易损性分析后发现,基于规范谱得到的抗倒塌易损性概率曲线最陡峭,而基于UHS谱与ATC数据集次之,CMS最平缓.对于短(0.5 s),中周期(1.0 s)结构来说,基于CMS谱的选波结果在P=0.16处倒塌点对应的Sa(T1)比ATC63数据集低10%~20%,P=0.50处低10%~15%,P=0.84处低10%以内.
4) 对于较长周期的1.5 s结构,本文采用包络CMS谱来考虑高阶振型的影响,通过与单周期点CMS谱结果进行对比后发现,后者的抗倒塌易损性计算结果显著低估实际的倒塌超越概率,容易造成偏危险的性态分析结果.
综上,本文采用的基于中国CMS谱的强震记录选取方法是对中国现有IDA选波方法的补充,使地震危险性与中国结构易损性良好衔接,所得易损性分析结果因所选强震记录考虑了场址地震危险性更能体现目标结构的实际地震风险水平.
| [1] |
于晓辉, 吕大刚. 考虑结构不确定性的地震倒塌易损性分析[J]. 建筑结构学报, 2012, 33(10): 9. YU Xiaohui, LÜ Dagang. Seismic collapse fragility analysis considering structural uncertainties[J]. Journal of Building Structures, 2012, 33(10): 9. |
| [2] |
吴巧云, 朱宏平, 樊剑. 基于性能的钢筋混凝土框架结构地震易损性分析[J]. 工程力学, 2012, 29(9): 120. WU Qiaoyun, ZHU Hongping, FAN Jian. Performance-based seismic fragility analysis of RC frame structures[J]. Engineering Mechanics, 2012, 29(9): 120. |
| [3] |
于晓辉, 吕大刚, 王光远.关于概率地震需求模型的讨论[J].工程力学, 2013, 30(8): 174 YU Xiaohui, LV Dagang, WANG Guangyuan. Discussions on probabilistic seismic demand models, 2013, 30(8): 174 |
| [4] |
施炜, 叶列平, 陆新征, 等. 不同抗震设防RC框架结构抗倒塌能力的研究[J]. 工程力学, 2011, 28(3): 42. SHI Wei, YE Lieping, LU Xinzheng, et al. Study on the collapse-resistant capacity of RC frames with different seismic fortification levels[J]. Engineering Mechanics, 2011, 28(3): 42. |
| [5] |
马海滨, 卓卫东, 林杰, 等. 基于云图法的规则桥梁概率地震需求模型[J]. 工程力学, 2016, 33(增刊1): 121. MA Haibin, ZHUO Weidong, LIN Jie, et al. A probalilistic seismic demand model for regular highway bridges by cloud approach[J]. Engineering Mechanics, 2016, 33(S1): 121. |
| [6] |
王敏, 朱爱萍, 丁袁媛, 等. 考虑地面运动不确定性的地面运动记录选择方法研究[J]. 土木工程学报, 2016(9): 43. WANG Min, ZHU Aiping, DING Yuanyuan, et al. Study on method for ground motion selection considering uncertainties of ground motions[J]. China Civil Engineering Journal, 2016(9): 43. DOI:10.15951/j.tmgcxb.2016.09.005 |
| [7] |
BAKER J W. Conditional mean spectrum: tool for ground-motion selection[J]. Journal of Structural Engineering, 2011, 137(3): 323. DOI:10.1061/(ASCE)ST.1943-541X.0000215 |
| [8] |
KWONG N S, CHOPRA A K. A generalized conditional mean spectrum and its application for intensity-based assessments of seismic demands[J]. Earthquake Spectra, 2016, 33(1): 124. DOI:10.1193/040416EQS050M |
| [9] |
CHANDRAMOHAN R, BAKER J W, DEIERLEIN G G. Quantifying the influence of ground motion duration on structural collapse capacity using spectrally equivalent records[J]. Earthquake Spectra, 2016, 32(2): 936. |
| [10] |
陈波.结构非线性动力分析中地震动记录的选择和调整方法研究[D].北京: 中国地震局地球物理研究所, 2013: 112 CHEN Bo. Ground motion selection and modification methods for performing nonlinear dynamic analysis of buildings[D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2013: 112 |
| [11] |
冀昆, 温瑞智, 任叶飞. 中国地震安全性评价中天然强震记录选取[J]. 哈尔滨工业大学学报, 2016, 48(12): 184. JI Kun, WEN Ruizhi, REN Yefei. Real strong ground-motion selection for Chinese seismic safety evaluation work[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 184. DOI:10.11918/j.issn.0367-6234.2016.12.000 |
| [12] |
EADS L, MIRANDA E, KRAWINKLER H, et al. An efficient method for estimating the collapse risk of structures in seismic regions[J]. Earthquake Engineering & Structural Dynamics, 2013, 42(1): 25. |
| [13] |
VAMVATSIKOS D, CORNELL CA. Incremental dynamic analysis[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 494. |
| [14] |
BAKER J W. Efficient analytical fragility function fitting using dynamic structural analysis[J]. Earthquake Spectra, 2015, 31(1): 582. DOI:10.1193/021113EQS025M |
| [15] |
建筑抗震设计规范: GB 50011—2010[S].北京: 建筑工业出版社, 2006: 162 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010: 162 |
| [16] |
高层建筑混凝土结构技术规程: JGJ 3—2010[S].北京: 中国建筑工业出版社, 2011: 55 Technical specification for concrete structures of tall building: JGJ 3—2002[S]. Beijing: China Architecture & Building Press, 2011: 55 |
| [17] |
霍俊荣.近场强地面运动衰减规律的研究[D].哈尔滨: 中国地震局工程力学研究所, 1989: 206 HUO Junrong. Study on the near-field strong ground motion attenuation relationship[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 1989: 206 |
| [18] |
CARLTON B, ABRAHAMSON N. Issues and approaches for implementing conditional mean spectra in practice[J]. Bulletin of the Seismological Society of America, 2014, 104(1): 504. DOI:10.1785/0120130129 |
 2018, Vol. 50
2018, Vol. 50


