2. 天津市成像与感知微电子技术重点实验室(天津大学),天津 300072
2. Tianjin Key Laboratory of Imaging and Sensing Microelectronic Technology (Tianjin University), Tianjin 300072, China
机载激光雷达(Laser Detection And Ranging, LADAR),是一种主动式探测技术,集激光扫描测距技术、全球定位系统技术、惯性导航技术等于一体,通过记录发射和接收激光脉冲之间的时间差来计算目标距离,从而计算出物体的三维坐标[1-2],具有测量效率高、灵活性高等特点,基本不受地形条件的限制,因而成为各种测量应用中深受欢迎的高新技术.
当地物或地形较复杂时,回波幅度变动较大,通过预先设定阈值来实现时间测量的TDC(Time-to-Digital Converter)技术[3]已不再适用,且对于机载推扫式激光雷达系统来说,不宜采取多次测量求均值的方法来提高测量精度,否则会引进测量时间长以及数据量大等问题[4],因此,如何精确、稳定、实时地提取出回波时刻是机载激光雷达系统信号处理的关键问题.
目前应用的回波时刻提取算法可以分为两大类,一类主要包括前沿判别法、恒比定时法等[5],这类算法都将回波定位在采样点的某个时刻,精度完全受系统采样率的限制,且易受噪声、信号强度波动以及回波展宽的影响,但运算比较简单,适用于对精度要求不高的测距系统;另一类是全波形分析的算法,包括波形形心算法、高斯拟合算法等,是利用多点信息,充分考虑回波的形状,运用更复杂的算法进行计算,突破采样率的限制,理论上精度更高且抗噪性能更强.从数学理论上分析,高斯拟合算法需要预先根据波形数据合理设定高斯函数中各参数的初始值,然后利用最小二乘法更新迭代高斯函数中的所有参数,求出最优解,拟合结果依赖初值的设定且迭代过程繁琐[6-7],虽然精度较高但迭代运算耗时较长,且在硬件实现时难度较高,目前的相关研究均停留在上位机阶段.而形心算法是利用时间加权平均法来进行回波时刻的提取,由于算法简单、执行速度快,被广泛采用和研究[5, 8-9].与高斯拟合算法相比,形心算法仅包括乘除等基本运算,因此在硬件实现时时间复杂度和空间复杂度都表现出优势,然而形心算法在硬件实现时精度会明显降低,难以满足高精度的测距要求.目前针对形心算法的改进主要有“双尺形心法”,即利用形心法计算波峰附近的处于一定宽度窗口内的那部分波形的形心时刻,可有效减弱杂波对形心计算的影响,而对于形心算法的硬件实现及可能存在的问题尚未有详细研究.
本文利用建模所得数据,仿真分析传统形心算法精度,由于硬件实现时存在数据精度受损问题,导致算法易受噪声影响,因此提出一种基于中位数法的波形形心修正算法,并将此算法在FPGA中实现,基于板级进行验证.
1 机载激光雷达测量技术 1.1 回波信号建模对于脉冲激光雷达,可以采用高斯函数及特征参数近似描述有效脉冲回波模型[10-11].
| $ P\left( t \right) = {P_{\rm{s}}}\frac{{{P_{\rm{e}}}}}{{{T_0}}}\sqrt {\frac{{\rm{k}}}{\pi }} {\rm{exp}}\left( { - k\frac{{{{\left( {t - {T_{\rm{r}}}} \right)}^2}}}{{2T_0^2}} } \right)+ N{\rm{n}}. $ | (1) |
式中:Ps为回波能量衰减系数,Pe为激光发射能量,T0为激光脉冲宽度,常数k为4ln2,tr为回波时刻,Nn为噪声. Ps可用式(2)计算
| ${P_{\rm{s}}} = \frac{{T_{{\rm{atm}}}^2{A_{\rm{R}}}{\eta _{\rm{e}}}{\eta _{\rm{r}}}{L_{\rm{s}}}{\rm{co}}{{\rm{s}}^2}\left( \theta \right)}}{{\pi {h^2}}}. $ | (2) |
式中:Tatm2为大气双程损失,AR为探测器接收面积,ηe为发射光学效率,ηr为接收光学效率,θ为扫描角,Ls为目标反射率,h为飞机飞行高度.
在实际测量时,信号中会存在背景噪声、探测器噪声、量化噪声等非理想因素,这里统一表示为Nn.采用高斯白噪声,对背景噪声及探测器噪声进行建模[11],考虑到不同信号质量,设定不同信噪比(signal-to-noise ratio,SNR),之后基于8 bits量化位数对混有噪声的回波信号进行量化,实现量化噪声建模,得到量化码值.此处加入量化噪声的建模,使得建模数据更接近实测值,利于算法的具体分析.
1.2 传统形心算法形心被认为是可以平衡波形形状的存在于回波中的一个虚拟的点,形心的位置与数据长度l以及回波脉冲的形状及位置有关[13],应用波形数据f(t, y)计算形心表达式为
| $ C = \frac{{\int {f\left( {t, y} \right)} {\rm{d}}\mathit{l}}}{{\int {{\rm{d}}\mathit{l}} }}. $ | (3) |
式中C的计算结果隐含回波形状的信息,受计算数据长度以及回波采样点的相对强度的影响.因此为降低信号中噪声对形心计算的影响,提高回波脉冲形心的计算精度,预先利用发射脉冲参数对回波进行初步定位,即利用一定数据长度的窗宽,滑窗找到强度最大的区域,然后依据窗宽内数据进行计算,先后利用形心算法即可得到发射时刻和回波时刻,从而实现测距.
窗宽会影响形心计算的精度,而窗宽的选取受回波信号脉冲宽度及系统采样率的影响.基于5 ns脉冲宽度,2G SPS的系统背景,设定窗宽为15.在实际应用中,脉冲回波数据来自ADC的量化输出,此时数据精度受到限制,且在测试环境中,噪声的存在会使得形心计算结果出现漂移现象,将很大程度上影响系统精度,因此为提高在硬件实现中传统形心算法的精度,提出基于中位数法修正的形心算法.
1.3 基于中位数法修正的形心算法中位数用于有序数据,可有效阻止极端情形所施加的过分影响,适用于揭示最接近真实情形的系统状态,具有较好的稳健性,可有效提高算法对噪声影响的不敏感性[14-15].基于如下步骤对传统形心算法进行修正:
步骤1 以窗宽l对脉冲信号进行初步定位,得到波形数据y = [y1, y2, …, yl],以及对应时间数据t = [t1, t2, …, tl];
步骤2 根据式(3)计算步骤1中窗口内波形数据形心的时刻值t0,同时计算出窗口内时间数据的中位数tm =median([t1 t2…tl]);
步骤3 计算步骤2中的形心t0与中位数tm的差量d=tm-t0,根据差量d与临界值ε的大小关系对形心计算结果进行判断与修正,t0*为形心的最终计算结果,修正量为Δt,依据式(4)进行判断修正
| $ t_0^ * = \left\{ \begin{array}{l} {t_0} - \mathit{\Delta }t, \;\;\;\;\;\;\;\;d \le - \varepsilon ;\\ {t_0} + \mathit{\Delta }t, \;\;\;\;\;\;d \ge \varepsilon ;\\ {t_0}, \;\;\;\;\;\; - \varepsilon < d < \varepsilon . \end{array} \right. $ | (4) |
步骤4 利用步骤1~3对发射脉冲以及回波信号依次进行形心的修正,进而得到修正后的激光飞行时间.
综上所述,应用中位数法实现对形心的修正,可以避免由于数据精度降低以及随机噪声对形心计算的影响[14],有效提高算法的精度以及稳定性.
2 算法仿真分析在实验中,以高斯拟合算法为基准,分析对比传统形心算法、修正形心算法的精度.仿真结果中高斯拟合算法的拟合优度为99%以上,因此基准数据可靠.
对于同一波形,同时记录三种算法的仿真结果,再将其与真值的差值作为误差.考虑到热噪声的随机性,为分析算法的稳定性,在波形数据准备时,本文针对信噪比为5~20 dB的情况,以1 dB为步长,在MATLAB中,分别进行10 000次仿真建模生成原始数据,用于分析算法的精度.
利用生成的10 000组原始数据进行仿真实验,并统计不同信噪比下激光飞行时间的最大误差,见图 1所示.信噪比提高,三种算法的精度均会提高,信噪比较低时,高斯拟合算法更精确.信噪比为5 dB时,传统形心算法具有0.9 ns左右的理论精度,修正形心算法为0.5 ns,精度提升45%,高斯拟合算法具有0.3 ns理论精度;信噪比较高时,传统形心算法无需修正,且较高斯拟合算法更精确,信噪比为20 dB时,两种形心算法均具有0.01 ns理论精度,高斯拟合算法具有0.06 ns理论精度.本文进一步统计信噪比为5 dB时三种算误差均值以及标准差[12, 16],见表 1.

|
图 1 传统形心算法、修正形心算法与高斯拟合算法的最大测时误差统计对比 Figure 1 Comparison of maximum error of traditional centroid algorithm, corrected centroid algorithm and Gaussian fitting algorithm |
| 表 1 算法精度统计 Table 1 Algorithmic precision statistics |
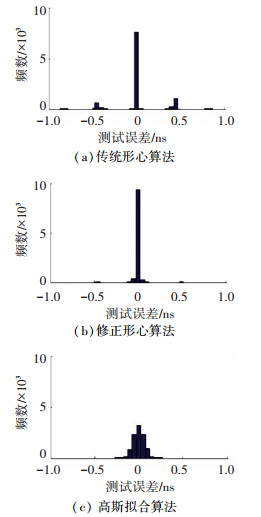
从表中结果可看出,修正形心算法的误差均值以及标准差明显小于传统形心算法,并且小于高斯拟合算法误差的标准差.本文同时统计出信噪比为5 dB时三种算法的误差分布,见图 2.
|
图 2 误差统计直方图 Figure 2 The error statistics histogram of algorithms |
结合图 1、2分析,可得结论为:高斯拟合算法的误差服从正态分布,而形心算法不论是否进行修正,在信噪比较低时的误差都会分布在不连续区段内,出现小概率误差较大的情况.信噪比为5 dB时,传统形心算法误差多数分布在较精确的0.1 ns以内,少数分布在±0.4 ns以及±0.8 ns左右,修正形心算法误差仅有少数分布在±0.4 ns左右,这是前文所说的修正形心算法的标准差低于高斯拟合算法的本质原因.
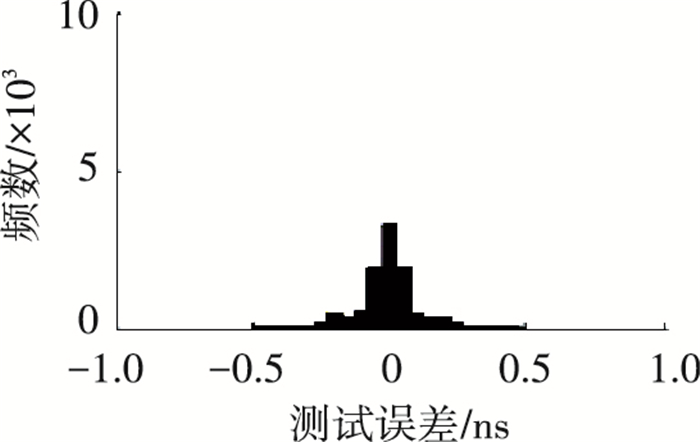
进一步分析传统形心算法的误差分布,确定这种分层现象是量化处理导致的. 图 3是在信噪比为5 dB时,未进行量化处理的波形数据对应的传统形心计算误差统计图.
|
图 3 无量化处理对应的传统形心算法误差统计 Figure 3 Error statistical histogram oftraditional centroid algorithm for non-qualified processing |
如图 3所示,波形数据未量化处理的传统形心算法计算结果,在统计时并未出现分层现象,且实现的算法精度更高,信噪比为5 dB时,最大误差为0.5 ns.这是由于量化位数越高,量化码值相对于原始数据的精度损失就越少,对应的计算误差也越小,但对于ADC器件来说,高采样率与高分辨率无法兼顾.因此,传统形心算法的分层现象在基于高速ADC的数据处理系统中无法避免,本文提出的基于中位数法修正的形心算法可有效减弱分层现象,提高算法的精度,在硬件设计上具有一定实用性.
3 算法硬件验证搭建测试平台:使用信号发生器DG5072作为信号源来模拟激光器,输出5 ns脉宽的电信号来模拟激光信号,利用图 4所示测试板,进行数据采样与处理,验证修正形心算法的精度.

|
图 4 测试板 Figure 4 Test board |
利用测试平台对模拟的激光脉冲信号进行测试与处理,见图 4.模拟信号经过模数转换器ADC08D1020采样,采样率为2G SPS,输出码值以500 MHz的速度由FPGA控制接收,并运行修正形心算法进行数据处理.
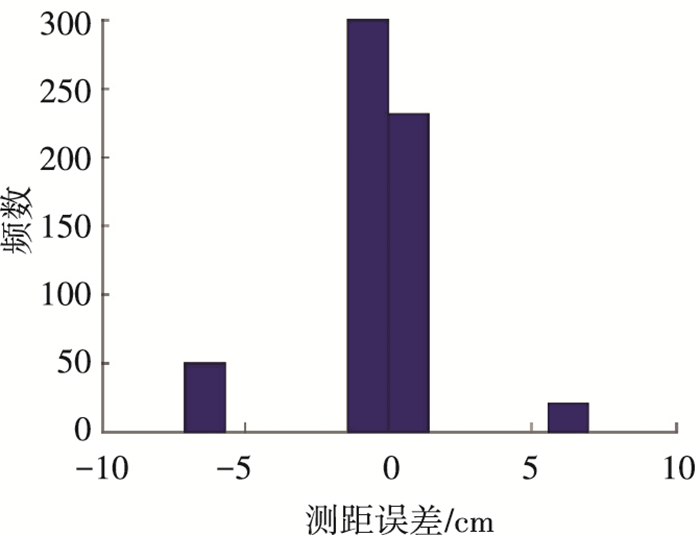
记录多组修正形心算法的计算结果,得到的测量误差见图 5.
|
图 5 修正形心测距误差 Figure 5 Ranging error of corrected centroid |
观察图 5中600次实测结果,形心计算误差分层现象与仿真结果一致,验证了仿真建模的合理性,且实测时误差最大为0.5 ns,对应7.5 cm,验证了修正形心算法的硬件设计的正确性.
4 结论本文提出的基于中位数法的形心修正方法,简洁高效,在计算形心的同时计算中位数,根据形心与中位数的大小关系,做出形心的判断与修正,可有效减弱硬件实现时的形心分层现象,提高算法精度.仿真结果表明,基于中位数法修正后的形心算法精度更高,抗噪性能更好,信噪比为5 dB时,仿真精度可达到0.5 ns,相比较传统形心算法精度提高了45%,信噪比较高时精度高于高斯拟合算法,可实现0.01 ns理论精度.由于基于中位数法修正的形心算法运算简单,易于实现基于FPGA的算法移植,在不增加系统复杂度的前提下有效地提高了激光测距的精度.经过板级验证,修正形心算法可实现±7.5 cm的测距精度,同时证明了算法的实时性优势,满足推扫式机载激光雷达系统实时探测的需求.未来的研究将基于真实激光信号进一步验证提出算法的适用性及稳健性.
| [1] |
MALLET C, BRETAR F. Full-waveform topographic lidar: state-of-the-art[J].
ISPRS Journal of Photogrammetry and Remote Sensing, 2009, 64(1): 1-16.
DOI: 10.1016/j.isprsjprs.2008.09.007 |
| [2] |
王智, 金光, 张立平. 远距离目标位置解算方法的实现[J].
哈尔滨工业大学学报, 2009, 41(07): 215-218.
WANG Zhi, JIN Guang, ZHANG Liping. Realization of location computation of long-distance object[J]. Journal of Harbin Institute of Technology, 2009, 41(07): 215-218. DOI: 10.3321/j.issn:0367-6234.2009.07.051 |
| [3] |
NISSINEN J, NISSINEN I, KOSTAMOVAARA J. Integrated receiver including both receiver channel and TDC for a pulsed time-of-flight laser rangefinder with cm-level accuracy[J].
IEEE Journal of Solid-State Circuits, 2009, 44(5): 1486-1497.
DOI: 10.1109/JSSC.2009.2017006 |
| [4] |
姜海娇, 来建成, 王春勇, 等. 激光雷达的测距特性及其测距精度研究[J].
中国激光, 2011, 38(05): 234-240.
JIANG Haijiao, LAI Jiancheng, WANG Chunyong, et al. Research on ranging property of laser radar and its range accuracy[J]. Chinese Journal of Lasers, 2011, 38(05): 234-240. DOI: 10.3788/CJL201138.0514001 |
| [5] |
李京, 杨小良, 梁谦, 等. 一种基于回波形心位置的激光引信定距方法[J].
航空兵器, 2014(03): 16-19.
LI Jing, YANG Xiaoliang, LIANG Qian, et al. A range finder method for pulse laser fuze based on the center of echo waveform[J]. Aero Weaponry, 2014(03): 16-19. DOI: 10.19297/j.cnki.41-1228/tj.2014.03.005 |
| [6] |
WONG H, ANTONIOU A. Characterization and decomposition of waveforms for larsen 500 airborne system[J].
IEEE Transactions on Geoscience and Remote Rensing, 1991, 29(6): 912-921.
DOI: 10.1109/36.101370 |
| [7] |
赵欣, 张毅, 张黎明, 等. 激光测高仪高斯回波分解算法[J].
红外与激光工程, 2012, 41(03): 643-648.
ZHAO Xin, ZHANG Yi, ZHANG Liming, et al. Algorithm of laser altimeter reflecting waveform based on gaussian decomposition[J]. Infrared and Laser Engineering, 2012, 41(03): 643-648. DOI: 10.3969/j.issn.1007-2276.2012.03.019 |
| [8] |
柯熙政, 雷思琛, 杨沛松. 大气激光通信光束同轴对准检测方法[J].
中国激光, 2016, 43(06): 181-190.
KE Xizheng, LEI Sichen, YANG Peisong. Beam coaxial alignment detection in atmospheric laser communication[J]. Chinese Journal of Lasers, 2016, 43(06): 181-190. DOI: 10.3788/CJL201643.0606003 |
| [9] |
李一芒, 盛磊, 陈云善. 高速激光光斑检测系统的设计与实现[J].
激光技术, 2015, 39(04): 533-536.
LI Yimang, SHENG Lei, CHEN Yunshan. Design and implement of high-speed laser spot detection systems[J]. Laser Technology, 2015, 39(04): 533-536. DOI: 10.7510/jgjs.issn.1001-3806.2015.04.023 |
| [10] |
黄科, 李松, 马跃, 等. 单光子模式激光测高探测概率模型与精度分析[J].
中国激光, 2016, 43(11): 235-240.
HUANG Ke, LI Song, MA Yue, et al. Research on detection probability model of single-photon laser altimetry and its range accuracy[J]. Chinese Journal of Lasers, 2016, 43(11): 235-240. DOI: 10.3788/cj1201643.1110001 |
| [11] |
ABDALLAH H, BAGHDADI N, BAILLY J S, et al. Wa-LiD: a new LiDAR simulator for waters[J].
IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 744-748.
DOI: 10.1109/LGRS.2011.2180506 |
| [12] |
ABDALLAH H, BAILLY J S, BAGHDADI N., et al. Potential of space-borne LiDAR sensors for global bathymetry in coastal and inland waters[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(1): 202-216.
DOI: 10.1109/JSTARS.2012.2209864 |
| [13] |
MUSS J D, AGUILAR-AMUCHASTEGUI N, MLADENOFF D J, et al. Analysis of waveform lidar data using shape-based metrics[J].
IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 106-110.
DOI: 10.1109/LGRS.2012.2194472 |
| [14] |
陶叶青, 高井祥, 姚一飞. 基于中位数法的抗差总体最小二乘估计[J].
测绘学报, 2016, 45(03): 297-301.
TAO Yeqing, GAO Jingxiang, YAO Yifei. Solution for robust total least squares estimation based on median method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(03): 297-301. DOI: 10.11947/j.AGCS,2016.20150234 |
| [15] |
吴骏. 基于数学史的统计概念教学研究-以平均数、中位数和众数为例[D]. 上海: 华东师范大学, 2013.
WU Jun. The study on teaching and learning of statistics concepts based on the history of mathematics-a case of mean, median and mode[D]. East China Normal University, 2013. |
| [16] |
孙蕊, 兰盛昌, 徐国栋. 微小卫星编队的星间测距系统设计及精度分析[J].
哈尔滨工业大学学报, 2009, 41(07): 21-25.
SUN Rui, LAN Shengchang, XU Guodong. Design of inter-satellite ranging system in formation and its precision analysis[J]. Journal of Harbin Institute of Technology, 2009, 41(07): 21-25. DOI: 10.3321/j.issn:0367-6234.2009.07.005 |
 2018, Vol. 50
2018, Vol. 50


