蚁狮优化算法(ant lion optimizer algorithm, ALO)作为一种新的智能算法,于2015年由澳大利亚教授Seyedali提出.它的优势在于调节参数少,全局寻优能力好、收敛速度快和易于实现等方面.与粒子群算法、蝙蝠算法和花朵授粉算法等7种智能算法相比,ALO算法具有更好的全局寻优能力和收敛速度[1].但在寻优进化过程中,算法也存在一些不足,比如:算法初期的轮盘赌搜索方法影响种群的寻优性能和收敛速度; 在迭代过程中,蚂蚁可能向适应度较差的个体进行学习,使算法陷入局部最优,影响算法效率; 算法后期,蚁狮多样性随搜索步长和搜索速度的下降而降低,从而导致算法后期易陷入局部最优解.针对上述问题,众多学者进行了研究.罗钧等[2]结合Logistic混沌方法,改善蜂群的种群多样性和全局寻优能力; Gao等[3]使用Logistic混沌和反向训练方法提高收敛速度和精度; 匡芳君等[4-5]使用Tent混沌方法优化蜂群与粒子群混合算法,克服后期不易获得最优解的缺点; Akay等[6]提出利用参数优化改进人工蜂群算法.
针对ALO算法缺陷,本文借鉴Tent混沌方法[4]、锦标赛选择策略[7]和Logistic混沌映射[3],提出了自适应Tent混沌搜索的蚁狮优化算法(self-adaptive Tent chaos search ant lion optimizer algorithm, SATC-ALO).算法初期,使用Tent混沌策略优化算法,扩大种群搜索区域,保证其均匀性和多样性,同时采取自适应动态调整Tent混沌搜索空间,产生适应度较好的新解,克服算法无法获得全局最优解的缺陷; 使用锦标赛选择策略替代轮盘赌法选择蚁狮,提高种群的优良性能和跳出局部最优的能力; 算法后期,将混沌算子与蚂蚁随机游走的行为结合,生成具有混沌算子遍历性、随机性和规律性特点的混沌蚂蚁[8],结合蚁狮的寻优能力,降低其收敛时间.实验仿真结果表明,该算法优化种群的多样性和均匀性,并能改善ALO算法的收敛时间、收敛精度、搜索效率以及跳出局部最优的能力,在6个基准测试函数和航迹规划问题上均表现出较好的性能,具有实际应用价值.
1 蚁狮优化算法蚁狮优化算法是受到AntLion捕捉蚂蚁的过程的启发:蚂蚁在地上无规律爬行,而AntLion事先在地下做好陷阱等待蚂蚁,当蚂蚁被AntLion捉到后,AntLion会继续挖陷阱等待下一只蚂蚁.
ALO算法即是通过仿照蚁狮捕捉蚂蚁的过程来解决实际问题:蚂蚁通过随意行为对解进行搜索; 通过学习优秀蚁狮以确保取得全局最优值.蚂蚁和蚁狮的位置表示优化问题的解,蚁狮通过不断捕食蚂蚁寻找问题的最优解.蚁狮捕食蚂蚁的行为见图 1所示.

|
图 1 蚁狮的捕食行为 Figure 1 Hunting behaviour of antlions |
寻求最优解时,需要应用以下条件:
1) 蚂蚁随意走动受蚁狮陷阱的牵制;
2) 蚁狮的适应度值越大,陷阱的范围越大,越容易抓到蚂蚁;
3) 如果蚂蚁的适应度值优于蚁狮,表示被蚁狮抓到.
蚂蚁的随机行为表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{X}}\left( t \right) = \left[ {0,{\rm{cumsum}}\left( {2r\left( {{t_1}} \right) - 1} \right),{\rm{cumsum}},} \right.\\ \;\;\;\;\left. {\left( {2r\left( {{t_2}} \right) - 1} \right), \cdots ,{\rm{cumsum}}\left( {2r\left( {{t_n}} \right) - 1} \right)} \right] \end{array} $ | (1) |
式中:cumsum为计算数组累,n为蚂蚁的数目,t为目前的迭代次数,r(t)的表达式为
| $ r\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {1,\;\;\;\;\;{\rm{if}}\;m > {\rm{0}}.{\rm{5}};}\\ {0,\;\;\;\;{\rm{if}}\;m \le {\rm{0}}.{\rm{5}}.} \end{array}} \right. $ | (2) |
式中m为0~1之间的随机数.
蚂蚁的随机游走受到蚁狮的影响,数学表式为
| $ \mathit{\boldsymbol{c}}_i^t = \mathit{\boldsymbol{Y}}_i^t + {\mathit{\boldsymbol{c}}^t}, $ | (3) |
| $ \mathit{\boldsymbol{d}}_i^t = \mathit{\boldsymbol{Y}}_i^t + {\mathit{\boldsymbol{d}}^t}. $ | (4) |
式中:ct为所有变量第t次迭代的最小值,dt为所有变量第t次迭代的最大值,Yit为被选出的第i只蚁狮第t次迭代后的位置.
当蚂蚁在陷阱周围随机移动时,蚁狮会继续挖洞,使蚂蚁慢慢移向自己,数学表式为
| $ {\mathit{\boldsymbol{c}}^t} = \frac{{{\mathit{\boldsymbol{c}}^t}}}{{{{10}^w}\frac{t}{{{T_{\max }}}}}}, $ | (5) |
| $ {\mathit{\boldsymbol{d}}^t} = \frac{{{\mathit{\boldsymbol{d}}^t}}}{{{{10}^w}\frac{t}{{{T_{\max }}}}}}. $ | (6) |
式中:t为当前迭代次数,Tmax为最大的迭代次数,w为固定值,能够调整蚂蚁移向蚁狮的速度,数学表式为
| $ w = \left\{ \begin{array}{l} 2,\;\;\;t > 0.1T;\\ 3,\;\;\;t > 0.5T;\\ 4,\;\;\;t > 0.75T;\\ 5,\;\;\;t > 0.9T;\\ 6,\;\;\;t > 0.95T. \end{array} \right. $ | (7) |
为保证蚂蚁在搜索空间内随机游走,使用式(8)处理
| $ \mathit{\boldsymbol{X}}_i^t = \frac{{\left( {\mathit{\boldsymbol{X}}_i^t - {\mathit{\boldsymbol{a}}_i}} \right) \times \left( {\mathit{\boldsymbol{d}}_i^t - \mathit{\boldsymbol{c}}_i^t} \right)}}{{{\mathit{\boldsymbol{b}}_i} - {\mathit{\boldsymbol{a}}_i}}} + \mathit{\boldsymbol{c}}_i^t. $ | (8) |
式中:ai和bi分别为第i维变量随意游走的最小值和最大值,cit和dit分别为第i维变量第t次迭代的最小值和最大值.
蚂蚁当前的位置为
| $ \mathit{\boldsymbol{B}}_i^t = \frac{{{\mathit{\boldsymbol{A}}^t} + {\mathit{\boldsymbol{E}}^t}}}{2}. $ | (9) |
式中:At为第t次迭代在通过轮盘赌方式选择的蚁狮周围随机游走,Et为第t次迭代在精英蚁狮周围随机游走.
蚁狮捕到Ant后,位置的数学表示
| $ \mathit{\boldsymbol{Y}}_i^t = \mathit{\boldsymbol{B}}_i^t{\rm{if}}\;f\left( {\mathit{\boldsymbol{B}}_i^t} \right) > f\left( {\mathit{\boldsymbol{Y}}_i^t} \right). $ | (10) |
ALO算法步骤如下:
步骤1 设置参数:最大迭代次数Imax、蚂蚁和蚁狮的数目NumB、NumY、适应度函数维数dim以及变量范围u和l.
步骤2 随机初始化蚂蚁和蚁狮的位置,计算相应的适应度值并排序,选出其中适应度值最大的蚁狮作为精英蚁狮个体EAntlion,I=1.
步骤3 通过轮盘赌方式对蚁狮进行贪婪选择,利用式(3)和(4)更新cit和dit的值,实现蚂蚁在选择出的蚁狮和精英蚁狮周围随机游走,利用式(5)~(8)使蚂蚁不断靠近蚁狮,之后根据式(9)更新蚂蚁的位置.
步骤4 游走后的蚂蚁根据式(10)与当前位置最好的蚁狮对比,重新调整最佳蚁狮的位置.如果蚁狮的位置超出了最远边界u或者l,则按照最远边界处理,I=I+1.
步骤5 判断是否达到算法的最大迭代次数或精度,若达到,则获得最佳蚁狮位置,否则转至步骤3.
2 自适应Tent混沌搜索的蚁狮优化算法 2.1 Tent混沌序列Tent混沌方法具备随机性、均匀性和有序性等优势,利用其寻求最优解,可提高种群多样性,取得全局最优解.因此,本文使用Tent混沌序列初始化种群.
Tent映射表达式如下:
| $ {\mathit{\boldsymbol{x}}_{t + 1}} = \left\{ \begin{array}{l} 2{\mathit{\boldsymbol{x}}_t},\;\;\;\;\;\;\;\;\;\;\;0 \le {\mathit{\boldsymbol{x}}_t} \le 0.5;\\ 2\left( {1 - {\mathit{\boldsymbol{x}}_t}} \right),\;\;\;\;0.5 \le {\mathit{\boldsymbol{x}}_t} \le 1. \end{array} \right. $ | (11) |
经过贝努力移位变换后为
| $ {\mathit{\boldsymbol{x}}_{t + 1}} = \left( {2{\mathit{\boldsymbol{x}}_t}} \right)\bmod 1. $ | (12) |
在可行解中生成Tent混沌序列的方式为
步骤1 产生(0, 1)之间的随机数x0作为初值(避免x0在小周期内(0.2, 0.4, 0.6, 0.8)),z(1)=x0,i=j=1;
步骤2 根据式(12)迭代,生成 x(i+1),i=i+1;
步骤3 如果x(i)={0, 0.25, 0.5, 0.75},或x(i)= x(i-k),k={0, 1, 2, 3, 4},按式x(i)= z(j+1)= z(j)+ε改变迭代初值,ε为随机数,j=j+1,否则转向步骤2.
步骤4 若到达最大迭代数,程序结束,保持x序列,否则转到步骤2.
2.2 自适应Tent混沌搜索使用自适应动态调整混沌搜索策略为适应度较差的蚂蚁和蚁狮个体产生适应度较好的新解,改善种群的整体性能.即在每一次迭代中,分别求出种群第j维的最小值Xminj和最大值Xmaxj作为混沌搜索空间,以目前为止搜索到最优值为基础产生Tent混沌序列.主要步骤如下:
步骤1 xk归一化处理
| $ \mathit{\boldsymbol{z}}_k^j\left( 0 \right) = \frac{{\left( {\mathit{\boldsymbol{x}}_k^j - \mathit{\boldsymbol{X}}_{\min }^j} \right)}}{{\left( {\mathit{\boldsymbol{X}}_{\max }^j - \mathit{\boldsymbol{X}}_{\min }^j} \right)}}. $ | (13) |
式中k=1, …, n, j=1, …, D.
步骤2 利用式(12)生成混沌解zkj(m),同时利用式(14)使 zkj(m)还原到解空间的邻域内
| $ \mathit{\boldsymbol{y}}_k^j = \mathit{\boldsymbol{x}}_k^j + \frac{{\left( {\mathit{\boldsymbol{X}}_{\max }^j - \mathit{\boldsymbol{X}}_{\min }^j} \right)}}{2} \times \left( {2\mathit{\boldsymbol{z}}_k^j\left( m \right) - 1} \right). $ | (14) |
步骤3 计算新的适应度值和原值比对,保留更好的解.
步骤4 如果到达最大迭代次数,程序终止,否则转向步骤2.
2.3 锦标赛选择方法基本ALO算法使用轮盘赌法将适应度值占总适应度值的比例作为选择概率选出被学习的蚁狮,使得蚂蚁向适应度高的蚁狮群体集中,破坏了种群多样性,使结果出现早熟收敛,得到局部极值.锦标赛选择机制[7]是从局部竞争机制中产生的,通过随机选取q个个体进行比较,从中选取适应度值较大者作为最优个体.本文采用锦标赛策略选取被学习蚁狮个体,并使q =2.在每次选取的过程中,奖励适应度值大的1分,重复n次,其中得分最高的权重也最大.由于锦标赛选择策略使用适应度的相对值作为选择标准,并且未对适应度值正负做要求,进而避免了超级个体对进化过程的影响.适应度选择概率为
| $ {P_i} = \frac{{{c_i}\left( t \right)}}{{\sum\limits_{i = 1}^N {{c_i}\left( t \right)} }}. $ | (15) |
式中ci为每个个体得分.
2.4 Logistic混沌搜索将典型的Logistic混沌算子与蚂蚁随意行为结合成混沌蚁群,使蚂蚁能够全局寻优,改善了算法取得全局最优值的性能.混沌变量数学表达式为[9]
| $ {x_{n + 1}} = 4{x_n}\left( {1 - {x_n}} \right). $ | (16) |
式中xn是0~1之间的一个随机数.
经过改进,可将混沌蚂蚁的全局搜索能力和蚁狮的局部搜索能力结合,改善了算法的整体收敛时间和精度.
2.5 自适应Tent混沌搜索的蚁狮算法流程算法的步骤如下:
步骤1 设置参数:蚁狮算法的最大迭代次数Imax、蚂蚁和蚁狮的数目NumB和NumY、适应度函数维数dim、变量范围u和l以及混沌策略的最大迭代次数m.
步骤2 在搜索区域内,利用Tent混沌序列优化种群,分别生成NumB和NumY个dim维向量 Xi,I=1.
1.随机生成NumB和NumY个(0, 1)之间dim维向量 ZiD(t),根据Tent混沌序列可得相应的序列 ZiD(t).
2.利用式(17)将 ZiD(t)载波到对应变量的取值范围内,即
| $ \mathit{\boldsymbol{X}}_j^i\left( t \right) = \mathit{\boldsymbol{X}}_{\min }^j + \left( {\mathit{\boldsymbol{X}}_{\max }^j - \mathit{\boldsymbol{X}}_{\min }^j} \right)\mathit{\boldsymbol{z}}_i^j\left( t \right). $ | (17) |
步骤3 利用自适应Tent混沌搜索为种群中适应度较差蚂蚁和蚁狮产生新解.
1.设置参数:种群中较差个体比例p0,选出个数是p0×Num,Tent混沌搜索次数是n.
2.自适应Tent动态调整混沌搜索空间方法为p0×Num个个体产生新解.
步骤4 计算 Xi适应度值并排序,从中选出值最大的个体作为精英个体EAntlion.
步骤5 通过锦标赛选择方式对蚁狮进行选择,并更新 cit和 dit的值.
步骤6 将混沌算子与蚂蚁的随机游走相结合,利用式(3)和(4)实现蚂蚁在蚁狮周围混沌随机游走,利用式(5)~(8)使蚂蚁不断靠近蚁狮,之后根据式(9)更新蚂蚁的位置.
步骤7 游走后的蚂蚁根据式(10)与当前位置最好的蚁狮对比,重新调整最佳蚁狮的位置.如果蚁狮的位置超出了最远边界u或者l,则按照最远边界处理,I=I+1.
步骤8 判断是否达到算法的最大迭代数,若达到,则输出最佳蚁狮位置,否则回到步骤3.
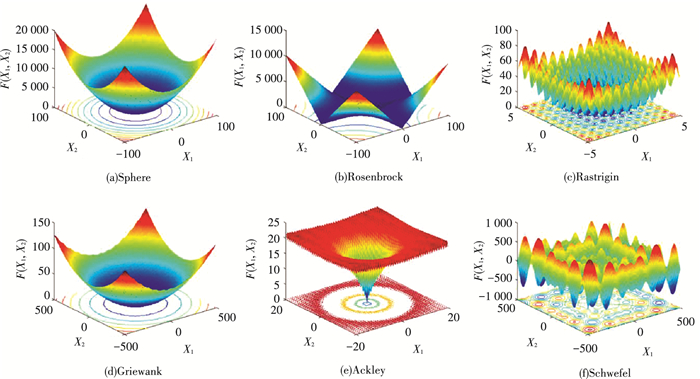
3 仿真实验与结果分析 3.1 基准测试函数为验证提出的SATC-ALO算法的特性, 选取了6个Benchmark基准函数[10]和航迹规划问题对算法进行寻优测试.其中,基准函数的不同性能可以充分检验算法的性能,见表 1所示.单峰函数主要检验其寻优性能和收敛速度,复杂非线性多峰函数主要检验算法的全局优化能力、跳出局部最优值等性能.航迹规划问题可以检验SATC-ALO算法在具体问题上的实时性和准确性.实验仿真环境为Inter(R) Core(TM) i5-6500, CPU, 3.20GHz, 4GB RAM, Win7操作系统,仿真软件为MATLAB R2014a.
| 表 1 基准测试函数 Table 1 Benchmark functions |
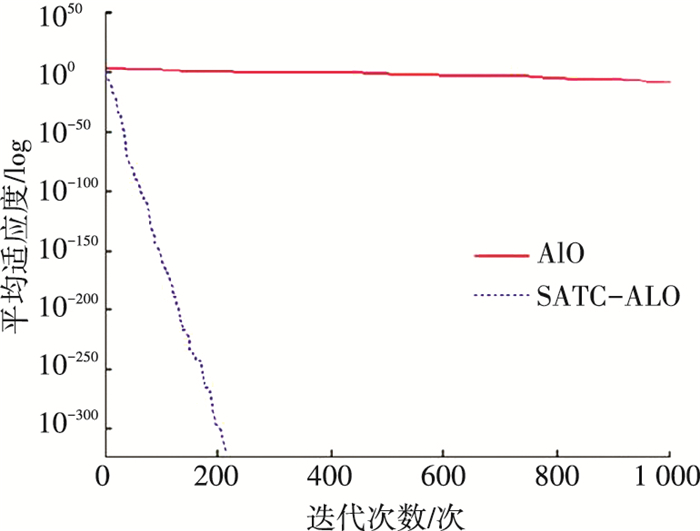
为了评价算法效用性,采用ALO和SATC-ALO算法进行测试.实验参数设置:蚂蚁和蚁狮的个数为100个,最大迭代次数为1 000次,种群中较差个体比例p0为0.3,混沌搜索次数为30次.通过对比每个测试函数运行50次得到的适应度平均值、方差等参数来评价各个算法的优化能力. 30维基准测试函数进化曲线见图 2~7所示,30维和50维的测试结果见表 2所示.
|
图 2 Sphere函数动态寻优过程(30维) Figure 2 The progress curve of Sphere function (30 dimensions) |

|
图 3 Rosenbrock函数动态寻优过程(30维) Figure 3 The progress curve of Rosenbrock function (30 dimensions) |

|
图 4 Rastrigin函数动态寻优过程(30维) Figure 4 The progress curve of Rastrigin function (30 dimensions) |

|
图 5 Griewank函数动态寻优过程(30维) Figure 5 The progress curve of Griewank function (30 dimensions) |
|
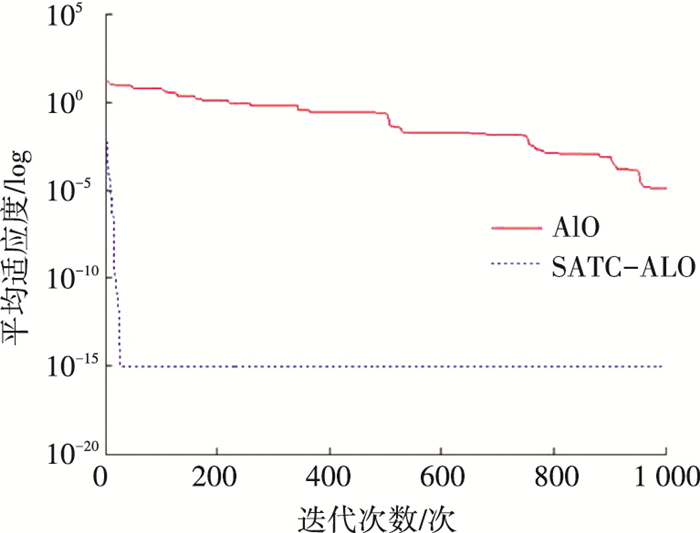
图 6 Ackley函数动态寻优过程(30维) Figure 6 The progress curve of Ackley function (30 dimensions) |
|
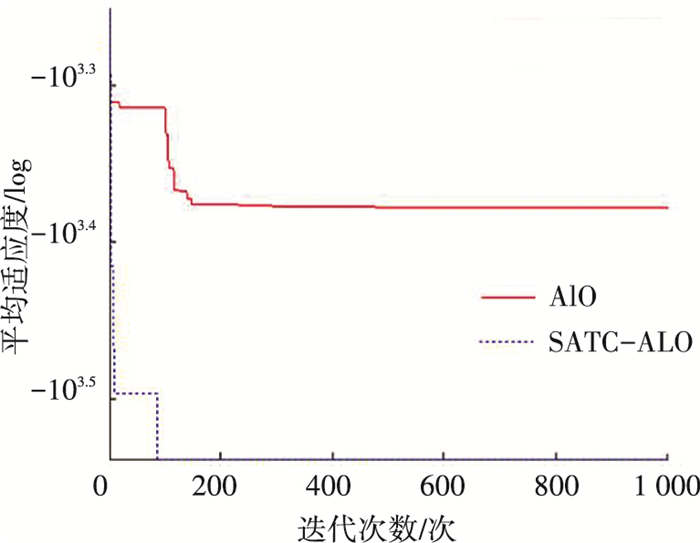
图 7 Schwefel函数动态寻优过程(30维) Figure 7 The progress curve of Schwefel function (30 dimensions) |
| 表 2 基准函数的优化结果比较 Table 2 Optimization results comparison of benchmark functions |
由图 2~6和表 2可知,无论是针对单峰函数还是针对多峰函数,SATC-ALO算法的收敛时间均明显优于ALO算法,全局寻优效果好,可以连续、高效地搜寻到函数最小值.由图 7和表 2可知,对多峰函数Schwefel,取值范围为[-500, 500],最优值在搜索空间边界附近,使算法极易陷入到某一个局部最优解之中,但SATC-ALO算法收敛值接近理论最优值,并且寻优速度也明显优于ALO算法.
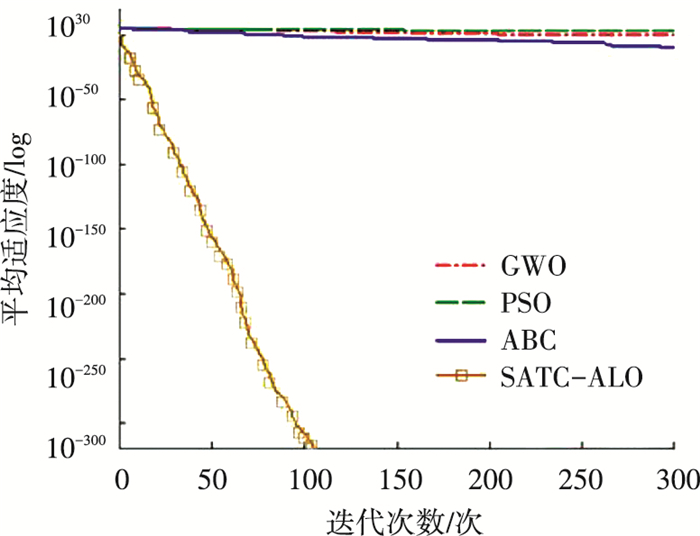
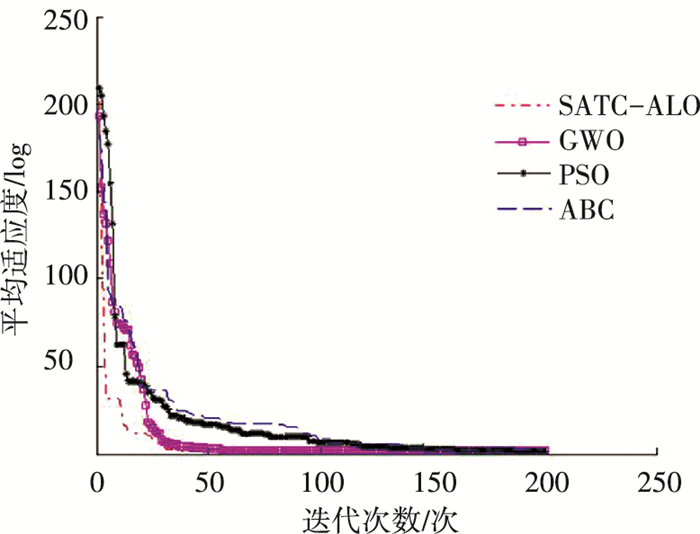
进一步验证SATC-ALO算法的优越性,将其与智能算法中寻优能力较好的人工蜂群算法(ABC)[11],粒子群算法(PSO)[12],灰狼算法(GWO)[13]进行了比较,选择Sphere函数和Griewank函数作为测试函数,设置函数维度为50,最大迭代次数为300次. 4种算法对两种测试函数寻优的进化过程见图 8~9所示.基准函数的搜索区域见图 10所示.
|
图 8 Sphere函数动态寻优过程(50维) Figure 8 The progress curve of Sphere function (50 dimensions) |
|
图 9 Griewank函数动态寻优过程(50维) Figure 9 The progress curve of Griewank function (50 dimensions) |
|
图 10 基准函数的搜索区域 Figure 10 Search space of benchmark functions |
由图 8~9和表 2可知,对于Sphere函数和Griewank函数,SATC-ALO算法的收敛精度和时间均明显好于其他三种智能算法.
综上所述,在收敛速度和寻优精度上,SATC-ALO算法较ALO算法和大部分智能算法均有明显的提升,具有较好的全局优化和跳出局部最优的能力,并且鲁棒性较好.
3.2.2 航迹规划问题性能分析作为一种新型高效的群智能算法,SATC-ALO算法可以应用在许多工程领域,比如航迹规划、火力分配问题以及其他寻优问题.以无人机航行轨迹规划问题为例介绍SATC-ALO算法的具体用法并测试其应用性能.
航迹规划问题主要考虑油耗和威胁指标,表达式为
| $ {J_t} = \int_0^L {{w_t}{\rm{d}}l} . $ | (18) |
| $ {J_f} = \int_0^L {{w_f}{\rm{d}}l} . $ | (19) |
式中:wt和wf分别为航迹点的威胁代价和油耗代价,L为整段航迹的长度.将整段航迹平均分成10段,计算奇数分点的评价指标.因此,威胁代价为
| $ \begin{array}{l} {w_{t,{L_i}}} = \frac{{{L_i}}}{5} \cdot \sum\limits_{k = 1}^N {{t_k} \cdot \left( {\frac{1}{{d_{0.1,i,k}^4}} + \frac{1}{{d_{0.3,i,k}^4}} + \frac{1}{{d_{0.5,i,k}^4}} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{{d_{0.7,i,k}^4}} + \frac{1}{{d_{0.9,i,k}^4}}} \right) \end{array} $ | (20) |
式中:N为威胁源的数目; tk为常数,由具体威胁源决定; Li为第i段航迹的长度; d0.1, i, k4为1/10点与威胁源k之间的距离.总的航迹代价为[8]
| $ J = k{J_t} + \left( {1 - k} \right){J_f}. $ | (21) |
式中k为威胁权值,根据具体情况取值.
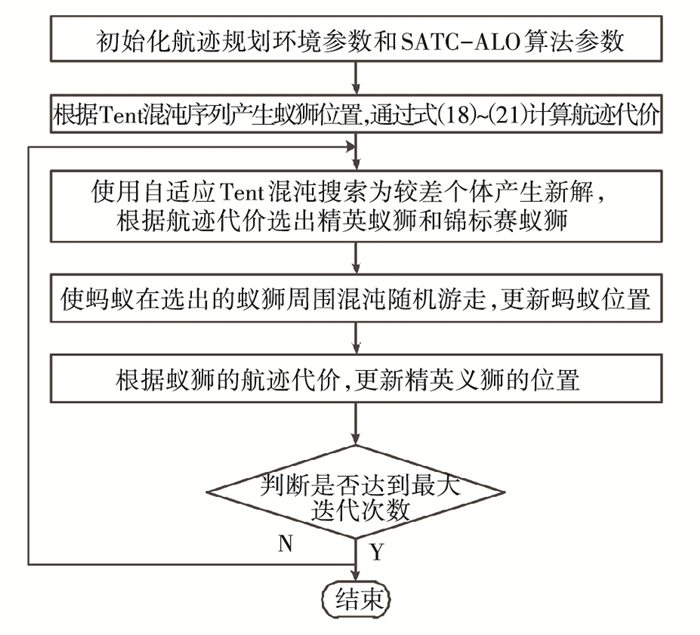
SATC-ALO解决航迹规划问题的流程图见图 11.
|
图 11 航迹规划算法流程图 Figure 11 The flow diagram of path planning |
仿真实验:设置无人机的起点坐标为(10 km, 10 km),目标点坐标为(100 km, 75 km),具体的威胁源分布见表 3所示.设置种群规模为15,Tmax为150,D为10. SATC-ALO算法得到的航迹仿真结果见图 12、13.
| 表 3 威胁源信息 Table 3 Information of threat source |
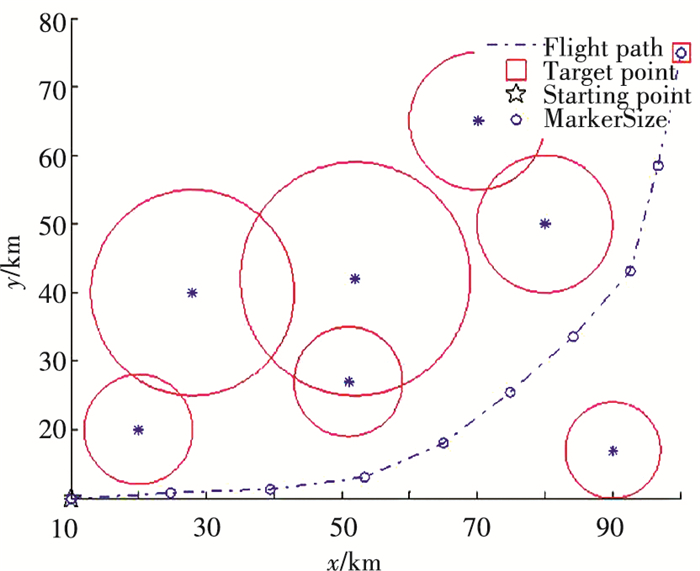
|
图 12 SATC-ALO算法规划的航迹 Figure 12 Path planning result optimized by SATC-ALO algorithm |
|
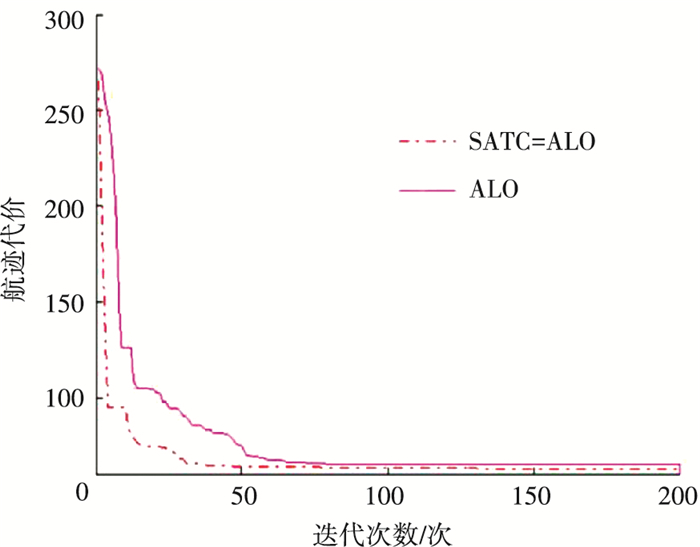
图 13 航迹代价收敛曲线 Figure 13 Convergence curves of algorithms |
仿真结果表明,SATC-ALO算法经过0.939秒,迭代30次基本可以达到航迹代价最优值,满足实时性条件.由图 12和图 13可知,在航迹规划问题上,SATC-ALO算法的收敛速度和精度均优于ALO算法,可快速准确规划出一条满足要求的航迹,具有实际应用价值.
4 结论本文提出了自适应Tent混沌搜索的蚁狮优化算法(SATC-ALO).主要从如下4个方面对ALO算法进行了优化:1)引入Tent混沌搜索优化种群,获得遍历均匀的个体,提升其多样性; 2)自适应动态调整Tent混沌搜索空间,将混沌算子与蚂蚁的随机游走结合,使蚂蚁能够进行混沌搜索,提高算法跳出局部最优解的能力; 3)利用Tent混沌搜索为种群中适应度较差蚂蚁和蚁狮产生新解,避免算法陷入局部最优值; 4)使用锦标赛选择策略取代轮盘赌方式选择蚁狮,较为有效地规避了算法早熟收敛以及出现超级个体的现象.
对6个标准函数和航迹规划问题进行寻优测试.实验结果表明,SATC-ALO算法在保证种群均匀性和多样性的前提下,能够尽量避免早熟和陷入局部最优问题,具有优秀的收敛速度和寻优精度,并且算法相对稳定,鲁棒性较好.
| [1] |
MIRJALILI S. The ant lion optimizer[J].
Advances in Engineering Software, 2015, 83(C): 80-98.
DOI: 10.1016/j.advengsoft.2015.01.010 |
| [2] |
罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[J].
控制与决策, 2010, 25(12): 1913-1916.
LUO Jun, LI Yan. Artificial bee colony algorithm with chaotic search strategy[J]. Control and Decision, 2010, 25(12): 1913-1916. DOI: 10.13195/j.cd.2010.12.156.luoj.013 |
| [3] |
GAO W F, LIU S Y. A modified artificial bee colony algorithm[J].
Computer & Operations Research, 2012, 39(3): 687-697.
|
| [4] |
匡芳君, 金忠, 徐蔚鸿, 等. Tent混沌人工蜂群与粒子群混合算法[J].
控制与决策, 2014, 31(11): 1502-1508.
KUANG Fangjun, JIN Zhong, XU Weihong, et al. Artificial bee colony algorithm based on self-adaptive tent chaos search[J]. Control Theory & Applications, 2014, 31(11): 1502-1508. DOI: 10.13195/j.kzyjc.2014.0750 |
| [5] |
匡芳君, 徐蔚鸿, 金忠. 自适应Tent混沌搜索的人工蜂群算法[J].
控制理论与应用, 2015, 30(5): 839-847.
KUANG Fangjun, XU Weihong, JIN Zhong. Hybridization algorithm of Tent chaos artificial bee colony and particle swarm optimization[J]. Control and Decision, 2015, 30(5): 839-847. DOI: 10.7641/CTA.2014.31114 |
| [6] |
AKAY B, KARABOGA D. A modified artificial bee colony algorithm for real-parameter optimization[J].
Information Sciences, 2012, 192(6): 120-142.
DOI: 10.1016/j.ins.2010.07.015 |
| [7] |
BAO L, ZENG J C. Comparison and analysis of the selection mechanism in the artificial bee colony algorithm[C]//2009 9th International Conference on Hybrid Intelligent Systems. Los Alamitos, CA: IEEE, 2009: 411-416. DOI: 10.1109/his.2009.319.
|
| [8] |
XU C F, DUAN H B, LIU F. Chaotic artificial bee colony approach to uninhabited combat air vehicle (UCAV) path planning[J].
Aerospace Science and Technology, 2010, 14(8): 535-541.
DOI: 10.1016/j.ast.2010.04.008 |
| [9] |
ALATAS B. Chaotic bee colony algorithms for global numerical optimization[J].
Expert Systems with Applications, 2010, 37(8): 5682-5687.
DOI: 10.1016/j.eswa.2010.02.042 |
| [10] |
LIAO X, ZHOU J Z, OUYANG S, et al. An adaptive chaotic artificial bee colony algorithm for short-term hydrothermal generation scheduling[J].
Electrical Power and Energy Systems, 2013, 53(12): 34-42.
DOI: 10.1016/j.ijepes.2013.04.004 |
| [11] |
Pan T S, Dao T K, Pan J S, et al. An unmanned aerial vehicle optimal route planning based on compact artificial bee colony[C]//Advances in Intelligent Information Hiding and Multimedia Signal Processing (IHMS). Kaohsiung, Taiwan, Springer, 2016: 361-369. DOI: 10.1007/978-3-319-50212-0_43.
|
| [12] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks(ICNN). Piscataway, NJ: IEEE Press, 1995: 1942-1948.
|
| [13] |
MIRJALILI S, MIRJALILI SM, LEWIS A. Grey wolf optimizer[J].
Advances in Engineering Software, 2014, 69: 46-61.
DOI: 10.1016/j.ins.2014.09.011 |
 2018, Vol. 50
2018, Vol. 50


