在纳米尺度中,多晶材料的晶粒可分为晶粒内部(3维)、晶界面(2维)、三叉晶界(1维)和顶点团(0维)等结构[1-2],这些微观结构的能量、力学特性、配位度等因素直接影响多晶材料的加工性能.国内外学者对多晶材料纳米加工过程的作用机理、错配位错的呈核、生长、滑移以及力学特性进行了大量研究[3-8].在纳米尺度多晶材料加工机理的研究中,纳米压痕是一种快速高效的实验方法,采用金刚石探针对金属表面不同位置进行压痕,获得探针的压痕力-压痕深度曲线,对比不同位置压痕力曲线的趋势以获得材料基体力学特性的分布规律.其中,材料表层及亚表层位错的分布情况对加工后材料的强度、硬度及表面粗糙度有较大的影响[9-10],因此研究材料压痕表面位错的成核及衍生规律具有较高的实用价值.
国内外研究者也关注多晶铜晶粒的尺寸效应、霍尔效应在多晶铜压痕实验中对材料特性的影响机制,如Hou等[11]对不同晶粒度的多晶铜表面进行压痕实验,分析了压痕力与晶粒度之间的霍尔效应和反霍尔效应,并提出一种新的用于预测探针压痕力的预测函数; Ma等[12]基于压痕实验对单晶铜和多晶铜纳米压痕后的材料强度进行了对比,发现多晶铜材料强度优于单晶铜强度.近年来,随着微/纳机电系统制造技术的发展,纳米压痕已成为纳米加工中不可或缺的加工方法,而对多晶材料微观结构纳米压痕机理的实验研究仍存在大量空白.分子动力学(Molecular Dynamics,简记为MD)方法能够模拟探针与材料间原子尺度的作用过程,分析位错的成核及扩展规律并提供压痕过程中全部原子的瞬态信息,进而详细地获取材料的变形机理.目前,纳米压痕的分子动力学模拟计算对象主要为单晶铜,且建立的多晶材料模型并未对多晶材料的微观结构进行辨识.
本文通过Poisson-Voronoi和Monte Carlo方法建立大尺度金刚石探针-多晶铜纳米压痕分子动力学模型,并对多晶铜的各个微观结构进行辨识.多晶铜的晶粒内部原子呈各向同性排布,晶粒间原子呈各向异性排布,而晶界原子呈过渡态无序排布,导致多晶铜的晶粒与晶界具有不同的力学特性.此外晶界所具有的晶界面、三叉晶界和顶点团等微观结构的力学特性也具有较大差异.因此,本文研究了探针初始压痕位置分别位于多晶铜表面各微观结构时对多晶铜纳米压痕机理的影响.研究探针压痕力及多晶铜内应力的演化规律,并对多晶铜亚表层错配位错的成核及衍生过程进行了分析,为多晶材料的纳米加工机理提供一些理论依据.
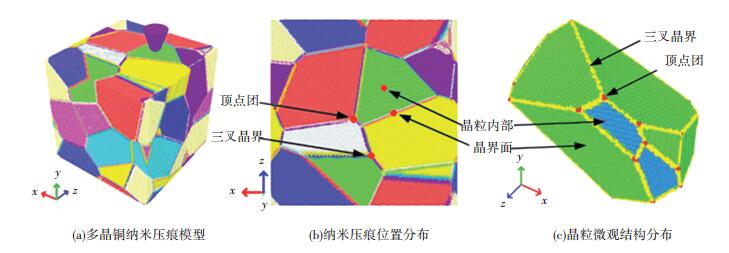
1 建模与模拟 1.1 模型的建立图 1为采用Poisson-Voronoi和Monte Carlo法建立的多晶铜纳米压痕分子动力学模型,具体细节可参考文献[13-15]. 图 1(a)为多晶铜纳米压痕模型,多晶铜模型尺寸为45 nm×45 nm×45 nm的正四面体,平均晶粒度为21.37 nm,含铜原子数为614万.由于金刚石具有良好的硬度、导热系数、刃口的成形性,压痕压头材料采用金刚石(晶格常数为0.357 nm),其外形为扫描探针结构. 图 1(b)为多晶铜模型沿Y轴方向的俯视图,图中箭头标记为探针初始压痕位置,分别为晶粒内部、晶界面、三叉晶界及顶点团. 图 1(c)为多晶铜模型中单个晶粒的三维视图,为便于观察晶粒内部原子,将其中两个晶界面隐藏,采用箭头分别标记该晶粒的4类微观结构.
|
图 1 多晶铜纳米压痕分子动力学模型 Figure 1 Polycrystalline copper nanoindentation molecular dynamics model |
为研究压痕位置对多晶铜变形机理的影响,对压痕位于4类微观结构的纳米压痕分子动力学模型分别进行了模拟计算,采用的方法如下:多晶铜采用周期性边界条件,探针初始位置位于多晶铜各个微观结构表面上方0.5 nm处,以确保探针原子与多晶铜原子距离大于自由程.同时,模型Y轴方向整体受力设定为零,使模型底层原子能够平衡上层原子受到的压痕力,确保探针运动过程中多晶铜整体不发生运动.采用共轭梯度法进行能量最小化并在NPT系综弛豫,弛豫时间为50 ps.系统外界压力设定为0,系统模型温度设定为10 K,使模型在较快速度下结晶,消除多晶铜内部非平衡态原子.探针设定为理想化刚性模型,即在压痕过程中,探针模型结构不在力的作用下发生改变. EAM势被用于描述铜原子间相互作用,Morse势被用于描述金刚石与铜之间的相互作用.探针压入多晶铜是对其稳定的面心立方(face-centered cubic,简记为FCC)晶体结构的破坏过程,位错形核并滑移,破坏多晶铜原有的稳定状态.为探究晶界等微观结构和晶粒在压痕过程中原子的运动规律及其差异,对多晶铜的不同微观结构进行压痕模拟计算.采用中心对称参数(center-symmetry parameter,简记为CSP)法分析多晶铜在纳米压痕过程中位错的形核及扩散规律.此外, 分别采用静应力(hydrostatic pressure,简记为HY)和第三应力(von mises stress,简记为VM)分析多晶铜在压痕过程中的应力分布. 表 1为多晶铜纳米压痕模拟计算的模型参数.
| 表 1 多晶铜纳米压痕中使用的MD模拟计算参数 Table 1 The MD simulation parameters for polycrystalline copper nanoindentation |
图 2为初始压痕位置为各类微观结构时多晶铜的压痕深度-压痕力曲线.由图 2可知,多晶铜纳米压痕的压痕力为纳牛级,且压痕力与压痕深度呈近似线性增长关系,与压痕方向Y正交的X和Z方向压痕力变化不明显.当压痕深度<0.15 nm时,压痕力变化较小,这是由于压痕过程处于弹性变形阶段,晶粒原子通过调整晶格点阵位置以平衡压痕过程累积的应变量;随着压痕深度的继续增大,压痕力线性增大,在压痕深度为0.15 nm时刻压力曲线第一次产生拐点,说明压痕深度为0.15 nm时,应变到达多晶体的屈服极限位置,此时多晶铜的变形过程由之前的弹性变形转变为塑性变形,多晶铜处于塑性变形阶段.该多晶铜模型的纳米压痕力曲线趋势与文献[11]一致,而压痕力大小略有不同,这主要是由于多晶铜晶粒度大小差异引起的.

|
图 2 不同压痕位置多晶铜压痕深度-压痕力曲线 Figure 2 Indentation force-indentation depth curves with different initial nanoindentaiton position |
在塑性变形阶段,压痕深度-压痕力曲线具有显著波动,这是由于多晶铜塑性变形过程伴随着位错、堆垛层错等缺陷的形核与扩展,同时伴随着内应力和原子势能不断累积与释放,多种因素导致了压痕塑性变形阶段力曲线的波动.为了更好地对比初始压痕位置对探针压痕力大小的影响,将初始压痕位置分别位于4种微观结构的Y方向压痕力曲线进行对比,发现压痕深度-压痕力曲线斜率关系为:晶粒内部>晶界面>三叉晶界>顶点团,这表明压痕位于晶粒内部时,探针受压痕力最大,而压痕位于顶点团时,探针受到压痕力最小.
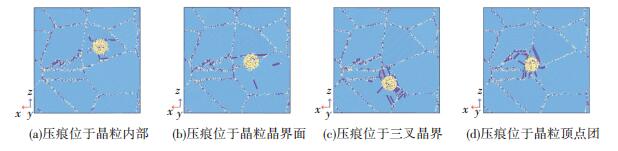
2.2 压痕位置对缺陷分布范围的影响图 3为初始压痕位置分别位于多晶铜表面各个微观结构时,多晶铜表面的缺陷分布,其中探针未显示以便于观察多晶铜表面的缺陷分布.通过跟踪压痕过程中多晶铜缺陷的形核及扩展过程,表明缺陷结构主要包括CSP为0的不完全位错和CSP为3的位错层结构. 图 3表明对多晶铜表面不同微观结构位置压痕得到的表面位错分布具有显著差异.对比模拟的压痕表面与文献[11]的实验结果发现,多晶铜模型压痕表面结构与多晶铜实验观察现象相同.此外,实验中压痕局部发生形状恢复,这主要是由于压痕位置内部的残余应力释放引起的弹性变形,这与仿真模拟中探针离开多晶铜表面后弛豫的结果一致.
|
图 3 多晶铜纳米压痕内缺陷结构 Figure 3 Internal defect structure of polycrystalline copper nanoindentation surface |
当压痕位于晶粒内部时,位错滑移运动被该晶粒的晶界束缚,最终被限制在单一晶粒内部; 当压痕位于晶界(包括晶界面、三叉晶界、顶点团)等微观结构时,位错同时存于共同拥有该晶界的多个晶粒内部.因此,多晶铜晶界位置压痕产生的位错分布范围远大于晶粒内部压痕产生的位错分布范围.这主要是由于在金刚石探针压入多晶铜晶粒时,针尖的碳原子与多晶铜原子间产生剧烈的挤压,在针尖碳原子压应力的作用下,多晶铜原子由FCC晶体结构转变为具有HCP晶体结构的缺陷原子.位于探针正下方的铜原子变化最为剧烈,形成大量的不完全位错及堆垛层等缺陷.随着探针的压痕深度增大,位错等缺陷结构不断扩展.与晶粒内部不同,晶界被多个晶粒所共有,压痕过程中压痕力将同时作用于多个晶粒,因此压痕位于晶界使多晶铜表面位错分布范围显著增大.
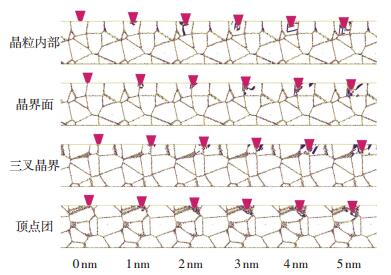
复杂的晶界网络导致压痕位错分布难以完整可视化,截取多晶铜模型压痕位置切片,隐藏多晶铜晶粒全部FCC结构原子,得到多晶铜纳米压痕过程内部缺陷分布截面,如图 4所示,分别为初始压痕位于4种微观结构时多晶铜表面位错的演化过程.
|
图 4 初始压痕位置-压痕深度系统原子结构示意(FCC铜原子未显示) Figure 4 Initial indentation location-indentation depth atomic structure model, FCC copper atoms are hiddenned |
当压痕位于晶粒内部时,起始时刻多晶铜晶粒内部无位错缺陷,随着晶粒应变量增大铜原子受到压应力不断增大且伴随着原子势能不断累积,位错首先在针尖正下方晶粒内部成核,并沿位错滑移面在晶粒内部不断扩展.当晶粒内位错层运动至相邻晶粒面时,晶粒间的晶界结构阻碍位错的进一步滑移,将位错约束在同一晶粒内部.当压痕位于晶界(包括晶界面、三叉晶界、顶点团)时, 多晶铜晶界位置受到探针的压痕力而产生位错变形,这时由于晶界位置的弹性较弱,不存在明显的弹性变形阶段.
随后位错在晶界位置大量成核并沿滑移面向晶界相邻晶粒内部不断扩展.此时,由于压痕位于多个晶粒共有的晶界面处,位错同时在多个晶粒内部产生位错层滑移现象.而当压痕位于晶粒内部时,只有当压痕深度继续增大至晶界结构无法承载内应力时,位错层才会穿越晶界面扩展至相邻晶粒中.对比不同压痕位置模拟计算结果可知, 缺陷结构主要产生于探针正下方的局部铜原子,压痕位于晶粒内部会在较少的晶粒内部产生缺陷结构,而压痕位于晶界面会同时在多个晶粒内部产生大量位错缺陷.文献[12]的实验结果与本工作的仿真模拟结果具有一致性.
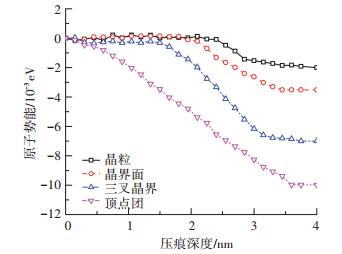
2.3 压痕位置对微观结构的影响对比压痕位于晶粒内部、晶界面、三叉晶界、顶点团各微观结构势能变化规律,发现各微观结构在压痕过程中不断累积能量,平均原子势能显著增大; 压痕位于低维度数微观结构(如三叉晶界顶点团)情况下,各微观结构更易累积能量.如初始压痕位于晶粒或晶界面情况下,压痕深度2.2 nm和2.0 nm时,三叉晶界结构获得显著能量累积,而初始压痕位于三叉晶界或顶点团情况下,压痕深度1.5 nm和0.5 nm时,三叉晶界与顶点团结构就能获得显著能量累积,如图 5所示.
|
图 5 不同初始压痕位置时三叉晶界的能量变化曲线 Figure 5 Initial indentation location-atomic potential energy curves for triple junction |
通过统计多晶铜纳米压痕过程中位错扩展范围内各类微观结构的静应力,并且对比压痕位于晶粒内部、晶界面、三叉晶界、顶点团等微观结构静应力的变化规律,发现压痕过程中各微观结构之间存在显著的相互作用,如图 6所示.当一部分微观结构内应力表现为压应力时,另一部分微观结构表现为拉应力.当高维度数微观结构表现为压应力时,低维度数微观结构更易表现为拉应力; 当低维度数微观结构表现为压应力时,高维度数微观结构更易表现为压应力,如压痕位于晶粒内部时,晶粒微观结构表现为压应力,由于晶粒受到挤压作用发生塑性变形,低维度的三叉晶界、顶点团等微观结构表现为拉应力; 压痕位于三叉晶界的压痕过程中,由于三叉晶界微观结构表现为压应力,压应力向晶界面、晶粒内部等结构传递,而晶体结构的塑性变形使顶点团结构表现为拉应力.
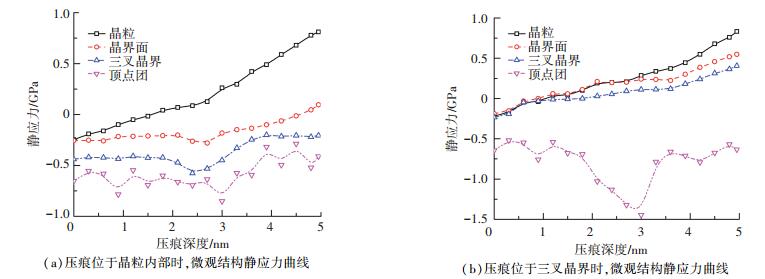
|
图 6 压痕分别位于晶粒内部和三叉晶界的静应力结果 Figure 6 Hydrostatic pressure curves with indentation position respectively located at the grain cell and the triple junction |
这主要由于低维数微观结构被多个高维数微观结构共同拥有,当低维数微观结构受到外力(压力)作用时,作用力将迅速传递至高维数微观结构,使高维数微观结构具有低维数微观结构相同方向的外力(压力).当高维数微观结构受到外力(压力)作用时,作用力将不会直接传递至低维数微观结构,为了平衡高维数微观结构的塑性变形,低维数微观结构将受到反方向的外力(拉力)作用.
图 7为多晶铜纳米压痕过程中晶粒内部原子静应力分布.压痕过程中探针周围铜原子静应力为极大的压应力,与晶粒内部压应力区域相邻区域原子呈拉应力.当压痕深度达1.5 nm时,晶粒的顶点团、三叉晶界原子呈拉应力,图中用圆标记.当压痕深度达2.5 nm时,晶粒的晶界面原子呈拉应力,图中用椭圆标记.当压痕深度达4.5 nm时,最大压应力达56 GPa.
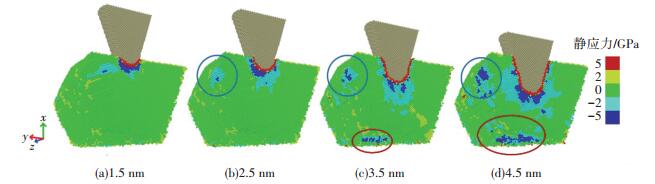
|
图 7 压痕位于晶粒内部时,不同压痕深度下晶粒内部静应力分布 Figure 7 Hydrostatic pressure distribution in grain with nanoindentation position at grain cell for different indentation depth |
图 8为多晶铜纳米压痕过程中晶粒内部原子Von Mises应用分布,根据Von Mises应力分布可知,晶粒内部应力的传递方向是由探针附近向晶界方向传递.与晶界面(2维)相比,应力更易向三叉晶界(1维)、顶点团(0维)等低维数微观结构传递.因此,在纳米压痕过程,位错首先扩展至顶点团与三叉晶界等结构,如图 7(b)所示,进而扩展至晶界面等结构,如图 7(c)(d)所示.即位错和内应力的易扩展方向顺序表现为:顶点团>三叉晶界>晶界面.此外,为保证晶粒受力平衡,晶界将表现为与晶粒内部压应力相反的拉应力.由文献[12]的多晶铜纳米压痕实验结果发现,不同微观结构的纳米压痕反作用力大小与其维度数具有相关性,作用力大小满足:晶粒内部>晶界面>三叉晶界>顶点团.本工作在该实验的基础上,发现晶粒内部原子静应力和Von Mises均满足该数值规律.
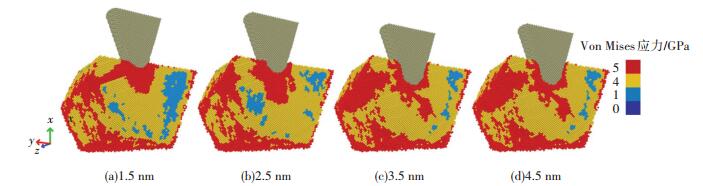
|
图 8 压痕位于晶粒内部时,不同压痕深度下晶粒内部Von Mises应力分布 Figure 8 Von Mises stress distribution in grain with nanoindentation position at grain cell for different indentation depth |
本文模拟了多晶铜表面纳米压痕模拟计算,通过分析多晶铜亚表层缺陷的演化过程、初始压痕分别位于晶粒内部、晶界、三叉晶界和顶点团等微观结构的压痕力-压痕深度曲线、各微观结构原子势能-压痕深度曲线、微观结构原子静应力-压痕深度曲线等,揭示初始压痕位于不同微观结构对多晶铜纳米压痕变形过程中的影响,得到以下结论:
1) 初始压痕位置位于晶界(含晶界面、三叉晶界、顶点团)处更易使多晶铜产生位错等缺陷结构,缺陷会在该晶界的相邻晶粒内部扩散;而压痕位于晶粒内部时,由于受到晶界的束缚,缺陷主要在该晶粒内部成核滑移并终止于晶界面处.
2) 压痕过程中,多晶铜各类微观结构均不断累积能量,且各微观结构累积能量顺序与压痕位置有关;压痕位于高维度数微观结构时,高维度数结构更易累积能量;压痕位于低维度数微观结构时,高维数与低维数微观结构均易累积能量.
3) 多晶材料纳米压痕过程中,当高维度数微观结构表现为压应力时,低维度数微观结构更易表现为拉应力,当低维度数微观结构表现为压应力时,高维度数微观结构更易表现为压应力.
| [1] |
XU T, SARKAR S, LI M, et al. Quantifying microstructures in isotropic grain growth from phase field modeling: Methods[J]. Acta Materialia, 2012, 60(12): 4787-4799. DOI:10.1016/j.actamat.2012.05.040 |
| [2] |
XU T, SARKAR S, LI M, et al. Quantifying microstructures in isotropic grain growth from phase field modeling: Topological properties[J]. Acta Materialia, 2013, 61(7): 2450-2459. DOI:10.1016/j.actamat.2013.01.017 |
| [3] |
WANG F, HUANG P, XU K. Strain rate sensitivity of nanoindentation creep in polycrystalline Al film on Silicon substrate[J]. Surface and Coatings Technology, 2007, 201(9): 5216-5218. DOI:10.1016/j.surfcoat.2006.07.114 |
| [4] |
XU B, YUE Z, WANG J. Indentation fatigue behaviour of polycrystalline copper[J]. Mechanics of Materials, 2007, 39(12): 1066-1080. DOI:10.1016/j.mechmat.2007.06.001 |
| [5] |
XU B, WANG X, YUE Z. Indentation behavior of polycrystalline copper under fatigue-peak overloading[J]. Journal of materials research, 2007, 22(6): 1585-1592. DOI:10.1557/JMR.2007.0201 |
| [6] |
CHAUDHRI M. Subsurface strain distribution around Vickers hardness indentations in annealed polycrystalline copper[J]. Acta Materialia, 1998, 46(9): 3047-3056. DOI:10.1016/S1359-6454(98)00010-X |
| [7] |
CHEN J, SHEN Y, LIU W, et al. Effects of loading rate on development of pile-up during indentation creep of polycrystalline copper[J]. Materials Science and Engineering: A, 2016, 656: 216-221. DOI:10.1016/j.msea.2016.01.042 |
| [8] |
WANG F, XU K. Effect of substrate bias on nanoindentation hardness and microstructure of polycrystalline copper thin films[J]. Rare Metal Materials and Engineering, 2004, 33(5): 531-533. |
| [9] |
LIM Y, CHAUDHRI M. Nanohardness mapping of the curved surface of spherical macroindentations in fully annealed polycrystalline oxygen-free copper[J]. physica status solidi (a), 2002, 194(1): 19-29. DOI:10.1002/1521-396X(200211)194:1<19::AID-PSSA19>3.0.CO;2-I |
| [10] |
XU B, YUE Z F, CHEN X. Numerical investigation of indentation fatigue on polycrystalline copper[J]. Journal of Materials Research, 2009, 24(3): 1007-1015. DOI:10.1557/jmr.2009.0107 |
| [11] |
HOU X, BUSHBY A, JENNETT N. Study of the interaction between the indentation size effect and Hall-Petch effect with spherical indenters on annealed polycrystalline copper[J]. Journal of Physics D: Applied Physics, 2008, 41(7): 074006. DOI:10.1088/0022-3727/41/7/074006 |
| [12] |
MA X, YANG W. Molecular dynamics simulation on burst and arrest of stacking faults in nanocrystalline Cu under nanoindentation[J]. Nanotechnology, 2003, 14(11): 1208. DOI:10.1088/0957-4484/14/11/009 |
| [13] |
GUO Y, XU T, LI M. Generalized type Ⅲ internal stress from interfaces, triple junctions and other microstructures in nanocrystalline materials[J]. Acta Materialia, 2013, 61(13): 4974-4983. DOI:10.1016/j.actamat.2013.04.048 |
| [14] |
GUO Y, XU T, LI M. Hierarchical dislocation nucleation controlled by internal stress in nanocrystalline copper[J]. Applied Physics Letters, 2013, 102(24): 241910. DOI:10.1063/1.4811791 |
| [15] |
赵鹏越. 铜铅合金和多晶铜力学特性及变形机理的研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. ZHAO Pengyue. Research of mechanics property and deformation mechanism of Cu-Pb alloy and polycrystalline copper based on molecular dynamics simulation[D]. Harbin: Harbin Institute of Technology, 2016. |
 2018, Vol. 50
2018, Vol. 50


