2. 辽宁科技学院 电气与信息工程学院,辽宁 本溪 117004
2. School of Electrical and Information Engineering, Liaoning Institute of Science and Technology, Benxi 117004, Liaoning, China
现代车辆变速器的主要特征是挡位数量多和自动换挡功能.增加挡位数量可提高动力输出灵活性,保证动力连续,提高换挡品质.例如无极变速器(CVT)具有极佳的舒适性,但由于CVT一般采用金属带传动,部分还使用液力变矩器,存在传递扭矩较小,液力效率较低等问题.现有一种新型模块化变速器,其主要特征包括:1)采用大重合度齿形和多锥摩擦片,啮合齿数在6以上,可提高承载力和工作寿命; 2)采用双内啮合共面齿圈,单排只有一个行星轮,减少了零件数量,缩小了变速器体积; 3)每个模块可独立控制实现2挡或4挡变速,n个2挡模块串联可获得2n种挡位,多态挡位下可接近无级变速的效果; 4)变速器可通过外部换挡液压系统控制实现自动换挡.
新型模块化变速器比传统变速器在性能上具有明显优势,为进一步实现其自动换挡和实用化,必须研究其换挡动态特性.
液压式换挡是由液压油带动传动件的脱离结合实现换挡的一种主流方法,液压充油过程会影响变速器的换挡品质.现有针对液压式换挡变速器换挡动态特性的研究主要集中在换挡品质、液压阀特性和控制方法方面. Meng等[1]分析了压力变化趋势对湿式离合器换挡品质的影响;Zhao[2]、Kim[3]、Kulkarni[4]和徐立友等[5]通过离合器动力学建模提出了提高双离合式自动变速器(DCT)换挡品质的压力控制方法;于鸿昶[6]、冯能莲等[7]对液压控制阀进行了仿真建模,马彪[8]、杨树军等[9]建立了包括离合器和充液阀的动力仿真模型,张炳力等[10]从整车角度开展对液压换挡机构的设计分析.由于液压式换挡变速器元件数量多且相互作用复杂,在国内,通过液压缸和传动系整体建模研究换挡动态特性的比较少,暂未发现有针对该新型模块化变速器液压换挡过程的研究.
本文针对一台具有两挡的模块化变速器试验样机进行换挡动态特性分析, 建立了包括传动系、换挡活塞在内的总体动力学模型, 设计了溢流调压换挡液压系统,通过换挡试验验证模型的可信度; 以输出扭矩变化率和输入轴最低转速作为评价指标,通过仿真计算,分析了活塞充油流量和复位弹簧预紧量对换挡品质的影响.
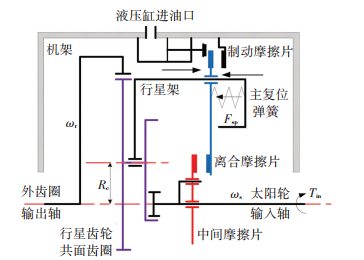
1 新型变速器模块结构两挡变速器模块结构如图 1所示.变速器以外齿圈作为输出轴,行星轮采用双内啮合共面齿圈,输入轴与太阳轮固连,向行星轮传动.湿式离合摩擦片(简称离合摩擦片)与行星架固连且可以轴向运动;中间摩擦片与输入轴通过花键连接.液压缸和主复位弹簧可控制离合摩擦片与中间摩擦片或制动摩擦片贴合,实现行星架随输入轴转动或制动,改变传动比.为保证制动可靠,液压缸与制动摩擦片从两面分别对离合摩擦片制动.
|
图 1 变速器结构 Figure 1 The structure of transmission |
该样机有两挡,当离合摩擦片与中间摩擦片贴合时为一挡,总传动比为1;当离合摩擦片连同行星架被制动时为二挡,样机传动比为2.12.由于升挡过程中液压缸推动离合摩擦片时会对其制动,若离合摩擦片与中间摩擦片未脱离,制动扭矩会向输入轴传递,导致冲击和制动,因此充油流量会通过换挡速度影响换挡过程的品质.主复位弹簧采用波形弹簧,可通过行星架上的螺纹调整预紧,行星架和中间摩擦片之间设置副弹簧辅助两者分离.
2 变速器样机动力学分析与建模目前,对于行星齿轮系的动力学分析主要有弹性体和多刚体两类数学模型.一般基于扭转-振动弹性模型分析行星齿轮系啮合刚度和振动[11];而分析总体输入输出特性可使用凯恩方程等刚体动力学方法[12].为建立传动系简化动力学模型,首先对系统进行以下假设:1)所有零件均为刚体,不考虑转动或平移时弹性模量,约束是理想的;2)忽略齿轮啮合的摩擦力,保留平移、转动时系统的摩擦因数;3)样机采用标准渐开线齿形,节点处的啮合角度不变,啮合情况由力变化反映, 忽略了动载荷.
2.1 转动刚体动力学分析传动系中各零件的运动、惯性参数等如表 1所示,其中惯性参数包括转动半径、转动惯量和质量,约束表示零件通过花键等方式连接,转速相同.行星轮自转与公转分开表示.
| 表 1 传动系统运动与约束关系 Table 1 Movement and constraint of transmission |
结合图 1所示,零件平移运动方向以向制动摩擦片靠近为正,以向左复位为负,转动以与输入扭矩同向为正,可得转动刚体动力学方程为
| $ {J_{\text{r}}}{{\dot \omega }_{\text{r}}} + {f_{\text{r}}}{\omega _{\text{r}}} + {T_{{\text{out}}}} = {F_{\text{r}}}{R_{\text{r}}}\cos {\alpha _{\text{r}}}, $ |
| $ {J_{\text{c}}}{{\dot \omega }_{\text{c}}} + {f_{\text{c}}}{\omega _{\text{c}}} = {T_4} - {F_{{\text{ct}}}}{R_{\text{c}}}, $ |
| $ {J_{{\text{sc}}}}{{\dot \omega }_{{\text{sc}}}} + {f_{{\text{sc1}}}}{\omega _{{\text{sc}}}} = {T_1} - {T_4} - {T_{\text{b}}}, $ |
| $ {J_{{\text{mc}}}}{{\dot \omega }_{{\text{mc}}}} + {J_{{\text{mc1}}}}{\omega _{{\text{mc}}}} = {T_3} - {T_1}, $ |
| $ {J_{\text{s}}}{{\dot \omega }_{\text{s}}} + {f_{\text{s}}}{\omega _{\text{s}}} = {T_{{\text{in}}}} - {T_2} - {T_3}. $ |
式中:T1为离合摩擦片与中间摩擦片传递转矩, T2为行星齿轮与太阳轮传递扭矩, T3为太阳轮花键对中间摩擦片传递扭矩, T4为离合摩擦片对行星架传递扭矩, Tb为离合摩擦片受到总制动摩擦扭矩, Fct为行星架对行星齿轮公转运动切向力, Tin为外部向太阳轮输入扭矩.
2.2 内啮合共面齿圈受力简化模型首先可确定行星齿轮的传动比关系为
| $ \frac{{{\omega _{\text{s}}} - {\omega _{\text{c}}}}}{{{\omega _{\text{p}}} - {\omega _{\text{c}}}}} = \frac{{{N_{{\text{pi}}}}}}{{{N_{\text{s}}}}} = {K_{\text{i}}}, $ |
| $ \frac{{{\omega _{\text{r}}} - {\omega _{\text{c}}}}}{{{\omega _{\text{p}}} - {\omega _{\text{c}}}}} = \frac{{{N_{{\text{po}}}}}}{{{N_{\text{r}}}}} = {K_{\text{o}}}. $ |
式中:ωp为行星轮自转与公转合成角速度, Npi为行星轮内齿面齿数, Npo为行星轮外齿面齿数.
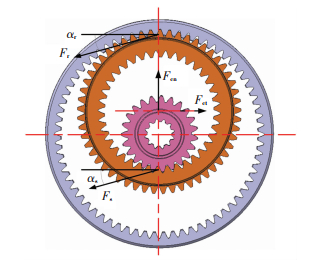
行星轮系受力状态如图 2所示.
|
图 2 行星齿轮受力状态 Figure 2 Stress state of planetary gear |
各齿轮的动力学关系为
| $ {m_{\text{p}}}{{\dot \omega }_{{\text{pre}}}}{R_{\text{c}}} = {F_{{\text{ct}}}} - {F_{\text{r}}}\cos {\alpha _{\text{r}}} - {F_{\text{s}}}\cos {\alpha _{\text{s}}}, $ |
| $ {J_{{\text{pro}}}}{{\dot \omega }_{{\text{pro}}}} + {f_{{\text{pro}}}}{\omega _{{\text{pro}}}} = {F_{\text{s}}}\cos {\alpha _{\text{s}}}{R_{{\text{pi}}}} - {F_{\text{r}}}\cos {\alpha _{\text{r}}}{R_{{\text{po}}}}, $ |
| $ {T_2} = {F_{\text{s}}}{R_{\text{s}}}\cos {\alpha _{\text{s}}}. $ |
式中:ωpre为行星轮公转角速度, ωpro为行星轮自转角速度, Fs为行星轮与太阳轮啮合力, Fr为行星轮与外齿圈啮合力.
行星轮公转时,轴承和行星架向行星轮提供径向离心运动约束力Fcn,该力仅与转速有关,不对其他零件作用,齿轮之间啮合角αs、αr取标准值.
2.3 摩擦片轴向平移离合摩擦片的轴向受力情况为
| $ {m_{{\text{mc}}}}{{\ddot x}_{{\text{mc}}}} + {f_{{\text{mc2}}}}{{\dot x}_{{\text{mc}}}} + {K_{{\text{mc}}}}{x_{{\text{mc}}}} = {F_{{\text{sps}}}} - {{F'}_{{\text{sp}}}}, $ |
| $ {m_{{\text{sc}}}}{{\ddot x}_{{\text{sc}}}} + {f_{{\text{sc2}}}}{{\dot x}_{{\text{sc}}}} + {K_{{\text{sc}}}}{x_{{\text{sc}}}} = {F_{{\text{cy}}}} + {{F'}_{{\text{sp}}}} - {F_{{\text{sp}}}} - {F_{{\text{bc}}}}, $ |
| $ {m_{{\text{cy}}}}{{\ddot x}_{{\text{cy}}}} + {f_{{\text{cy}}}}{{\dot x}_{{\text{cy}}}} + {K_{{\text{cy}}}}{x_{{\text{cy}}}} = {P_{{\text{cy}}}}{S_{{\text{cy}}}} - {F_{{\text{cy}}}}, $ |
| $ {F_{{\text{sps}}}} = {K_{{\text{sps}}}}{x_{{\text{sps}}}}, $ |
| $ {F_{{\text{sp}}}} = {K_{{\text{sp}}}}{x_{{\text{sp}}}}. $ |
式中:Fsp为主复位弹簧对离合摩擦片的推力,Fsps为副弹簧对中间摩擦片的推力,F′sp为中间摩擦片与离合摩擦片之间压紧力,Fbc为制动摩擦片与离合摩擦片之间压紧力,Fcy为液压缸对离合摩擦片的推力,Ccy为活塞初始位置到离合摩擦片的间隙,Csp为主复位弹簧预紧量(初始压缩量),Csps为副弹簧预紧量.
离合摩擦片与中间摩擦片之间的压紧力F′sp是决定两摩擦片传递扭矩的关键参数.由于样机中采用液压活塞抵消弹簧力使得两摩擦片分离,因此取弹簧力与活塞推力的合力表示压紧力F′sp.当活塞位移超过中间摩擦片限位后,两片脱离,压紧力为0,即
| $ {{F'}_{{\rm{sp}}}} = \left\{ \begin{array}{l} {F_{{\rm{sp}}}} - {F_{{\rm{cy}}}} + {F_{{\rm{sps}}}},\\ 0,\;\;\left( {{x_{{\rm{mc}}}} \ge 0.8} \right). \end{array} \right. $ | (1) |
考虑零件结构约束和运动限位,可确定直线运动零件位移关系:
| $ {x_{{\rm{sc}}}} = {x_{{\rm{cy}}}} - {C_{{\rm{cy}}}}, $ |
| $ {x_{{\rm{sps}}}} = {C_{{\rm{sps}}}} - {x_{{\rm{mc}}}}, $ |
| $ {x_{{\rm{sp}}}} = {x_{{\rm{sc}}}} + {C_{{\rm{sp}}}}, $ |
| $ {x_{{\rm{mc}}}} = {x_{{\rm{sc}}}}\left( {{x_{{\rm{mc}}}} \le 0.8} \right). $ |
分开考虑离合摩擦片两面的制动扭矩,根据压紧力计算摩擦片之间传递扭矩如下:
| $ \left\{ \begin{array}{l} {T_{{\rm{b1}}}} = \frac{{2n{\mu _{\rm{f}}}\left( {R_{{\rm{bo}}}^3 - R_{{\rm{bi}}}^3} \right)}}{{3\left( {R_{{\rm{bo}}}^2 - R_{{\rm{bi}}}^2} \right)}}{F_{{\rm{cy}}}},\\ {T_{\rm{b}}} = {T_{{\rm{b1}}}} + {T_{{\rm{b2}}}},\\ {T_{{\rm{b2}}}} = \frac{{2n{\mu _{\rm{f}}}\left( {R_{{\rm{bo}}}^3 - R_{{\rm{bi}}}^3} \right)}}{{3\left( {R_{{\rm{bo}}}^2 - R_{{\rm{bi}}}^2} \right)}}{F_{{\rm{bc}}}}. \end{array} \right. $ | (2) |
式中Tb1为液压缸对离合摩擦片的制动扭矩,Tb2为制动摩擦片对离合摩擦片的制动扭矩.
根据式(1)得离合摩擦片和中间摩擦片压紧力后,可求两摩擦片之间的滑摩扭矩T1为
| $ {T_1} = \frac{{2n{\mu _{\rm{f}}}\left( {R_{{\rm{co}}}^3 - R_{{\rm{ci}}}^3} \right)}}{{3\left( {R_{{\rm{co}}}^2 - R_{{\rm{ci}}}^2} \right)}}{{F'}_{{\rm{sp}}}}. $ | (3) |
摩擦因数受到振动、润滑及转速的影响[13-14],张志刚等[15]通过拟合给出了一种摩擦因数的计算式.考虑到制动摩擦片静止,实测滑摩因数变化范围在0.02以内,为简化运算,仿真滑摩因数取常数.
2.5 活塞流量与运动速度摩擦片移动速度由活塞决定,而活塞的运动速度由输入流量Qcy决定,建立流量平衡方程如下:
| $ {Q_{{\rm{cy}}}} = {S_{{\rm{cy}}}}{{\dot x}_{{\rm{cy}}}} + \Delta Q + {Q_{\rm{p}}}. $ |
式中:ΔQ为液压缸泄漏量, Qp为活塞内部压力变化时由油液压缩性造成的流量损失,即
| $ {Q_{\rm{p}}} = \frac{V}{K}\frac{{{\rm{d}}{P_{{\rm{cy}}}}}}{{{\rm{d}}t}} = \frac{{{S_{{\rm{cy}}}}{x_{{\rm{cy}}}} + {V_0}}}{K}\frac{{{\rm{d}}{P_{{\rm{cy}}}}}}{{{\rm{d}}t}}. $ |
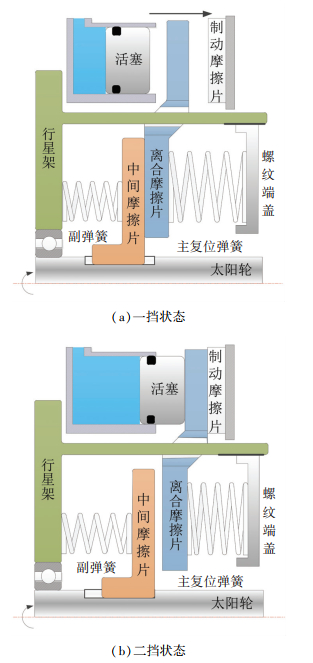
离合摩擦片是换挡关键元件,要确定其扭矩状态,必须确定摩擦片相互压紧力.一挡时活塞不接触离合摩擦片,直到油压上升活塞接触并推动离合摩擦片运动到制动摩擦片位置,如图 3所示.根据活塞位置,可将升挡过程分为4个阶段分析离合摩擦片受力.
|
图 3 一、二挡换挡元件位置 Figure 3 Position of shift components in gear one and two |
1) 活塞快速消除间隙,直至接触离合摩擦片.此时Fbc=0,F′sp=Fsp,Fcy≈0.
2) 液压缸推力Fcy随压力上升克服主弹簧力,中间摩擦片与离合摩擦片之间压力F′sp逐渐减小,如图 4所示.根据式(2)~(3)可知,最大扭矩与压力成正比,因此在压力出现重合的t1~t2时间段内,离合摩擦片的制动扭矩Tb和驱动扭矩T1也必然出现重合,此时扭矩T1对输入轴的作用是制动,因此变速器换挡出现制动和冲击.缸容积不变时,压力上升速度由充油流量决定,从而影响重合区域面积,因此制动时间和冲击大小与流量有关,扭矩初值则与弹簧预紧力有关.

|
图 4 离合摩擦片受力变化 Figure 4 Stress and torque state of friction disk |
3) Fcy克服主弹簧力Fsp继续移动,但未接触制动摩擦片.中间摩擦片与离合摩擦片分离F′sp为0.离合摩擦片受到持续制动可能静止.此时Fbc=0,F′sp=0,Fcy≥Fsp.
4) 离合摩擦片走完行程,受到活塞和制动器摩擦片双面制动完全静止,缸内压力最终等于油源压力.此时Fbc=PsScy-Fsp=Fcy-Fsp,F′sp=0,其中Ps为油源压力,Scy为活塞面积.
2.7 仿真模型建立根据上述分析,用MATLAB/Simulink建立仿真模型,部分参数见表 2.
| 表 2 部分模型参数 Table 2 Parameters of model |
变速器模型如图 5所示,仿真可调整变速器输入输出参数、充油流量和弹簧预紧量,运动限位利用条件模块简化表示.

|
图 5 变速器仿真模型 Figure 5 Simulation model of transmission |
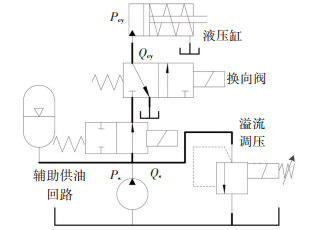
为实现样机的液压换挡,设计了一种溢流阀调压的简化换挡液压系统(图 6),该换挡系统主要包括蓄能器、溢流阀、充液控制阀和直通换向阀.在油源压力不足时,充液控制阀能切断液路,并由泵进行充液升压,由蓄能器进行保压并补充流量.系统通过溢流阀控制油源压力保持稳定,换挡时由直通换向阀控制系统向液压缸输出一定流量的液压油.液压缸内部压力升高与流量大小有关,根据油液压缩性关系可以计算液压缸内压力上升速度:
| $ \frac{{\Delta {P_{{\rm{cy}}}}}}{{\Delta t}} = {\mu _{\rm{p}}}K\frac{{{Q_{{\rm{cy}}}}}}{V}. $ |
|
图 6 换挡液压系统 Figure 6 Hydraulic shift system |
式中:K为液压油弹性模量, Qcy为液压系统向液压缸输入流量, V为充油时液压缸密闭腔容积, μp为修正系数.
实验选定油源压力Ps上限为3.1 MPa.受到输油管线通径、距离和低压溢流影响,此时系统向活塞提供的流量Qcy保持在5 mL·s-1左右,考虑样机液压缸容积,实验中换挡速度和压力升高速度较低,因此不需要增加缓冲阀组.
3.2 传感器及样机驱动变速器模块采用液压马达驱动(图 7),油泵电机最大功率为30 kW.马达可向变速器输入轴提供转速200 r·min-1以下的恒转速输入,输出端保持5.5 N·m的恒扭矩负载.系统的扭矩和转速数据通过转速扭矩传感器和PLC记录,记录频率1 Hz.为了读取液压活塞的内部压力变化,在样机外部插装压力传感器,再通过模拟量采集卡进行压力记录,采集周期取1 s.

|
图 7 模块化变速器样机 Figure 7 Modular transmission |
开机后调节液压马达输出转速至191 r·min-1,启动换挡液压系统,待油源压力稳定在3.1 MPa后,换向阀通电换挡.记录输入轴扭矩、输出转速和液压缸内部压力变化.仿真模型的工况设置与实验一致,结果如图 8所示.
|
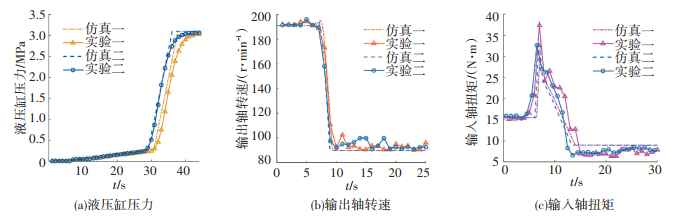
图 8 液压缸压力及轴转速扭矩变化 Figure 8 Pressure of cylinder and speed/torque of shafts |
第一和第二次实验分别采用流量为4.5、4.7 mL·s-1.随着液压缸压力增大,油缸进油口压差减小,实际充油流量逐渐减小,压力上升速度减慢,因此最终阶段仿真压力上升比实际稍快.由图 8(a)可知,换挡过程的压力上升分为3个阶段:1)活塞消除间隙,油压上升至0.05 MPa附近,达到弹簧预紧力.实验时分别用时2 s和1 s,仿真用时1.47 s和1.37 s. 2)活塞克服弹簧作用,压力缓慢增加,直到离合摩擦片接触制动摩擦片.实验时分别用时22 s和21 s,仿真用时22.3 s和21.4 s. 3)活塞静止后,压力快速上升至系统压力3.1 MPa.输入流量越大,液压缸压力升高越快,充油过程时间越短.
3.4 扭矩转速变化分析由于换挡后液压马达负载减小,机械效率上升,马达供油回路工作压力减小,导致最终转速与仿真存在误差.并且仿真忽略了行星轮系的动载荷,因此实际转矩存在一定幅度波动.由图 8(b)可知,换挡完成后,仿真输出转速为89 r·min-1,实验转速在90~99 r·min-1,误差<9%.
对于输入轴扭矩,由于离合摩擦片与活塞接触制动,扭矩出现明显冲击,之后输入轴扭矩逐渐下降直到两摩擦片完全分离.根据图 8(c)可知,两次仿真扭矩峰值分别为33.81和33.57 N·m,之后随离合摩擦片所受压力下降而减小.实验测得峰值为37.36和32.56 N·m,误差9.5%以内;在换挡完成后,仿真扭矩为8.95 N·m,实际扭矩平均值为8.34和8.57 N·m,误差为7%.
3.5 换挡时间分析受到实际充油流量减小和不同设备记录时间误差的影响,换挡实验过程相比仿真略慢.如图 8(a)所示,样机实际换挡时间约4 s,仿真换挡用时分别为2.85 s和2.77 s.换挡时间远小于液压缸走完行程的时间,因为换挡完成以离合摩擦片完全制动为标志,当液压缸推力足够大时,离合摩擦片在接触制动摩擦片之前停转.因此换挡过程在压力变化第2)阶段开始后很快结束.
液压缸推力由负载决定,主弹簧作为负载,负载力与液压缸位移正相关,而液压缸的运动速度由流量决定.因此流量越大,液压缸推力上升越快,换挡时间越短.
对比仿真与实验,相同工况下模型仿真结果与实际样机换挡过程较好对应,模型可以作为研究变速器换挡过程的参考.
4 流量及预紧量对换挡特性影响充油流量和弹簧预紧量决定了摩擦片传递扭矩T1的初值和变化率,最终影响制动和冲击.通过仿真实验确定流量和预紧量对换挡特性的影响.
目前,对于变速器换挡特性的主要评价指标是冲击度和速度波动,冲击度是车辆加速度的变化率,与变速器输出扭矩变化率有关,即
| $ J = \frac{{{\rm{d}}a}}{{{\rm{d}}t}} = \frac{{{r_{\rm{w}}}}}{{{i_0}{I_{\rm{w}}}}}\frac{{{\rm{d}}{T_{{\rm{out}}}}}}{{{\rm{d}}t}}. $ |
式中:i0为驱动桥传动比,rw为车轮动力半径, Iw为与输出轴相连转动体惯量,Tout为变速器输出扭矩.
由于样机暂无对应的车型,因此将最小输出扭矩变化率作为样机换挡冲击的评价标准.由于换挡过程制动现象导致输入轴转速下降,这会影响发动机正常工作,因此以输入轴最低转速作为换挡制动评价标准.
由于换挡过程较快,车速或变速器输出转速基本不变,发动机在油门开度和转速不变时输出扭矩基本不变.根据样机的传递扭矩设计指标,仿真取60 N·m恒扭矩输入,输出转速恒定为400 r·min-1,为提高换挡速度,仿真取流量为27~33 L·min-1,弹簧预紧量在5~15 mm,可通过模型调整.
4.1 最低输入转速及换挡时间影响分析由图 9可得,在相同预紧15 mm情况下,换挡时间随流量增大而减少.流量为33 L·min-1时,最短换挡时间0.43 s,各工况下最低转速如表 3所示.

|
图 9 预紧15 mm输入轴转速 Figure 9 Speed of input shaft (preload 15 mm) |
| 表 3 各工况最低输入轴转速 Table 3 Minimum speed of input shaft |
流量27 L·min-1以上时,输入轴未见降速,对比5~15 mL·s-1小流量换挡,大流量快速换挡有效消除了制动现象.流量5 mL·s-1且预紧量较大时会出现负转速,对应实际情况表明车辆制动,应禁止换挡.根据过程分析,流量相同时预紧量越大会导致扭矩T1初始值增大,制动增加.因此增大流量,减小预紧量可提高换挡速度,减少动力损失.
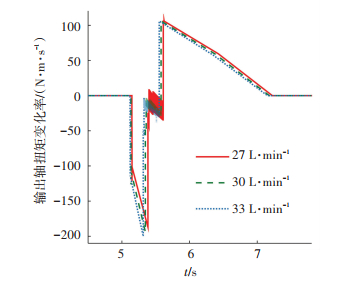
4.2 扭矩变化率的影响分析15 mm预紧时输出扭矩变化率如图 10所示,换挡出现明显负向冲击.换挡完成之后,由于仿真输入扭矩不变,输出扭矩在降速增扭作用下相对平缓地正向增加.
|
图 10 预紧15 mm输出扭矩变化率 Figure 10 Output torque change rate(preload 15 mm) |
取各工况下出现的扭矩变化率最小值作为评价负向冲击大小的标准,如表 4所示.
| 表 4 输出最小扭矩变化率 Table 4 Minimum change rate of output torque |
根据输出最小扭矩变化率及输入轴转速可知:
1) 弹簧预紧量不变时,充油流量越大,换挡时间越短,对应扭矩变化率的绝对值越大,即负向冲击越大.
2) 充油流量不变时,弹簧预紧量越大,初始制动扭矩不变,负向冲击越大.增加弹簧预紧量可以提高一挡传递扭矩上限,但会增加换挡制动扭矩初始值,导致换挡冲击和制动增大.
综合比较充油流量及弹簧预紧量对制动扭矩变化率的影响可知,弹簧预紧量对负向冲击的影响明显.实际换挡液压系统的设计与研究时,需要综合考虑预紧量和充油流量对换挡品质和速度的影响.在强调换挡速度时,对流量的调整不应使冲击增加太大;在强调换挡品质时,对预紧量和流量的调整不应使换挡时间过长.
5 结论本文针对一种新型模块化变速器样机的换挡过程进行动力学分析,建立了包括传动系、液压活塞的整体仿真模型,设计了一种溢流液压换挡装置,进行了样机换挡试验.在验证模型可信度基础上,针对活塞充油流量和复位弹簧预紧量,以输出扭矩变化率等为指标,仿真得出了流量和预紧量对样机换挡品质的影响规律:
1) 变速器模块的离合摩擦片在换挡过程受到扭矩重合影响,引起冲击和制动.
2) 复位弹簧的预紧量决定了换挡过程摩擦片所受扭矩初值,预紧量越大导致冲击和制动增加.预紧量应以变速器传递扭矩指标对应预紧量为最大值设置,减少冲击.
3) 活塞的充油流量通过活塞压力变化影响换挡过程,增大流量可有效减少换挡时间和制动,但冲击增加,后续可考虑改造活塞并设计流量控制方法以减少高速换挡的冲击. 5 mL·s-1小流量时,不允许大预紧量换挡.
研究为进一步实现变速器样机的自动换挡功能以及结构优化提供了理论参考.
| [1] |
MENG F, CHEN H Y, ZHANG T, et al. Clutch fill control of an automatic transmission for heavy-duty vehicle applications[J]. Mechanical Systems and Signal Processing, 2015, 64/65: 16-28. DOI:10.1016/j.ymssp.2015.02.026 |
| [2] |
ZHAO Z G, HE L, YANG Y Y, et al. Estimation of torque transmitted by clutch during shifting process for dry dual clutch transmission[J]. Mechanical Systems and Signal Processing, 2016, 75: 413-433. DOI:10.1016/j.ymssp.2015.12.027 |
| [3] |
KIM S, OH J, CHOI S. Gear shift control of a dual-clutch transmission using optimal control allocation[J]. Mechanism and Machine Theory, 2017, 113: 109-125. DOI:10.1016/j.mechmachtheory.2017.02.013 |
| [4] |
KULKARNI M, SHIM T, ZHANG Y. Shift dynamics and control of dual-clutch transmissions[J]. Mechanism and Machine Theory, 2007, 42(2): 168-182. DOI:10.1016/j.mechmachtheory.2006.03.002 |
| [5] |
徐立友, 刘海亮, 周志立, 等. 拖拉机双离合器自动变速器换挡品质评价指标[J]. 农业工程学报, 2015, 31(8): 48-53. XU Liyou, LIU Hailiang, ZHOU Zhili, et al. Evaluation indexes of shifting quality for dual clutch transmission for tractor[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(8): 48-53. DOI:10.3969/j.issn.1002-6819.2015.08.008 |
| [6] |
于鸿昶, 刘奇芳, 陈虹. DCT离合器电液控制阀的非线性压力控制[J]. 吉林大学学报(信息科学版), 2014, 32(5): 484-492. YU Hongchang, LIU Qifang, CHEN Hong. Nonlinear pressure control for clutch electro-hydraulic control valve of DCT[J]. Journal of Jilin University, 2014, 32(5): 484-492. DOI:10.3969/j.issn.1671-5896.2014.05.006 |
| [7] |
冯能莲, 郑慕侨, 马彪. 动力换档离合器充/放油特性仿真研究[J]. 农业工程学报, 2001, 17(2): 68-71. FENG Nenglian, ZHENG Muqiao, MA Biao. Performance simulation of power shift clutch during charge /discharge processes[J]. Transactions of the Chinese Society of Agricultural Machinery, 2001, 17(2): 68-71. DOI:10.3321/j.issn:1002-6819.2001.02.017 |
| [8] |
马彪, 刘影, 陈建文. 车辆综合传动换档离合器结合过程动态特性研究[J]. 中国机械工程, 2000, 11(6): 691-694. MA Biao, LIU Ying, CHEN Jianwen. Study on dynamic performance in engagement process of power shift-steering transmission shift clutch[J]. China Mechanical Engineering, 2000, 11(6): 691-694. DOI:10.3321/j.issn:1004-132X.2000.06.027 |
| [9] |
杨树军, 苑士华, 胡纪滨. 湿式离合器换挡过程动态特性[J]. 农业机械学报, 2005, 36(11): 38-41. YANG Shujun, YUAN Shihua, HU Jibing. Study on dynamic performance in engagement process of wet clutch[J]. Transactions of the Chinese Society of Agricultural Machinery, 2005, 36(11): 38-41. DOI:10.3969/j.issn.1000-1298.2005.11.010 |
| [10] |
张炳力, 季明微, 张友皇. 自动变速器车辆换挡品质研究[J]. 中国公路学报, 2012, 25(3): 141-146. ZHANG Bingli, JI Mingwei, ZHANG Youhuang. Research on the shift quality of qutomatic transmission vehicles[J]. China Journal of Highway and Transport, 2012, 25(3): 141-146. |
| [11] |
巫世晶, 任辉, 朱恩涌, 等. 行星齿轮传动系统动力学研究进展[J]. 武汉大学学报(工学版), 2010, 43(3): 398-403. WU Shijing, REN Hui, ZHU Enyong, et al. Research advances for dynamics of planetary gear trains[J]. Engineering Journal of Wuhan University, 2010, 43(3): 398-403. |
| [12] |
张勇, 许纯新, 宋健, 等. 行星齿轮变速箱换挡过程的建模与仿真[J]. 吉林工业大学学报(工学版), 2002, 32(1): 23-27. ZHANG Yong, XU Chunxin, SONG Jian, et al. Modeling and simulation of shifting process of the planetary gearbox[J]. Journal of Jilin University, 2002, 32(1): 23-27. DOI:10.3969/j.issn.1671-5497.2002.01.005 |
| [13] |
IQBAL S, AL-BENDER F, OMPUSUNGGU A P, et al. Modeling and analysis of wet friction clutch engagement dynamics[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 420-436. DOI:10.1016/j.ymssp.2014.12.024 |
| [14] |
杨世文, 郑慕侨. 摩擦力非线性建模与仿真[J]. 系统仿真学报, 2002, 14(10): 1365-1368. YANG Shiwen, ZHENG Muqiao. Simulation of nonlinear friction with modeling methodology[J]. Journal of System Simulation, 2002, 14(10): 1365-1368. DOI:10.3969/j.issn.1004-731X.2002.10.027 |
| [15] |
张志刚, 周晓军, 沈路, 等. 湿式离合器动态接合特性的仿真与试验[J]. 中国公路学报, 2010, 23(3): 115-120. ZHANG Zhigang, ZHOU Xiaojun, SHEN Lu, et al. Simulation and experiment on dynamic engagement characteristics of wet clutch[J]. China Journal of Highway and Transport, 2010, 23(3): 115-120. |
 2018, Vol. 50
2018, Vol. 50


