在我国城市道路,机动车道与非机动车道往往是通过机非分隔线来进行车道划分.据分析[1]表明,电动车较自行车更易违规越过白色标线行驶在机动车道,这将形成机动车-电动车的异质交通流.异质交通流内部会形成大量的冲突,从而降低机动车的平均速度.因此,了解影响电动车侵入机动车道的原因以及越界后对机动车流量及通行速度的影响显得尤为重要,将为交叉口的信号控制及机动车、非机动车道的规划、设计和管理提供相应的理论支持.
目前,基于元胞自动机来研究机非混合的交通流微观模型较为广泛[2-5],而充分考虑机动车与电动自行车流特性的微观模型十分有限.现有的机非混合元胞自动机模型第一类是以NaSch模型对机动车流进行模拟[6],将道路空间进行虚拟子空间划分,通过调整机动车的多车道元胞自动机模型的参数来模拟自行车流,但并未考虑到机非混合车道划分概念及跟车行为不典型等特点.第二类以多值元胞自动机来描述自行车流的机非混合交通流,并且模糊了自行车换道规则[7-8],这类模型不适用于研究电动自行车侵入机动车道的行为.虽然基于元胞自动机的机非混合交通流模型具有规则简单、仿真容易实现等特点,但需要分别设置机动车、自行车或电动车模块换道规则和更新规则.
电动自行车的启动加速度比自行车大、平均速度更快,导致其运动摇摆性、成群性、超越性等特点比自行车更加明显.而且电动自行车比自行车体积大,在异质交通流中占用的道路空间更多,对异质交通流造成相对更大的影响.在信号交叉口,绿灯开始时刻,相对自行车,电动自行车可以在很短的时间内进行加速,迅速占领非机动车道甚至是机动车道,对机动车的行驶造成很大干扰.但现有研究基本是针对机动车-自行车异质交通流,比较缺乏机动车-电动车的异质交通流研究.本文在搭建仿真平台时,充分考虑了电动车尺寸、最大加速度及最大速度等特征,使其更接近于真实场景.本文建立的机动车-电动车异质交通流模型是基于社会力模型的,社会力模型是由Helbing[9]首次提出的,但现有的基于社会力的交通流模型主要用于研究机动车与行人的混合交通流[10-11],很少用于机动车-电动车的研究.所以本文在原始社会力模型的基础上,为了能够描述出电动车侵入机动车道的状态,引入了间隙力、跟驰力和排斥力,使其更还原真实场景.对新建模型进行标定与验证后,分析了电动车排队数量和到达率对机动车流量及平均通行速度的影响.
1 模型建立在信号交叉口内,可能由于电动自行车的干扰,使机动车的通行区域受到限制,导致驾驶员的行为与无干扰情况有较大区别.通过仔细观察存在电动自行车干扰下的信号交叉口驾驶员的实际行为,驾驶员行为可分为3种类型:自由驾驶行为、跟驰行为和穿梭行为.自由驾驶行为是指机动车或电动自行车可以自由通过交叉口而不受其他车辆阻碍的驾驶行为.这种行为主要属于处于停车线最前列的机动车和电动自行车.当绿灯开始时,最前列车辆,首先离开停车线,逐渐加速,直至到达交叉口的限速.因此,它们的速度仅受交叉口限速的限制. 图 1说明在有电动车干扰下的驾驶员行为,其中蓝色机动车(1, 2)和电动自行车采用自由驾驶行为.

|
图 1 电动自行车干扰下的交叉口驾驶行为 Figure 1 Driving behavior at an intersection with interference of electric bicycles |
跟驰行为是指当机动车和电动自行车通过信号交叉口时,跟随前车行驶,这与微观交通流中跟驰行为的含义相同.这种行为发生在机动车或电动自行车不能超越其他车辆以获得前方位置或无法找到超车空间以获得速度优势时.在图 1中,黑色机动车(4, 8, 10, 11, 12, 13, 14, 15)和电动自行车采用跟驰行为.
在穿梭行为中,车辆不断寻找可通行的空隙,以获得更快的速度或更前方的位置.出现这种行为的车辆往往是速度更快的车辆,类似于速度更快的鱼穿过一群慢鱼的情形.由于电动自行车体积小,加速度大,灵活性高,所以相对于机动车这种穿梭行为更加明显.在穿梭行为中,穿梭车首先要寻找一个可通行的间隙,然后在不发生与其他车辆碰撞的前提下通过间隙.在图 1中,红色机动车(3, 5, 6, 7, 9)和电动自行车采用穿梭行为.
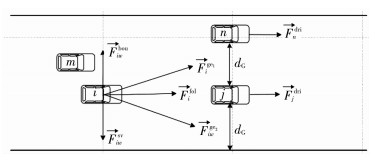
根据上述驾驶员行为分析,发现现有的社会力模型不能直接应用于信号交叉口机动车-电动车异质交通流建模.因此,本文提出了一种新的模型,可以捕捉电动车占用机动车行驶空间而对机动车造成干扰的交通流特性.对应于上述驾驶员行为,存在5种社会力:前向自驱动力、跟驰力、间隙力、车辆排斥力和边界排斥力. 图 2显示了车辆在交通流中可能产生的力.
|
图 2 城市信号交叉口社会力模型受力 Figure 2 Social force model of urban signalized intersection |
1) 前向自驱动力.这里的自驱动力加入加速度限制以确保机动车和电动自行车的加速度不超过其最大加速度,该力可使车辆在每个适应时间内调整其速度,以达到交叉口所允许的最大速度.前向自驱动力的计算公式为
| $ \vec F_j^{{\rm{dri}}} = \min \left\{ {{a_{\max }},v_j^0\left( t \right)e_j^0 - {v_j}\left( t \right)/{\tau _j}} \right\}. $ | (1) |
式中:amax为车辆通过信号交叉口的最大加速度;vj0(t)、vj(t)分别为车辆j的期望速度和实际速度;ej0为车辆j的期望运动方向;τj为车辆j的适应时间.
2) 跟驰力.跟驰力属于跟驰行为, 首先在机动车和电动自行车行驶中,如果与其他车辆接触,就会发生撞车事故,因此本文在下面的车辆上加上防撞算法,以确保安全.其次,本文的跟驰力可以是负的.跟驰力的正负,取决于跟驰车辆的速度和预定义的安全速度之间的关系.如果后车速度小于安全速度跟驰力便是正的,使车辆加速;如果后车的速度超过安全速度跟驰力便是负的,使车辆减速;如果后车的速度等于安全速度,跟驰力为零,车辆保持原有速度.与自驱动力一样,本文也给出了加速度的最大值限制,表达式为
| $ \vec F_i^{{\rm{fol}}} = \min \left\{ {{a_{\max }},v_i^{{\rm{safe}}}\left( {{g_i},{v_i},{v_j}} \right) - {v_i}\left( t \right)/{\tau _i}} \right\} \cdot {{\vec n}_{i,j}}. $ | (2) |
式中:amax为保证车辆安全通过信号交叉口的最大加速度;gi为行驶过程中前后车的安全距离;
| $ \begin{array}{*{20}{c}} {v_i^{{\rm{safe}}}\left( {{g_i},{v_i},{v_j}} \right) = - {b_i}{\tau _i} + }\\ {\sqrt {b_i^2\tau _i^2 + {b_i}\left\{ {2{g_i}\left( t \right) - {\tau _i}{v_i}\left( t \right) + \frac{{v_j^2\left( t \right)}}{{{b_j}}}} \right\}} .} \end{array} $ | (3) |
式中bi、bj为车辆i与其前车j的最大减速度,gi(t)指跟驰车辆与前车的距离.
3) 间隙力.用间隙力来表示穿梭行为,当机动车或电动自行车间隙宽度dG大于车身长度df与车辆安全侧边距Δd(如后视镜宽度)之和时,间隙力的大小随着间隙的增大而增大,否则间隙力为0,表达式为
| $ \begin{array}{l} \vec F_i^{{\rm{ge}}} = \\ \left\{ \begin{array}{l} {A^{\rm{G}}}\exp \left[ {\frac{{{d_{\rm{G}}} - \left( {{d_{\rm{f}}} + 2\Delta d} \right)}}{{{d_{\rm{f}}} + 2\Delta d}}} \right] \cdot {{\vec n}_{i,j}},{d_{\rm{G}}} > {d_{\rm{f}}} + 2\Delta d;\\ 0,{d_{\rm{G}}} \le {d_{\rm{f}}} + 2\Delta d. \end{array} \right. \end{array} $ | (4) |
式中:AG为可插间隙吸引力的作用强度;df为车辆的车身宽度;Δd为车辆一侧的安全侧边距;dG代表前方两车之间形成的可插间隙宽度,左右两车形成的可插间隙宽度越大则间隙力越大;
4) 排斥力.为了避免机动车和电动自行车与左右相邻车辆发生碰撞或者避免越过边界线,目标车辆需与其他车辆或者边界保持一个距离,将这样的力称为排斥力[9-10].与初始社会力模型中的排斥力形式相似,用一个指数函数来表示,两车之间或车与边界的距离若在作用范围内,则两车或车与边界之间排斥力随距离的增大而减小,反之排斥力为0.车辆间排斥力的表达式为
| $ \begin{array}{l} \vec F_{im}^{{\rm{sv}}} = \\ \left\{ \begin{array}{l} {A^{\rm{P}}}\exp \left[ {\left( {{d_{im}} - {B_1}} \right)/{B_1}} \right] \cdot {{\vec n}_{mi}},{d_{im}} < {B_1};\\ 0,{d_{im}} \ge {B_1}. \end{array} \right. \end{array} $ | (5) |
式中:A1P为车辆i与车辆m之间排斥力的作用强度;B1为作用范围,取为0.8 m[13];dim代表车辆之间的实际距离,两车距离越近则排斥力越大;
车辆在驶入道路的边界区域时,因受到道路边界w的影响,车辆会与边界之间产生排斥力.车与行驶边界之间的排斥力记为
| $ \begin{array}{l} \vec F_{iw}^{{\rm{bou}}} = \\ \left\{ \begin{array}{l} A_2^{\rm{P}} \cdot \exp \left[ {\left( {{d_{iw}} - {B_2}} \right)/{B_2}} \right] \cdot {{\vec n}_{wi}},{d_{iw}} < {B_2};\\ 0,{d_{iw}} \ge {B_2}. \end{array} \right. \end{array} $ | (6) |
式中:A2P代表车辆与边界之间排斥力的作用强度;B2为车辆与边界之间的作用范围,取0.8 m[13];diw分别代表车辆与车道边界的实际距离,距离越近则排斥力越大;
综上所述,若车辆为头车时,主要受驱动力向前行驶,同时也会受到来自边侧车和边界的排斥力,头车所受合力为
| $ {{\vec F}_{{\rm{lead}}}} = \vec F_j^{{\rm{dri}}} + \vec F_{jm}^{{\rm{sv}}} + \vec F_{jw}^{{\rm{bou}}}. $ | (7) |
若车辆为跟驰车辆时,受到前车的跟驰力,在存在可插间隙时还受到前方的间隙力,二者取其较大值;同时也会受到来自边侧车和边界的排斥力,跟驰车辆所受合力为
| $ {{\vec F}_{{\rm{fol}}}} = \max \left( {\vec F_i^{{\rm{fol}}},\vec F_i^{{\rm{ge}}}} \right) + \vec F_{im}^{{\rm{sv}}} + \vec F_{iw}^{{\rm{bou}}}. $ | (8) |
本文主要是分析信号交叉口电动自行车数量较多时对机动车的影响,最终选定成都市二环蜀汉路口为数据采集地点.此交叉口的二环路西二段方向和蜀汉路方向的机动车流量都较大,在绿灯开始之前有较大数量的电动车聚集在离机动车停车线大概9 m的位置处.在右转车辆数较少的情况下,本文只分析电动车辆对直行机动车流量的影响.此外,二环蜀汉路口的电动车数量较大时,明显可以观测到已经占用了机动车的行驶道路资源,如图 2所示,这正是本文需要研究的内容.
为了掌握信号交叉口流量的一般趋势及车辆通行的特点,最终采集时间为非节假日且天气状况良好的条件下,在晚高峰时期17:30—18:30时段进行交通量调查,该交叉口二环路西二段方向和蜀汉路方向的进、出口车道数均为4条,进口道宽度均为3.25 m,出口道宽度均为3.5 m,非机动车道宽度均为4 m,两个方向都不是机非分离,二环路西二段方向和蜀汉路方向的电动车停车线距机动车停车线距离分别为9 m和6 m.该部分内容统计了两个方向的4个周期的数据,最终取平均值.相关记录调查数据见表 1、2.
| 表 1 二环路西二段方向单周期交通流信息 Table 1 Single cycle traffic flow information on the West Second Section of Second Ring Road |
| 表 2 蜀汉路方向单周期交通流信息 Table 2 Single cycle traffic flow information on the Shuhan Road |
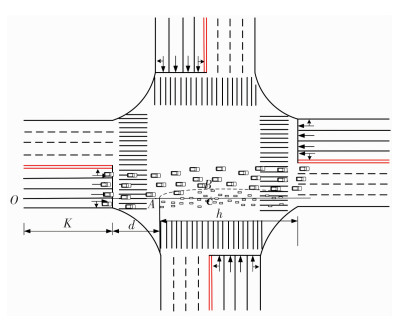
此外,在实地观察时,侵入机动车行驶空间上边界与电动车的排队数量有很大的关系,所以需要对电动车排队数量与上边界的关系进行分析.电动车启动后,由于速度快速增大,电动车之间的间距也随之增大,占据的空间在短时间内迅速扩张,从而会侵入到机动车的行驶空间.电动车侵入机动车行驶空间时并不是简单的直线范围,刚刚开始电动车会在停车线内等待通行,但是行驶到中途时由于电动车速度快,灵活高,会在大约h/2位置处达到一个最大侵入位置,所以在仿真平台搭建时使用抛物线.如图 3所示,在仿真程序设置电动自行车可达上边界时,取点A与点B之间所连接的抛物线(B点为抛物线顶点,A点为抛物线上一点,采用顶点式确定抛物线表达式)加上从B点开始延伸至出口道的直线,令A(xa, ya),B(xb, yb).
|
图 3 电动车侵入机动车道 Figure 3 Diagram of electric bicycles invading the motor lanes |
本次调查的相关参数分别如下:d=7 m,h=30 m.在搭建仿真平台时将O点作为原点,即O(0, 0),所以A(xa, ya)=A(d, 0).电动车的行驶轨迹最高点B的横坐标xb大概是h/2,纵坐标与电动车的排队数量有很大关系,呈线性增加的趋势.根据交通实地调查的规律与相关的数据可知,当排队数量为20辆时,大概会占用3.25 m,取yb=3.25/20·N,那么B(xb, yb)=B(h/2, 3.25/20·N),其中N为电动自行车的排队数量.在仿真过程中,随着N的改变,电动自行车可行驶的上边界也随之改变,从而影响着机动车辆的通行.
若令纵坐标为
| $ y = a{\left( {x - {x_b}} \right)^2} + b, $ | (9) |
其中
| $ \left\{ \begin{array}{l} a = \frac{{{y_b} - b}}{{{{\left( {{x_b} - {x_a}} \right)}^2}}},\\ b = {x_b}, \end{array} \right. $ | (10) |
则
| $ y = \frac{{\frac{{3.25N}}{{20}} - b}}{{{{\left( {\frac{h}{2} - d} \right)}^2}}}{\left( {x - \frac{h}{2}} \right)^2} + \frac{h}{2}. $ | (11) |
本文调查了一个城市信号交叉口的两个不同方向的数据,其中二环路西二段方向数据将被用作进行模型的参数标定,二环路西二段方向数据将被用来进行模型的验证.本文所提出的异质交通流社会力模型参数的标定是求解一个非线性规划问题,目标函数为由待标定模型仿真出来的数据与实测数据的误差统计值,约束条件为各个参数的取值范围,表达式为
| $ \begin{array}{*{20}{c}} {\min \omega = \sum\limits_{n = 1}^N {\frac{{\left| {{z_n} - {{\hat z}_n}} \right|}}{{{z_n}}}} .}\\ {{\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {g_i}\left( p \right) = 0,i = 1,2, \cdots ,{N_g};\\ {h_j}\left( p \right) \ge 0,j = 1,2, \cdots ,{N_h}. \end{array} \right.} \end{array} $ | (12) |
式中:ω为目标函数;zn为变量n的实测数据,包括一个周期的有效绿灯时间通过交叉口的机动车辆总数Na、小汽车数Nc、所有车辆的平均时间T、所有车辆的平均速度V;
| 表 3 社会力模型标定参数的取值范围与标定值 Table 3 Parameter and calibration value of social force model |
本论文采用遗传算法进行该非线性规划问题的求解[18],群体多样性过早减少容易导致遗传算法产生局部收敛,这极大地限制了遗传算法的搜索空间,而群体多样性减少主要是由选择、交叉和变异操作所引起的.本文在使用遗传算法进行标定时引入了一些防止算法局部收敛的策略,即保持各代群体都具有一定多样性,采用与个体适应值和群体平均值相关联的自适应交叉率和变异率,最后根据停止准则结束迭代过程.每次迭代都利用建立的仿真平台获得目标函数中4个变量的仿真值,然后求出真实值与仿真值间的误差即目标函数ω值.标定获得的最优参数取值见表 3.
2.2 模型验证通过查阅文献,之前交通流模型验证中[19-20]通常使用的评价指标为平均绝对误差eMAE、平均绝对相对误差eMARE与Theil不等系数(Theil’s inequality coefficient)[21](本文用U表示),其中Theil不等系数常常被用来评价预测效率的优劣,由于精度较高被广泛应用于各个领域模型的验证,本文便将其作为评价指标对新建模型予以评价.各指标表达式分别为
| $ {e_{{\rm{MAE}}}} = \frac{1}{N}\sum\limits_{k = 1}^N {\left| {{z_{r,k}} - {z_{s,k}}} \right|} , $ | (13) |
| $ {e_{{\rm{MARE}}}} = \frac{1}{N}\sum\limits_{k = 1}^N {\left( {\frac{{\left| {{z_{r,k}} - {z_{s,k}}} \right|}}{{{z_{r,k}}}}} \right)} , $ | (14) |
| $ U = \frac{{\sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{\left( {{z_{r,k}} - {z_{s,k}}} \right)}^2}} } }}{{\sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{\left( {{z_{r,k}}} \right)}^2}} } + \sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {{{\left( {{z_{s,k}}} \right)}^2}} } }}. $ | (15) |
式中:Zr, k,Zs, k分别为第k次仿真对应的交通量、平均通行时间或平均通行速度的实际数据与仿真数据;N为仿真次数,这里取10次.
通过实测数据与仿真结果的对比完成了两组数据的误差分析,由于误差值是10次仿真结果的平均值,所以对机动车总数以及小汽车数的绝对误差值进行了取整,最终结果整理见表 4.
| 表 4 模型验证结果 Table 4 Validation results of the model |
从以上表中可以看出本文提出的基于社会力的城市信号交叉口异质交通流模型在对真实交通流进行仿真时的eMARE值均小于12%,说明仿真结果与真实城市信号交叉口的交通状况非常接近,模型可以比较好地反映受电动车干扰较大的机动车交通流的特征.
3 仿真分析 3.1 仿真场景设置在本次搭建的城市交叉口交通流仿真平台,道路场景设置如下:道路为单向4车道,机动车道宽度为3.5 m,非机动车道宽度为4.0 m.当分析电动车数量的影响时,将电动车到达率λN取为0.25;当分析电动车到达率时,将电动车排队数量N取为20辆.将一个绿灯时间内(80 s)的机动车流量与所有机动车通过交叉口的平均速度的仿真结果进行分析与评价.
3.2 排队电动自行车数量影响分析(N)图 4为在逐渐增加电动自行车排队数量情况下80 s机动车交通流量与平均速度(头车平均速度和所有车辆平均速度)变化趋势.由图 4可以看出,当0 ≤ N ≤ 20时,随着电动自行车排队的出现,机动车流量与平均通过速度虽有降低,但是由于此时电动自行车数量还较小,有足够的空间使其通过,所以下降趋势并不明显.当N >20时,由于电动自行车排队数量太大,将占用大量的机动车道路资源.另外,电动车在绿灯开始时由于启动速度较大,一般会行驶在机动车之前,如果电动车数量较大,若不能及时通过交叉口,滞后的电动自行车将对后面的机动车的行驶起阻碍作用,造成后面机动车行驶速度缓慢.因此,不难得出当N从最小值到最大值,机动车流量大概下降18.2%,平均速度下降19.6%.

|
图 4 排队电动自行车数量对机动车数量及平均速度的影响 Figure 4 Influences of the number of queuing electric bicycles on motor vehicles and their average speed |
本文电动自行车到达率λN是指单位时间内电动车的到达数量.通过电动自行车的到达率与交叉口的交通量仿真结果可知,如图 5所示.

|
图 5 电动自行车到达率对机动车的影响 Figure 5 Influences of electric bicycles arrival rate on motor vehicles |
当电动自行车到达率在0 ≤ λN < 0.1时,随着电动自行车到达率的增大,流量与通行速度有明显下降,由此可知电动自行车到达率在一定范围内会对交叉口机动车交通流量产生巨大的影响;当λN ≥ 0.1时,基本趋于稳定,就算λN达到一定值时,由于电动车也是单辆到达,有足够的通行道路资源供其通过,电动自行车驾驶员一般不会行驶进机动车行驶空间.同时可以观察到的是,由于电动自行车到达的增多,靠近电动车辆一侧的机动车驾驶员从安全角度考虑也会降低自身的行驶速度以避免与电动车辆发生擦撞.
4 结论1) 改进了现有的社会力模型,建立了新的机动车-电动车异质交通流模型,可以较为真实地描述机动车与电动车的交通流特性,与道路交通流实际状况较为符合.并且由模型验证结果显示,平均绝对相对误差eMARE较小,所以模型具有比较高的精度.
2) 电动自行车对信号交叉口机动车的行驶干扰较大,当电动自行车排队数量N>20时,机动车总数和车辆平均速度都急剧下降.建议在信号交叉口电动自行车排队数量超过20辆时,应对其进行控制和交通组织来有效缓解交通拥堵和降低交通安全隐患.
3) 通过对电动自行车到达率的分析,其增加基本上不影响机动车的流量和通行速度.
4) 根据研究,提出以下建议:可通过信号控制方式让电动车提前2~3 s的时间行驶或将非机动车停车线提前,以减少与机动车辆的冲突;增加电动自行车专用排队等待区域面积,增加非机动车道宽度;规范电动自行车驾驶员的行为,尽量避免其进入机动车行驶区域.
| [1] |
周钊. 非机动车道的利用率与宽度等影响因素的关系[D]. 成都: 西南交通大学, 2013. ZHOU Zhao. The relationship between the utilization of non-motorized vehicle lane and width and other factors[D]. Chengdu: Southwest Jiaotong University, 2013. |
| [2] |
ZHAO Xiaomei, JIA Bin, GAO Ziyou, et al. Traffic interactions between motorized vehicles and nonmotorized vehicles near a bus stop[J]. Journal of Transportation Engineering, 2009, 135(11): 894-906. DOI:10.1061/(ASCE)TE.1943-5436.0000056 |
| [3] |
JIANG Rui, JIA Bin, WU Qingsong. Stochastic multi-value cellular automata models for bicycle flow[J]. Journal of Physics A: Mathematical and General, 2004, 37(6): 2063. DOI:10.1088/0305-4470/37/6/007 |
| [4] |
XIE Dongfan, GAO Ziyou, ZHAO Xiaomei. Combined cellular automaton model for mixed traffic flow with non-motorized vehicles[J]. International Journal of Modern Physics C, 2010, 21(12): 1443-1455. DOI:10.1142/S0129183110015944 |
| [5] |
GUO Hongwei, GAO Ziyou, ZHAO Xiaomei, et al. Dynamics of motorized vehicle flow under mixed traffic circumstance[J]. Communications in Theoretical Physics, 2011, 55(4): 719. DOI:10.1088/0253-6102/55/4/38 |
| [6] |
贾斌, 高自友, 李克平, 等. 基于元胞自动机的交通系统建模与模拟[M]. 北京: 科学出版社, 2007. JIA Bin, GAO Ziyou, LI Keping, et al. Models and simulation of traffic system based the theory of cellular automaton[M]. Beijing: Science Press, 2007. |
| [7] |
贾宁, 马寿峰. 考虑摩擦干扰的机非混合交通流元胞自动机仿真[J]. 系统仿真学报, 2011, 23(2): 390-393. JIA Ning, MA Shoufeng. Simulation of mixed traffic flow with friction interference using cellular automata[J]. Journal of System Simulation, 2011, 23(2): 390-393. |
| [8] |
贾宁, 马寿峰. 自行车干扰下机动车交通流的元胞自动机模型[J]. 系统工程理论与实践, 2010, 30(7): 1333-1339. JIA Ning, MA Shoufeng. Cellular automata model for the motor-vehicle flow under the interference of bicycles[J]. Systems Engineering-Theory & Practice, 2010, 30(7): 1333-1339. DOI:10.12011/1000-6788(2010)7-1333 |
| [9] |
DIRK H, PETER M. Social force model for pedestrian dynamics[J]. Physical Review E(S1539-3755), 1995, 51(5): 4282-4285. |
| [10] |
BANI A. A mathematical model for driver and pedestrian interaction in shared space environments[C]// Proceedings of the 44th Universities Transport Study Group Conference. Aberdeen: Imperial College London, 2012.
|
| [11] |
TANG T Q, HUANG H J, SHANG H Y. A dynamic model for the heterogeneous traffic flow consisting of car, bicycle and pedestrian[J]. International Journal of Modern Physics C, 2010, 21(2): 159-176. DOI:10.1142/S0129183110015038 |
| [12] |
GIPPS P G. A behavioural car-following model for computer simulation[J]. Transportation Research Part B: Methodological, 1981, 15(2): 105-111. DOI:10.1016/0191-2615(81)90037-0 |
| [13] |
孙若晓. 施工区对城市信号交叉口通行能力影响分析与仿真[D]. 成都: 西南交通大学, 2016. SUN Ruoxiao. A study of the capacity of signalized intersection with work zone based on modeling and simulation[D]. Chengdu : Southwest Jiongtong University, 2016. |
| [14] |
陈大飞. 基于社会力的城市道路混合交通流建模与分析[D]. 长沙: 中南大学, 2011. CHEN Dafei. Modeling and analyzing of mixed traffic flow on the urban road section based on social force[D]. Changsha: Central South University, 2011. |
| [15] |
FEI L, ZHU H B, HAN X L. Analysis of traffic congestion induced by the work zone[J]. Physica A: Statistical Mechanics and its Applications, 2016, 450: 497-505. DOI:10.1016/j.physa.2016.01.036 |
| [16] |
DIRK H, BENNO T. Generalized force model of traffic dynamics[J]. Phys Rev E, 1998, 58(1): 133-138. DOI:10.1103/PhysRevE.58.133 |
| [17] |
GUNAWAN F E. Two-vehicle dynamics of the car-following models on realistic driving condition[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(2): 67-75. DOI:10.1016/S1570-6672(11)60194-3 |
| [18] |
王青燕. 微观交通仿真模型参数标定及检验研究[D]. 济南: 山东大学, 2013. WANG Qingyan. Parameters calibration and test research of microscopic traffic simulation mode[D]. Jinan: Shandong University, 2013. |
| [19] |
MENG Q, WENG J. An improved cellular automata model for heterogeneous work zone traffic[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(6): 1263-1275. DOI:10.1016/j.trc.2011.02.011 |
| [20] |
PUNZO V, SIMONELLI F. Analysis and comparison of microscopic traffic flow models with real traffic microscopic data[J]. Transportation Research Record: Journal of the Transportation Research Board, 2005, 1934(1): 53-63. DOI:10.1177/0361198105193400106 |
| [21] |
PINDYCK R S, RUBINFELD D. Economic models and econometric forecasts[M]. Boston: Irwin/McGraw-Hill, 1998.
|
 2018, Vol. 50
2018, Vol. 50


