2. 宁波大学 建筑工程与环境学院,浙江 宁波 315211;
3. 东南大学 交通学院,南京 210096
2. Faculty of Architectural, Civil Engineering and Environment, Ningbo University, Ningbo 315211, Zhejiang, China;
3. School of Transportation, Southeast University, Nanjing 210096, China
大跨径斜拉桥一般均安装有健康监测系统,以监测结构的变化状态,通过各类传感器数据的获取,分析结构潜在的损伤[1].其中,斜拉索索力是关键测试项之一,它是反映结构整体内力变化状态的重要参数.在斜拉桥运营过程中,由于塔顶偏位、主梁下挠、基础沉降等因素造成结构内力状态改变,进而引起索力重分布[2].因此在斜拉桥运营阶段尤其要关注索力的评估,以掌握结构的安全性能.
目前在规范[3]里索力的评估方法采用的是单索索力的变化率控制指标,当索力变化率大于10%时,判定索力可能异常.该方法中阈值确定较为主观,且无法考虑索力重分布的特性.后来学者们提出了针对群索的评估方法,例如灰色关联度[4-5]、变权综合法[6]、蒙特卡罗法[7]、神经网络法[8]等,这些方法考虑了群索的关联性,然而在应用中也存在一定的劣势,比如忽略了索力的空间特性,评估仅根据某一时间点的一组数据进行,或应用较为复杂或物理意义不明等.
为了能充分利用积累的长期监测数据,对索力的时空特征进行全面描述,以得到一种便于应用推广的群索评估方法,本文以长期监测数据为基础,分析群索的时空特征,并建立群索的综合时空评估方法.以一座运营12 a的大跨径斜拉桥为工程背景,验证本文方法的可行性与适用性.
1 群索的时空评估方法 1.1 索力的时空评估群索的评估针对的是时间和空间的综合体现,分别由时间指标R1和空间指标R2决定.本文借鉴风险评估中的基于ALARP的桥梁风险矩阵决策方法[9],该方法是最常用且被普遍接受的定性风险分析方法.它是通过将风险事故发生的概率和风险损失置于一个矩阵中进行风险水平决策.在群索的综合评估中,将时间指标R1和空间指标R2置于一个矩阵中进行评估决策.评估等级分为四级,分别为蓝色Ⅰ级、黄色Ⅱ级、橙色Ⅲ级和红色Ⅳ级.具体见表 1,时间指标划分为1级至4级4个级别,分别代表一般、较大、重大和特大,空间指标划分为1级至4级,分别代表较好、轻微严重、较严重和特别严重.
| 表 1 时空评估等级评定标准 Table 1 Rating criteria for temporal and spatial evaluation |
针对每根索进行评定,然后可以绘制相应的索力分布评估图.对于处于橙色及以上的斜拉索,需要进一步的现场检测、检查.
1.2 时间指标的确定从时间尺度来看,反映索力变化特征的是索力的变化速率和变化幅度,而两者的计算都依赖于恒载索力.监测索力中最主要的环境影响成分是温度和车辆荷载,温度引起的索力变化具有季节性特点[10],车辆荷载引起的索力变化具有不规则变动特性,这与时间序列[11]的特点较为接近.因此可通过时间序列分析将恒载索力趋势项提取出来.
假设在某段时间内的索力监测样本为一组含n个变量的有序观测值,y1, y2, …, yn,那么监测值Yt可表达为
| $ {Y_t} = {T_t} + {S_t} + {R_t},t = 1,2, \ldots n. $ | (1) |
式中Tt为趋势项,St为季节项,Rt为随机项.
趋势项估计可采用一元线性回归模型[12],设yi=a+bt+εi, t=1, 2, …, n,Y=(y1, y2, …, yn)T,
| $ {\left( {\hat a,\hat b} \right)^{\rm{T}}} = {\left( {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{T}}}} \right)^{ - 1}}\mathit{\boldsymbol{ZY}}. $ | (2) |
其中
而索力变化幅度也可通过索力变化率绝对值计算出来,定义索力变化幅度为
| $ k = \frac{{\left| {{y_n} - {y_1}} \right|}}{{{y_1}}} \times 100\% . $ | (3) |
索力变化幅度的阈值设定按拉索自身强度及相关文献[13]建议,设为40%. 表 2给出了时间评估指标的评估等级标准.
| 表 2 时间评估指标的等级评定标准 Table 2 Rating criteria for time assessment indexes |
从空间尺度上来看,一般大跨径斜拉桥采用双索面形式,且多为两塔及以上,因此斜拉索具有空间效应.为了考虑偏载、单索的损伤造成两侧索力的偏差过大的情况,需利用合适的指标来反映两组向量之间的相关性,在实际工程中,常用指标有皮尔逊相关系数、欧氏距离、街区距离、Canberra距离,切比雪夫距离等,本文选取分类能力最好的Canberra距离[14]来反映两侧索力的相关性,设上游、下游索力向量分别为{Ui}、{Vi},则Canberra距离表示为
| $ d = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\left| {{u_i} - {v_i}} \right|}}{{{u_i} + {v_i}}}} . $ | (4) |
式中m为上游索力监测样本数量. 0≤d≤1,d越接近于0,则上下游索力变化越一致.
对索力的空间评估指标等级评定标准制定如下:当d≤0.025时,R2为1级,当0.025 < d≤0.05时,R2为2级,当0.05 < d≤0.08时,R2为3级,当d>0.08时,R2为4级.
2 实例验证 2.1 工程概况南京长江第三大桥(简称“南京三桥”)是上海至成都国道(GZ55)主干线的重要组成部分.主桥双塔双索面钢塔钢箱梁斜拉桥,主跨648 m,全长1 288 m.全桥共设8×21对高强度平行钢丝外挤包高密度聚乙烯斜拉索,最小型号为7×109,最大型号为7×241.南京三桥于2005年10月建成,该桥斜拉索布置外观效果图见图 1.

|
图 1 主桥斜拉索布置效果图 Figure 1 Layout of the stay cable on the main bridge |
为保障南京三桥运营阶段健全性监测、评估及维护决策的要求,保证桥梁的安全运营,在主桥上安装了桥梁结构健康监测系统,每个拉索均布置有压力传感器[15].
由于拉索数量众多,需要对其进行编号.根据桥梁南北走向和上下游河道的特点,编号包含了3个字母和一个数字.第一个为S或N,分别代表南塔或北塔,第二个为J或A,代表为江侧或岸侧,第三个为S或X,代表上游或下游,最后一个为1至21,代表最短索至最长索.例如,SJS15表示为南塔江侧上游15号拉索.
由于长索的振动频率比短索低,更易发生不利的振动损伤,出现的病害概率较高,因此对于长索的观测具有重要意义,进而本文主要以长索的索力分析为主.选取上游侧最长的17号至21号共20根斜拉索索力为研究对象.
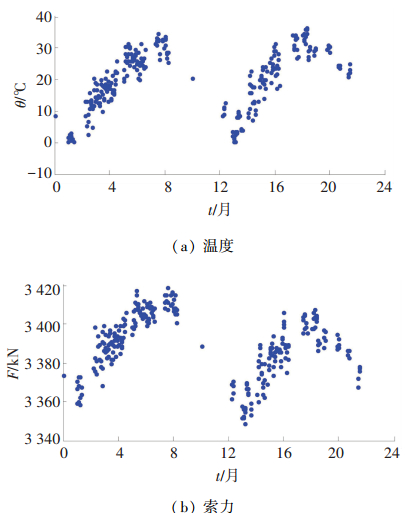
2.2 索力的时空特征与评估1) 索力的时间指标.以SJS17索为例,图 2给出了该索2008年~2009年两年的温度和索力数据,可以看出,索力与温度有极强的相关性,相关系数高达0.96.采用一元线性回归方法,计算该索的时间评估指标.
|
图 2 SJS17索2008年—2009年两年的索力和温度数据 Figure 2 Cable force and temperature data of SJS17 cable from 2008 to 2009 |
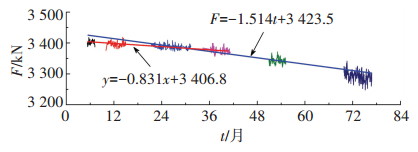
选取数据段为2006年5月到2012年8月,首先通过时间序列分析得到恒载索力趋势项,然后分别计算76个月和前38个月的数据线性拟合结果,得到各自拟合的斜率分别为-1.514和-0.831,如图 3所示,得到γ=
|
图 3 SJS17号2006—2012年的索力数据及线性拟合结果 Figure 3 Cable force data and linear fitting results of SJS17 cable in 2006—2012 |
根据表 2确定其时间指标为2级.然后依照该方法得到其他索的时间指标.
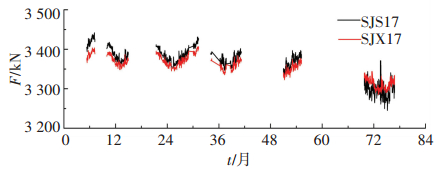
2) 索力的空间分布.对于SJS17和SJX17拉索的数据,如图 4所示,上下游索力变化趋势保持较好的一致性,计算其Canberra距离d=0.002.查空间指标评定标准确定其空间指标为1级.以此方法可以得到其他索的空间指标.
|
图 4 SJS17和SJX17索2006年-2012年的索力数据 Figure 4 Cable force data for SJS17 and SJX17 in 2006~2012 |
最后,查表 1,得到SJS17索的时空综合等级为中度Ⅱ级.
2.3 群索综合评估结果及分析其他19根拉索的评估结果见表 3,其中SAS20索、SAS18索、SJX18索和NAX20索出现故障,因此相应的数据缺失,有效结果为18根索.表中,k为索力变化幅度,γ为索力变化速率比,d为Canberra距离.从表 3中可以看出,18根索的时空综合等级分布Ⅰ至Ⅲ级之间,其中Ⅲ级的拉索有1根(NAS19号拉索),该拉索与下游索力变化具有较大差异性,需进一步的检查;Ⅱ级的拉索有12根,这些拉索普遍时间评估等级较高,这是由索力指数级的增长或下降造成的,养护人员需密切观察索力的变化,并检查相应拉索索体锈蚀断丝状况.将评估等级形成索力的评估等级图,如图 5所示,可以更加清晰地看出索力的状况,便于养护人员进行更有针对性的拉索检查.
| 表 3 20根典型长索的时空评估等级 Table 3 Temporal and spatial evaluation rate of 20 typical long stay cables |
|
图 5 20根典型长索的时空评估结果分布 Figure 5 Temporal and spatial evaluation result distribution of 20 typical long stay cables |
1) 以南京三桥的上游20根长索的7 a监测数据为样本,进行时空综合评估.监测索力符合时间序列特性,可采用一元线性回归模型提取趋势项,并考虑索力变化幅度,作为索力的时间评估指标;索力通常具有空间特性,取两侧索力的Canberra距离作为空间评估指标.
2) 群索的评估是时间和空间的综合体现,借鉴风险评估中的基于ALARP的桥梁风险矩阵决策方法,将时间指标和空间指标置于一个矩阵中进行综合评估,评估等级分为4级.
3) 评估样本中斜拉索的时空综合等级在Ⅱ级及以上的主要原因有索力变化趋势过快、上下游索力差异较大,评估分布图给养护人员提供更有针对性的拉索外观检查.
| [1] |
XU Zhaodong, ZENG Xin, LI Shu. Damage detection strategy using strain-mode residual trends for long-span bridges[J]. Journal of Computing in Civil Engineering, 2015, 29(5): 4014064-1. DOI:10.1061/(ASCE)CP.1943-5487.0000371 |
| [2] |
MARTINS A M B, SIMÕES L M C, NEGRÃO J H J O. Optimum design of concrete cable-stayed bridges[J]. Engineering Optimization, 2016, 48(5): 772. DOI:10.1080/0305215X.2015.1057057 |
| [3] |
交通运输部公路科学研究院.公路桥梁技术状况评定标准: JTG/T H21-2011[S].北京: 人民交通出版社股份有限公司, 2011 China Academy of Transportation Sciences.Standards for technical condition evaluation of highway bridges: JTG/T H21-2011[S]. Beijing: China Communications Press Co., Ltd., 2011 |
| [4] |
刘小玲, 黄侨, 任远, 等. 大跨度钢斜拉桥主梁监测挠度的评估与预警[J]. 湖南大学学报(自然科学版), 2016, 43(9): 98. LIU Xiaoling, HUANG Qiao, REN Yuan, et al. Assessment and early warning on the monitoring girder deflection of the long-span steel cable-stayed bridge[J]. Journal of Hunan University (Natural Sciences), 2016, 43(9): 98. DOI:10.3969/j.issn.1674-2974.2016.09.013 |
| [5] |
钟桔.斜拉桥拉索损伤状态的有限元模拟与模型试验研究[D].长沙: 湖南科技大学, 2014 ZHONG Ji. Finite element simulation and model test study on cable damage state of cable stayed bridge[D]. Changsha: Hunan University of Science and Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10534-1015015794.htm |
| [6] |
白焱, 张志峰. 采用模糊云模型的武器研制项目风险传导评估[J]. 哈尔滨工业大学学报, 2016, 48(10): 168. BAI Yan, ZHANG Zhifeng. Risk conduction assessment of weapon development projects by using fuzzy cloud model[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 168. DOI:10.11918/j.issn.0367-6234.2016.10.025 |
| [7] |
杨晓艳, 贡金鑫, 张启伟. 随机车辆荷载作用下斜拉索索力的概率模型及可靠度分析[J]. 建筑科学与工程学报, 2014, 31(2): 90. YANG Xiaoyan, GONG Jinxin, ZHANG Qiwei. Analysis of probabilistic model of stay cable stress and reliability under random vehicle loads[J]. Journal of Architecture and Civil Engineering, 2014, 31(2): 90. DOI:10.3969/j.issn.1673-2049.2014.02.016 |
| [8] |
ARANGIO S, BONTEMPI F. Structural health monitoring of a cable-stayed bridge with Bayesian neural networks[J]. Structure & Infrastructure Engineering, 2015, 11(4): 575. DOI:10.1080/15732479.2014.951867 |
| [9] |
WANGWEI, HU Chuanbo, CHEN Nengcheng, et al. Spatio-temporal enabled urban decision-making process modeling and visualization under the cyber-physical environment[J]. Science China Information Sciences, 2015, 58(10): 1. DOI:10.1007/s11432-015-5403-x |
| [10] |
熊文, 涂雪, 肖汝诚. 基于变异系数与趋势因子的斜拉桥索力评估[J]. 同济大学学报(自然科学版), 2011, 39(11): 1575. XIONG Wen, TU Xue, XIAO Rucheng. Condition assessment of stay cable forces based on variation and trend coefficients[J]. Journal of Tongji University(Natural Science), 2011, 39(11): 1575. DOI:10.3969/j.issn.0253-374x.2011.11.003 |
| [11] |
LI Xingxin, REN Weixin, BI Kaiming. FBG force-testing ring for bridge cable force monitoring and temperature compensation[J]. Sensors and Actuators A-Physical, 2015, 223(3): 105. DOI:10.1016/j.sna.2015.01.003 |
| [12] |
VAN LE H, NISHIO M. Time-series analysis of GPS monitoring data from a long-span bridge considering the global deformation due to air temperature changes[J]. Journal of Civil Structural Health Monitoring, 2015, 5(4): 415. DOI:10.1007/s13349-015-0124-9 |
| [13] |
WENG Lina, ZHANG Ping, FENG Zhiyong, et al. Short-term link quality prediction using nonparametric time series analysis[J]. Science China Information Sciences, 2015, 58(8): 1. DOI:10.1007/s11432-014-5270-x |
| [14] |
DAN Danhui, ZHAO Yiming, YANG Tong, et al. Health condition evaluation of cable-stayed bridge driven by dissimilarity measures of grouped cable forces[J]. International Journal of Distributed Sensor Networks, 2013, 2013(2013): 818967-1. DOI:10.1155/2013/818967 |
| [15] |
LIU Xiaoling, HUANG Qiao, REN Yuan. Anomaly detection algorithm for stay cable monitoring data based on data fusion[J]. Journal of Harbin Institute of Technology (New Series), 2016, 23(3): 39. DOI:10.11916/j.issn.1005-9113.2016.03.003 |
 2018, Vol. 50
2018, Vol. 50


