2. 广东省交通规划设计研究院股份有限公司,广州 510507;
3. 广州市交通委员会,广州 510620
2. Guangdong Province Communications Planning and Design Institute Co., Ltd., Guangzhou 510507, China;
3. Communications Commission of Guangzhou Municipality, Guangzhou 510620, China
实时掌握城市交通枢纽、各大旅游景点的人流量状况,为城市交通规划、重点区域安全保障以及大型活动安保资源配备提供数据支撑,已受到社会广泛关注也是交通信息化建设的重要组成部分[1].相比于传统区域人流量获取方法,如人工计数法[2]和视频检测法[3],基于手机信令数据的人流量获取方法具有成本低、覆盖广以及能够适应复杂环境等优点[4-6].目前国内外针对手机信令数据的研究主要集中于居民出行轨迹链识别与出行OD提取,文献[7]运用仿真系统模拟现实环境的手机网络,仿真获取交通出行OD和相应道路的流量数据;文献[8]通过手机信令数据推导出居民出行表,进而构建了跨城市范围的交通规划模型;文献[9]定义夜间停留最频繁的点为居住地,停留次数与离家距离乘积最大的点为工作地,生成了代表性的起始目的地矩阵;文献[10]通过车辆行驶里程数来验证了手机信令数据用于居民出行特性的研究具有较好的准确性;文献[11]根据手机信令定位数据和话单数据获取了出行时耗、出行距离等出行特征;文献[12]通过分析居住地所对应的手机基站位置结合个体活动序列,运用模拟手段实现了对居住地标识;文献[13]利用手机信令数据识别上海市域内手机用户的工作地和居住地,获取就业者通勤数据.
综上,国内外根据手机信令数据获取区域人流量的研究还较少,受设计和管理单位委托,本文构建了基于手机信令数据的城市交通枢纽区域人流量智能化统计方法;分析了广州火车站近两年春运人流聚集特性;建立了基于平均绝对百分比误差最小的k值自适应计算模型;设计了基于改进的k近邻算法区域人数短时预测算法;实现了对广州火车站区域人群聚集情况的连续监测与预测.本文的研究对科学控制区域人数,预防区域人群过度拥挤,防止群体性安全事故发生,保障重点区域安全有着积极意义.
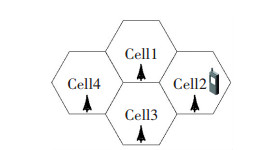
1 手机信令数据获取 1.1 手机信令数据产生原理运用手机定位进行交通信息采集的方法主要有起源蜂窝小区定位(COO)、基于到达时间差的定位(TDOA)、GPS辅助定位(A-GPS)和前向链路三角定位法(AFLT)等[14-15].其中利用蜂窝小区定位的方法不需要在基站或者手机加装设备,而是通过接收移动通信网络自身运作所产生的信令数据,成本低且容易推广,因此也是国内基于手机信令进行交通调查的主要技术手段.其原理如图 1所示.
|
图 1 蜂窝小区定位示意图 Figure 1 Cell positioning diagram |
蜂窝小区为正六边形,是信令记录中产生位置信息的基本单元,一定数量的蜂窝小区构成了位置区.每个蜂窝小区都有唯一的小区编号CGI,由为位置区识别码和小区识别代码组成.
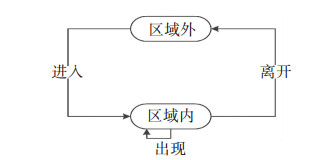
1.2 手机信令数据映射至研究区域通过记录手机用户发生的通信事件,可识别该用户所处区域,如图 2所示.同时本文对部分手机用户行为进行了定义:区域外,指用户不在研究区域;区域内,指用户在研究区域;离开,指原本在区域内的用户在该区域外发生了通信事件,则称为离开;出现,指用户在区域内发生通信事件,则称用户在该区域出现,首次出现在区域内则称为进入.手机信令数据虽然显示了数据点的位置信息,但无法直观地展现出用户在具体哪个区域.因此本文运用ArcGIS10.2将信令定位数据映射至具体区域,便于计算和分析区域人流量.
|
图 2 手机信令数据区域状态跃迁图 Figure 2 Mobile phone signaling data area state transition |
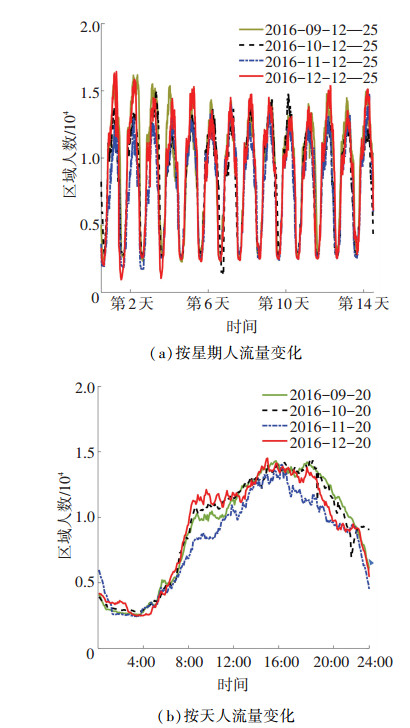
城市交通枢纽区域人流量往往随时间呈现出一定规律性.本文选取了广州火车站枢纽2016年9月—12月数据进行分析,结果如图 3所示.
|
图 3 广州火车站日人流量变化 Figure 3 Daily traffic changes in Guangzhou Railway Station |
人流量时间序列指人流量数据按时间先后顺序排列而成的数列.由图 3(a)可得,广州火车站区域人流量每日的变化趋势基本一致,日人流量变化呈现出先下降后上升再下降的变化规律,具体来看,每天有一个波谷与一个波峰,波谷出现在3:30—4:30时之间,波峰出现在16:00时左右,如图 3(b)所示.总体而言,城市交通枢纽区域人流量时间序列呈现出较为明显的周期性变化特点,基于此本文将通过对传统的k近邻算法进行优化,实现区域人数预测.
3 基于手机信令数据的城市交通枢纽人流预测 3.1 k近邻算法预测原理k近邻算法由Cover和Hart提出,作为一种基于统计的非参数回归方法,被广泛应用于多个领域[16-19].其主要思想是通过在大量样本中查找与当前状态相似度最高的历史数据,并把最相似的历史状态应用于当前预测.
对于随机向量(X, Y),若x∈Rd,将(X1, Y1), (X2, Y2), …, (Xn, Yn)按照‖Xi-x‖的值从小到大依次排序,将得到的新排列序记为((X(1, n), Y(1, n)), (X(2, n), Y(2, n)), …, (X(n, n), Y(n, n))),X(k, n)为x的第kn位近邻,kn表示近邻数k是随着样本点个数n变化的. k近邻算法函数定义为
| $ {m_n}\left( x \right) = \frac{1}{{{k_n}}}\sum\nolimits_{i = 1}^{{k_n}} {{Y_{(i, n)}}\left( x \right).} $ | (1) |
同时,当存在多个近邻与x之间距离相同时,可假设此时若i < j,则‖Xi-x‖ < ‖Xj-x‖,进而避免‖Xi-x‖=‖Xj-x‖.
此外,在文献[20]中对k近邻算法的相合性与收敛性根据Stone定理已证明.
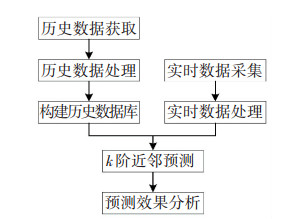
3.2 基于k值自适应的城市交通枢纽人流量预测基于手机信令数据的交通枢纽人流量k近邻预测算法基本流程如下:首先运用Oracle软件搭建具有较大样本量的交通枢纽人流量数据库,并且实现数据的不断更新;其次根据交通枢纽人流量特性设计k近邻模型的状态向量;然后根据距离度量方式和自适应k值计算模型构成算法的搜索机制;接着输入的当前数据,利用预测算法得到下一时刻的人流量;最后对预测效果进行评价,如图 4所示.
|
图 4 算法流程图 Figure 4 Flow chart of algorithm process |
算法核心内容包括:状态向量设计、距离度量方式构建、k值的确定和预测算法等4个方面.
1) 状态向量设计.状态向量作为当前状态与历史状态比较的标准,本文通过预测日当天实时数据挖掘得到的人流变化规律在已构建的历史数据库中寻找其近邻,从而预测下一时间点人流量,状态向量为
| $ {F_n} = ({x_{n1}}, {x_{n2}}, ..., {x_{nt}}). $ | (2) |
式中:n为预测日前第n天,n取0时表示预测日当天,xnt为预测日前第n天t时刻的客流量.
2) 距离度量方式构建.为了实现对当前数据与数据库中样本数据之间近似程度的度量,本文采用欧式距离作为度量指标.记预测日的信令向量为xi=(xi(1), xi(2), ..., xi(n))T(以5 min为时间间隔),历史数据的信令向量为hj=(hj(1), hj(2), ..., hj(n))T.由已知的预测日的部分元素xi=(xi(1), xi(2), ..., xi(n))T,可计算xi,hj的Lij距离为
| $ {L_{ij}}({x_i}, {h_j}) = (\sum\limits_{l = 1}^n {{{\left| {{x_i}^{(l)} - {h_j}^{(l)}} \right|}^2}{)^{\frac{1}{2}}}.} $ | (3) |
3) 自适应k值计算.模型k值作为从数据库中选取的近邻个数的参数,对预测结果有着重大影响.目前国内外关于k值的确定办法主要是针对各自研究问题,在比较不同k值的计算结果下进而择优选择.本文在大量基础数据分析基础上,构建基于平均绝对百分比误差最小的k值自适应计算模型为
| $ {k_m} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i}{\rm{ - }}{y_i}}}{{{y_i}}}} \right|, } $ | (4) |
| $ K = {\rm{Min}}\left\{ {{k_1}, {k_2}, {k_3}...{k_m}} \right\}. $ | (5) |
式中:yi为实际值,
4) 预测算法.预测算法是根据搜索得到的k组近邻值数据预测下一时刻区域人流量.预测区域人数xi(t+1)为
| $ {x_i}^{(t + 1)} = \frac{{L_{ij}^{ - 1}}}{{\sum\limits_{i = 1}^k {L_{ij}^{ - 1}} }}{h_j}^{(t + 1)}. $ | (6) |
式中:hj(t+1)为历史数据库中搜索到的第j个近邻所对应的t+1时刻的人流量,Lij为当前数据与第j个近邻的距离.
3.3 预测效果评价为了对模型的预测效果进行客观评价,本文以平均绝对百分比误差与均方百分比误差作为模型的效果评价指标,其计算分别公式为
| $ {P_{{\rm{MAPE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|, } $ | (7) |
| $ {P_{{\rm{MSP}}}} = \sqrt {\frac{{{{\sum\limits_{i = 1}^n {\left( {\frac{{{{\hat y}_i}{\rm{ - }}{y_i}}}{{{y_i}}}} \right)} }^2}}}{n}} . $ | (8) |
式中:PMAPE为平均绝对百分比误差,PMSP为均方百分比误差,yi为实际值,
PMAPE与PMSP表示了预测的可靠性程度和相对平均偏离程度,两者数值越小,则说明预测可靠性程度越高且预测相对偏离程度越低.
4 预测实例分析 4.1 基于手机信令数据的广州火车站春运人流分析广州是全国春运压力最大的地区之一,广州火车站作为广州地区春运最重要的节点,在历年春运中均为全国关注焦点. 2008年受南方冰雪灾害影响造成广州火车站及周边区域最大滞留旅客数超过40万,2016年受北方雨雪影响造成最大滞留旅客数近10万.本文基于广州市手机信令定位数据分析了火车站区域近两年春运期间人流变化情况. (2016年春运为2016年1月24日—3月3日,2017年春运为2017年1月13日—2月21日.)
由图 5可得,2016年春运期间每日区域人数分布特点主要有:总体上春运期间区域内每天人数均呈现出先上升后下降趋势,且每天人数波动范围较大,同时春节前区域每日人数要远高于春节后(本文春节指春节假期,2016年为2月7日—2月13日;2017年为1月27日—2月2日),此外春运40 d大致可以分为3个阶段,第1阶段为春运开始到春节前(15 d),第2阶段为春节期间(7 d),第3阶段为春节后到春运结束(18 d),第1阶段每天区域人数聚集较多时段主要在12:00—19:00时之间,并随着时间越接近春节,区域聚集人数持续在高位的时间逐渐延长,在春运第10天时高值持续时间从9:00点—23:00时,此后开始缩小.第2阶段区域每天各时段人数分布较为均匀且人数较少,第3阶段区域内每天人数逐渐开始增大,一天中人数较大值主要出现在15:00—18:00时之间.

|
图 5 2016年春运广州火车站区域人数统计 Figure 5 Regional population in Guangzhou Railway Station during 2016 Spring Festival |
由图 6可得,2017年春运期间每日区域人数分布情况同2016年相同,仍划分为3个阶段,总体上3个阶段每天均呈现出聚集人数先上升后下降的趋势,但每天人数波动范围较2016年春运要小,具体而言,第1阶段每天区域人数聚集相对较多时段主要在12:00—23:00之间,持续时间较长但人数峰值不大,第2阶段区域每天各时段人数分布较为平均且人数较少,第3阶段,聚集人数逐渐增加,但一天中增长变化趋势较为平缓.

|
图 6 2017年春运广州火车站区域人数统计 Figure 6 Regional population in Guangzhou Railway Station during 2017 Spring Festival |
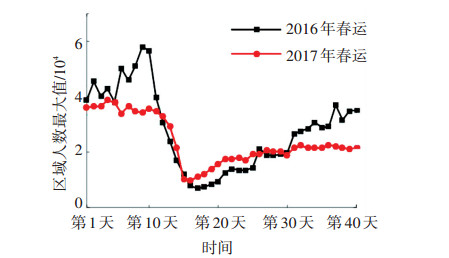
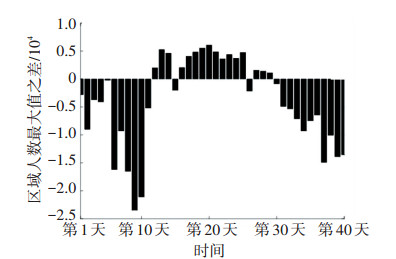
近两年春运区域人数每日最大值分布如图 7所示,总体上看2016年春运期间日峰值人数分布呈现出先波动式上升,在春运第9天达到最高值达到57 965人,此后持续下降,在春运第17天达到最低值6 957人,之后呈现出波动回升趋势.相比之下,2017年春运期间日峰值人数分布变化趋势较为平缓,变动幅度较小,春运前10 d基本处于3.2万到4万人之间的小幅波动中,此后人数逐渐下降,在春运第16天达到最低值9 800人,此后呈现出缓慢回升趋势.出现两年情况波动不完全相同的原因,主要在于2016春运期间受到天气影响导致广州火车站较多列车晚点,出现了大面积旅客滞留状况的发生,而2017年春运期间各趟列车运行良好未出现晚点.进一步对比得到图 8,2016年春运区域内每日人数峰值高于2017年的天数有24 d,占总天数的60%,主要集中于春运开始阶段(春运前11 d)与春运后期(春运结束前11 d),而日峰值人数2017年较大的时间段主要集中于春节前后,同时日峰值人数差值最大的达到23 460人,发生在春运第9天.
|
图 7 两年春运区域人数每日最大值分布 Figure 7 Maximum number of daily distribution of the number of people during recent two Spring Festivals |
|
图 8 两年春运区域人数每日最大值之差比较 Figure 8 Comparison of the daily maximum number of people during recent two Spring Festivals |
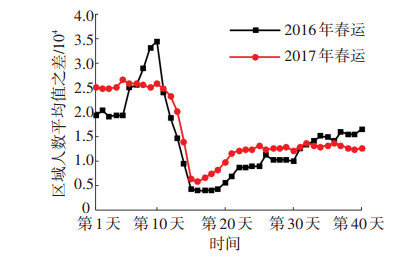
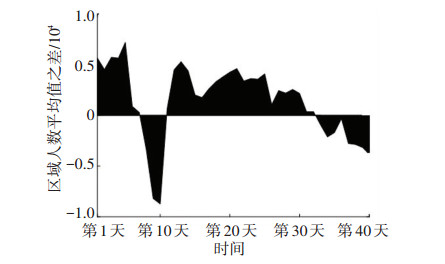
与区域人数最大值分布相比,近两年春运区域人数日均值呈现出相同的规律如图 9所示,2016年春运区域人数日均值先上升后下降再上升而2017年则是先平稳波动后下降再上升.进一步分析可得,2016年春运区域内日均人数高于2017年的天数仅有11 d,占总天数的27.5%,主要集中在春运末期,相反2017年春运区域日均人数有29 d超过2016年.区域人数日均值最大差值达8 731人,在春运第10天.此外通过对图 10进一步分析,发现上半部分面积之和大于下半部分面积之和,由此可以得出2017年春运期间广州火车站枢纽区域人流量大于2016年春运.
|
图 9 两年春运区域人数每日平均值分布 Figure 9 Daily average distribution of the number of people during recent two Spring Festivals |
|
图 10 两年春运区域人数每日平均值之差比较 Figure 10 Comparison of the daily average number of people during recent two Spring Festivals |
以广州市火车站交通枢纽为研究区域,构建火车站交通枢纽客流数据库(手机信令数据来源于与中国移动等通讯商合作项目),实例中选取2017年1月19日作为预测日,通过基于平均绝对百分比误差最小的k值自适应模型计算得图 11.
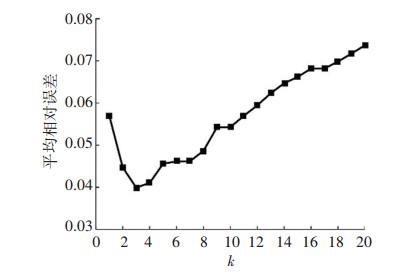
|
图 11 k值的选取 Figure 11 Selection of k value |
从图 11中可以发现平均绝对百分比误差与k值之间的关系不是简单的单调关系,而是总体上随着k值的增加,误差先减小,进一步增加k值,误差k逐渐增大,期间伴随着小幅度波动,k取值过大或过小都会影响预测的精度. k=1~3时,平均绝对百分比误差由5.70%降到3.99%,预测精度提高了30%,预测精度显著提高;而k=3~20时,平均绝对百分比误差由3.99%上升到7.37%,预测精度大幅度下降.进一步对k=3时每个预测点数据进行分析,如图 12,可发现在预测的19日数据中,误差小于4%的约占58%,其中小于2%超过35%,4%到10%约占29%,误差超过10%仅有8%左右.
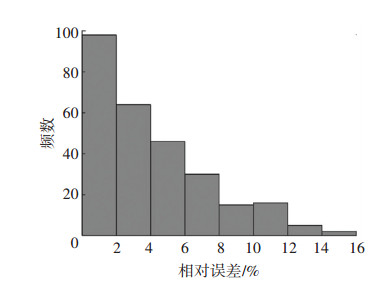
|
图 12 k =3时预测误差频数分布 Figure 12 Frequency distribution of prediction error when k=3 |
图 13为2017年1月16日—1月19日(节假日)预测效果,由图可见,本文构建的预测算法针对节假日的预测能够有较好效果,预测过程中算法对区域人流量的变化较为敏感,能够根据实时数据的变化及时调整预测走势.进一步分析数据得表 1,从表中可以发现,算法在节假日的预测过程中全天平均绝对百分比误差小于6%,算法整体上具有较高的预测精度,具体而言如1月19日,当天预测k取3,全天平均绝对百分比误差为0.039 9,均方百分比误差为0.052 44.
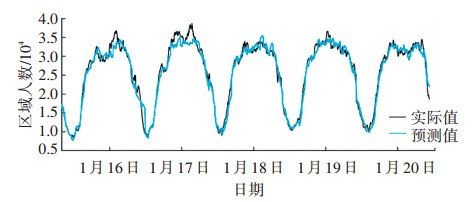
|
图 13 预测值与实际值比较 Figure 13 Comparison of predicted and actual value |
| 表 1 算法预测效果分析(节假日) Table 1 Analysis of algorithmic prediction effect(weekends) |
为了进一步验证预测算法的适用性与准确性, 本文另选取了2016年10月24日—10月30日作为非节假日进行预测,预测效果如图 14,图中预测曲线与实际值吻合度较高,算法预测过程中全天平均绝对百分比误差小于5%(见表 2),与节假日预测相比,其精度更高,主要是由于非节假日历史数据库更为完善.具体来看,如10月26日通过计算得到k值为4时对当天预测具有更优效果,全天平均绝对百分比误差为0.034 3,均方百分比误差为0.044 9.
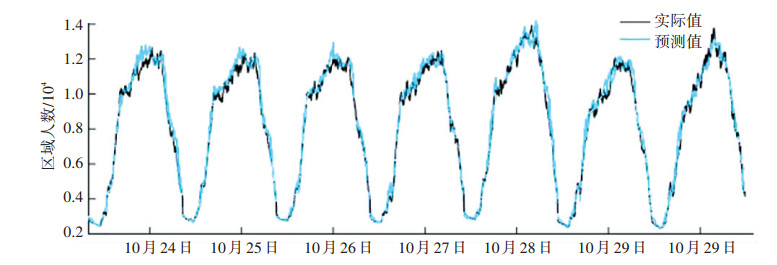
|
图 14 预测值与实际值比较(2016-10-24—2017-10-30) Figure 14 Comparison of predicted and actual value(2016-10-24—2017-10-30) |
| 表 2 算法预测效果分析(非节假日) Table 2 Analysis of algorithmic prediction effect(weekdays) |
总体而言,本文建立的预测算法对区域人流量预测时无论是节假日还是非节假日都能够较好的适应,具有较高的预测精度.
5 结论1) 通过对海量手机信令数据进行处理,结合地理信息系统将手机信令数据映射至所研究区域,实现了对城市交通枢纽区域人流量的实时统计,并分析了广州市火车站区域近两年春运人流量情况.
2) 针对区域人流量存在周期性变化特点,构建了基于平均绝对百分比误差最小的k值自适应计算模型,通过改进的k近邻算法实现了区域人流量短时预测.
3) 以广州市火车站枢纽区域为对象,对节假日与非节假日两种不同交通模式进行算法测试,结果表明所建立的预测模型平均绝对百分比误差在6%以内,能够较为准确地对区域人流量进行短时预测.
4) 有效获取了重点区域人流量状况,可为区域人流疏运准备与群体性安全事故预防提供支撑.下一步研究将主要集中于对异常天气、突发事件等情况下的预测方法的改进.
| [1] |
陈云钢, 刘家彬, 郭正兴, 等. 装配式剪力墙水平拼缝钢筋浆锚搭接抗震性能试验[J]. 哈尔滨工业大学学报, 2013, 45(6): 83. CHEN Yungang, LIU Jiabin, GUO Zhengxing, et al. Test on seismic performance of precast shear wall with reinforcements grouted in holes and spliced indirectly in horizontal connections[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 83. |
| [2] |
王嘉悦, 翁文国, 张小乐. 基于互相关算法的人员密集场所人群运动速度特征研究[J]. 中国安全生产科学技术, 2014, 10(6): 5. WANG Jiayue, WENG Wenguo, ZHANG Xiaole. Empirical study of the characteristics of the pedestrians' velocity in crowded places based on cross-correlation algorithm[J]. Journal of Safety Science and Technology, 2014, 10(6): 5. |
| [3] |
时增林, 叶阳东, 吴云鹏, 等. 基于序的空间金字塔池化网络的人群计数方法[J]. 自动化学报, 2016, 42(6): 866. SHI Zenglin, YE Yandong, WU Yunpeng, et al. Crowd counting using rank-based spatial pyramid pooling network[J]. Acta Automatica Sinica, 2016, 42(6): 866. |
| [4] |
GARCIA J, GARDEL A, BRAVO I, et al. Directional people counter based on head tracking[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3991. DOI:10.1109/TIE.2012.2206330 |
| [5] |
SCHLAICH J, OTTERSTATTER T, FRIEDRICH M. Generating trajectories from mobile phone data[C]// Transportation Research Board Annual Meeting. Washington DC: [s.n.], 2010
|
| [6] |
唐小勇, 周涛, 陆百川. 基于手机信令的大范围人流移动分析[J]. 重庆交通大学学报(自然科学版), 2017, 36(1): 82. TANG Xiaoyong, ZHOU Tao, LU Baichuan. Analysis of wide range population flow analysis based on mobile phone signaling[J]. Journal of Chongqing Jiaotong University(Natural Sciences), 2017, 36(1): 82. |
| [7] |
CACERES N, WIDEBERG J P, BENITEZ F G. Deriving origin destination data from a mobile phone network[J]. Intelligent Transport Systems IET, 2007, 1(1): 15. DOI:10.1049/iet-its:20060020 |
| [8] |
GUR Y J, BEKHOR S, SOLOMON C, et al. Intercity person trip tables for nationwide transportation planning in israel obtained from massive cell phone data[J]. Transportation Research Record Journal of the Transportation Research Board, 2009, 2121(2121): 145. |
| [9] |
TOOLE J L, COLAK S, STURT B, et al. The path most traveled: travel demand estimation using big data resources[J]. Transportation Research Part C, 2015, 58: 162. DOI:10.1016/j.trc.2015.04.022 |
| [10] |
CALABRESE F, DIAO M, LORENZO G D, et al. Understanding individual mobility patterns from urban sensing data: a mobile phone trace example[J]. Transportation Research Part C, 2013, 26(1): 301. |
| [11] |
冉斌. 手机数据在交通调查和交通规划中的应用[J]. 城市交通, 2013, 11(1): 32. RAN Bin. Use of cellphone data in travel survey and transportation planning[J]. Urban Transport of China, 2013, 11(1): 32. |
| [12] |
许宁, 尹凌, 胡金星. 从大规模短期规则采样的手机定位数据中识别居民职住地[J]. 武汉大学学报(信息科学版), 2014, 39(6): 750. XU Ning, YIN Ling, HU Jinxing. Identifying home-work locations from short-term, large-scale, and regularly sampled mobile phone tracking data[J]. Geomatics and Information Science of Wuhan University, 2014, 39(6): 750. |
| [13] |
丁亮, 钮心毅, 宋小冬. 上海中心城就业中心体系测度——基于手机信令数据的研究[J]. 地理学报, 2016, 71(3): 484. DING Liang, NIU Xinyi, SONG Xiaodong. Measuring the employment center system in Shanghai central city: A study using mobile phone signaling data[J]. Acta Geographica Sinica, 2016, 71(3): 484. |
| [14] |
李传华, 孙礼军, 陆林涛. GPS手机的差分定位系统研究[J]. 测绘科学, 2012, 37(3): 28. LI Chuanhua, SUN Lijun, LU Lintao. Differential positioning system base on GPS phone[J]. Science of Surveying and Mapping, 2012, 37(3): 28. |
| [15] |
张国生, 高博, 姚慧敏. 手机定位服务与电子地图[J]. 测绘科学技术学报, 2007, 24(3): 216. ZHANG Guosheng, GAO Bo, YAO Huimin. Location based service and electronical map[J]. Journal of Geomatics Science and Technology, 2007, 24(3): 216. DOI:10.3969/j.issn.1673-6338.2007.03.018 |
| [16] |
王翔, 陈小鸿, 杨祥妹. 基于k最近邻算法的高速公路短时行程时间预测[J]. 中国公路学报, 2015, 28(1): 102. WANG Xiang, CHEN Xiaohong, YANG Xiangmei. Short term prediction of expressway travel time based on k nearest neighbor algorithm[J]. China Journal of Highway and Transport, 2015, 28(1): 102. DOI:10.3969/j.issn.1001-7372.2015.01.014 |
| [17] |
于明, 皮海龙, 王岩, 等. 基于k近邻法和脊线追踪的指纹匹配算法[J]. 吉林大学学报(工学版), 2014, 44(6): 1806. YU Ming, PI Hailong, WANG Yan, et al. Fingerprint matching algorithm based on k-nearest neighbor and ridge line tracking methods[J]. Journal of Jilin University (Engineering andTechnology Edition), 2014, 44(6): 1806. |
| [18] |
马娟, 朵云峰, 赵文亮. 两种空间分块策略k近邻搜索算法的比较研究[J]. 中国图象图形学报, 2011, 16(9): 1676. MA Juan, DUO Yunfeng, ZHAO Wenliang. Comparison of two algorithms for finding k-nearest neighbors based on spatial sub-cubes[J]. Journal of Image and Graphics, 2011, 16(9): 1676. |
| [19] |
叶涛, 朱学峰, 李向阳, 等. 基于改进k-最近邻回归算法的软测量建模[J]. 自动化学报, 2007, 33(9): 996. YE Tao, ZHU Xuefeng, LI Xiangyang, et al. Soft sensor modeling based on a modified k-nearest neighbor regression algorithm[J]. Acta Automatica Sinica, 2007, 33(9): 996. |
| [20] |
陈婧敏. 基于KNN回归的短时交通流预测[J]. 微型电脑应用, 2015, 31(9): 25. CHEN Jingmin. Short-term traffic flow forecast based on knn regression[J]. Microcomputer Applications, 2015, 31(9): 25. DOI:10.3969/j.issn.1007-757X.2015.09.008 |
 2018, Vol. 50
2018, Vol. 50


