2. 中国石油大学(华东) 化学工程学院,山东 青岛 266555
2. College of Chemical Engineering, China University of Petroleum, Qingdao 266555, Shandong, China
近年来沥青与集料的交互作用、集料的表面能理论在道路工程中受到越来越多研究者的关注,文献[1-2]研究指出:沥青-集料的交互作用能力是影响沥青混合料路用性能的重要因素、不同沥青与石粉产生的交互作用能力有所不同.文献[3]研究了温拌沥青表面能及温拌沥青与石灰岩、花岗岩的黏附功;文献[4-5]基于表面能理论研究了温拌沥青混合料劈裂强度及水稳性能;文献[6-9]对矿粉表面能试验方法、表面能理论在湖沥青中灰分的改性机能理论研究了矿粉的粒径对沥青胶浆高温性能的影响.文献[10]从表面能理论的角度研究了沥青混合料的抗剥落性能,文献[11-13]从表面能的角度研究了沥青-集料的黏附性,文献[14-15]等从矿粉表面能的角度研究了矿粉粒径对沥青胶浆性能的影响及湖沥青的改性机理.面对应用越来越广泛的集料(矿粉)表面能,前期研究发现,在变化不定的集料(矿粉)中,存在不变化的因素,即其主要化学成分相同,主要为氧化钙、氧化镁、氧化铁、氧化硅、氧化铝等5种氧化物(约占其所有氧化物质量的95%~99%).基于此,本文针对变化的矿粉与不变化的化学成分展开表面能试验研究,探究其内在规律,建立量化模型,为其在道路工程中更深入的应用提供理论指导.
1 研究方案与试验结果 1.1 试验方法与试验材料矿粉、矿粉主要化学成分的表面能试验方法采用毛细管上升法[6]测得其与表面能已知的液体的接触角,然后计算得到.
矿粉为4种不同料源的石灰岩矿粉(记为S1、S2、S3、S4)以及一种玄武岩矿粉(记为X),通过XRD法测得其化学成分的质量分数见图 1.
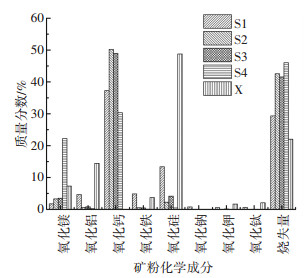
|
图 1 矿粉化学成分质量分数 Figure 1 Chemical composition contents of mineral filler |
由图 1可以看出,前5种化学成分占所有化学成分的质量分数在95%以上,可见,选择前5种化学成分作为矿粉所含化学成分的代表是合理的.
根据前期研究及文献[14-15]可知,矿粉的粒径大小对其表面能有显著影响,基于此,为了排除矿粉粒径大小不统一而对试验结果产生不利的影响,文章对上述5种矿粉进行了进一步分档处理:200目(0.074~0.15 mm)、300目(0.053~0.075 mm)、400目(0.038 5~0.053 mm)、500目(0.030 8~0.038 5 mm).
本文采用的矿粉的5种化学成分均是从阿拉丁网站购买,均具备产品检验证书,试剂的主要指标(厂家出厂指标)见表 1.
| 表 1 5种化学成分指标 Table 1 Indexes of five chemical compositions |
本文测表面能所用试剂从阿拉丁网站购买试剂主要指标见表 2.
| 表 2 4种液体试剂指标 Table 2 Indexes of four liquid reagents |
通过1.1节方法测定5种矿粉和5种化学成分的表面能,结果见图 2、3.
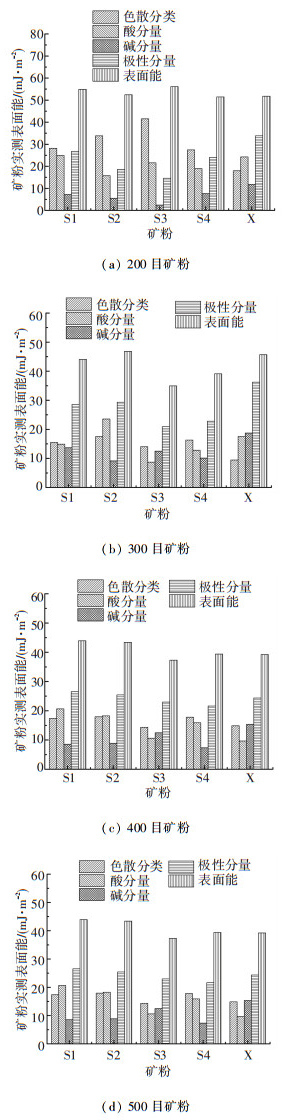
|
图 2 5种矿粉实测表面能 Figure 2 Surface energy of five mineral fillers |
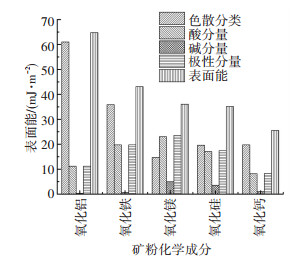
|
图 3 5种化学成分表面能 Figure 3 Surface energy of five chemical compositions |
本节主要采用灰色理论中的灰色关联度对试剂表面能、矿粉的化学成分质量分数、矿粉的表面能之间的关系进行分析,以研究矿粉的表面能与其化学成分之间的关系.本文所采用的5种矿粉所含化学成分如图 1所示.
假设矿粉的表面能W与其化学成分的表面能ωi参数之间存在随着化学成分质量分数θi变化的关系为
| $ {W_c} = \sum\limits_{i = 1}^5 {{\omega _i} \times {\theta _i}} . $ | (1) |
式中:Wc为矿粉表面能计算值(色散分量、酸分量、碱分量、极性分量、表面能),mJ·m-2;ωi为矿粉的第i种化学成分的、与W对应的表面能,mJ·m-2;θi为矿粉第i种化学成分质量分数.
则可根据图 1中化学成分质量分数、图 3中化学成分的表面能、式(1)计算得出5种矿粉的表面能的计算值Wc,计算结果见图 4.

|
图 4 5种矿粉表面能计算值(Wc) Figure 4 Calculated surface energy of five mineral fillers (Wc) |
将图 4中矿粉表面能计算值与图 2中不同粒径的矿粉表面能实测值进行灰色关联,灰色关联度见图 5.

|
图 5 矿粉表面能计算值与实测值关联度 Figure 5 Correlation between calculated and measured surface energy |
图 5表明矿粉的表面能实测值,与通过其化学成分表面能计算的计算值之间,表面能的实测值与计算值对200~500目矿粉而言,均存在较高的关联度;对色散分量而言,除300目矿粉的实测结果与计算结果关联度相对较小之外,其他粒径的矿粉的表面能色散分量的实测值与计算值之间,均存在较好的关联度.
2.2 矿粉所含化学成分表面能与矿粉表面能间关系模型1) 研究依据.由2.1节的分析可知,矿粉的表面能与其所含化学成分的表面能理论值之间存在良好的灰色关联度,基于此,该部分将围绕上述指标之间的具体关系模型的探索展开.
2) 数据处理.本文采用的5种矿粉的化学成分组成见图 1,各化学成分表面能见图 3,5种矿粉实测表面能见图 2.该部分通过数据统计软件进行分析.为了进行矿粉所含化学成分表面能与矿粉表面能之间关系的寻求,首先对化学成分质量分数、化学成分表面能进行处理.
将某一种矿粉的化学成分质量分数乘以对应化学成分的表面能(以下简称复合表面能),即将图 1中的数值乘以图 3中对应的数值,可得到行数、列数相等的一个新的矩阵,详见表 3.
| 表 3 复合表面能 Table 3 Compound surface energy |
为了确定表 3中各化学成分复合表面能与矿粉表面能之间的关系,需先对不同化学成分的复合表面能之间的相关性进行分析,若相关性较高,则需进行主成份分析.采用SPSS 22.0中的“因子分析”可得出5种材料的各化学成分复合表面能之间的相关性系数,详见表 4~8.
| 表 4 S1所含化学成分复合表面能相关性 Table 4 Correlation of compound surface energy of the chemical compositions in S1 |
| 表 5 S2所含化学成分复合表面能相关性 Table 5 Correlation of compound surface energy of the chemical compositions in S2 |
| 表 6 S3所含化学成分复合表面能相关性 Table 6 Correlation of compound surface energy of the chemical compositions in S3 |
| 表 7 S4所含化学成分复合表面能相关性 Table 7 Correlation of compound surface energy of the chemical compositions in S4 |
| 表 8 X所含化学成分复合表面能相关性汇总表 Table 8 Correlation of compound surface energy of the chemical compositions in X |
由表 4~8可以看出,不同化学成分的复合表面能间相关系数,除氧化镁与氧化铁、氧化硅、氧化钙之间相对较低之外,其他相互之间相关系数均较大.基于此,为了在进行回归分析中,能将所有的变量都考虑进模型,需对各自变量先进行主成份分析.采用SPSS 22.0中的“降维”的“因子分析”的“主成份分析”,对表 4~8中5种化学成分复合表面能进行主成份分析,经该处理,上述5个表中的5个变量被处理为一个主成分因子,结果见表 9.
| 表 9 矿粉各化学成分复合表面能主成份分析得分结果 Table 9 Main component analysis scores of compound surface energy of mineral fillers |
由表 9中的主成份因子分别乘以表 3中的5个自变量并相加,即可得到5种矿粉所含化学成分的复合表面能的主成份变量见表 10.
| 表 10 矿粉所含化学成分的复合表面能的主成份变量 Table 10 Main component variables of compound surface energy of mineral fillers |
本文分别对200、300、400、500目矿粉的表面能进行了试验,在该4个粒径的矿粉的表面能中,如何确定可以代表矿粉表面能的值,以用于评价其与所含化学成分表面能的关系.可见,需通过实测的4个粒径的矿粉的表面能实测值,采用统计的手段,统计出可代表矿粉本身表面能的变量.通过SPSS 22.0的因子分析,可由4个粒径的矿粉的表面能计算得到代表各矿粉表面能的主成份变量,详见表 11.
| 表 11 5种矿粉表面能主成份变量结果 Table 11 Main component variables of surface energy of five mineral fillers |
以表 10中矿粉所含化学成分复合表面能为自变量,以表 11中矿粉表面能主成份变量为因变量,建立矿粉表面能与所含化学成分表面能的关系模型,上述模型的建立,采用SPSS 22.0中的“回归→线性”,结果见表 12.
| 表 12 矿粉表面能与其化学成分表面能线性回归模型 Table 12 Regression models of surface energy of mineral fillers and its chemical compositions |
表 12中分别采用了回归方差经过原点、不经过原点两种方式,由表中可见,对本文而言,采用经过原点的方式,回归方程的相关系数显著高于不经过原点的回归方程.由表 12计算可得4种石灰岩的矿粉表面能与所含化学成分的复合表面能的回归方程的斜率的均值分别为8.63(不经过原点回归)、11.76(经过原点回归),玄武岩的斜率分别为2.88(不经过原点回归)、5.04(经过原点回归).基于以上分析,可以得出矿粉表面能与其化学成分质量分数及其对应表面能之间的关系模型如下.
2.3 模型提出1) 自变量矩阵的确定.令矿粉的5种化学成分质量分数矩阵为
| $ \mathit{\boldsymbol{C}} = \left\{ {{c_{{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}}, {c_{{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}, {c_{{\rm{MgO}}}}, {c_{{\rm{Si}}{{\rm{O}}_2}}}, {c_{{\rm{CaC}}{{\rm{O}}_3}}}} \right\}. $ | (2) |
5种化学成分的表面能矩阵为
| $ \mathit{\boldsymbol{\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\gamma _{{\rm{d}} - {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{d}} - {\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{d}} - {\rm{MgO}}}}}&{{\gamma _{{\rm{d}} - {\rm{Si}}{{\rm{O}}_2}}}}&{{\gamma _{{\rm{d}} - {\rm{CaC}}{{\rm{O}}_3}}}}\\ {{\gamma _{{\rm{a}} - {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{a}} - {\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{a}} - {\rm{MgO}}}}}&{{\gamma _{{\rm{a}} - {\rm{Si}}{{\rm{O}}_2}}}}&{{\gamma _{{\rm{a}} - {\rm{CaC}}{{\rm{O}}_3}}}}\\ {{\gamma _{{\rm{b}} - {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{b}} - {\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{b}} - {\rm{MgO}}}}}&{{\gamma _{{\rm{b}} - {\rm{Si}}{{\rm{O}}_2}}}}&{{\gamma _{{\rm{b}} - {\rm{CaC}}{{\rm{O}}_3}}}}\\ {{\gamma _{{\rm{p}} - {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{p}} - {\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{p}} - {\rm{MgO}}}}}&{{\gamma _{{\rm{p}} - {\rm{Si}}{{\rm{O}}_2}}}}&{{\gamma _{{\rm{p}} - {\rm{CaC}}{{\rm{O}}_3}}}}\\ {{\gamma _{{\rm{s}} - {\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{s}} - {\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}}}&{{\gamma _{{\rm{s}} - {\rm{MgO}}}}}&{{\gamma _{{\rm{s}} - {\rm{Si}}{{\rm{O}}_2}}}}&{{\gamma _{{\rm{s}} - {\rm{CaC}}{{\rm{O}}_3}}}} \end{array}} \right]. $ | (3) |
式(3)中,下标s、d、a、p、b分别表示5种化学成分表面能(surface energy)、色散分量(dispersion component)、酸分量(acid component)、极性分量(polarity component)、碱分量(base component).矿粉所含化学成分复合表面能矩阵为
| $ {\mathit{\boldsymbol{\gamma }}^ * } = \mathit{\boldsymbol{\gamma }} \times \mathit{\boldsymbol{C}}. $ | (4) |
通过SPSS软件对γ*矩阵进行主成份分析,得主成份因子矩阵为
| $ \mathit{\boldsymbol{F}} = \left(\begin{array}{l} {F_{1{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}} \cdots {F_{{\rm{nA}}{{\rm{l}}_2}{{\rm{O}}_3}}}\\ {F_{1{\rm{F}}{{\rm{e}}_2}{{\rm{O}}_3}}} \cdots {F_{{\rm{nF}}{{\rm{e}}_2}{{\rm{O}}_3}}}\\ {F_{1{\rm{MgO}}}} \cdots {F_{{\rm{nMgO}}}}\\ {F_{1{\rm{Si}}{{\rm{O}}_2}}} \cdots {F_{{\rm{nSi}}{{\rm{O}}_2}}}\\ {F_{1{\rm{CaC}}{{\rm{O}}_3}}} \cdots {F_{{\rm{nCaC}}{{\rm{O}}_3}}} \end{array} \right). $ | (5) |
矩阵γ*与矩阵F相乘可计算得到矿粉化学成分主成分变量矩阵(自变量F*)为
| $ {\mathit{\boldsymbol{F}}^ * } = {\mathit{\boldsymbol{\gamma }}^ * } \times \mathit{\boldsymbol{F}} = \left( {\mathit{\boldsymbol{F}}_{m1}^ * , \cdots , \mathit{\boldsymbol{F}}_{mn}^ * } \right). $ | (6) |
Fm*矩阵为一个5行、n列的矩阵,每一列表示经主成分分析后的一个抽象化的氧化物复合表面能,m为1~5,分别表示5种化学成分.其中(Fmi*)模型为
| $ (\mathit{\boldsymbol{F}}_{mi}^ * ) = {\mathit{\boldsymbol{\gamma }}^ * } \times \mathit{\boldsymbol{F}}. $ | (7) |
2) 因变量.同一矿粉、4个粒径的表面能试验结果矩阵为
| $ {\mathit{\boldsymbol{\gamma }}_m} = \left( {\begin{array}{*{20}{c}} {{\gamma _{{\rm{d}} - 200}}}&{{\gamma _{{\rm{d}} - 300}}}&{{\gamma _{{\rm{d}} - 400}}}&{{\gamma _{{\rm{d}} - 500}}}\\ {{\gamma _{{\rm{a}} - 200}}}&{{\gamma _{{\rm{a}} - 300}}}&{{\gamma _{{\rm{a}} - 400}}}&{{\gamma _{{\rm{a}} - 500}}}\\ {{\gamma _{{\rm{b}} - 200}}}&{{\gamma _{{\rm{b}} - 300}}}&{{\gamma _{{\rm{b}} - 400}}}&{{\gamma _{{\rm{b}} - 500}}}\\ {{\gamma _{{\rm{p}} - 200}}}&{{\gamma _{{\rm{p}} - 300}}}&{{\gamma _{{\rm{p}} - 400}}}&{{\gamma _{{\rm{p}} - 500}}}\\ {{\gamma _{{\rm{s}} - 200}}}&{{\gamma _{{\rm{s}} - 300}}}&{{\gamma _{{\rm{s}} - 400}}}&{{\gamma _{{\rm{s}} - 500}}} \end{array}} \right). $ | (8) |
通过SPSS软件对γm矩阵进行主成份分析,得主成份因子矩阵为
| $ {\mathit{\boldsymbol{F}}_{\rm{m}}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{200}}}\\ {{\mathit{\boldsymbol{F}}_{300}}}\\ {{\mathit{\boldsymbol{F}}_{400}}}\\ {{\mathit{\boldsymbol{F}}_{500}}} \end{array}} \right). $ | (9) |
矩阵γm与矩阵F相乘可计算得到矿粉化学成分主成分变量矩阵(因变量Fm*)为
| $ \mathit{\boldsymbol{F}}_m^ * = {\mathit{\boldsymbol{\gamma }}_m} \times {\mathit{\boldsymbol{F}}_{\rm{m}}} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}}_d^ * }\\ {\mathit{\boldsymbol{F}}_a^ * }\\ {\mathit{\boldsymbol{F}}_b^ * }\\ {\mathit{\boldsymbol{F}}_p^ * }\\ {\mathit{\boldsymbol{F}}_s^ * } \end{array}} \right). $ | (10) |
3) 矿粉化学成分质量分数及其表面能与矿粉表面能关系模型由自变量矩阵F*、因自变量矩阵Fm*,通过相关统计软件进行两者关系模型的求解.
3 结论1) 矿粉的表面能实测值,与通过其化学成分表面能计算的计算值之间基本均存在较好的关联度,可见,矿粉的化学成分的表面能及其化学成分质量分数对矿粉的表面能有着决定性的影响.
2) 建立了变化的矿粉表面能、变化的化学成分质量分数与不变的化学成分表面能之间的定量关系模型,其中石灰岩、玄武岩矿粉模型参数的显著差异及较高的相关系数证明了模型的可靠性.
3) 通过提出的模型,可对不同岩石加工的矿粉,在测得其化学成分质量分数后,直接计算得到矿粉的表面能,可为矿粉表面能在道路工程中的应用的深入研究提供理论指导.
| [1] |
谭忆秋, 李晓琳, 周兴业, 等. 花岗岩矿料与沥青交互作用能力的研究[J]. 哈尔滨工业大学学报, 2009, 41(11): 95. TAN Yiqiu, LI Xiaolin, ZHOU Xingye, et al. Interaction capability of granite aggregate and asphalt[J]. Journal of Harbin Institute of Technology, 2009, 41(11): 95. DOI:10.3321/j.issn:0367-6234.2009.11.020 |
| [2] |
谭忆秋, 吴建涛, 李晓民, 等. 沥青与集料交互作用能力的评价指标[J]. 哈尔滨工业大学学报, 2009, 41(7): 81. TAN Yiqiu, WU Jiantao, LI Xiaoming, et al. Evaluation indexes for interaction capability of asphalt and aggregate[J]. Journal of Harbin Institute of Technology, 2009, 41(7): 81. DOI:10.3321/j.issn:0367-6234.2009.07.018 |
| [3] |
郭鹏, 唐伯明, 冯敏, 等. 基于表面自由能理论的温拌再生沥青-集料粘附特性[J]. 长安大学学报(自然科学版), 2014, 34(4): 38. GUO Peng, TANG Boming, FENG Min, et al. Warm mix recycled asphalt-aggregates adhesion based on surface free energy theory[J]. Journal of Chang'an University (Natural Sciences), 2014, 34(4): 38. DOI:10.3969/j.issn.1671-8879.2014.04.007 |
| [4] |
成志强, 孔繁盛. 矿料表面能对沥青混合料劈裂强度的影响[J]. 建筑材料学报, 2016, 19(4): 779. CHENG Zhiqiang, KONG Fansheng. Effect of aggregate surface energy parameters on splitting strength of asphalt mixture[J]. Journal of Building Materials, 2016, 19(4): 779. DOI:10.3969/j.issn.1007-9629.2016.04.030 |
| [5] |
成志强.基于界面特性的温拌再生沥青混合料水稳性能研究[D].重庆: 重庆交通大学, 2013 CHENG Zhiqiang. Moisture sensitivity of warm mix recycled asphalt mixture based on theory ofinterface[D]. Chongqing: Chongqing Jiaotong University, 2013 |
| [6] |
孔令云, 曹慧平. 影响毛细管上升法测矿粉接触角的外因及解决方法[J]. 哈尔滨工业大学学报, 2017, 49(9): 121. KONG Lingyun, CAO Huiping. External factors for contact angle of mineral filler with capillary rise method and solution method[J]. Journal of Harbin Institute of Technology, 2017, 49(9): 121. |
| [7] |
孔令云, 代笠, 莫石秀, 等. 基于粘附理论的TLA中灰分填料改性作用定量分析[J]. 重庆交通大学学报(自然科学版), 2017, 36(6): 54. KONG Lingyun, DAI Li, MO Shixiu, et al. Quantitative analysis of modification effect of ash filler in TLA based on adhesion theory[J]. Journal of Chongqing Jiaotong University (Natural Science), 2017, 36(6): 54. |
| [8] |
孔令云, 徐燕, 成志强. 基于表面能的Sasobit©影响WMA劈裂强度机理研究[J]. 建筑材料学报, 2015, 18(4): 669. KONG Lingyun, XU Yan, CHENG Zhiqiang. Study on the mechanism of WMA splitting strength of sasobit base on surface free energy[J]. Journal of Building Materials, 2015, 18(4): 669. DOI:10.3969/j.issn.1007-9629.2015.04.023 |
| [9] |
KONG Lingyun, MO Shixiu. High-temperature performance of asphalt mortar using surface and interface theory[J]. Journal of Materials in Civil Engineering, 2015, 27(8): C4014009. DOI:10.1061/(ASCE)MT.1943-5533.0001185 |
| [10] |
孙瑜, 李立寒. 基于表面能理论的沥青混合料抗剥落性能[J]. 建筑材料学报, 2016, 19(4): 286. SUN Yu, LI Lihan. Anti-stripping of asphalt mixture based on surface energy theory[J]. Journal of Building Materials, 2016, 19(4): 286. |
| [11] |
陈燕娟, 高建明, 陈华鑫. 基于表面能理论的沥青-集料体系的黏附特性研究[J]. 东南大学学报(自然科学版), 2014, 44(1): 184. CHEN Yanjuan, GAO Jianming, CHEN Huaxin. Research on adhesion in asphalt-aggregate systems based on surface energy theory[J]. Journal ofSoutheast University (Natural Sciences), 2014, 44(1): 184. |
| [12] |
裴建新. 基于表面能法的沥青-集料粘附机理研究[J]. 合成材料老化与应用, 2016, 17(4): 74. PEI Jianxin. Adhesionmechanism of asphalt add aggregate by surface energy method[J]. Synthetic Materials Aging and Application, 2016, 17(4): 74. DOI:10.3969/j.issn.1671-5381.2016.04.017 |
| [13] |
易军艳, 曹一翔, 王东升, 等. 钨酸锆填料与沥青的粘附与水损害特性[J]. 哈尔滨工业大学学报, 2017, 49(3): 127. YI Junyan, CAO Yixiang, WANG Dongsheng, et al. Adhesive bond and moisture damage mechanism of asphalt mastic made with zirconium tungstate[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 127. |
| [14] |
莫石秀, 孔令云, 王娜. 矿粉粒径对沥青胶浆性能影响试验研究[J]. 广西大学学报(自然科学版), 2011, 38(4): 616. MO Shixiu, KONG Lingyun, WANG Na. Study of influence of mineral filler diameter on asphalt mortar[J]. Journal of Guangxi University (Natural Sciences), 2011, 38(4): 616. DOI:10.3969/j.issn.1001-7445.2011.04.016 |
| [15] |
莫石秀.湖沥青改性沥青作用机理及混合料性能研究[D].西安: 长安大学, 2012 MO Shixiu. Study on trinidad lake asphalt modified asphalt action mechanism and mixture performance[D]. Xi'an: Chang'an University, 2012 |
 2018, Vol. 50
2018, Vol. 50


