在不同行驶工况及需求功率条件下,混合动力车辆(Hybrid Electric Vehicle,HEV)的动力源有不同的工作组合方式[1].由于发动机和电机的动态特性存在明显差异[2],导致动力源在合成转矩时,容易对车辆动力传动系统产生较大冲击,影响车辆的动力性和驾乘人员的舒适性[3].
近年来国内外学者对模式切换过程中的动态协调控制投入了大量研究.丰田PRIUS以行星齿轮机构作为动力耦合装置,在驱动模式切换时利用电动机响应迅速对发动机转矩进行补偿[4-5],使模式切换平滑.温博轩等[6]提出多动力源协调控制策略,减小动态响应过程的波动. Hwang等[7]针对行星式混合动力系统的发动机启停过程进行分析,证明采用一种阻尼旁通离合器能够有效降低启停过程的转矩波动.而当发动机与减振器共振时,硬件无法起到减振的作用,Tomura等[8]基于此提出利用电机MG1补偿发动机启动过程中脉动扭矩,利用电机MG2实现系统的扭振控制,并通过试验验证了该策略的主动减振效果. Zhu等[9-10]针对一种多模行星式混合动力系统的发动机启动过程,采用模糊增益调节PID进行动态协调,有效降低了系统冲击度和离合器滑磨功. Syed等[11]针对行星式混合动力系统设计了车轮扭矩的主动减振控制系统,在无需额外传感器的前提下,利用电机进行主动减振前馈控制,有效抑制了系统输出扭矩的波动.对于行星式混合动力系统在发动机启动阶段,主要期望是获得良好的系统平顺性.
以上研究对象多为乘用车,由于发动机类型的不同,与本文研究对象——行星式混合动力客车所采用的柴油机具有不同的动态特性[12],因此动态协调问题也有所差异.考虑引起系统冲击的主要原因是当前控制变量与系统未来状态之间的不协调,本文将行星式混合动力客车系统的发动机启动过程视作受约束的多目标优化问题.与其他控制方法相比,MPC可以同时利用过去、当前和预测得到的未来的偏差值,在线滚动优化获得最优控制序列,使得未来一段时间内被控变量与期望值偏差最小.于是本文提出一种基于数据驱动的MPC控制器,实现发动机的启动控制.并基于Matlab/Simulink搭建系统仿真模型,对MPC控制器在模式切换过程中抑制冲击度的效果进行验证.
1 系统构型本文的研究对象为具有行星式混合动力系统的城市客车,系统构型如图 1所示.该系统具有3个动力源,发动机、电机MG1和电机MG2,包括两排行星齿轮机构PG1和PG2.前行星排PG1为系统的功率分流机构,后行星排PG2的齿圈固定连接在机壳上,其功能等效为固定速比减速器.发动机输出轴连接前行星排的行星架,电机MG1连接PG1的太阳轮,电机MG2连接PG2的太阳轮,PG1的齿圈与PG2的行星架相连,并将整个系统的动力输出到主减速器.该构型可实现纯电动(EV)模式、混合动力(EVT)模式和再生制动(RGB)等多种驱动模式.

|
图 1 系统结构简图 Figure 1 Configuration of system |
为建立该系统的动力学模型,将该系统分为前行星排PG1、后行星排PG2和系统输出三部分,分别建立自由体图,进行动力学研究.
忽略行星齿轮机构内部各构件间的摩擦损失,得到前行星排PG1和后行星排PG2中行星轮、太阳轮和齿圈之间的转速、转矩关系分别为
| $ \left\{ \begin{array}{l} {T_{{\rm{s1}}}} = {T_{{\rm{c1}}}}/\left( {1 + {k_1}} \right),\\ \left( {1 + {k_1}} \right){\omega _{{\rm{c1}}}} = {k_1}{\omega _{{\rm{rl}}}} + {\omega _{{\rm{sl}}}}. \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} {T_{{\rm{s2}}}} = {T_{{\rm{c2}}}}/\left( {1 + {k_2}} \right),\\ \left( {1 + {k_2}} \right){\omega _{{\rm{c2}}}} = {\omega _{{\rm{s2}}}}. \end{array} \right. $ | (2) |
式中:T和ω分别表示转矩和转速,下标c1、s1和r1分别表示前行星排PG1的行星架、太阳轮和齿圈,k1、k2表示前后行星排的特征参数,下标c2和s2分别表示后行星排PG2的行星架和太阳轮.
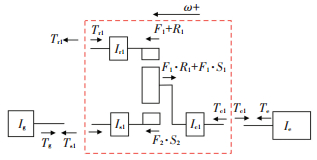
图 2为前行星排PG1的自由体图,表征发动机在电机MG1的作用下,通过前行星排齿圈输出转矩.虚线框内所示部分为前行星PG1的齿轮机构.将行星轮视作理想的传力机构,在忽略摩擦损失和粘滞损失的情况下,得到前行星排PG1的基本动力学关系为
| $ {I_{{\rm{r1}}}}{{\dot \omega }_{{\rm{r1}}}} = {F_1} \cdot {R_1} - {T_{{\rm{r1}}}}, $ | (3) |
| $ {I_{{\rm{c1}}}}{{\dot \omega }_{{\rm{c1}}}} = {T_{{\rm{c1}}}} - {F_1} \cdot {S_1} - {F_1} \cdot {R_1}, $ | (4) |
| $ {I_{{\rm{s1}}}}{{\dot \omega }_{{\rm{s1}}}} = {F_1} \cdot {S_1} - {T_{{\rm{s1}}}}. $ | (5) |
|
图 2 前行星排自由体图 Figure 2 Free-body diagram of front planetary gear set |
式中:I表示转动惯量,R1和S1为前排齿圈和太阳轮的半径,F1表示前排行星轮的内力.
规定向左的转矩和转速为正方向,结合前行星排PG1内部转矩关系与式(4)、式(5)可以得到
| $ \left( {{I_{\rm{e}}} + {I_{{\rm{c1}}}}} \right){{\dot \omega }_{\rm{e}}} = {T_{\rm{e}}} - {F_1} \cdot {R_1} - {F_1} \cdot {S_1}, $ | (6) |
| $ \left( {{I_{\rm{g}}} + {I_{{\rm{s1}}}}} \right){{\dot \omega }_{\rm{g}}} = {F_1} \cdot {S_1} - {T_{\rm{g}}}. $ | (7) |
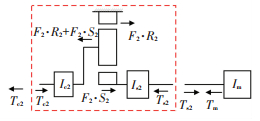
图 3为后行星排PG2的自由体图,表征MG2经过后行星排的齿轮机构(虚线框内所示部分)的减速增扭作用后,并最终从后齿圈输出转矩.
|
图 3 后行星排自由体图 Figure 3 Free-body diagram of rear planetary gear set |
分析同前,结合后行星排转速关系,后行星排PG2输出转矩Tc2与输入转矩Tm之间的关系为
| $ {T_{{\rm{c2}}}} = {T_{\rm{m}}}\left( {1 + {k_2}} \right) - \left[ {\left( {{I_{\rm{m}}} + {I_{{\rm{s2}}}}} \right){{\left( {1 + {k_2}} \right)}^2} - {I_{{\rm{c2}}}}} \right]{{\dot \omega }_{{\rm{c2}}}}. $ | (8) |
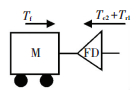
图 4为输出部分的自由体图,表征前行星排齿圈和后行星排行星架的输出转矩耦合后传递给主减速器FD,用于克服车辆的行驶阻力.
|
图 4 输出部分自由体图 Figure 4 Free body diagram of system output |
在仅考虑车辆纵向动力学,并忽略车轮打滑的前提下,结合式(3)和式(8)得到
| $ \begin{array}{l} {{\dot \omega }_{{\rm{r1}}}}\left[ {\frac{{{R_{\rm{t}}}^2m}}{{{i_{\rm{o}}}}} + {I_{{\rm{r1}}}}{i_{\rm{o}}} + \left( {{I_{\rm{m}}} + {I_{{\rm{s2}}}}} \right)\left( {1 + {k_2}} \right)2{i_{\rm{o}}} - {I_{{\rm{c2}}}}{i_{\rm{o}}}} \right] = \\ \;\;\;\left[ {{T_{\rm{m}}}\left( {1 + {k_2}} \right) + {F_1}{R_1}} \right]{i_{\rm{o}}} - {T_{\rm{f}}}. \end{array} $ | (9) |
式中Tf为车辆受到的阻力矩.在平直路行驶时,Tf的计算公式为
| $ {T_{\rm{f}}} = {T_{{\rm{fb}}}} + mg{f_{\rm{r}}}{R_{\rm{t}}} + 0.5\rho A{C_{\rm{D}}}{\left( {{\omega _{{\rm{r1}}}}/{i_{\rm{o}}}} \right)^2}{R_{\rm{t}}}^3. $ |
式中: Tfb为制动力矩,fr为滚动阻力系数,ρ为空气密度,A为迎风面积,CD为车辆的空气阻力系数,i0为主减速器传动比,Rt为车轮半径.
至此,由前后行星排的转速转矩关系式(1)和式(2),并结合式(6)、(7)、(9),便可以描述本文研究对象的动力传动情况.
2.2 车辆运行过程动态方程推导依据前行星排PG1的动力学关系,用发动机转速和齿圈转速表示电机MG1转速,由式(6)、(7)可得
| $ {{I'}_{\rm{g}}}{k_1}{{\dot \omega }_{{\rm{r1}}}} - \left[ {\frac{{{{I'}_{\rm{e}}}}}{{1 + {k_1}}} + {{I'}_{\rm{g}}}\left( {1 + {k_1}} \right)} \right]{{\dot \omega }_{\rm{e}}} = {T_{\rm{g}}} - \frac{{{T_{\rm{e}}}}}{{1 + {k_1}}}, $ | (10) |
式中Ie′=Ie+Ic1,Ig′=Is1+Ig.
由于发动机在怠速之前输出的转矩具有非线性、时变性等特点[13],难以获得精确的发动机怠速数学模型,本文基于大量有关实车的历史数据对发动机工作各区间的转速、转矩及转矩变化率进行统计分析,对发动机怠速之前输出转矩进行线性化处理.以其中一段为例介绍线性化处理过程,图 5为发动机启动阶段的工作点分布,当发动机上升至440 r/min附近时,开始喷油输出转矩,转矩快速上升,达到290 Nm附近后,又开始随发动机转速的上升平稳下降,该区间的发动机转矩可以近似模拟为基于转速的分段线性函数,利用最小二乘法进行数据拟合.

|
图 5 发动机工作点 Figure 5 Engine operation point |
构造分段函数描述发动机怠速前转速与转矩间的关系,令Te=αωe+β,式中α和β为基于转速的分段常数.
| $ \left\{ \begin{array}{l} \alpha = {\alpha _1},\beta = {\beta _1},{\omega _{\rm{e}}} < 440\;{\rm{r/min}};\\ \alpha = {\alpha _2},\beta = {\beta _2},440\;{\rm{r/min}} \le {\omega _{\rm{e}}} < 460\;{\rm{r/min;}}\\ \alpha = {\alpha _3},\beta = {\beta _3},460\;{\rm{r/min}} \le {\omega _{\rm{e}}} < 567\;{\rm{r/min;}}\\ \alpha = {\alpha _4},\beta = {\beta _4},567\;{\rm{r/min}} \le {\omega _{\rm{e}}} < 640\;{\rm{r/min;}}\\ \alpha = {\alpha _5},\beta = {\beta _5},{\omega _{\rm{e}}} \ge 640\;{\rm{r/min}}. \end{array} \right. $ |
结合后行星排PG2和输出部分的关系得到
| $ \begin{array}{*{20}{c}} {\left[ {\frac{{R_{\rm{t}}^2m}}{{{i_0}}} + {I_{\rm{m}}}{{\left( {1 + {k_2}} \right)}^2}{i_0}} \right]{{\dot \omega }_{r1}} + {I_{\rm{e}}}\frac{{{k_1}}}{{1 + {k_1}}}{i_0}{{\dot \omega }_{\rm{e}}} = }\\ {{T_{\rm{m}}}\left( {1 + {k_2}} \right){i_0} + \frac{{\alpha {\omega _e}{k_1}}}{{1 + {k_1}}}{i_0} + \frac{{\beta {k_1}}}{{1 + {k_1}}}{i_0} - {T_{\rm{f}}}.} \end{array} $ | (11) |
根据车辆行驶过程的系统动态方程及实际控制需求,定义发动机转速ωe和前行星排齿圈转速ωr1为状态变量,MG1输出扭矩Tg和MG2输出扭矩Tm为输入变量,将发动机转速ωe作为输出量.联立式(10)和式(11),系统的状态空间表达式可以化为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = {\mathit{\boldsymbol{A}}_{\rm{c}}}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_{{\rm{cu}}}}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{B}}_{{\rm{cd}}}}\mathit{\boldsymbol{d}},\\ y = \mathit{\boldsymbol{Cx}}. \end{array} \right. $ |
式中:x =[ωe ωr1]T,u =[Tg Tm]T,
| $ \mathit{\boldsymbol{d}} = {\left[ {\begin{array}{*{20}{c}} { - \frac{\beta }{{1 + {k_1}}}}&{\frac{{\beta {k_1}}}{{1 + {k_1}}}{i_{\rm{o}}} - {T_{\rm{f}}}} \end{array}} \right]^{\rm{T}}},y = {\omega _{\rm{e}}}, $ |
| $ {\mathit{\boldsymbol{A}}_{\rm{o}}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{{{I'}_{\rm{e}}}}}{{1 + {k_1}}} - {{I'}_{\rm{g}}}\left( {1 + {k_1}} \right)}&{{{I'}_{\rm{g}}}{k_1}}\\ {{I_{\rm{e}}}\frac{{{k_1}}}{{1 + {k_1}}}{i_{\rm{o}}}}&{\frac{{R_{\rm{t}}^2m}}{{{i_{\rm{o}}}}} + {I_{\rm{m}}}{{\left( {1 + {k_2}} \right)}^2}{i_{\rm{o}}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{A}}_{\rm{c}}} = {\mathit{\boldsymbol{A}}_{\rm{o}}}^{ - 1}\left[ {\begin{array}{*{20}{c}} { - \frac{\alpha }{{1 + {k_1}}}}&0\\ {\frac{{\alpha {k_1}}}{{1 + {k_1}}}{i_o}}&0 \end{array}} \right],{\mathit{\boldsymbol{B}}_{{\rm{cu}}}} = {\mathit{\boldsymbol{A}}_{\rm{o}}}^{ - 1}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{\left( {1 + {k_2}} \right){i_{\rm{o}}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{B}}_{{\rm{cd}}}} = {\mathit{\boldsymbol{A}}_{\rm{o}}}^{ - 1},\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]. $ |
根据模型预测控制的基本原理[14],应用模型预测被控系统的未来动态,通过求解目标优化问题,获得优化控制量序列,将最优解的第一个值作用于系统,在下一时刻,重新获取系统采样信息并刷新优化问题,再次求解目标优化问题,反复进行,由此达到预期的控制效果.
3.1 模型预测以采样周期Ts对系统的状态空间表达式进行离散化,引入积分环节,则离散化后的增量模型为
| $ \left\{ \begin{array}{l} \Delta \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{B}}_{\rm{u}}}\Delta \mathit{\boldsymbol{u}}\left( k \right) + {\mathit{\boldsymbol{B}}_{\rm{d}}}\Delta \mathit{\boldsymbol{d}}\left( k \right),\\ {y_{\rm{c}}}\left( k \right) = {\mathit{\boldsymbol{C}}_{\rm{c}}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {y_{\rm{c}}}\left( {k - 1} \right). \end{array} \right. $ | (12) |
式中:A =ecATs,Bu=∫0TsecAτds· Bcu,
| $ {\mathit{\boldsymbol{B}}_{\rm{d}}} = \int_0^{{T_{\rm{s}}}} {{e^{{A_{\rm{c}}}\tau }}{\rm{d}}s} \cdot {\mathit{\boldsymbol{B}}_{{\rm{cd}}}},\Delta \mathit{\boldsymbol{x}}\left( k \right) = \mathit{\boldsymbol{x}}\left( k \right) - \mathit{\boldsymbol{x}}\left( {k - 1} \right), $ |
| $ \Delta \mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{u}}\left( k \right) - \mathit{\boldsymbol{u}}\left( {k - 1} \right),\Delta \mathit{\boldsymbol{d}}\left( k \right) = \mathit{\boldsymbol{d}}\left( k \right) - \mathit{\boldsymbol{d}}\left( {k - 1} \right). $ |
根据模型预测控制基本原理,定义预测时域Np小于等于控制时域Nu,并做出如下的假设:
1) 控制时域之外,控制量不变,即
| $ \Delta u\left( {k + i} \right) = 0,\;\;\;i = {N_{\rm{u}}},{N_{\rm{u}}} + 1, \cdots ,{N_{\rm{p}}} - 1. $ |
2) 可测干扰在k时刻之后不变,即
| $ \Delta d\left( {k + i} \right) = 0,\;\;\;i = 1,2, \cdots ,{N_{\rm{p}}} - 1. $ |
在当前时刻k,测量值为x (k),可以计算出Δx(k)的大小.以Δx(k)作为预测系统未来动态的起点.由输出方程式(12)可以预测k+1到k+Np时刻的状态及被控输出.
在k时刻,定义系统的预测输出为
| $ {\mathit{\boldsymbol{Y}}_{\rm{c}}}\left( {k + 1\left| k \right.} \right) = \left[ {\begin{array}{*{20}{c}} {{y_{\rm{c}}}\left( {k + 1\left| k \right.} \right)}\\ {{y_{\rm{c}}}\left( {k + 2\left| k \right.} \right)}\\ \vdots \\ {{y_{\rm{c}}}\left( {k + {N_{\rm{p}}}\left| k \right.} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\omega _{\rm{e}}}\left( {k + 1\left| k \right.} \right)}\\ {{\omega _{\rm{e}}}\left( {k + 2\left| k \right.} \right)}\\ \vdots \\ {{\omega _{\rm{e}}}\left( {k + {N_{\rm{p}}}\left| k \right.} \right)} \end{array}} \right], $ |
其中,yc(k+Np|k)表示k时刻对k+Np时刻系统输出的预测.
控制输入序列ΔU(k)为
| $ \Delta \mathit{\boldsymbol{U}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{u}}\left( {k\left| k \right.} \right)}\\ {\Delta \mathit{\boldsymbol{u}}\left( {k + 1\left| k \right.} \right)}\\ \vdots \\ {\Delta \mathit{\boldsymbol{u}}\left( {k + {N_{\rm{u}}} - 1\left| k \right.} \right)} \end{array}} \right], $ |
其中
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{u}}\left( {k + i\left| k \right.} \right) = \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{T}}_{\rm{g}}}\left( {k + i\left| k \right.} \right)}\\ {\Delta {\mathit{\boldsymbol{T}}_{\rm{m}}}\left( {k + i\left| k \right.} \right)} \end{array}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 0,1, \cdots ,{N_u} - 1. \end{array} $ |
根据模型预测控制的基本原理,对系统未来Np步输出的预测可由预测方程式(13)计算得到:
| $ \begin{array}{l} {\mathit{\boldsymbol{Y}}_{\rm{c}}}\left( {k + 1\left| k \right.} \right) = {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{x}}}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{I}}_{\rm{c}}}y\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{u}}}}\Delta \mathit{\boldsymbol{U}}\left( k \right) + {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{d}}}}\Delta \mathit{\boldsymbol{d}}\left( k \right). \end{array} $ | (13) |
从式(13)可知,基于发动机转速ωe、前排齿圈转速ωr1的当前值及未来Np步的MG1输出力矩Tg和MG2输出力矩Tm,可以预测出未来Np步的发动机转速ωe.
3.3 优化问题及反馈控制律本文研究的主要控制需求是使发动机快速启机并且在模式切换过程中整车冲击度尽可能小,即期望冲击度为0.
定义参考序列为
| $ {\mathit{\boldsymbol{R}}_{\rm{e}}}\left( {1 + k} \right) = \left[ {\begin{array}{*{20}{c}} {r\left( {k + 1} \right)}\\ {r\left( {k + 2} \right)}\\ \vdots \\ {r\left( {k + {N_{\rm{p}}}} \right)} \end{array}} \right]. $ |
式中Re(1+k)表示发动机怠速启动时的目标转速.基于以往实车数据分析可知,发动机转速达到820 r/min附近已经启动成功,考虑一定的裕量,本文令r(k+i)=900 r/min, i=1, 2, ..., Np.
优化问题定义为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{\Delta \mathit{\boldsymbol{U}}\left( k \right)} \mathit{\boldsymbol{J}}\left( {y\left( k \right),\Delta \mathit{\boldsymbol{U}}\left( k \right),{N_{\rm{u}}},{N_{\rm{p}}}} \right),\\ \mathit{\boldsymbol{J}} = {\mathit{\boldsymbol{J}}_1} + {\mathit{\boldsymbol{J}}_2},\\ {\mathit{\boldsymbol{J}}_1} = {\left\| {{\mathit{\boldsymbol{Q}}_1}\left( {{\mathit{\boldsymbol{Y}}_c}\left( {k + 1\left| k \right.} \right) - {\mathit{\boldsymbol{R}}_{\rm{e}}}\left( {k + 1} \right)} \right)} \right\|^2},\\ {\mathit{\boldsymbol{J}}_2} = {\left\| {{\mathit{\boldsymbol{Q}}_2}\Delta \mathit{\boldsymbol{U}}\left( k \right)} \right\|^2}.\\ {\rm{s}}.\;{\rm{t}}.\;{\omega _{{\rm{e}}\min }}\left( k \right) \le {\omega _{\rm{e}}}\left( k \right) \le {\omega _{{\rm{e}}\max }}\left( k \right),\\ \;\;\;\;\;{\omega _{{\rm{r1}}\min }}\left( k \right) \le {\omega _{{\rm{r1}}}} \le {\omega _{{\rm{r1}}\max }}\left( k \right),\\ \;\;\;\;\;\Delta {T_{{\rm{g}}\min }}\left( k \right) \le \Delta {T_g}\left( k \right) \le \Delta {T_{{\rm{g}}\max }}\left( k \right),\\ \;\;\;\;\;\Delta {T_{{\rm{m}}\min }}\left( k \right) \le \Delta {T_{\rm{m}}}\left( k \right) \le \Delta {T_{{\rm{m}}\max }}\left( k \right),\\ \;\;\;\;\;{T_{{\rm{g}}\min }}\left( k \right) \le {T_g}\left( k \right) \le {T_{{\rm{g}}\max }}\left( k \right),\\ \;\;\;\;\;{T_{{\rm{m}}\min }}\left( k \right) \le {T_{\rm{m}}}\left( k \right) \le {T_{{\rm{m}}\max }}\left( k \right). \end{array} \right. $ |
式中:J1表示模式切换时发动机快速启动要求;Q1表示权重矩阵,Q1越大,该项所占比重越大,发动机启动越快;J2表示电机MG1和电机MG2转矩的变化;Q2表示权重矩阵;Q2越大,MG1和MG2转矩变化越平缓,从而实现发动机的平稳启动,保证系统平顺性;ΔTg(k)和ΔTm(k)表示电机MG1和电机MG2转矩的变化率,由发动机和电机物理特性可知,发动机、电机的转速、转矩以及变化率均受到一定约束限制.
根据前文预测模型输出方程,上述优化问题可以进一步转化为二次规划问题,即
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{\Delta \mathit{\boldsymbol{U}}\left( k \right)} \frac{1}{2} {\varDelta} \mathit{{U}}{\left( {^k} \right)^{\rm{T}}}\mathit{\boldsymbol{H}} {\varDelta} \mathit{\boldsymbol{U}}\left( k \right) + \mathit{\boldsymbol{G}}{\left( {^k + 1\left| k \right.} \right)^{\rm{T}}} {\varDelta} \mathit{\boldsymbol{U}}\left( k \right),\\ {\rm{s}}.\;{\rm{t}}.\;{\mathit{\boldsymbol{C}}_{\rm{u}}} {\varDelta} \mathit{\boldsymbol{U}}\left( k \right) \ge b\left( {k + 1\left| k \right.} \right). \end{array} \right. $ |
式中:H =2(Sc, uT Q1T Q1 Sc, u+ Q2T Q2),
| $ \mathit{\boldsymbol{G}}\left( {k + 1\left| k \right.} \right) = - 2\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{u}}}^{\rm{T}}\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{Q}}_1}{\mathit{\boldsymbol{E}}_{\rm{p}}}\left( {k + 1\left| k \right.} \right), $ |
| $ {\mathit{\boldsymbol{E}}_{\rm{p}}}\left( {k + 1\left| k \right.} \right) = {\mathit{\boldsymbol{R}}_{\rm{e}}}\left( {k + 1} \right) - {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{x}}}} {\varDelta} \mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{d}}}} {\varDelta} \mathit{\boldsymbol{d}}\left( k \right) - {I_{\rm{c}}}\mathit{\boldsymbol{y}}\left( k \right), $ |
| $ {\mathit{\boldsymbol{C}}_{\rm{u}}} = {\left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{I}}}&\mathit{\boldsymbol{I}}&{ - {\mathit{\boldsymbol{L}}^{\rm{T}}}}&{{\mathit{\boldsymbol{L}}^{\rm{T}}}}&{ - \mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{u}}}^{\rm{T}}}&{\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{u}}}^{\rm{T}}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{Y}}_{\min }}\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}} {{y_{\min }}\left( {k + 1} \right)}\\ {{y_{\min }}\left( {k + 2} \right)}\\ \vdots \\ {{y_{\min }}\left( {k + {N_p}} \right)} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{Y}}_{\max }}\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}} {{y_{\max }}\left( {k + 1} \right)}\\ {{y_{\max }}\left( {k + 2} \right)}\\ \vdots \\ {{y_{\max }}\left( {k + {N_p}} \right)} \end{array}} \right], $ |
| $ \begin{array}{l} \mathit{\boldsymbol{b}}\left( {k + 1\left| k \right.} \right) = \\ \left[ {\begin{array}{*{20}{c}} { - \Delta {\mathit{\boldsymbol{u}}_{\max }}\left( k \right)}\\ \vdots \\ { - \Delta {\mathit{\boldsymbol{u}}_{\max }}\left( {k + {N_u} - 1} \right)}\\ {\Delta {\mathit{\boldsymbol{u}}_{\min }}\left( k \right)}\\ \vdots \\ {\Delta {\mathit{\boldsymbol{u}}_{\min }}\left( {k + {N_u} - 1} \right)}\\ {\mathit{\boldsymbol{u}}\left( {k - 1} \right) - {\mathit{\boldsymbol{u}}_{\max }}\left( k \right)}\\ \vdots \\ {\mathit{\boldsymbol{u}}\left( {k - 1} \right) - {\mathit{\boldsymbol{u}}_{\max }}\left( {k + {N_u} - 1} \right)}\\ {{\mathit{\boldsymbol{u}}_{\min }}\left( k \right) - \mathit{\boldsymbol{u}}\left( {k - 1} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{u}}_{\min }}\left( {k + {N_u} - 1} \right) - \mathit{\boldsymbol{u}}\left( {k - 1} \right)}\\ {\mathit{\boldsymbol{IY}}\left( k \right) + {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{x}}}}\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{d}}}}\Delta \mathit{\boldsymbol{d}}\left( k \right) - {\mathit{\boldsymbol{Y}}_{\max }}\left( {k + 1} \right)}\\ {{\mathit{\boldsymbol{Y}}_{\min }}\left( {k + 1} \right) - {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{x}}}}\Delta \mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{S}}_{{\rm{c}},{\rm{d}}}}\Delta \mathit{\boldsymbol{d}}\left( k \right) - \mathit{\boldsymbol{IY}}\left( k \right)} \end{array}} \right], \end{array} $ |
I为单位矩阵,L为各元素都为单位矩阵的下三角矩阵.
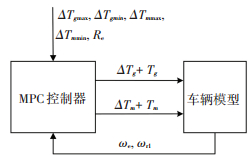
显然上式中H ≥0,所以该优化问题存在最优解.根据上述控制输入以及状态变量的约束,利用二次规划方法求解获得最优控制序列Δ U (k),利用优化控制序列的第一个元素构造控制输入信号,并应用于被控系统,建立模型预测控制器,在每个采样过程重复上述优化计算过程,直至模式切换完成.将MPC控制器放置在车辆控制策略EVT模式子模块中,MPC控制器结构如图 6所示.车辆进入EVT模式时,当发动机转速小于发动机怠速时应用MPC控制器进行控制,直至发动机顺利启动后,电机MG1转矩和电机MG2转矩为MPC控制器的输出参数.
|
图 6 MPC控制器结构 Figure 6 MPC controller structure |
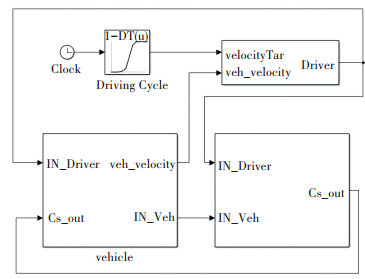
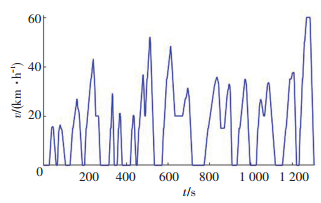
利用实车历史数据建立的基于数据驱动的发动机动态模型、电机模型和一阶RC电池模型等部件模型,在Matlab/Simulink平台搭建整车动态模型.所建立的离线仿真模型如图 7所示,包括行驶工况、驾驶员模型、车辆模型和控制策略4个部分.其中行驶工况采用中国典型城市工况,如图 8所示.
|
图 7 离线仿真模型 Figure 7 Offline simulation model |
|
图 8 中国典型循环工况 Figure 8 Typical urban driving cycle in China |
整车参数如表 1所示,系统动力学仿真所需参数如表 2所示,PID控制参数以及MPC控制器仿真参数如表 3所示.
| 表 1 整车参数 Table 1 Vehicle parameters |
| 表 2 系统动力学参数 Table 2 System dynamics parameters |
| 表 3 仿真参数 Table 3 Simulation parameters |
针对发动机启动过程的动态协调控制,当接受到模式切换请求时,首先进入启机过程的瞬态控制模式,直到发动机正常输出转矩,且发动机转速大于目标怠速时,系统进入由稳态PID控制的EVT模式.为验证MPC控制器的动态协调控制效果,将采用闭环PID控制与被动切换作为对比,对3种控制方法的计算仿真结果进行比较分析.
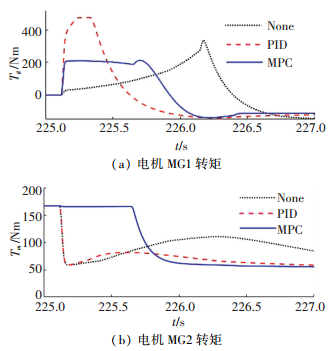
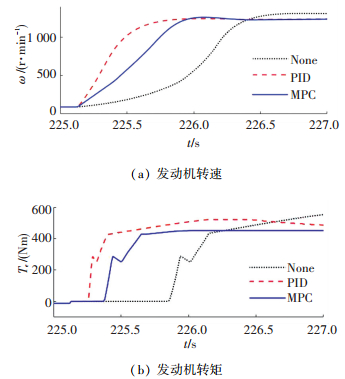
在模式切换过程中,3种控制方法下的电机MG1和MG2的转矩变化,以及发动机转矩、转速的变化,分别如图 9、图 10所示.
|
图 9 电机转矩对比 Figure 9 Comparison of MG1 and MG2 torque |
|
图 10 发动机转速和转矩对比 Figure 10 Comparison of engine speed and torque |
从图 9中可见,在被动切换下,接收到切换命令后,因为没有反馈机制,电机MG1缓慢输出转矩,电机MG2转矩突降,这样极易引起系统冲击,从图 10(a)中可以看到发动机用时将近1 s才达到怠速.当发动机转速达到怠速时,车辆切换到EVT模式,此时系统的控制方法变为稳态PID控制,因为MG1转矩的控制规则改变,导致图 9(a)中电机MG1转矩曲线出现了“尖点”.而在PID控制方法下,接收到切换命令后,电机MG1立刻输出转矩,快速提升到峰值转矩附近,同时,由于在启动过程中未能准确估计发动机输出扭矩,电机MG2的转矩出现波动,电机MG1和MG2转矩的变化导致系统输出转矩的波动,从而引起系统冲击.从图 10(a)中可见,在PID控制方法下,发动机启动较快,大约用时0.3 s即达到怠速.如图 9所示,采用MPC控制器,有效抑制电机MG1转矩的快速变化,使MG1转矩上升平稳,而通过MPC控制器预测得到的电机MG2转矩,也能在启动时刻有效补偿启机造成的负向冲击.如图 10(a)所示,采用MPC控制器以后发动机的启机耗时约0.5 s,相比PID控制方法有明显的增加,但该启机时间也完全能满足客车的性能要求.
对比3种控制方法下的冲击度和车速变化,如图 11和图 12所示.在被动切换下,由于电机MG1的转矩缓慢提升以及电机MG2转矩的波动,导致整车产生负方向冲击,虽然冲击度波动较小,但发动机启动用时较长,车速长时间内无法满足驾驶员需求.在PID控制方法下,模式切换时,由于电机MG1转矩的快速提升,以及电机MG2转矩的波动,导致整车出现明显的负方向冲击,车速也未能良好跟随驾驶员需求,变化速率显著降低.因为电机MG2与车轮直接耦合,模式切换后,由于未能准确估计发动机输出转矩,电机MG2转矩波动,系统的输出转矩小于需求转矩,导致车速短时间内出现了下降.发动机开始喷油(根据实车数据定义发动机转速达到440 r/min开始喷油输出转矩)时,电机MG2未能与发动机转矩有效协调,系统出现明显的正向冲击,整个启动过程中的系统平顺性较差.而采用MPC控制器,模式切换时的峰值冲击度骤减,从PID控制时的15.87 m·s-3下降至4.71 m·s-3.车速基本保持一致的变化速率,在发动机喷油时刻,电机MG2主动降低转矩,也减小了系统的正向冲击度.
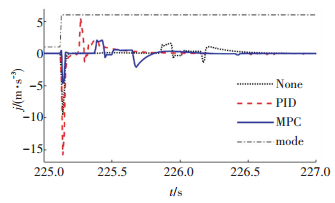
|
图 11 冲击度比较 Figure 11 Jerk comparison |

|
图 12 车速对比 Figure 12 Vehicle speed comparison in simulation |
1) 本文提出一种基于模型预测控制的模式切换过程中转矩动态补偿控制方法,并设计一种基于数据驱动的模型预测控制器.仿真结果表明,在保证动力性的前提下,相比于PID控制和被动切换,提出的模型预测控制器有效地减小了整车模式切换时的峰值冲击度,并且符合德国汽车行业中冲击度的推荐值——| j |≤10 m·s-3[15],同时实现了发动机的正常启动,保证了汽车模式切换时的平顺性,提高了模式切换品质.
2) 本文以行星式混合动力客车为研究对象建立系统仿真模型,提出的模型预测控制方法以及优化问题对其他构型的混合动力车辆的起步协调控制、控制目标及参数的调整同样具有一定的借鉴意义和参考作用.
| [1] |
陈清泉, 孙逢春, 祝嘉光. 现代电动汽车技术[M]. 北京: 北京理工大学出版社, 2002. CHEN Qingquan, SUN Fengchun, ZHU Jiaguang. Modern electric vehicle technology[M]. Beijing: Beijing Institute of Technology Press, 2002. |
| [2] |
严运兵.并联混合动力电动汽车的动态控制研究[D].武汉: 武汉理工大学, 2008 YAN Yunbing. Study on the dynamic control in parallel hybrid electric vehicle[D]. Wuhan: Wuhan University of Technology, 2008 http://cdmd.cnki.com.cn/article/cdmd-10497-2008160093.htm |
| [3] |
CHOI W, KANG J, HONG S, et al. Development of a control algorithm to reduce torque variation for the dual mode HEV during mode change[C]// Vehicle Power and Propulsion Conference. Chicago: IEEE, 2011: 1
|
| [4] |
童毅.并联式混合动力系1统动态协调控制问题的研究[D].北京: 清华大学, 2004 TONG Yi. Study on the coordinated control issue in parallel hybrid electric system[D]. Beijing: Tsinghua University, 2004 http://cdmd.cnki.com.cn/article/cdmd-10003-2005036031.htm |
| [5] |
郑萍, 白金刚, 宋志翌, 等. 混合动力汽车用复合结构电机及其关键技术发展[J]. 哈尔滨工业大学学报, 2016, 48(3): 1. ZHENG Ping, BAI Jingang, SONG Zhiyi, et al. Development of the compound-structure electrical machine and its key technologies for hybrid electric vehicles[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 1. DOI:10.11918/j.issn.0367-6234.2016.03.001 |
| [6] |
温博轩, 王伟达, 项昌乐, 等. 混联式混合动力系统动态响应协调控制[J]. 哈尔滨工业大学学报, 2016, 48(1): 72. WEN Boxuan, WANG Weida, XIANG Changle, et al. Torque coordinated control for the multi power in parallel-series HEV[J]. Journal of Harbin Institute of Technology, 2016, 48(1): 72. DOI:10.11918/j.issn.0376-6234.2016.01.011 |
| [7] |
HWANG H Y. Minimizing seat track vibration that is caused by the automatic start/stop of an engine in a power-split hybrid electric vehicle[J]. Journal of Vibration & Acoustics, 2013, 135(6): 061007. |
| [8] |
TOMURA S, ITO Y, KAMICHI K, et al. Development of vibration reduction motor control for series-parallel hybrid system[C]// SAE 2006 World Congress & Exhibition, 2006
|
| [9] |
ZHU F, CHEN L, YIN C, et al. Dynamic modelling and systematic control during the mode transition for a multi-mode hybrid electric vehicle[J]. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, 2013, 227(7): 1007. DOI:10.1177/0954407013477027 |
| [10] |
朱福堂.单电机多模式混合动力系统的架构设计分析与模式切换研究[D].上海: 上海交通大学, 2014 ZHU Futang. Architecture design, analysis and mode transition research of a multi-mode hybrid powertrain using a single electric machine[D]. Shanghai: Shanghai Jiaotong University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10248-1015807832.htm |
| [11] |
SYED F U, KUANG M L, YING H. Active damping wheel-torque control system to reduce driveline oscillations in a power-split hybrid electric vehicle[J]. IEEE Transactions on Vehicular Technology, 2009, 58(9): 4769. DOI:10.1109/TVT.2009.2025953 |
| [12] |
WANG J, RAKHA H A. Fuel consumption model for heavy duty diesel trucks: Model development and testing[J]. Transportation Research Part D Transport & Environment, 2017, 55: 127. |
| [13] |
SUN J, XING G, LIU X, et al. A novel torque coordination control strategy of a single-shaft parallel hybrid electric vehicle based on model predictive control[J]. Mathematical Problems in Engineering, 2015, 2015(1): 1. |
| [14] |
FROISY J B. Model predictive control: past, present and future[J]. Isa Transactions, 1999, 33(3): 235. |
| [15] |
杜波, 秦大同, 段志辉, 杨文辉, 彭志远.新型混合动力汽车动力切换动态过程分析[J].汽车工程, 2011, 33(12): 1018 DU Bo, QIN Datong, DUAN Zhihui, et al. An analysis on the power switching dynamic process in a new type of HEV[J]. Automotive Engineering, 2011, 33(12): 1018 http://d.wanfangdata.com.cn/Periodical/qcgc201112003 |
 2019, Vol. 51
2019, Vol. 51


