2. 中国空间技术研究院, 北京 100094
2. China Academy of Space Technology, Beijing 100094, China
工程结构优化设计往往需要考虑强度、刚度和稳定性等多种设计要求,这些要求一般以目标或约束函数的形式体现在优化模型中.结构优化传统数学模型中的隐式函数通常涉及平衡方程和广义特征值等问题的求解,优化模型是非凸的.当特征方程出现重根时,不存在常规意义的导数信息,无法直接计算特征值的灵敏度.全局稳定约束也存在类似问题,并且由于几何刚度矩阵与杆件内力相关,其性态更加复杂.此类复杂优化模型的求解往往十分困难,有时不得不借助启发式算法[1-5].
半定规划(semidefinite programming, SDP)是20世纪90年代发展起来的数学规划分支,是经典的线性与非线性规划在矩阵空间中的推广[6].半定规划的对称矩阵变量和矩阵不等式相比传统形式的变量和约束更加一般化,线性规划、线性约束二次规划、二次约束二次规划等都是半定规划的特例[7-8],因此半定规划具有更强的问题描述能力,很多非线性优化问题都可以通过半定规划进行建模[9].另外,线性半定规划是凸优化问题[10],求解该问题的内点法在理论和实践中都表现出了极高的效率[7];对非线性半定规划,目前也有增广拉格朗日函数法、序列半定规划法、原对偶内点法等多种求解算法可用[11].基于上述两点,半定规划方法在很多工程和科学领域都有广泛应用.
20世纪90年代末,半定规划开始应用于结构优化领域.Ben-Tal等[12]基于半定规划考虑载荷不确定性,进行柔度约束下的鲁棒桁架拓扑优化设计.张家凡等[13]构造了体积约束结构整体刚度最大化问题的半定规划列式.Ohsaki等[14]将基频约束表示为矩阵不等式,建立了体积最小化问题的半定规划模型.Achtziger等[15]将柔度和频率约束转换成半定矩阵约束,将基频最大化问题转化为双线性半定规划形式.李东泽等[16-17]在设计卫星主桁架时,用半定规划法对柔度和基频约束下的结构体积最小化问题进行了求解和讨论. Ko vara等[18-19]将考虑结构全局稳定约束的优化问题建模为一个非凸半定规划问题.Ni等[20]简要讨论了用非线性半定规划处理频率约束刚架结构拓扑优化的相关问题.对相同的问题,Yamada等[21]则使用连续松弛方法处理半定形式的频率约束.上述研究主要侧重于单一的某种全局性约束的处理,少有考虑多种工程约束的综合性建模研究.
本文从结构优化的一般性模型出发,基于已有文献对部分约束的等价半定转化,首先给出了考虑特定约束桁架拓扑优化问题的线性半定规划对偶模型的标准形式,并说明了标准模型中变量和系数的推导过程.通过转化,将传统的非线性非凸模型转化为凸的半定规划模型,并能有效处理多重特征值灵敏度分析问题.然后以全局稳定约束和应力约束为例,说明了两类非线性约束的半定近似方法,将非线性模型转化为统一的近似模型并给出序列半定近似求解算法.统一模型能够考虑较为全面的约束类型,基于序列近似的求解算法则能利用半定模型和算法的良好特性,提高了求解桁架优化问题的能力.模型的标准化和近似处理为直接调用半定规划求解器进行问题求解奠定了基础,处理过程还可为其他结构优化问题的半定规划建模提供参考.
1 结构优化问题本文考虑的不等式约束优化问题可写为:
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&{f\left( \mathit{\boldsymbol{x}} \right),}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}}&{{g_i}\left( \mathit{\boldsymbol{x}} \right) \le 0,\quad i = 1, \cdots ,k;}\\ {}&{\mathit{\boldsymbol{L}} \le \mathit{\boldsymbol{x}} \le \mathit{\boldsymbol{U}}.} \end{array}} \right. $ | (1) |
式中:x =[x1, x2, …, xm]T为优化变量;f(x)为目标函数;gi(x)为不等式约束函数,其数量为k;m维列向量U、L分别为变量x的上、下限.
对结构优化问题,目标及约束通常包含某些与结构特性相关的指标,这些指标多是优化变量的隐式非线性函数,一般通过有限元法求解复杂的等式原理方程得到具体数值.该过程即为结构分析过程.
绝大多数结构优化问题是单目标优化问题,f(x)为标量函数.这里引入附加变量η及不等式约束g0(x)=f(x)-η≤0,则原优化问题(1)等价于:
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&\eta \\ {{\rm{s}}.{\rm{ t}}{\rm{. }}}&{{g_i}\left( \mathit{\boldsymbol{x}} \right) \le 0,\quad i = 0,1, \cdots ,k;}\\ {}&{L \le x \le \mathit{\boldsymbol{U}}.} \end{array}} \right. $ | (2) |
该模型中,目标函数η是简单的线性形式,要考虑的结构特性则均体现在约束函数中,便于统一处理.一般来说,每个约束函数gi(x)中包含的结构特性指标都是通过求解对应的原理方程(如静态平衡方程、频率特征值方程或者简单的求和函数等)得到的,优化模型中通常不列出这些原理方程.
2 桁架结构优化部分约束的等价半定形式半定规划理论用于桁架结构优化问题建模时,某些全局结构特性(如柔度、基频和全局稳定性等)的传统不等式约束gi(x)≤0及其原理方程可转化为等价的矩阵半定形式的约束Gj(x)
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&\eta \\ {{\text{s}}.{\text{t}}.}&{{g_i}\left( \mathit{\boldsymbol{x}} \right) \leqslant 0,\quad i \in {\mathit{\boldsymbol{I}}_{{\text{scalar}}}};} \\ {}&{{\mathit{\boldsymbol{G}}_j}\left( \mathit{\boldsymbol{x}} \right) \underline \succ \mathit{\boldsymbol{O}},\quad j \in {\mathit{\boldsymbol{J}}_{{\text{SD}}}};} \\ {}&{\mathit{\boldsymbol{L}} \leqslant \mathit{\boldsymbol{x}} \leqslant \mathit{\boldsymbol{U}}.} \end{array}} \right. $ | (3) |
式中:Iscalar为保留传统形式标量约束的指标集;JSD为转化为等价的半定形式约束的指标集.
首先给出桁架结构变量下限约束、体积约束、柔度约束、基频约束和全局稳定约束的半定形式.
2.1 变量下限约束在桁架结构拓扑优化问题中,一般仅要求杆件的横截面积不小于零.若以杆件体积向量t =[t1, …, tm]T为设计变量(m为桁架中杆件总数),则变量非负要求ti≥0, i=1, …, m可等价写为
| $ {\text{diag}}\left\{ \mathit{\boldsymbol{t}} \right\} \underline \succ \mathit{\boldsymbol{O}}, $ |
式中diag{t}为以t中各元素为对角线元素的对角矩阵(若t为多个方阵,则diag{t}为以这些方阵为对角块的分块对角矩阵).注意这里应用了对角矩阵的特征值为其对角元素的性质以及矩阵半定的定义.
2.2 体积约束轻量化是航空航天结构设计的一个重要特点.若结构材料具有均一密度ρ,结构质量约束可等价表示为体积约束V≤V,其中
| $ - \sum\limits_{i = 1}^m {{t_i}} + \bar V \geqslant 0. $ |
结构柔度C也称为柔顺度,一般定义为外载荷f在其引起的位移u上所做的虚功[22],即C=fTu(也有文献定义C=fTu/2,进行算例对比时需注意).受载时的柔度值越小,结构抵抗静态变形的能力就越强.记C为许用柔度上限,则由Schur补定理[6],柔度约束C≤C和平衡方程f=Ku (其中K为结构刚度矩阵)可等价表述为矩阵半定的形式:
| $ \left[ {\begin{array}{*{20}{l}} {\bar C}&{{\mathit{\boldsymbol{f}}^{\text{T}}}} \\ \mathit{\boldsymbol{f}}&\mathit{\boldsymbol{K}} \end{array}} \right] \underline \succ \mathit{\boldsymbol{O}}. $ |
结构的广义特征值λ一般可通过求解如下动力学方程得到[23]:
| $ \mathit{\boldsymbol{K \boldsymbol{\varPhi} }} - \lambda \left( {{\mathit{\boldsymbol{M}}_{\text{s}}} + {\mathit{\boldsymbol{M}}_0}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = 0, $ | (4) |
式中刚度矩阵K和结构相关质量矩阵Ms分别为变量t的函数,非结构质量矩阵M0为常值矩阵.
将式(4)的最小广义特征值记作λmin,则结构基频f0=
根据广义Rayleigh商相关理论,动力学方程(4)和基频约束λmin≥λ可表示为等价的半定约束形式:
| $ \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{t}} \right) - \underline \lambda \left( {{\mathit{\boldsymbol{M}}_{\text{s}}}\left( \mathit{\boldsymbol{t}} \right) + {\mathit{\boldsymbol{M}}_0}} \right) \underline \succ \mathit{\boldsymbol{O}}. $ |
当结构的弹性刚度不足导致结构整体发生屈曲时,称结构出现全局不稳定.结构承受外部载荷fr=λr f0(其中f0为载荷模式,λr为载荷因子)时,由广义特征值方程[23]:
| $ \left( {\mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{t}} \right) + {\lambda _{\text{r}}}{\mathit{\boldsymbol{K}}_{\text{G}}}\left( {{\mathit{\boldsymbol{f}}_0},\mathit{\boldsymbol{t}}} \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\text{G}}} = {\bf{0}}, $ | (5) |
求得的最小正特征值λcr即为结构全局稳定分析的临界屈曲载荷因子,对应临界屈曲载荷为fcr=λcrf0.当结构所受载荷大于其临界载荷时,即发生全局不稳定现象.式(5)中KG为桁架结构的几何刚度矩阵.
全局稳定约束要求实际载荷的载荷因子λG小于结构的临界屈曲载荷因子,即λG≤λcr.根据文献[19]中给出的引理,可将全局稳定约束和稳定性方程(5)表述为等价的半定约束形式:
| $ \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{t}} \right) + {\lambda _{\text{G}}}{\mathit{\boldsymbol{K}}_{\text{G}}}\left( {{\mathit{\boldsymbol{f}}_0},\mathit{\boldsymbol{t}}} \right) \underline \succ \mathit{\boldsymbol{O}}. $ |
本文给出的桁架结构拓扑优化中的部分约束及其等价半定形式见表 1.
| 表 1 桁架结构拓扑优化中部分约束及其等价半定形式 Tab. 1 Some constraints in truss topology optimization and their equivalent semidefinite forms |
对桁架结构, 矩阵K (t)和Ms(t)均为变量t的线性矩阵函数,因此表 1中给出的前3类约束的半定形式均为变量t的线性矩阵不等式;当基频下限为常值时,基频约束的半定形式也是线性的.考虑到优化模型(3)中目标函数为标量函数,仅包含这4类半定约束的桁架结构优化模型是线性半定规划问题,且是凸优化问题,其局部最优解即全局最优解.
3.1 线性半定规划及其对偶问题的标准形式线性半定规划原问题的标准数学形式为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{\mathit{\boldsymbol{X}} \in {\mathscr{I}^n}} }&{\mathit{\boldsymbol{C}} \cdot \mathit{\boldsymbol{X}},} \\ {{\text{s}}.\;{\text{t}}.}&{{\mathit{\boldsymbol{A}}_i} \cdot \mathit{\boldsymbol{X}} = {b_i},i = 1, \cdots ,m;\mathit{\boldsymbol{X}} \underline \succ \mathit{\boldsymbol{O}}.} \end{array}} \right. $ | (6) |
式中: X为对称矩阵变量;
问题(6)中变量为矩阵形式,不便于应用.由拉格朗日对偶原理可导出原问题(6)的对偶问题的表达式[6],进一步可写成如下的标准数学形式:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_y }&{{\mathit{\boldsymbol{b}}^{\text{T}}}\mathit{\boldsymbol{y}},} \\ {{\text{s}}.\;{\text{t}}.}&{\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{C}} + \sum\limits_{i = 1}^m {{y_i}} {\mathit{\boldsymbol{A}}_i} \underline \succ \mathit{\boldsymbol{O}},} \end{array}} \right. $ | (7) |
式中y为新的向量形式的变量.很多高效的线性半定规划求解器都可以直接求解优化问题(7),下面的建模过程即是将桁架拓扑优化模型转化为此种对偶规划问题,同时给出变量和系数的显式表达式.
3.2 桁架拓扑优化的线性半定规划模型本文将桁架拓扑优化问题的数学模型表述为式(7)的形式.这里引入目标函数的标量上限η,通过最小化η来最小化目标函数.以柔度最小化问题为例,考虑4类线性半定约束的桁架结构优化模型为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{t \in {{\bf{R}}^{\rm m}},\tau \in {\bf{R}}} \tau ,\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{l}} \tau &{{{\boldsymbol{f}}^{\rm{T}}}}\\ {\boldsymbol{f}}&{\boldsymbol{K}(\mathit{\boldsymbol{t}})} \end{array}} \right]\underline \succ {\boldsymbol{O}},\\ \;\;\;\;\;\;\;\;\;\;\;{\boldsymbol{K}}({\boldsymbol{t}}) - \underline \lambda \left( {{{\boldsymbol{M}}_{\rm{s}}}(t) + {{\boldsymbol{M}}_0}} \right)\underline \succ {\boldsymbol{O}},\\ \;\;\;\;\;\;\;\;\;\;\; - \sum\limits_{i = 1}^m {{t_i}} + \bar V \ge 0,\\ \;\;\;\;\;\;\;\;\;\;\;{\rm{diag}}\;\left\{ {\boldsymbol{t}} \right\}\underline \succ {\boldsymbol{O}}. \end{array} \right. $ | (8) |
注意,式中的附加变量η取为τ,表示柔度上限.由表 1中的约束等价关系可知,条件C≤τ已包含在模型(8)的第1个矩阵不等式中.根据半定矩阵的性质,有限个实对称矩阵半定等价于以其为对角块的分块对角矩阵半定[6],故模型(8)可等价表示为
| $ \left\{ \begin{gathered} \mathop {\min }\limits_{t \in {{\bf{R}}^m},\tau \in {\bf{R}}} \;\;\;\;\;\tau = {\mathit{\boldsymbol{b}}^{\text{T}}}\mathit{\boldsymbol{y}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\hfill \\ {\text{s}}{\text{.}}\;{\text{t}}{\text{. }}\quad \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{t}},\tau } \right) = \mathit{\boldsymbol{C}} + \sum\limits_{i = 1}^{m + 1} {{y_i}} {\mathit{\boldsymbol{A}}_i} = {\rm diag} \left\{ {\left[ {\begin{array}{*{20}{c}} \tau &{{\mathit{\boldsymbol{f}}^{\text{T}}}} \\ \mathit{\boldsymbol{f}}&{\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{t}})} \end{array}} \right]} \right., \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{t}}) - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\lambda } \left( {{\mathit{\boldsymbol{M}}_{\text{s}}}(\mathit{\boldsymbol{t}}) + {\mathit{\boldsymbol{M}}_0}} \right), \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \sum\limits_{i = 1}^m {{t_i}} + \overline V , {\rm diag} \{ \mathit{\boldsymbol{t}}\} } \right] \underline \succ \mathit{\boldsymbol{O}}\mathit{\boldsymbol{.}} \hfill \\ \end{gathered} \right. $ | (9) |
对照标准模型(7),并结合K (t)、Ms(t)关于t的线性表达式,可确定模型中相关变量和矩阵的具体表达式,详见表 2.矩阵Ai, i=1, …, m+1和C中各分块位置与模型(8)、(9)中约束函数的排列顺序对应.若考虑体积最小化问题,则仅需将柔度最小化模型约束函数S(t, τ)中的τ替换为柔度上限C,将体积上限V替换为附加变量υ,并取目标函数为η=υ即可.该问题相关变量和矩阵的表达式同样列于表 2中.由于引入了附加变量η,变量维度均变为m+1.以标准形式表述的桁架结构优化模型可高效求解.
| 表 2 线性半定规划模型中的变量和系数 Tab. 2 Variables and coefficients in linear semidefinite programming model |
表 1的各类半定约束中,当以基频最大为优化目标时,基频下限为变量,基频约束中包含变量乘积项,是一个双线性矩阵不等式;几何刚度矩阵KG是设计变量t的非线性矩阵函数,故全局稳定约束是一个更加复杂的非线性矩阵不等式.优化问题求解时,需将非线性半定约束转化为半定规划求解器能够处理的线性或其他近似形式.此外,桁架优化模型(3)中还存在常规非线性约束gi(x)≤0,也需将其纳入半定规划问题的求解框架中.
标准形式的半定规划问题可使用SeDuMi[24]、SDPT3[25]、PENLAB[26]等求解器进行求解.前两者是线性半定规划求解器.PENLAB是非线性半定规划求解器,可直接处理线性、双线性或多项式形式的矩阵半定约束,但为取得较好的求解效果,应尽量使用简单的半定约束形式.
4.1 非线性约束的近似处理 4.1.1 非线性半定约束的处理考虑到半定规划求解器的求解能力,需将优化问题(3)中的约束函数Gj(x)近似为线性、双线性或多项式矩阵函数
将载荷模式f0取为当前载荷f,定义全局稳定约束的矩阵约束函数为
| $ \begin{gathered} {\mathit{\boldsymbol{X}}_{\text{G}}}(\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}) = \mathit{\boldsymbol{K}}(\mathit{\boldsymbol{t}}) + {\lambda _{\text{G}}}{\mathit{\boldsymbol{K}}_{\text{G}}}\left( {{\mathit{\boldsymbol{f}}_0},\mathit{\boldsymbol{t}}} \right) = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{K}}(\mathit{\boldsymbol{t}}) + {\lambda _{\text{G}}}\sum\limits_{i = 1}^m {{q_i}} \left( {\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}} \right){\mathit{\boldsymbol{K}}_{{\text{G,}}i}}, \hfill \\ \end{gathered} $ |
其中常值矩阵KG, i的表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{K}}_{{\rm{G}},i}} = \frac{1}{{{l_i}}}\left( {\left( { - {\mathit{\boldsymbol{e}}_{n,p}} + {\mathit{\boldsymbol{e}}_{n,q}}} \right){{\left( { - {\mathit{\boldsymbol{e}}_{n,p}} + {\mathit{\boldsymbol{e}}_{n,q}}} \right)}^{\rm{T}}}} \right) \otimes \\ \;\;\;\;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{I}}_3} - {\mathit{\boldsymbol{b}}_{i0}}\mathit{\boldsymbol{b}}_{i0}^{\rm{T}}} \right), \end{array} $ |
qi(f, t)为第i杆内力,其表达式为
| $ {q_i}\left( {\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}} \right) = \frac{{{E_i}{t_i}}}{{l_i^2}}\mathit{\boldsymbol{b}}_{iE}^{\rm{T}}\mathit{\boldsymbol{K}}{\left( \mathit{\boldsymbol{t}} \right)^{ - 1}}\mathit{\boldsymbol{f}}. $ |
式中:Ei为第i杆的弹性模量;li为第i杆的杆长;biET=(-en, p+en, q)T⊗[cos θxix, cos θxiy, cos θxiz],这里的θxix、θxiy、θxiz分别为杆件i局部坐标系x轴与全局坐标系x、y、z轴之间的夹角.
XG的非线性源于内力qi(f, t).为线性化XG,参照文献[27]引入杆件内力近似策略.在t=t0处对函数qi (f, t)进行线性化,得到其线性近似函数为
| $ {{\tilde q}_i}\left( {\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}} \right) = {q_i}\left( {\mathit{\boldsymbol{f}},{\mathit{\boldsymbol{t}}_0}} \right) + {\left. {\sum\limits_{j = 1}^m {\frac{{\partial {q_i}}}{{\partial {t_j}}}} } \right|_{t = {t_0}}}\left( {{t_j} - {t_{j,0}}} \right), $ |
则全局稳定约束的线性近似矩阵函数为
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde X}}}_{\rm{G}}}\left( {\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}} \right) = \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{t}} \right) + {\lambda _{\rm{G}}}\sum\limits_{i = 1}^m {{{\tilde q}_i}\left( {\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}} \right){\mathit{\boldsymbol{K}}_{{\rm{G}},i}}} = }\\ {{{\mathit{\boldsymbol{\tilde X}}}_{{\rm{G}},{\rm{0}}}} + \sum\limits_{j = 1}^m {{t_i}{{\mathit{\boldsymbol{\tilde X}}}_{{\rm{G}},i}}} ,} \end{array} $ |
其中常值矩阵和系数矩阵分别为:
| $ {{\mathit{\boldsymbol{\tilde X}}}_{{\rm{G}},{\rm{0}}}} = {\lambda _{\rm{G}}}\sum\limits_{i = 1}^m {\left( {{q_i}\left( {\mathit{\boldsymbol{f}},{\mathit{\boldsymbol{t}}_0}} \right) - \sum\limits_{j = 1}^m {\frac{{\partial {q_i}}}{{\partial {t_j}}}\left| {_{t = {t_0}}} \right.{t_{j,0}}} } \right){\mathit{\boldsymbol{K}}_{{\rm{G}},i}}} , $ |
| $ {{\mathit{\boldsymbol{\tilde X}}}_{{\rm{G}},i}} = {\mathit{\boldsymbol{K}}_i} + {\lambda _{\rm{G}}}\sum\limits_{j = 1}^m {\frac{{\partial {q_j}}}{{\partial {t_i}}}\left| {_{t = {t_0}}{\mathit{\boldsymbol{K}}_{{\rm{G}},j}}} \right.} . $ |
由刚度矩阵K的线性表达式,可得∂K -1/∂ti=-K -1KiK -1,因此内力函数的灵敏度为
| $ \frac{{\partial {q_i}}}{{\partial {t_j}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{E_i}}}{{l_i^2}}\mathit{\boldsymbol{b}}_{iE}^{\rm{T}}\left( {{\mathit{\boldsymbol{K}}^{ - 1}} - {t_i}{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{K}}^{ - 1}}} \right)\mathit{\boldsymbol{f}},j = i;}\\ {\frac{{{E_i}}}{{l_i^2}}\mathit{\boldsymbol{b}}_{iE}^{\rm{T}}\left( { - {t_i}{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{K}}_j}{\mathit{\boldsymbol{K}}^{ - 1}}} \right)\mathit{\boldsymbol{f}},j \ne i.} \end{array}} \right. $ |
这里构造线性近似矩阵函数
优化问题(3)中有时还需考虑一些常规的标量约束gi(x)≤0,如杆件应力、节点位移等.类似半定约束情况,可将约束函数gi(x)近似为x的线性、双线性或多项式函数
| $ {\mathit{\boldsymbol{G}}_j}\left( \mathit{\boldsymbol{x}} \right) = {\rm diag} \left\{ { - {g_1}\left( \mathit{\boldsymbol{x}} \right), - {g_2}\left( \mathit{\boldsymbol{x}} \right), \cdots , - {g_l}\left( \mathit{\boldsymbol{x}} \right)} \right\} \underline \succ \mathit{\boldsymbol{O}}. $ |
下面给出应力约束线性近似函数的半定表达式.应力约束的一般形式为σ ≤ σ ≤ σ,其中σ为杆件应力组成的m维列向量,杆件i的应力为σi(t)=qili/ti=Ei biETK (t)-1f/li,σ、σ分别为同维度的应力上、下限列向量.在设计点t0附近,应力一阶近似函数的向量形式为
| $ \mathit{\boldsymbol{\tilde \sigma }}(\mathit{\boldsymbol{t}}) = \mathit{\boldsymbol{\sigma }}\left( {{\mathit{\boldsymbol{t}}_0}} \right) + \frac{{\partial \mathit{\boldsymbol{\sigma }}}}{{\partial \mathit{\boldsymbol{t}}}}\left| {_{t = {t_0}}} \right.\left( {\mathit{\boldsymbol{t}} - {\mathit{\boldsymbol{t}}_0}} \right), $ |
其中应力的一阶导数为
| $ \partial {\mathit{\boldsymbol{\sigma }}_i}/\partial {t_j} = - {E_i}\mathit{\boldsymbol{b}}_{iE}^{\text{T}}{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{K}}_j}{\mathit{\boldsymbol{K}}^{ - 1}}\mathit{\boldsymbol{f}}/{l_i}. $ |
应力上限半定约束记作Xσ =diag{ σ - σ }
| $ {{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma }} = {\rm diag}\left\{ {\mathit{\boldsymbol{\bar \sigma }} - \mathit{\boldsymbol{\tilde \sigma }}} \right\} = {{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma ,0}} + \sum\limits_{i = 1}^m {{t_i}{{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma ,i}}} , $ |
式中的常值矩阵和系数矩阵分别为:
| $ {{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma ,0}} = {\text{diag}}\left\{ {\mathit{\boldsymbol{\bar \sigma }} - \mathit{\boldsymbol{\sigma }}\left( {{\mathit{\boldsymbol{t}}_0}} \right) + \frac{{\partial \mathit{\boldsymbol{\sigma }}}}{{\partial \mathit{\boldsymbol{t}}}}\left| {_{\mathit{\boldsymbol{t}} = {\mathit{\boldsymbol{t}}_0}}} \right.{\mathit{\boldsymbol{t}}_0}} \right\}, $ |
| $ \mathit{\boldsymbol{\tilde X}}_{\sigma ,i}^ - = {\rm diag}\left\{ { - {{\left. {\frac{{\partial {\sigma _i}}}{{\partial \mathit{\boldsymbol{t}}}}} \right|}_{\mathit{\boldsymbol{t}} = {\mathit{\boldsymbol{t}}_0}}}} \right\}. $ |
同理,应力下限半定约束Xσ =diag{ σ - σ }
| $ {{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma }} = {\rm diag}\left\{ {\mathit{\boldsymbol{\tilde \sigma }} - \mathit{\boldsymbol{\underline \sigma }} } \right\} = {{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma ,0}} + \sum\limits_{i = 1}^m {{t_i}{{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma ,i}}} , $ |
其中常值矩阵和系数矩阵分别为:
| $ {{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma ,0}} = {\rm diag}\left\{ {\mathit{\boldsymbol{\sigma }}\left( {{\mathit{\boldsymbol{t}}_0}} \right) - \mathit{\boldsymbol{\underline \sigma }} - {{\left. {\frac{{\partial \mathit{\boldsymbol{\sigma }}}}{{\partial \mathit{\boldsymbol{t}}}}} \right|}_{\mathit{\boldsymbol{t}} = {\mathit{\boldsymbol{t}}_0}}}{\mathit{\boldsymbol{t}}_0}} \right\}, $ |
| $ {{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma ,i}} = {\rm diag}\left\{ {{{\left. {\frac{{\partial {\mathit{\boldsymbol{\sigma }}_i}}}{{\partial \mathit{\boldsymbol{t}}}}} \right|}_{\mathit{\boldsymbol{t}} = {\mathit{\boldsymbol{t}}_0}}}} \right\}. $ |
对复杂非线性约束进行近似处理后,即可将优化问题(3)表述为仅包含半定约束的近似优化模型:
| $ \left\{ {\begin{array}{*{20}{l}} {\min }&{\eta ,} \\ {{\text{s}}.\;{\text{t}}.}&{{{\mathit{\boldsymbol{\tilde G}}}_j}\left( \mathit{\boldsymbol{x}} \right) \underline \succ \mathit{\boldsymbol{O}},j \in \mathit{\boldsymbol{\tilde J}}.} \end{array}} \right. $ | (10) |
以考虑柔度、基频、全局稳定和应力约束的体积最小化问题为例,近似模型的具体表达式为
| $ \left\{ \begin{gathered} \mathop {\min }\limits_{\mathit{\boldsymbol{t}} \in {{\bf{R}}^m},\mathit{\boldsymbol{v}} \in {\bf{R}}} \mathit{\boldsymbol{v}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\ {\text{s}}.\;{\text{t}}.\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\bar C}&{{\mathit{\boldsymbol{f}}^{\text{T}}}} \\ \mathit{\boldsymbol{f}}&{\mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{t}} \right)} \end{array}} \right] \underline \succ \mathit{\boldsymbol{O}}, \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{t}} \right) - \underline \lambda \left( {{\mathit{\boldsymbol{M}}_{\text{s}}}\left( \mathit{\boldsymbol{t}} \right) + {\mathit{\boldsymbol{M}}_0}} \right) \underline \succ \mathit{\boldsymbol{O}}, \\ \;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde X}}}_{\text{G}}}\left( {\mathit{\boldsymbol{f}},\mathit{\boldsymbol{t}}} \right) = {{\mathit{\boldsymbol{\tilde X}}}_{{\text{G}},0}} + \sum\limits_{i = 1}^m {{t_i}{{\mathit{\boldsymbol{\tilde X}}}_{{\text{G}},i}}} \underline \succ \mathit{\boldsymbol{O}}, \\ \;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma }} = {{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma ,0}} + \sum\limits_{i = 1}^m {{t_i}{{\mathit{\boldsymbol{\tilde X}}}_{\bar \sigma ,i}}} \underline \succ \mathit{\boldsymbol{O}}, \\ \;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma }} = {{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma ,0}} + \sum\limits_{i = 1}^m {{t_i}{{\mathit{\boldsymbol{\tilde X}}}_{\underline \sigma ,i}}} \underline \succ \mathit{\boldsymbol{O}}, \\ \;\;\;\;\;\;\;\;\;\; - \sum\limits_{i = 1}^m {{t_i}} + v \geqslant 0, \\ \;\;\;\;\;\;\;\;\;\;{\text{diag}}\left\{ {\mathit{\boldsymbol{\bar t}} - \mathit{\boldsymbol{t}}} \right\} \underline \succ \mathit{\boldsymbol{O}}, \\ \;\;\;\;\;\;\;\;\;\;{\text{diag}}\left\{ {\mathit{\boldsymbol{t}} - \mathit{\boldsymbol{\underline t}} } \right\} \underline \succ \mathit{\boldsymbol{O}}. \\ \end{gathered} \right. $ | (11) |
式中t、t分别为近似问题中变量t的上、下限,可通过一些常用的运动极限策略给定.
模型(11)是一个线性半定规划问题,参照对模型(8)的处理方式将其转化为标准形式(7),其中的变量和系数的具体表达式见表 3.
| 表 3 线性近似半定规划模型中的变量和系数 Tab. 3 Variables and coefficients in linear approximate semidefinite programming model |
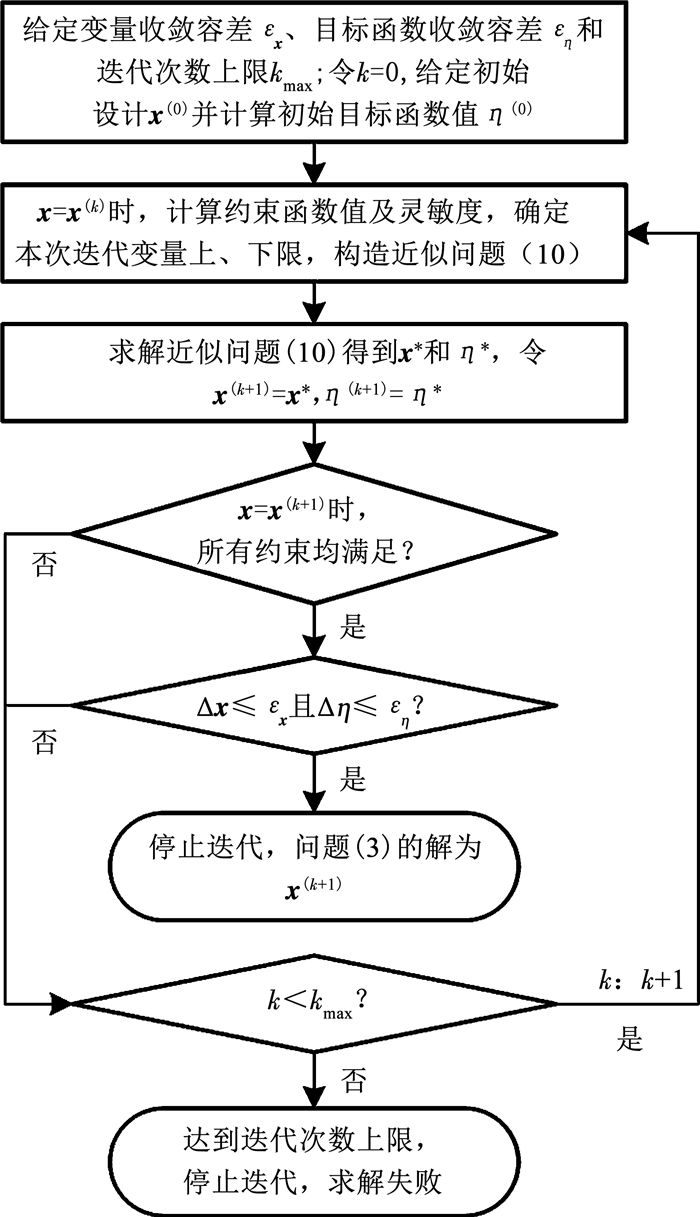
求解优化问题(3)时,若存在非线性约束函数,则可基于近似模型(10)进行迭代求解,算法如下.
给定初始设计x(0),其对应的目标函数值为η(0);给定变量收敛容差εx,目标收敛容差εη;给定迭代次数上限kmax.令k=0.
Step 1 构造近似问题. x=x (k)时,根据约束函数的函数值和灵敏度度信息计算各个
Step 2 变量更新.求解近似问题(10),所得解为x*和η*,令x(k+1)=x*,η(k+1)=η*.
Step 3 约束满足情况判定. x=x (k+1)时,进行必要的计算以判定原问题(3)各约束的满足情况.若优化约束全部满足,则进入step4,否则进入step5.
Step 4 迭代收敛情况判定.计算Δx=‖ (x(k+1)-x(k)) /x(k)‖和Δη= (η(k+1)-η(k)) /η(k).若Δx≤εx且Δη≤εη,则停止迭代,问题(3)的解为x(k+1);否则进入step5.
Step 5 迭代次数更新.若k < kmax,k:=k+1,回到step1;否则停止迭代.
上述算法流程图如图 1所示.
|
图 1 非线性半定规划序列近似求解算法流程 Fig. 1 Flow chart of the sequential approximate algorithm for nonlinear SDP problems |
本文求解若干桁架结构优化问题,以验证给出的半定规划模型的正确性和求解算法的有效性.基结构中各杆均为实心圆截面杆,各算例如图 2所示的直线表示杆件,直线粗细表示杆件相对直径的大小.实心圆圈表示固定节点,位置不变;空心圆圈表示自由节点,位置可变.箭头表示外部载荷.
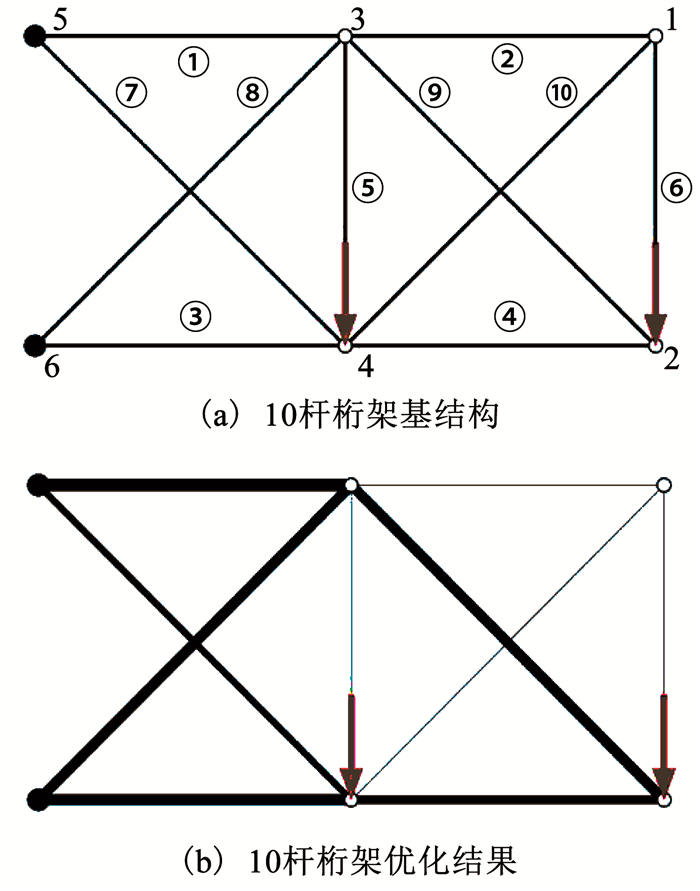
|
图 2 10杆桁架算例 Fig. 2 The 10-bar truss example |
图 2(a)所示的10杆桁架结构,共有6个节点,横向和纵向相邻节点间距均为9.144 m,节点2、4分别作用竖直向下,幅值为4.448 222×105N的集中载荷.各杆的许用应力均为±172.368 947 MPa,所有自由节点的纵向允许位移均为±50.8 mm.材料弹性模量为68.947 579 GPa,密度为2.767 990×103 kg/m3.各杆横截面积下限均为6.451 6×10-5 m2,初始设计均为6.451 6×10-3 m2.该算例取自文献[28].
考虑应力和位移约束下的体积最小化问题,需使用非线性半定规划模型描述.参照应力约束的处理方式对位移约束进行处理.根据经验,位移约束取2阶近似时可得到较好的优化结果,求解时调用PENLAB即可.为加快收敛,在迭代过程中使用了与移动渐近线方法(可见文献[29])类似的变量上、下限更新策略.优化结果如图 2(b)所示.
对该例,不同文献给出的最优结构质量从2 298.343 5 kg(文献[30])到2 318.764 2 kg不等(见文献[28]对比).由表 4可见,本文优化结果与文献[30]给出的结果仅存在微小差异,在均满足优化约束的情况下,本文优化结果的结构质量比文献[30]略小,且分析迭代次数略少.本例简单验证了本文模型和算法的正确性以及数值求解的精度.
| 表 4 10杆桁架优化结果对比 Tab. 4 Comparison of optimization results for the 10-bar truss |
图 3(a)所示的5×3×3三维桁架基结构,共有45个节点和632根互不重叠的杆件.节点均匀分布,沿3个方向相邻节点的间隔均为1 m,且每根杆件沿各方向的投影均不超过2 m.最左侧9个节点固定,最右侧中间节点作用如图所示幅值为9 800 N的集中载荷.各杆初始直径均为40 mm.材料弹性模量为210 GPa,密度为7 900 kg/m3.该算例取自文献[17].
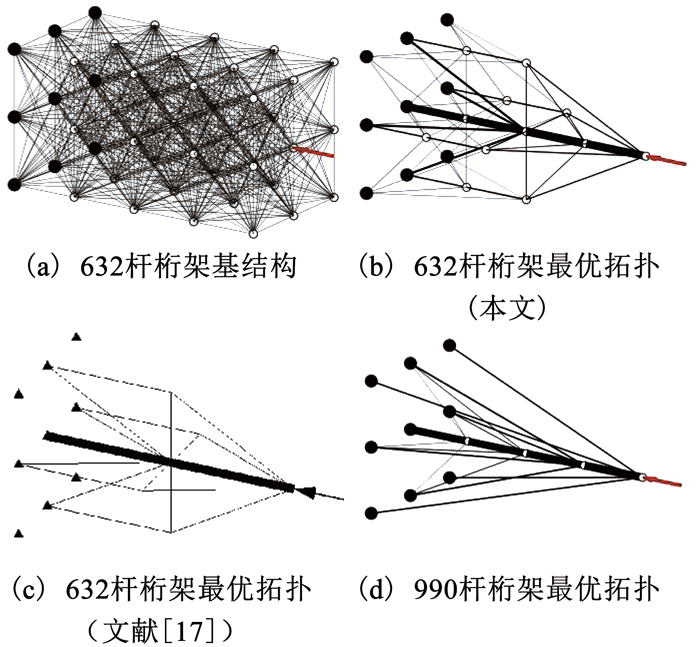
|
图 3 5×3×3桁架算例 Fig. 3 The 5×3×3 truss example |
考虑柔度和基频约束下的体积最小化问题,可使用线性半定规划模型描述.参照文献[17]将柔度上限取为0.026 J(注意:由于柔度定义不同,该值与文献[17]存在2倍关系),基频下限取为41 Hz.使用SeDuMi或SDPT3求解得到的结果相同.将优化结果中横截面积小于1×10-8 m2的杆件删除,得到的最优拓扑如图 3(b)所示.优化前后的结构特性见表 5.
| 表 5 5×3×3桁架结构拓扑优化特性对比 Tab. 5 Property comparison of the 5×3×3 truss topology optimization |
基结构各杆横截面积相同,柔度和基频约束均不满足;最优拓扑仅保留了56根杆件,以初始体积的20.69%满足了全部约束.相比文献[17]的最优拓扑(图 3(c),特性见表 5),本文所得最优拓扑保留的杆件较多,但满足全部约束所需的材料体积却比文献[17]减少了37.89 %.实际上,文献[17]删除细杆后的最优拓扑已经出现机构,其基频为0.可见,本文得到的优化结果更轻,且在几何上是稳定的.
由于基结构中各杆互不重叠且最大杆长受限,图 3(b)所示结果中包含大量短杆.若考虑节点间所有可能的杆件连接情况,基结构中将包含990根杆件,在相同设定下求解得到图 3(d)所示最优拓扑,其特性见表 5.此时优化问题在更大的可行域内寻优,所得最优拓扑的体积更小,杆件也可能更少.
另外,本例基结构和最优拓扑均具有多重基频,说明本文半定模型能够有效处理多重特征值问题.
5.3 算例3——全局稳定约束图 4(a)所示的L型桁架基结构由6个1×1×1的立方体组成,包含28个节点和132根杆件.结构竖直段顶部的4个节点固支,水平段端部上方的两个角点分别作用竖直向下,幅值为0.001的集中载荷.所有杆件的总体积为1,每根杆件的体积均相等.材料弹性模量和密度均取1.该算例取自文献[19].
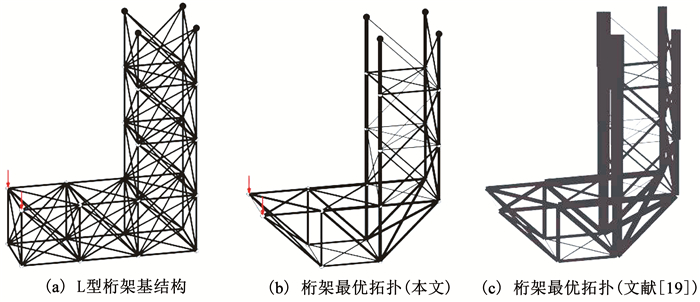
|
图 4 L型桁架算例 Fig. 4 The L-shaped truss example |
考虑柔度和全局稳定约束下的体积最小化问题,使用非线性半定规划模型描述.参照文献[19]将柔度上限取为0.008,临界屈曲载荷因子下限取为1.使用SDPT3进行求解,12次迭代后算法收敛.去除细杆后得到的最优拓扑如图 4(b)所示,图 4(c)为文献[19]的最优拓扑(注意,各图中杆件粗细仅表示相对大小,不代表绝对数值,文献[19]与本文使用的绘制比例不同).结构特性对比见表 6.
| 表 6 L型桁架结构拓扑优化特性对比 Tab. 6 Property comparison of the L-shaped truss topology optimization |
文献[19]将优化问题建模为一个非凸半定规划问题,并使用广义原内点法进行求解;本文则通过杆件内力函数的线性近似将全局稳定约束近似为凸的线性半定规划问题,可以基于线性半定规划求解器进行迭代求解.由表 6可见,两种方法所得最优拓扑的结构特性是一致的.另外,最优拓扑临界屈曲载荷因子的重数为2,说明本文模型和算法能够处理包含多重特征值的全局稳定约束优化问题.
5.4 算例4——混合约束图 5(a)所示的3×3平面桁架基结构,沿各方向跨度均为1,共有9个节点和18根互不重叠的杆件.最左侧3个节点固定,最右侧中间节点处作用水平向左、幅值为1的集中载荷.材料弹性模量为1,密度为1.相关物理量经适当缩放,无需给出具体单位.基结构各杆体积均为5,结构特性见表 7.
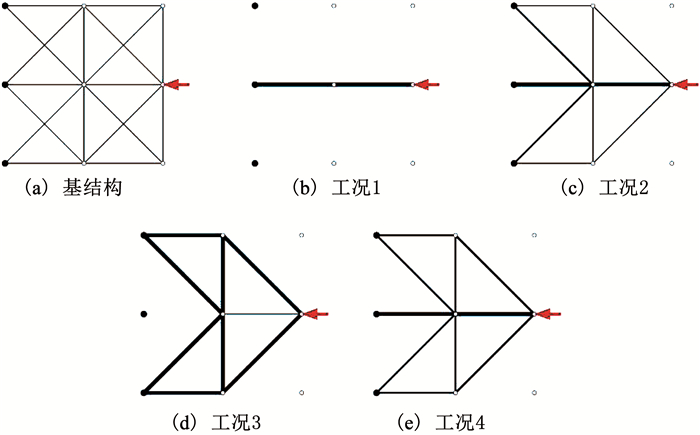
|
图 5 3×3桁架算例基结构及不同工况下的最优拓扑 Fig. 5 The 3×3 truss example, ground structure, and optimal topologies in different cases |
| 表 7 3×3桁架结构拓扑优化特性对比 Tab. 7 Property comparison of the 3×3 truss topology optimization |
考虑体积最小化问题.为对比不同约束下的优化结果,设置如下4个工况:工况1考虑柔度约束;工况2考虑柔度和基频约束;工况3考虑柔度、基频和全局稳定约束;工况4考虑柔度、基频、全局稳定和应力约束.涉及到相关约束时,柔度上限取1,基频下限取0.063 5,临界屈曲载荷因子取1,拉压应力上限均取0.1.前两个工况下的体积最小化问题可建模为线性半定规划;后两个工况包含非线性约束,对应问题可建模为非线性半定规划,需迭代求解.将小于优化结果中最大横截面积0.1%的细杆删除,得到的最优拓扑分别如图 5(b)~图 5(e)所示,其结构特性见表 7.
工况1最优拓扑如图 5(b)所示,该2杆拓扑满足柔度约束,但其构型几何可变,基频为0,不能正常承载.工况2最优拓扑如图 5(c)所示,为进一步满足基频约束,该构型的体积增加到1.414 4,新增的杆件也确保了结构几何不变;但该构型的临界屈曲载荷因子小于1,载荷作用下并非全局稳定.工况3最优拓扑如图 5(d)所示,为进一步满足全局稳定约束,该构型体积增加到8.177 7,拓扑形式相比工况2也有不同;但该构型不满足应力约束.工况4最优拓扑如图 5(e)所示,为进一步满足应力约束,该构型的体积增加到17.500 9,最优拓扑与工况2类似,但各杆横截面积的分布差别很大.
对比可见,考虑不同约束所得最优拓扑存在较大差异.对本例,约束考虑不全面时,优化结果可能体积较小,但未被考虑的约束可能并不满足.此时若以未考虑的约束进行校验,则优化结果不可用.因此,优化模型和算法处理多种约束的能力十分重要.
6 结论1) 基于多种常规约束的等价半定形式或近似半定形式,桁架结构拓扑优化问题可以建模为统一的(近似)半定规划模型.附加变量的引入既简化了目标函数,又使不同目标函数的优化问题具有相对统一的表达式.通过调用已有的半定规划求解器,可处理多种约束下的桁架结构拓扑优化问题.
2) 考虑柔度和基频约束时,半定规划模型使优化问题由非线性非凸变为线性的凸问题.线性半定规划能够高效求解此类问题,所得解即为全局最优解.同时,基频约束的线性半定形式和全局稳定约束的近似线性半定形式有利于避免多重特征值灵敏度分析的困难.
3) 工程结构优化问题的建模求解应谨慎选取设计约束.约束考虑不全面时,优化结果可能并不能满足那些未被考虑的约束.但约束越多,优化问题求解通常就越困难.在对优化问题特性有深入认识的前提下,设计师可对约束进行合理取舍,否则建议尽可能全面地考虑设计约束.
4) 目前的半定规划求解器对连续变量线性半定规划问题的求解较为高效和可靠,因此本文使用基于尺寸优化的拓扑优化策略,即通过将优化结果中的细杆进行过滤得到最优拓扑.
| [1] |
PAN Jin, WANG Deyu. Topology optimization of truss structure with fundamental frequency and frequency domain dynamic response constraints[J]. Acta Mechanica Solida Sinica, 2006, 19(3): 231. DOI:10.1007/s10338-006-0628-2 |
| [2] |
刘晓峰, 阎军, 程耿东. 采用自动分组遗传算法的频率约束下桁架拓扑优化[J]. 计算力学学报, 2011, 28(1): 1. LIU Xiaofeng, YAN Jun, CHENG Gengdong. Topology optimization of skeletal structures with frequency constraints based on automatic grouping genetic algorithm[J]. Chinese Journal of Computational Mechanics, 2011, 28(1): 1. DOI:10.7511/jslx201101001 |
| [3] |
KAVEH A, GHAZAAN M I. Hybridized optimization algorithms for design of trusses with multiple natural frequency constraints[J]. Advances in Engineering Software, 2015, 79: 137. DOI:10.1016/j.advengsoft.2014.10.001 |
| [4] |
HASANÇEBI O, ÇARBAŞ S, DOǦAN E, et al. Performance evaluation of metaheuristic search techniques in the optimum design of real size pin jointed structures[J]. Computers & Structures, 2009, 87(5/6): 284. DOI:10.1016/j.compstruc.2009.01.002 |
| [5] |
SAVSANI V J, TEJANI G G, PATEL V K, et al. Modified meta-heuristics using random mutation for truss topology optimization with static and dynamic constraints[J]. Journal of Computational Design and Engineering, 2017, 4(2): 106. DOI:10.1016/j.jcde.2016.10.002 |
| [6] |
修乃华, 罗自炎. 半定规划[M]. 北京: 北京交通大学出版社, 2014: 1. XIU Naihua, LUO Ziyan. Semidefinite programming[M]. Beijing: Beijing Jiaotong University Press, 2014: 1. |
| [7] |
POTRA F A, WRIGHT S J. Interior-point methods[J]. Journal of Computational and Applied Mathematics, 2000, 124(1/2): 281. DOI:10.1016/s0377-0427(00)00433-7 |
| [8] |
VANDENBERGHE L, BOYD S. Semidefinite programming[J]. SIAM Review, 1996, 38(1): 49. DOI:10.1137/1038003 |
| [9] |
WOLKOWICZ H, SAIGAL R, VANDENBERGHE L. Handbook of semidefinite programming: Theory, algorithms, and applications[M]. Boston/Dordrecht/London: Kluwer Academic Publishers, 2000: 2. DOI:10.1007/978-1-4615-4381-7
|
| [10] |
BOYD S, VANDENBERGHE L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004: 167.
|
| [11] |
YAMASHITA H, YABE H. A survey of numerical methods for nonlinear semidefinite programming[J]. Journal of the Operations Research Society of Japan, 2015, 58(1): 24. DOI:10.15807/jorsj.58.24 |
| [12] |
BEN-TAL A, NEMIROVSKI A. Robust truss topology design via semidefinite programming[J]. SIAM Journal on Optimization, 1997, 7(4): 991. DOI:10.1137/s1052623495291951 |
| [13] |
张家凡, 游蓉. 线性矩阵不等式及其在结构优化设计中的应用[J]. 机械设计, 2002, 19(7): 60. ZHANG Jiafan, YOU Rong. Linear matrix inequalities and its application in structural optimal design[J]. Journal of Machine Design, 2002, 19(7): 60. DOI:10.3969/j.issn.1001-2354.2002.07.021 |
| [14] |
OHSAKI M, FUJISAWA K, KATOH N, et al. Semi-definite programming for topology optimization of trusses under multiple eigenvalue constraints[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 180(1/2): 203. DOI:10.1016/s0045-7825(99)00056-0 |
| [15] |
ACHTZIGER W, KOČVARA M. On the maximization of the fundamental eigenvalue in topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 34(3): 181. DOI:10.1007/s00158-007-0117-3 |
| [16] |
李东泽, 于登云, 马兴瑞. 航天器桁架结构拓扑优化设计[J]. 中国空间科学技术, 2009, 29(4): 1. LI Dongze, YU Dengyun, MA Xingrui. Application of truss topology optimization in spacecraft structures engineering[J]. Chinese Space Science and Technology, 2009, 29(4): 1. DOI:10.3321/j.issn:1000-758X.2009.04.001 |
| [17] |
李东泽, 于登云, 马兴瑞. 基频约束下的桁架结构半定规划法拓扑优化[J]. 工程力学, 2011, 28(2): 181. LI Dongze, YU Dengyun, MA Xingrui. Truss topology optimization with fundamental frequency constraints via semi-definite programming[J]. Engineering Mechanics, 2011, 28(2): 181. |
| [18] |
BEN-TAL A, JARRE F, KOČVARA M, et al. Optimal design of trusses under a nonconvex global buckling constraint[J]. Optimization and Engineering, 2000, 1(2): 189. DOI:10.1023/A:1010091831812 |
| [19] |
KOČVARA M. On the modelling and solving of the truss design problem with global stability constraints[J]. Structural and Multidisciplinary Optimization, 2002, 23(3): 189. DOI:10.1007/s00158-002-0177-3 |
| [20] |
NI Changhui, YAN Jun, CHENG Gengdong, et al. Integrated size and topology optimization of skeletal structures with exact frequency constraints[J]. Structural and Multidisciplinary Optimization, 2014, 50(1): 113. DOI:10.1007/s00158-013-1035-1 |
| [21] |
YAMADA S, KANNO Y. Relaxation approach to topology optimization of frame structure under frequency constraint[J]. Structural and Multidisciplinary Optimization, 2016, 53(4): 731. DOI:10.1007/s00158-015-1353-6 |
| [22] |
ROZVANY G I N. A critical review of established methods of structural topology optimization[J]. Structural and Multidisciplinary Optimization, 2009, 37(3): 217. DOI:10.1007/s00158-007-0217-0 |
| [23] |
王勖成. 有限元方法[M]. 北京: 清华大学出版社, 2003: 485. WANG Xucheng. Finite element method[M]. Beijing: Tsinghua University Press, 2003: 485. |
| [24] |
STURM J F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones[J]. Optimization Methods & Software, 1999, 11(1/2/3/4): 625. DOI:10.1080/10556789908805766 |
| [25] |
TÜTÜNCÜ R H, TOH K C, TODD M J. Solving semidefinite-quadratic-linear programs using SDPT3[J]. Mathematical Programming, 2003, 95(2): 189. DOI:10.1007/s10107-002-0347-5 |
| [26] |
FIALA J, KOCVARA M, STINGL M. PENLAB: A MATLAB solver for nonlinear semidefinite optimization[J/OL]. (2013-11-20). http://arxiv.org/abs/1311.5240
|
| [27] |
KANNO Y, OHSAKI M, KATOH N. Sequential semidefinite programming for optimization of framed structures under multimodal buckling constraints[J]. International Journal of Structural Stability and Dynamics, 2001, 1(4): 585. DOI:10.1142/s0219455401000305 |
| [28] |
钱令希. 工程结构优化设计[M]. 北京: 科学出版社, 2011: 52. QIAN Lingxi. Optimum design of engineering structures[M]. Beijing: Science Press, 2011: 52. |
| [29] |
姚寿文, 崔红伟. 机械结构优化设计[M]. 2版. 北京: 北京理工大学出版社, 2018: 55. YAO Shouwen, CUI Hongwei. An introduction to mechanical structural optimization[M]. 2nd ed. Beijing: Beijing Institute of Technology Press, 2018: 55. |
| [30] |
KHAN M R, WILLMERT K D, THORNTON W A. A new optimality criterion method for large scale structures[C]//Proceedings of the 19th Structures, Structural Dynamics and Materials Conference. Bethesda, MD: AIAA, 1978: 47. DOI: 10.2514/6.1978-470
|
 2019, Vol. 51
2019, Vol. 51


