2. 金属矿山高效开采与安全教育部重点实验室(北京科技大学), 北京 100083;
3. 镍钴资源综合利用国家重点实验室(金川集团有限公司), 甘肃 金昌 737100
2. Key Laboratory High-Efficient Mining and Safety of Metal Mines (University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China;
3. State Key Laboratory of Nickel and Cobalt Resources Comprehensive Utilization (Jinchuan Group Co. LTD), Jinchang 737100, Gansu China
利用炼铁后高炉水淬渣(简称矿渣粉)开发低成本矿用充填胶凝材料时, 采用碱和盐的复合化学作用, 可促使其生成充填体抗压强度根本来源物质, AFt和C-S-H凝胶, 达到胶结充填的目的[1-3].目前, 广泛的研究方法是开展激发剂配比适配试验[4-5], 但高炉水淬矿渣属于炼铁副产品, 其性质受炼铁工艺、铁矿石来源等影响, 并不能用恒定的激发剂配比作用于任一矿渣粉[6-8].针对矿渣开发充填胶凝材料, 在试配试验的基础上, 考察其力学性能或其他方面性能, 结合化学分析手段, 如采用化学结合水失重的方法研究激发剂配比, 利用SEM电镜扫描观察其微观结构, 使用物相分析手段研究其水化产物等, 这些方法均不能从化学机理角度描述激发剂与矿渣粉之间的复杂不确定量化关系, 无法达到定量研究激发剂配比的目的[9-11].
文献[12-17]表明, 智能算法具有高鲁棒性、广泛适用性、全局优化等优点, 可结合复杂问题中不确定规律, 进行自组织、自适应、自学习, 为解决复杂问题提供了新途径.文献[18]通过采集环境因子的大量数据样本, 采用遗传规划法建立其与生物因子之间的量化关系, 识别影响生物因子的关键环境因子.文献[19]鉴于边坡系数与影响因素之间的高度非线性和不确定性, 通过采集影响因素数据样本, 采用遗传规划获得边坡影响因素与安全系数之间的非线性函数关系, 准确获取安全系数的预测结果.因此应用智能算法解决复杂问题时, 获取样本数据是关键的一步.文献[20]虽采用智能算法研究了新型充填胶凝材料激发剂配比, 但进行正交试验时激发剂水平研究区间较小, 无法获取激发剂掺量水平在大区间影响下充填胶结体强度的试验数据.综上所述, 为实现河北某铁矿全尾砂胶结充填成本, 获得满足矿山强度要求的充填胶凝材料最优配比, 本文在水化理论研究的基础上, 合理选取激发剂掺量大区间水平, 开展充填体强度均匀试验, 获取具有代表性的样本数据, 结合遗传规划和遗传算法, 探索一种更为快速准确、简单可靠的激发剂配比优化方法, 以期获得满足目标要求的胶凝材料最优配比, 为今后开发低成本充填胶凝材料提供一种新方法.
1 激发剂配比智能优化决策方法 1.1 激发剂配比均匀试验首先采用均匀设计方法开展不同激发剂配比的充填胶结体单轴抗压强度试验, 基于均匀试验因素水平多, 试验次数少的优点, 设计各激发剂材料多水平掺量的充填体单轴抗压强度试验, 获得n组试验不同龄期的单轴抗压强度测量值为
| $ {\mathit{F}_i}{\rm{ = }}\mathit{f}{\rm{(}}\mathit{M}{\rm{, }}\mathit{N}{\rm{, }}\mathit{T}{\rm{), }}\mathit{i}{\rm{ = 1, }}\mathit{n}{\rm{.}} $ |
式中:Fi为充填体抗压强度测量值;M为激发剂种类;N为激发剂掺量水平;T为养护龄期.
1.2 充填体强度影响函数根据激发剂配比均匀试验结果, 以均匀数值设计方案各激发剂材料的掺量为自变量, 以测定的单轴抗压强度值作为因变量进行智能分析, 基于改进后的遗传规划, 采用遗传树分别构建不同龄期充填体强度与激发剂材料掺量之间的函数关系为
| $ F_k^\prime = {g_k}\left( {M_1^c, M_2^c, M_3^c, M_4^c, \cdots , M_n^c} \right), k = 1, n. $ |
式中:F′k为充填体标准条件下养护k龄期的单轴抗压强度, 其中k的单位为d;gk(·)为k龄期单轴抗压强度的函数;Mnc为第n种激发剂材料掺量.
1.3 激发剂配比优化模型1) 优化模型.k龄期的充填体单轴抗压强度同时满足矿山要求强度, 且之和达到最大时, 可认为目标函数达到最优, 因此以构建的k个龄期充填体强度影响函数值之和最大为优化目标, 建立矿用充填胶凝材料激发剂配比优化模型为
| $ \max \sum\limits_{k = 1}^n {F_k^\prime } \left( {M_1^c, M_2^c, M_3^c, M_4^c, \cdots , M_n^c} \right). $ | (1) |
2) 约束条件.根据激发剂掺量的取值范围及矿山对不同龄期充填体强度的要求, 确定激发剂配比优化模型的约束条件为:
| $ M_n^{{\rm{cl}}} \le M_n^c \le M_n^{c2}, F_k^\prime \ge {G_k}. $ | (2) |
式中:Mnc为激发剂材料n的掺量; Mnc1、Mnc2分别为激发剂材料n掺量的下、上限; Gk为目标要求值.
1.4 优化模型求解基于激发剂配比优化目标函数属于高度非线性函数的考虑, 故采用遗传算法对由式(1)、(2)确定的优化模型进行求解, 由此获取k个龄期的轴抗压强度之和达到最大时激发剂材料的掺量, 最终获得满足各龄期抗压强度的充填胶凝材料最优配比.
为进一步阐述该激发剂配比智能优化决策方法, 结合某铁矿全尾砂新型充填胶凝材料激发剂配比的智能优化进行实例分析.在开展不同激发剂掺量的全尾砂胶砂均匀试验基础上, 根据试验结果建立全尾砂胶结体强度影响函数, 确定激发剂掺量及矿山对抗压强度的要求, 建立激发剂配比优化模型, 对该模型进行智能求解, 从而获得铁矿全尾砂新型充填胶凝材料的最优配比.
2 全尾砂胶结体强度影响函数 2.1 激发剂配比均匀试验及结果 2.1.1 试验材料及方法试验材料包括唐龙建材有限公司的“伟胜牌”高性能粒化高炉矿渣粉(简称矿渣粉), 河北银水公司冶金生石灰(简称生石灰), 陡河电厂脱硫石膏(简称石膏), 冀东42.5水泥(简称水泥), 河北某铁矿全尾砂.充填胶凝材料由水泥、生石灰、石膏、矿渣粉按表 1配比而成, 充填骨料为全尾砂, 料浆质量分数为68%(固体在料浆中的质量百分数), 胶凝材料与全尾砂质量比, 即胶砂比为1:10, 采用该料浆配比参数, 参照GB/T 17671—1999《水泥胶砂强度检验方法(ISO法)》规定,制备出胶砂试块进行养护, 成型后脱模, 养护至规定龄期测其单轴抗压强度.
| 表 1 激发剂配比均匀试验结果 Tab. 1 Result of uniform design experiment |
试验方案由DPS3.0数据处理系统产生, 均匀性偏差为0.049 66, 将激发剂材料作为试验因素, 其在胶凝材料中质量占比作为试验水平, 共选取9个水平.确定激发剂掺量水平时, 考虑成本因素, 尽可能多的使用矿渣粉, 采用少量的高成本激发剂.石膏虽属于工业固废, 但其掺量过高时, 对充填体后期强度存在不利影响[21-22], 因此将石膏试验水平确定为10%~18%, 各水平间距为1%, 单一的石膏对矿渣粉的激发作用并不大, 只有在碱性环境中效果明显[23], 必须添加少量生石灰创造碱性水化环境, 故将生石灰水平确定为1%~5%, 间距为0.5%;早期强度低, 是矿渣基新型充填胶凝材料明显特征, 为确保胶砂试块早期绝对凝固, 试验数据全面可靠, 加入少量水泥作为早强剂, 考虑到生石灰碱性强于水泥, 若是生石灰创造的碱性环境满足矿渣粉水化作用, 则水泥的掺量可为0, 最终确定水泥试验水平为0~4%, 间距为0.5%.
2.2 激发剂对充填体强度影响分析表 2为不同龄期充填体单轴抗压强度与激发剂二项式逐步回归方程的相关参数, x1、x2、x3分别为水泥、生石灰、石膏.偏相关系数是度量偏相关程度和方向的指标, 即多元回归分析中, 在消除其他变量影响的情况下, 所计算的两变量之间的相关系数, 数值越大, 精度越高, t检验值是对统计结果可信度的检验, t越大越可信.结果显示, 各激发剂与充填体抗压强度偏相关系数较大, 可信度较高, 对3 d充填体强度的影响大小顺序为生石灰>石膏>水泥, 对7 d抗压强度的影响顺序为石膏>生石灰>水泥, 对28 d抗压强度的影响顺序为石膏>生石灰>水泥.综合以上分析, 生石灰与石膏对充填体强度的影响大于水泥.
| 表 2 充填体单轴抗压强度回归方程的相关参数 Tab. 2 Related parameters of regression equation of compressive strength of filling body |
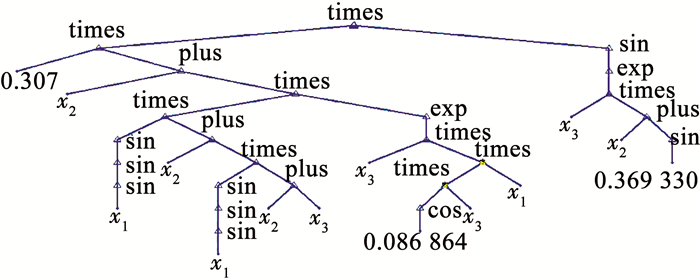
胶凝材料的激发材料配比与全尾砂胶结充填体强度之间具有一种高度非线性关系, 为了能够准确地找到激发剂配比与全尾砂胶结体强度之间的函数关系, 运用Matlab编写程序, 基于改进后的遗传规划建立二者之间的非线性关系.针对全尾砂充填胶凝材料激发剂配比均匀设计试验, 水泥、生石灰、石膏分别在胶凝材料中百分占比作为自变量, 分别用x1、x2、x3表示, 采用遗传规划建立k龄期(k=3、7、28 d)全尾砂充填胶结体强度与水泥、生石灰、石膏三因素在胶凝材料中占比之间的非线性函数关系, 采用遗传规划中的最佳遗传树表征, 由此获得3、7、28 d单轴抗压强度的函数表达式.本文仅给出图 1所示的充填体3 d抗压强度的遗传树结构图, 该龄期的抗压强度函数表达式为
|
图 1 充填体3 d单轴抗压强度遗传树 Fig. 1 Genetic tree for 3 d uniaxial compressive strength of filling body |
| $ \begin{array}{l} F_3^\prime = {\rm{ times }}({\rm{ times }}(0.307, {\rm{ plus }}({x_2}, {\rm{times}}({\rm{times}}\\ (\sin (\sin (\sin ({x_1}))), {\rm{plus }}({x_2}, {\rm{times}}(\sin (\sin (\sin \\ ({x_1}))), {\rm{plus}}({x_2}, {x_3})))), \exp ({\rm{times(}}{x_3}, {\rm{times}}({\rm{times}}\\ ({\rm{cos(}}0.086{\rm{ }}864{\rm{)}}, {x_3}), {x_1})))))), {\rm{sin}}({\rm{exp(times}}\\ ({x_3}, {\rm{plus}}({x_2}, {\rm{sin(}}0.369{\rm{ }}33{\rm{)}}))))). \end{array} $ |
交换变异概率对遗传规划在寻求最优解结构过程中有很大的影响, 采用固定的交换变异概率, 不能反映出不同个体对整体作用影响的大小, 为此编写Matlab计算程序, 实现交换变异概率在计算过程的自适应调整, 依据子代适应度的大小不断调整当前个体交叉变异概率, 使具有较大适应度个体交换变异概率减小, 有助于优良群体积累, 以提高GP收敛速度, 寻求最优解结构.
| $ \begin{array}{l} {P_{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{cl}}}}, {f^\prime } < {f_{{\rm{avg}}}};}\\ {{P_{{\rm{cl}}}} - \frac{{\left( {{P_{{\rm{cl}}}} - {P_{c2}}} \right)\left( {{f^\prime } - {f_{{\rm{avg}}}}} \right)}}{{{f_{{\rm{max}}}}}} - {f_{{\rm{avg}}}}, {f^\prime } \ge {f_{{\rm{avg}}}}.} \end{array}} \right.\\ {P_{\rm{m}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{ml}}}}, f < {f_{{\rm{avg}}}};}\\ {{P_{{\rm{ml}}}} - \frac{{\left( {{P_{{\rm{ml}}}} - {P_{{\rm{m}}2}}} \right)\left( {{f_{{\rm{avg}}}} - f} \right)}}{{{f_{{\rm{max}}}} - {f_{{\rm{avg}}}}}}, f \ge {f_{{\rm{avg}}}}.} \end{array}} \right. \end{array} $ |
式中:Pc、Pm分别为当前个体交换、变异概率; Pc1、Pm1分别为最大交换、变异概率; Pc2、Pm2分别为最小交换变异概率;f′为交换个体较大适应度; f为变异个体适应度; favg为当代种群的平均适应度; fmax为当代种群的最大适应度.
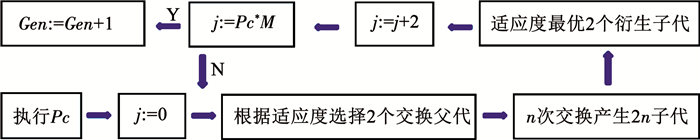
2.4.2 适应度竞争交换方式交换是驱动遗传规划向良好方向进化的主要动力.传统的遗传规划在当前概率将选出的两个个体进行交换, 所产生的两个新个体插入新群体中, 继续进行下一代的遗传操作.虽然子代通过遗传算子继承了父代的遗传基因, 若是两个子代较两个父代更优异, 则GP会具备遗传的稳定性及种群的多样性, 收敛速度也较快;若是子代劣于父代, 这种替代反而会导致种群中的染色体退化.基于“适应度竞争机制”的交换方式, 执行交换概率, 选择交换次数n为4, 运算精度满足要求, 即父代进行4次交换, 产生8个子代, 对比8个子代的适应度, 选择最优的两个子代进入下一代群体繁衍.图 2为采用适应度竞争交换方式的运行过程, 若是交换概率达到适应度函数的要求, 则进行个体加入到新群体进行下一代交换, 若是未达到适应度函数的要求, 则动态调整交换概率, 重新进行本代交换.
|
图 2 适应度竞争交换方式运算过程 Fig. 2 Calculation of the exchange of fitness competition |
图 3(a)、(b)给出3、7 d全尾砂胶结体强度试验值与计算值之间的关系.由此可知, 9组试验中, 相比改进前的遗传规划, 改进后的遗传规划学习计算值与不同龄期的抗压强度试验值比较接近, 误差较小.图 4(a)、(b)为每个进化代数充填体7 d抗压强度期望值, 近似值与激发剂之间的变化关系, 由图 4可知随着进化代数的增加, 期望值逐渐逼近进化的近似值, 当进化达到一定代数时, 充填体强度模型收敛, 达到精度要求, 改进前的遗传规划在96代时精度达到要求, 而交换变异概率及交换算子改进后的遗传规划在49代时满足算法的终止法则, 较改进前的遗传规划, 收敛速度快.因此, 基于动态自适应概率与适应度竞争交换的遗传规划进化学习可有效反映激发剂材料占比与全尾砂新型充填胶凝材料胶结体之间的非线性关系, 建立的函数模型精度较高, 为激发剂配比优化模型的建立奠定基础.

|
图 3 试验值与计算值 Fig. 3 Test value and calculated value |

|
图 4 遗传规划进化过程 Fig. 4 Evolutionary process of genetic programming |
矿山要求充填体3 d抗压强度为0.5 MPa, 7 d抗压强度为1.5 MPa, 28 d抗压强度为3.0 MPa, 将矿山要求强度作为目标函数最低要求值, 基于全尾砂充填胶结体3、7、28 d单轴抗压强度之和最大为优化目标, 由此建立激发剂配比优化模型:
| $ \begin{array}{l} \max \sum\limits_{k = 1}^n {F_k^\prime } \left( {M_1^c, M_2^c, M_3^c, M_4^c, \cdots , M_n^c} \right) = \\ F_3^\prime + F_7^\prime + F_{28}^\prime = 0.309*(((x(2) + (x(2) + x(3)))*\\ \sin (\sin (\sin (x(1)))) = \sin (\sin (\sin (x(1))))*\\ \exp (x(3)*x(1)*x(3)*\cos (0.086864))) + \\ x(2))*\sin (\exp (x(3)*(x(2) + \sin (0.369330)))) + \\ \begin{array}{*{20}{l}} {\sin (x(2)*x(3) + \sin (x(3))*\sin ((\sin (x(3))*}\\ {x(2)*(\sin (x(2)*\sin (x(3))) + x(2) + } \end{array}\\ \begin{array}{*{20}{l}} {\sin (x(3))) + x(2) + \sin (x(3)))*\sin (x(3)) - }\\ {x(2)*x(2)*(x(3) - x(1))) + (\exp (\cos (\exp (x(3))) + }\\ {x(3) - \sin (x(3))*0.678620*\cos (x(1) + x(2) + } \end{array}\\ \begin{array}{*{20}{l}} {x(3)) = \sin (\sin (x(1))))*}\\ {\sin (\sin (\exp (x(2)))*\sin (x(3)*(\exp (x(3)) + }\\ {\sin (x(1)) - \cos (\sin (0.892940)))).} \end{array} \end{array} $ |
考虑到激发剂种类及掺量对充填胶凝材料成本的影响, 水泥和熟料作为激发剂材料成本相对较高, 因此激发剂材料水泥和熟料的占比尽可能低, 由此确定优化模型的约束条件为:
| $ \begin{array}{*{20}{c}} {0 \le {x_1} \le 4, 1 \le {x_2} \le 5, 10 \le {x_3} \le 8, }\\ {F_3^\prime \ge 0.5, F_7^\prime \ge 2.0, F_3^\prime \ge 3.0.} \end{array} $ |
利用遗传算法的全局搜索能力, 求解由本文确定的激发剂配比优化模型.首先设置遗传算法的参数见表 3;然后进行遗传算法操作:即随机产生初始群体→个体适应度评价→选择操作→交叉操作→变异操作→终止法则(最大遗传代数);最终获得满足矿山要求充填体抗压强度所对应的胶凝材料最优配比为:水泥0、生石灰2.91%、石膏17.39%、矿渣粉79.7%.
| 表 3 遗传算法参数 Tab. 3 Genetic algorithm parameters |
根据激发剂配比智能优化方法得到充填胶凝材料优化配比为:水泥0、生石灰2.91%、石膏17.39%、矿渣粉79.7%.为验证智能优化方法获得的激发剂配比对矿渣粉激发作用效果, 利用正交设计安排验证试验.采用上述试验方法, 充填料浆浓度为68%, 胶砂比提高至1:5和1:8, 试验设计采用L9(34)表, 即3水平4因素的正交设计表, 试验方案中前两个因素分别为生石灰、石膏在胶凝材料中的质量占比, 后两个因素为空白列, 正交设计试验见表 4.图 5(a)、(b)分别为胶砂比1:5和1:8时充填体抗压强度与激发剂材料关系曲线, 由此可获得以下结论:
| 表 4 正交设计的试验因素与水平 Tab. 4 Experimental factors and levels of orthogonal design |

|
图 5 胶结体强度验证试验结果 Fig. 5 Verification test results of cement strength verification |
1) 胶砂比1:5或者1:8时, 7、28 d抗压强度最高分别为2.82、1.77 MPa, 28 d抗压强度分别为5.97、3.38 MPa, 此时胶凝材料的配比为生石灰3.0%、石膏17%、矿渣粉80%, 与激发剂配比优化方法确定的胶凝材料最优配比(生石灰2.91%、石膏17.39%、矿渣粉79.7%)吻合.
2) 相同龄期条件下, 验证试验的各组试验强度值相差不大, 结果较为平均, 这是因为各组激发剂配比是在优化配比附近, 说明激发剂优化配比附近不仅激发效果好, 而且效果稳定, 这也为矿山新型充填胶凝材料的工业生产提供较好的保障.
3.4 充填胶凝材料成本分析根据市场调研, 河北地区42.5/t水泥出厂价为450元/t左右, 邯郸邢台地区矿渣粉的出厂价格为240元/t, 生石灰为400元/t, 烟气脱硫石膏为80元/t, 若是以生石灰3.0%、石膏17%、矿渣粉80%的配比制备全尾砂充填胶凝材料, 原材料价格为215元/t, 加上生产、运输、销售等费用120元/t, 新型充填胶凝材料的价格低于350元/t, 与42.5水泥相比, 成本可降低22%, 伴随环保压力, 水泥生产受限制, 成本必定逐年增长, 这种绿色高效的新型充填材料可有效降低矿山充填成本, 提高矿山企业经济效益.
4 结论1) 激发剂配比均匀试验结果显示, 对3 d充填体强度的影响大小顺序为生石灰>石膏>水泥, 对7 d抗压强度的影响顺序为石膏>生石灰>水泥, 对28 d抗压强度的影响顺序为石膏>生石灰>水泥.综合结果表明, 生石灰与石膏对充填体强度的影响大于水泥.
2) 采用动态自适应和基于适应度竞争交换方式的遗传规划表征遗传树结构, 建立全尾砂充填体抗压强度与激发剂配比之间的非线性复杂关系, 改进前的遗传规划在96代时精度达到要求, 而改进后的遗传规划在49代满足算法的终止法则, 相比之下, 其收敛速度快, 由此获得的计算值与试验值非常接近, 误差小, 函数精度较高.
3) 应用激发剂配比智能优化决策方法, 获得满足目标要求的胶凝材料优化配比为生石灰2.91%、石膏17.39%、矿渣粉79.7%;验证试验结果显示, 胶凝材料最优配比为生石灰3.0%、石膏17%、矿渣粉80%时, 充填体7、28 d抗压强度达到最大, 与采用激发剂智能优化方法获得的激发剂优化配比吻合.以生石灰3.0%、石膏17%、矿渣粉80%的配比制备全尾砂充填胶凝材料, 相对42.5水泥, 可降低材料成本22%.
| [1] |
杨志强, 高谦, 蔡美峰, 等. 我国大型贫铁矿充填法开采关键技术与发展方向[J]. 矿业工程研究, 2015, 30(1): 38. YANG Zhiqiang, GAO Qian, CAI Meifeng, et al. Key technology and developmental direction of the filling mining for large lean ore deposits in China[J]. Mineral Engineering Research, 2015, 30(1): 38. DOI:10.13582/j.cnki.1674-5876.2015.01.009 |
| [2] |
杨志强, 高谦, 王永前, 等. 利用金川水淬镍渣尾砂开发新型充填胶凝剂试验研究[J]. 岩土工程学报, 2014, 36(8): 1498. YANG Zhiqiang, GAO Qian, WANG Yongqian, et al. Experimental study on new filling cementing material using water-hardening nickel slag tailings of Jinchuan Mine[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1498. DOI:10.11779/CJGE201408016 |
| [3] |
李茂辉, 杨志强, 王有团, 等. 粉煤灰复合胶凝材料充填体强度与水化机理研究[J]. 中国矿业大学学报, 2015, 44(4): 650. LI Maohui, YANG Zhiqiang, WANG Youtuan, et al. Experiment study of compressive strength and mechanical property of filling body for fly ash composite cementitious materials[J]. Journal of China University of Mining & Technology, 2015, 44(4): 650. DOI:10.13247/j.cnki.jcumt.000365 |
| [4] |
王冲, 杨长辉, 钱觉时, 等. 粉煤灰与矿渣的早期火山灰反应放热行为及其机理[J]. 硅酸盐学报, 2012, 40(7): 1050. WANG Chong, YANG Changhui, QIAN Jueshi, et al. Behavior and mechanism of pozzolanic reaction heat of fly ash and ground granulated blastfurnace slag at early age[J]. Journal of the Chinese Ceramic Society, 2012, 40(7): 1050. DOI:10.14062/j.issn.0454-5648.2012.07.007 |
| [5] |
杨云鹏, 高谦. 尾砂新型复合胶结材料实验研究[J]. 岩石力学与工程学报, 2012, 31(s1): 2906. YANG Yunpeng, GAO Qian. Experimental study of a new commenting material using tailings[J]. Chinese Journal of Rock Mechanics & Engineering, 2012, 31(s1): 2906. |
| [6] |
候春华, 杨志强, 高谦, 等. 金川全尾砂棒磨砂新型充填胶凝材料试验研究[J]. 山东科技大学学报(自然科学版), 2015, 34(3): 78. HOU Chunhua, YANG Zhiqiang, GAO Qian, et al. Experimental research on a new filling material compound of whole tailings and rod milling sand in Jinchuan Mine[J]. Journal of Shandong University of Science & Technology, 2015, 34(3): 78. DOI:10.16452/j.cnki.sdkjzk.20150619.013 |
| [7] |
刘仍光, 丁士东, 阎培渝. 水化环境对粒化高炉矿渣粉水化产物性能影响[J]. 硅酸盐通报, 2015, 34(6): 1594. LIU Rengguang, DING Shidong, YAN Peiyu. Influence of hydration environment on the characteristics of ground granulated blast furnace slag hydration products[J]. Bulletin of the Chinese Ceramic Society, 2015, 34(6): 1594. DOI:10.16552/j.cnki.issn1001-1625.2015.06.028 |
| [8] |
王强, 曹丰泽, 米贵东. 矿渣在无化学激发条件下水化产物的特性[J]. 电子显微学报, 2015, 34(6): 459. WANG Qiang, CAO Fengze, MI Guidong. Properties of the hydration products of GGBS without alkali activation[J]. Journal of Chinese Electron Microscopy Society, 2015, 34(6): 459. DOI:10.3969/j.issn.1000-6281.2015.06.002 |
| [9] |
吴蓬, 吕宪俊, 王俊祥, 等. 硬石膏对熟料激发矿渣水化反应的影响[J]. 中国矿业大学学报, 2016, 45(3): 615. WU Peng, LV Xianjun, WANG Junxiang, et al. Effect of anhydrite on hydration of clinker activated slag cementing materials[J]. Journal of China University of Mining & Technology, 2016, 45(3): 615. DOI:10.13247/j.cnki.jcumt.000518 |
| [10] |
王有团, 杨志强, 李茂辉, 等. 全尾砂-棒磨砂新型胶凝充填材料的制备[J]. 材料研究学报, 2015, 29(4): 291. WANG Youtuan, YANG Zhiqiang, LI Maohui, et al. Preparation of new backfill cementitious materials with unclassified tailings-rod milling sands[J]. Chinese Journal of Materials Research, 2015, 29(4): 291. DOI:10.11901/1005.3093.2014.404 |
| [11] |
董璐, 高谦, 南世卿, 等. 超细全尾砂新型胶结充填料水化机理与性能[J]. 中南大学学报(自然科学版), 2013, 44(4): 1571. DONG Lu, GAO Qian, NAN Shiqin, et al. Performance and hydration mechanism of new super fine cemented whole-tailings backfilling materials[J]. Journal of Central South University (Science and Technology), 2013, 44(4): 1571. |
| [12] |
秦国华, 王子琨, 吴竹溪, 等. 基于表面网格离散化与遗传算法的复杂工件装夹布局规划方法[J]. 机械工程学报, 2016, 52(13): 195. QIN Guohua, WANG Zikun, WU Zhuxi, et al. A planning method of fixturing layout for complex workpieces based on surface discretization and genetic algorithm[J]. Journal of Mechanical Engineering, 2016, 52(13): 195. DOI:10.3901/JME.2016.13.195 |
| [13] |
BANZHAF W, FRANCONE F D, NORDIN P. The effect of extensive use of the mutation operator on generalization in genetic programming using sparse data sets[C]//International Conference on Parallel Problem Solving From Nature. Berlin, Heidelberg: Springer-Verlag, 1996: 300. DOI: 10.1007/3-540-61723-x_994
|
| [14] |
PEREIRA M D A, JUNIOR C A D, VASCONCELOS J A D. A niched genetic programming algorithm for classification rules discovery in geographic databases[J]. Lecture Notes in Computer Science, 2010, 6457: 260. DOI:10.1007/978-3-642-17298-4_27 |
| [15] |
GUVEN A, AZAMATHULLA H M, ZAKARIA N A. Linear genetic programming for prediction of circular pile scour[J]. Ocean Engineering, 2009, 36(12/13): 985. DOI:10.1016/j.oceaneng.2009.05.010 |
| [16] |
GARG P. A comparison between memetic algorithm and genetic algorithm for the cryptanalysis of simplified data encryption standard algorithm[J]. International Journal of Network Security & Its Applications, 2009, 1(1): 34. |
| [17] |
DORRONSORO B, BOUVRY P. Adaptive neighborhoods for cellular genetic algorithms[C]//Proceedings of the IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum. Shanghai: IEEE, 2011: 388. DOI: 10.1109/IPDPS.2011.168
|
| [18] |
王俊娜, 李翀, 段辛斌, 等. 基于遗传规划法识别影响鱼类丰度的关键环境因子[J]. 水利学报, 2012, 43(7): 860. WANG Junna, LI Chong, DUAN Xinbin, et al. Identification of significant environmental factors affecting fish abundance by genetic programming[J]. Journal of Hydraulic Engineering, 2012, 43(7): 860. DOI:10.13243/j.cnki.slxb.2012.07.006 |
| [19] |
翟淑花, 吴爱祥, 高谦, 等. 基于RS-GP模型的边坡安全系数预测[J]. 北京科技大学学报, 2011, 33(1): 6. ZHAI Shuhua, WU Aixiang, GAO Qian, et al. Prediction of slope safety factor based on the RS-GP model[J]. Journal of University of Science & Technology Beijing, 2011, 33(1): 6. DOI:10.13374/j.issn1001-053x.2011.01.019 |
| [20] |
李茂辉, 陈志杰, 高谦. 基于棒磨砂充填料的新型充填胶凝材料优化决策[J]. 金属矿山, 2018(2): 64. LI Maohui, CHEN Zhijie, GAO Qian. Optimized decision for the development of new backfill cementing materials based on the rod milling sand[J]. Metal Mine, 2018(2): 64. DOI:10.19614/j.cnki.jsks.201802012 |
| [21] |
李少辉.补加石膏对水泥矿渣粉复合胶凝材料性能的影响[D].西安: 西安建筑科技大学, 2010 LI Shaohui. Influences of complement gypsum on the performances of cement-slag binder[D]. Xi'an: Xi'an University of Architecture and Technology, 2010. DOI: 10.7666/d.d192276 http://xueshu.baidu.com/usercenter/paper/show?paperid=2185fcb9daaaed7205c6e5fdc98cab8a&site=xueshu_se&hitarticle=1 |
| [22] |
薛改利, 杨志强, 高谦, 等. 全尾砂新型充填胶凝材料在南洺河铁矿的应用[J]. 有色金属(矿山部分), 2014, 66(6): 66. XUE Gaili, YANG Zhiqiang, GAO Qian, et al. Application of new filling cementing material based on tailings in Nanminghe Iron Mine[J]. Nonferrous Metals (Mine Section), 2014, 66(6): 66. DOI:10.3969/j.issn.1671-4172.2014.06.015 |
| [23] |
黎良元, 石宗利, 艾永平. 石膏-矿渣胶凝材料的碱性激发作用[J]. 硅酸盐学报, 2008, 36(3): 405. LI Liangyuan, SHI Zongli, AI Yongping. Alkaline activation of gypsum-granulated blast furnace slag cementing materials[J]. Journal of the Chinese Ceramic Society, 2008, 36(3): 405. DOI:10.14062/j.issn.0454-5648.2008.03.004 |
 2019, Vol. 51
2019, Vol. 51


