2. 中国科学院大学, 北京 100149
2. University of Chinese Academy of Sciences, Beijing 100149, China
TEC作为一种常用的制冷方式, 因其无振动、无噪声、寿命长、不需制冷剂、易安装等优点在CCD制冷、精密温控等领域有着广泛的应用[1].通常, 用户可从厂家选购到1~5级的TEC, 并参考厂家提供的性能曲线来判断所选择的TEC是否满足要求.但厂家提供的性能曲线通常是虚高的, 且误差随TEC级数增加而增大.例如, 对于本文中所分析的5级TEC, 热端为300 K时, 按厂家参数, 空气中最低能制冷到165.0 K, 而实际上, 即使在真空中最低也仅能制冷到182.0 K, 在空气中仅能达到196.0 K, 误差达31 K, 这根本无法达到厂家所声称的性能.因此, 在选购时有必要对TEC性能进行评估以确保所选择的TEC能够满足要求, 很多文献对TEC性能的计算和优化模型进行了研究[2-4], 但计算中所用的热电材料参数仅有极少数厂家会提供[5], 故而仅有少数文献对其模型进行了实验验证.
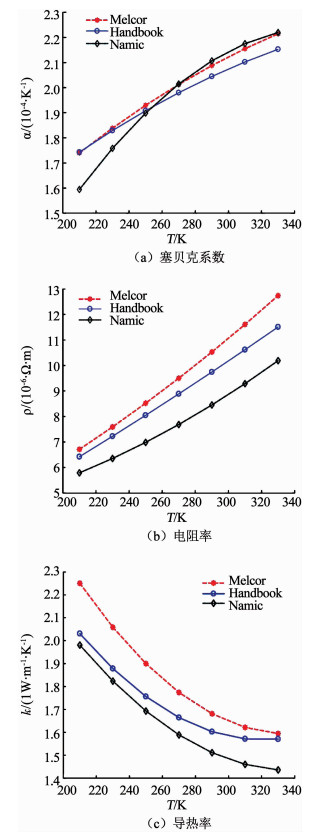
文献[6]中计算TEC性能时即是采用的厂家20余年前的材料参数;文献[5]则是通过相关文献提供的Melcor公司的材料参数对上海彭浦制冷厂的TEC进行计算.实际上, 从图 2可看出, 不同厂家热电材料参数有着一定差别, 并不能通用, 而随着材料的更新换代, 旧的材料参数也将引起一定的误差, 故而文献[5-6]中验证其计算模型准确度的结论缺乏说服力;文献[7]通过Melcor公司提供的参数对该厂家TEC性能进行了计算和实验验证, 但提供材料参数的厂家终归是极少数.因此, 可有效表征热电材料性能的参数的提取对于TEC性能的评估变得至关重要.
|
图 2 材料参数随温度的变化关系 Fig. 2 Material parameters as a function of temperature |
一些研究人员对TEC参数进行了提取, 所提取的参数一类为组件参数, 即整个TEC的塞贝克系数、电阻和热导;另一类为热电材料参数.热电材料参数可通过组件参数和TEC的尺寸计算, 因此, 在知道TEC尺寸时, 两类参数是等同的.而根据所提取的参数是否随温度变化, 所提取的参数又可分为常物性参数和温度依赖的参数.
文献[8-11]利用厂家提供的极值计算了常物性的组件参数, 但热电材料性能是随着温度降低而变差的, 而更高级数TEC有着更低的制冷温度, 因此, 利用极值计算的组件参数对于一、二级TEC计算有着较好效果, 但对于更高级数TEC计算结果并不理想[9].文献[12-13]则通过极值, 考虑进TEC的尺寸后计算了常物性材料参数, 而文献[14]则通过TEC性能曲线中多个工作点计算了常物性组件参数.显然, 这和文献[8-11]所提取的组件参数存在着适用范围受限的缺点.以上文献中, 由于一级TEC工作时最大温差一般 < 70 K, 因此所提取的参数可视为代表热电材料在较高温度(一级TEC的工作温度区间)时的性能, 这对于计算一级TEC所引起的误差是尚可接受的[10, 12-13].而要想使所提取的材料参数适用于任何级数的TEC, 则必须考虑参数随温度的变化.
文献[15]利用厂家提供的软件, 根据基本热电公式, 分别计算了三种材料参数随温度的变化.由于并不知道厂家在计算TEC性能时的计算模型, 因此, 所提取的参数能否应用于其它结构TEC的计算仍有待实验验证, 而且也很少有厂家提供类似的软件, 这就导致该方法的局限性.为降低厂家性能曲线的误差, 文献[16-18]为TEC两端提供一定温差, 根据基本热电公式计算了组件参数, 这种方法可很好地计算热电材料的性能, 文献[19-21]则是通过测量电流瞬时变化时TEC的工作状况来提取模块参数, 将所提取的参数视为冷热端平均温度的函数.以上方法要想获得适用温区大的参数, 就要为TEC提供更低的温度, 这将导致测试装置变得复杂.文献[22]中利用有限元法提取的材料参数已验证完全可取代材料参数实测值进行TEC性能计算, 但计算量相对较大.
综上所述, 除文献[22]外, 目前并没有一种简单实用的方法, 可方便的提取能够有效表征不同温度下热电材料性能的参数.本文提出了一种利用中值法确定电偶臂材料参数, 然后根据基本热电公式和TEC实测工作数据对材料参数进行提取的方法.所提取的材料参数在计算另一款5级TEC时有着较高准确度, 表明所提取的材料参数可有效表征热电材料的性能.
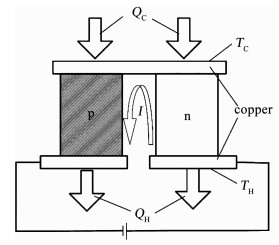
1 TEC性能的计算方法 1.1 TEC性能计算的基本公式如图 1所示, 是一个组成TEC的热电偶对的工作原理.
|
图 1 热电偶模型 Fig. 1 Model of a thermoelectric couple |
电流从pn结中流过时, 电偶对两端节点处会产生吸热和放热现象, 从而形成冷端和热端.在冷端, 根据热电原理基本公式, 所吸收的热量为
| $ {Q_{\rm{C}}} = \alpha I{T_{\rm{C}}} - \frac{1}{2}{I^2}R - K\Delta T - \frac{1}{2}\tau I\Delta T. $ | (1) |
式中:αITC为帕尔帖效应,
则制冷温度和电压分别为
| $ {{T_{\rm{C}}} = \frac{{K{T_{\rm{H}}} + 0.5{I^2}R + {Q_{\rm{C}}} + 0.5IT\left( {{\alpha _{\rm{H}}} - {\alpha _{\rm{C}}}} \right)}}{{{\alpha _{\rm{C}}}I + K}}, } $ | (2) |
| $ U = IR + \alpha \Delta T. $ | (3) |
其中
| $ \begin{array}{l} \;\;\;R = \rho l/A,\\ \;\;\;K = \kappa A/l,\\ \tau = \frac{{{\alpha _{\rm{H}}} - {\alpha _{\rm{C}}}}}{{{T_{\rm{H}}} - {T_{\rm{C}}}}}T, \end{array} $ |
式中:ρ为电阻率, κ为导热率, QC为制冷量, A为电偶臂横截面积, l为电偶臂长度.
对于式(2)中的T, 由于温度沿电偶臂是变化的, 且温度分布在电流不是太大时可视为线性分布, 因此, 令式(2)中的T为
| $ T = {T_{\rm{M}}} = \frac{{{T_{\rm{H}}} + {T_{\rm{C}}}}}{2}. $ |
由于材料参数是随温度变化的, 因此下面采用文献[6]中两种方法选取的材料参数来表征电偶臂材料性能.
1.2 TEC性能计算方法1用电偶臂两端的平均温度所对应的材料参数来表征材料的性能:
| $ \begin{array}{*{20}{l}} {{\alpha _{{\rm{M}}1}} = \alpha \left( {{T_{\rm{M}}}} \right), }\\ {{\rho _{{\rm{M}}1}} = \rho \left( {{T_{\rm{M}}}} \right), }\\ {{\kappa _{{\rm{M}}1}} = \kappa \left( {{T_{\rm{M}}}} \right).} \end{array} $ |
则电偶臂的电阻和热导为
| $ \begin{array}{*{20}{l}} {{R_{{\rm{M}}1}} = \frac{{{\rho _{{\rm{M}}1}}l}}{A}, }\\ {{K_{{\rm{M}}1}} = \frac{{{\kappa _{{\rm{M}}1}}A}}{l}.} \end{array} $ |
式(1)可写为
| $ \begin{array}{*{20}{c}} {{Q_{\rm{C}}} = {\alpha _{\rm{C}}}I{T_{\rm{C}}} - \frac{1}{2}{I^2}\frac{{{\rho _{{\rm{M}}1}}l}}{A} - \frac{{{\kappa _{{\rm{M}}1}}A}}{l}\left( {{T_{\rm{H}}} - {T_{\rm{C}}}} \right)}\\ { - \frac{1}{2}{T_{\rm{M}}}I\left( {{\alpha _{\rm{H}}} - {\alpha _{\rm{C}}}} \right).} \end{array} $ | (4) |
相应的制冷温度和电压分别为
| $ {T_{\rm{C}}} = \frac{{{K_{{\rm{M1}}}}{T_{\rm{H}}} + 0.5{I^2}{R_{{\rm{M1}}}} + 0.5{T_{\rm{M}}}I\left( {{\alpha _{\rm{H}}} - {\alpha _{\rm{C}}}} \right) + {Q_{\rm{C}}}}}{{{\alpha _{\rm{C}}}I + {K_{{\rm{M1}}}}}}, $ | (5) |
| $ U = I{R_{{\rm{M}}1}} + {\alpha _{{\rm{M}}1}}\left( {{T_{\rm{H}}} - {T_{\rm{C}}}} \right). $ | (6) |
采用电偶臂两端温度所对应材料参数的平均值来表征材料的性能:
| $ \begin{array}{*{20}{l}} {{\alpha _{{\rm{M}}2}} = \frac{{\alpha \left( {{T_{\rm{H}}}} \right) + \alpha \left( {{T_{\rm{C}}}} \right)}}{2}, }\\ \begin{array}{l} {\rho _{{\rm{M}}2}} = \frac{{\rho \left( {{T_{\rm{H}}}} \right) + \rho \left( {{T_{\rm{C}}}} \right)}}{2}, \\ {\kappa _{{\rm{M}}2}} = \frac{{\kappa \left( {{T_{\rm{H}}}} \right) + \kappa \left( {{T_{\rm{C}}}} \right)}}{2}. \end{array} \end{array} $ |
则电偶臂电阻和热导为
| $ \begin{array}{*{20}{l}} {{R_{{\rm{M}}2}} = \frac{{{\rho _{{\rm{M}}2}}l}}{A}, }\\ {{K_{{\rm{M}}2}} = \frac{{{\kappa _{{\rm{M}}2}}A}}{l}.} \end{array} $ |
电偶臂的制冷量为
| $ \begin{array}{*{20}{c}} {{Q_{\rm{C}}} = {\alpha _{\rm{C}}}I{T_{\rm{C}}} - \frac{1}{2}{I^2}\frac{{{\rho _{{\rm{M}}2}}l}}{A} - \frac{{{\kappa _{{\rm{M}}2}}A}}{l}\left( {{T_{\rm{H}}} - {T_{\rm{C}}}} \right)}\\ { - \frac{1}{2}{T_{\rm{M}}}I\left( {{\alpha _{\rm{H}}} - {\alpha _{\rm{C}}}} \right).} \end{array} $ | (7) |
相应的制冷温度和电压为
| $ {T_{\rm{C}}} = \frac{{{K_{{\rm{M2}}}}{T_{\rm{H}}} + 0.5{I^2}{R_{{\rm{M2}}}} + 0.5{T_{\rm{M}}}I\left( {{\alpha _{\rm{H}}} - {\alpha _{\rm{C}}}} \right) + {Q_{\rm{C}}}}}{{{\alpha _{\rm{C}}}I + {K_{{\rm{M}}2}}}}, $ | (8) |
| $ U = I{R_{{\rm{M}}2}} + {\alpha _{{\rm{M}}2}}\left( {{T_{\rm{H}}} - {T_{\rm{C}}}} \right). $ | (9) |
上述制冷温度式(5)、(8)两边同时含有TC, 给TC赋初始值, 通过迭代即可计算出收敛后的TC值, 然后即可通过式(6)、(9)计算电压.
2 热电材料参数的提取方法在TEC工作时, 式(4)、(7)中, TH和TC可直接测量, QC和I是施加的载荷, 因此, 其中的未知量就是随温度变化的材料参数.
目前, TEC常用的热电材料通常是性能最好的碲化铋合金, 其材料参数是随温度变化的, 且其性能随着温度的降低而变差, 这3个参数近似为温度的二次多项式的关系[23]:
| $ \begin{array}{l} \alpha = {a_0} + {a_1}T + {a_2}{T^2}, \\ \rho = {b_0} + {b_1}T + {b_2}{T^2}, \\ \mathit{\kappa } = {c_0} + {c_1}T + {c_2}{T^2}. \end{array} $ | (10) |
因此, 在对TEC不同工作状况进行测量后, 利用式(4)和(7), 分别可获得一个未知量为式(10)中九个系数的方程组.
由于各个厂家在材料中掺杂的成分和比例不同, 所以其材料参数也会有所差别.图 2是3组不同的热电材料参数随温度的变化关系[23-25], 其中, Melcor和Namic曲线分别为这两家公司热电材料所对应的参数, Handbook曲线为文献[23]中测得的参数.表 1为式(10)中的系数.
| 表 1 材料参数的系数 Tab. 1 Coefficients of material parameters |
由于表 1中的系数难以直观反映材料参数数值及确定上下限和约束条件, 同时, 由于TEC制冷时一般工作在室温至零下几十度(>-100℃), 为使从一级TEC提取的参数不至于在较低温度时表征的材料性能与实际相差过大, 可将式(10)改写为由三点确定的拉格朗日差值的形式, 以便于对这三点进行约束和设定上下限, 从而降低提取参数所表征材料性能的误差, 改写后形式如下:
| $ \begin{array}{l} \alpha = \left[ {{\alpha _{200}}(T - 250)(T - 300) + {\alpha _{300}}(T - 250)(T - } \right.\\ \;\;\;\;\;\;\left. {200) - 2{\alpha _{250}}(T - 200)(T - 300)} \right]/5\;000\\ \rho = \left[ {{\rho _{200}}(T - 250)(T - 300) + {\rho _{300}}(T - 250)(T - } \right.\\ \;\;\;\;\;\;\left. {200) - 2{\rho _{250}}(T - 200)(T - 300)} \right]/5\;000\\ \kappa = \left[ {{\kappa _{200}}(T - 250)(T - 300) + {\kappa _{300}}(T - 250)(T - } \right.\\ \left. {\;\;\;\;\;\;200) - 2{\kappa _{250}}(T - 200)(T - 300)} \right]/5\;000. \end{array} $ | (11) |
式中:α、ρ、κ的下标200、250、300为温度/K.制冷量式(4)和(7)中的变量即为200 K、250 K、300 K时的α、ρ、κ.
根据图 2, α、ρ、κ满足以下约束:
| $ \begin{array}{*{20}{l}} {{\alpha _{200}} < {\alpha _{250}} < {\alpha _{300}}, }\\ {{\rho _{200}} < {\rho _{250}} < {\rho _{300}}, }\\ {{\kappa _{200}} > {\kappa _{250}} > {\kappa _{300}}.} \end{array} $ | (12) |
其上下限可设为
| $ \begin{array}{l} \;\;\;\;\;\;lb = \left[ {1.4{{\rm{e}}^{ - 4}};1.7{{\rm{e}}^{ - 4}};1.8{{\rm{e}}^{ - 4}};5.0{{\rm{e}}^{ - 6}};5.0{{\rm{e}}^{ - 6}}} \right.;\\ \left. {7.0{{\rm{e}}^{ - 6}};1.8;1.5;1.4} \right]\\ \;\;\;\;\;\;ub = \left[ {1.9{{\rm{e}}^{ - 4}};2.1{{\rm{e}}^{ - 4}};2.3{{\rm{e}}^{ - 4}};8.0{{\rm{e}}^{ - 6}};1.0{{\rm{e}}^{ - 5}}} \right.;\\ \left. {1.2{{\rm{e}}^{ - 5}};2.5;2.1;1.8} \right], \end{array} $ | (13) |
此时, QC即可写为如下函数形式:
| $ \begin{array}{l} \;\;\;\;\;\;\;{Q_{\rm{C}}} = f\left( {I, {T_{\rm{C}}}, {T_{\rm{H}}}, {\alpha _{200}}, {\alpha _{250}}, {\alpha _{300}}, {\rho _{200}}, {\rho _{250}}, {\rho _{300}}} \right., \\ \left. {{\kappa _{200}}, {\kappa _{250}}, {\kappa _{300}}} \right). \end{array} $ | (14) |
通过实验, 可获得不同制冷量(QC1, QC2…QCn)时TEC在不同电流(I1, I2…Im)下的制冷温度, 这样就可获得一个由m*n个方程构成的方程组.本文对一级TEC在QC为0 W, 8 W, 13 W时, 对I从1 A到5 A每隔0.5 A进行测量, 共获得3*9个方程, 对由这27个方程构成的超定方程组在约束式(12)及上下限式(13)下, 利用最小二乘法进行求解, 即可获得200 K、250 K、300 K时的α、ρ、κ, 从而获得热电材料参数随温度的变化关系.
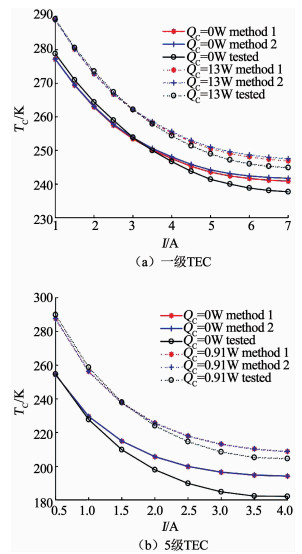
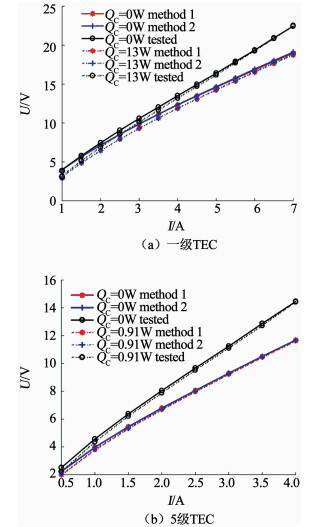
3 实验验证 3.1 计算方法准确度的验证由于电偶臂在电流不是太大时其沿长度的温度分布可视为线性变化, 而在电流过大(尤其是大于最大电流Imax)时, 电偶臂中间温度将显著高于两端的平均温度, 因此方法1和方法2在电流不是太大时所计算的材料参数有效性要比较好.采用两种方法对一级和5级TEC制冷温度和电压的计算结果与真空环境中的测试结果分别见图 3和图 4.
|
图 3 方法1和方法2计算的制冷温度与实验结果的对比 Fig. 3 Cooling temperature calculated by method 1 and method 2 compared with tested values |
|
图 4 方法1和方法2计算的电压与实验结果的对比 Fig. 4 Voltage calculated by method 1 and method 2 compared with tested values |
如图 3所示, 两种方法所计算的制冷温度非常接近, 都要高于实验值, 且当电流较大时, 冷热端温差也较大.由于材料参数是温度的二次多项式, 因此, 在较大温差下, 两种方法所采用的参数所表征的材料性能离真实性能差别也就越大.根据图 3, 整个制冷温度区间, 两种方法所表征的材料综合性能要低于材料实际性能.因此, 对于前面参数提取方法中所得到的方程组, 当各个参数采用实验中TEC的实测数值时, 所提取的材料参数所表征的材料综合性能要比材料实际性能更优, 因此, 利用所提取的材料参数计算另一款TEC性能时, 计算的制冷温度也要更低, 即更接近实测值.
对于电压, 无论一级还是5级TEC, 其计算结果都比实验值要低, 在电流分别为7 A和4 A时, 有最大相对误差, 分别为16.22%和19.27%.这主要有以下原因:一是电压公式中材料参数取值存在误差, 二是由于接触电阻大小难以确定, 因此计算电压时未考虑接触电阻的存在, 以上两点使得电压的计算值要小于实测值.
3.2 提取的参数有效性的验证为验证所提取的材料参数的有效性, 也就是所提取的材料参数能否有效计算其它相同热电材料TEC的性能, 下面用提取的材料参数对相同材料的一款5级TEC的性能进行计算, 计算的制冷温度和电压以及相应实验结果见图 5.对于此款5级TEC, 为保证较高的制冷系数, 其制冷量一般不会超过1 W.制冷量为0 W、0.45 W、0.91 W, I=4 A时, 厂家性能曲线给出的空气中制冷温度分别约为173.0 K、182.0 K、192.0 K;误差分别为9.1 K、11.0 K、12.5 K, 而实际测量中, 空气中的制冷温度要比真空中高10.0 K左右, 此时, 厂家提供的性能曲线误差将高达20.0 K.而在0~4 A电流区间, 方法1和方法2的最大误差分别为4.0 K、1.6 K、4.9 K和3.2 K、2.4 K、6.1 K.由此可见, 两种方法所提取的材料参数在计算另一款相同材料TEC的制冷温度时误差明显小于厂家性能曲线, 都有着较高的准确度.而对于电压, 由于计算模型的不准确性, 根据图 5(b), 两种方法电压计算值均有较大误差.
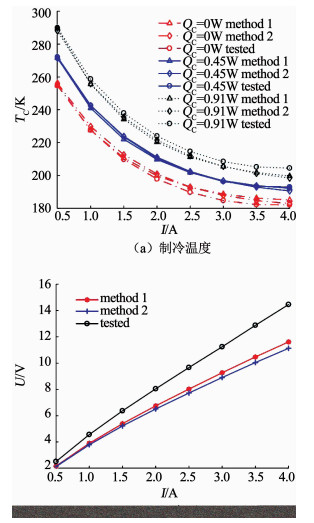
|
图 5 5级TEC制冷温度和电压计算值与实测值的对比 Fig. 5 Cooling temperature and voltage of five-stage TEC calculated by method 1 and method 2 compared with tested values |
为获得一级TEC电压计算中的电阻误差, 利用提取的材料参数对一级TEC的电压进行了再计算, 图 6(a)为QC=0 W时, 再计算电压与实测值的对比.由图 6(a)可知, 两种方法的再计算电压几乎重合, 与图 4(a)中计算结果非常接近.由于再计算电压的误差与电流并非线性相关, 而不同的电流又对应不同的制冷温度, 根据图 6(b), 电阻的误差与两端平均温度近似为线性关系.为此, 用随平均温度线性变化的电阻对式(6)和式(9)计算的电压进行修正, 即可得式(15)和式(16), 利用式(15)和式(16)建立两组方程, 即可提取出一级TEC计算中电阻误差随温度的变化关系.
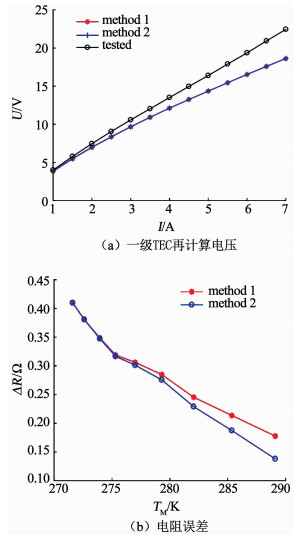
|
图 6 一级TEC再计算的电压和电阻误差 Fig. 6 Recalculated voltage and electric resistance of one-stage TEC |
| $ {U = I{R_{{\rm{M1}}}} + {\alpha _{{\rm{M1}}}}\left( {{T_{\rm{H}}} - {T_{\rm{C}}}} \right) + {R_{11}}{T_{{\rm{M1}}}} + {R_{10}}, } $ | (15) |
| $ {U = I{R_{{\rm{M}}2}} + {\alpha _{{\rm{M}}2}}\left( {{T_{\rm{H}}} - {T_{\rm{C}}}} \right) + {R_{21}}{T_{{\rm{M}}2}} + {R_{20}}.} $ | (16) |
利用提取出的电阻误差对5级TEC计算电压进行修正后的结果与实验值对比如图 7所示.修正后的电压误差有着较大程度的改善, 在TEC适宜工作电流区间内, 方法1的计算误差 < 4.80%, 方法2的计算误差 < 7.00%.
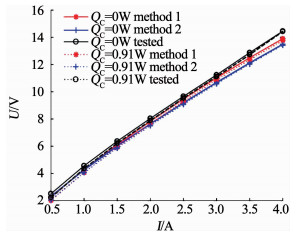
|
图 7 修正后的电压与实测值对比 Fig. 7 Comparison of the modified voltage and tested values |
表 2为本文方法与其他几种5级TEC性能计算结果的误差对比.其中, 制冷温度误差为QC=0 W、0.53 W、0.91 W时的最大误差.本文方法制冷温度和电压的误差约为极值法[13]的1/5~1/2, 与有限元法利用参数实测值计算的误差近似, 比有限元法利用参数提取值计算的结果误差略大[22], 但尚在可接受的范围, 且本文方法有计算简单、计算量小的优势.而厂家在2017年公布的制冷温度(空气中)要比实测值(空气中)低25 K以上, 2019年更新的参数虽然准确度有所提高, 但误差仍达23 K以上, 电压的最大误差均可达10%以上, 由此可见,对TEC性能的预评估对TEC的选型是非常有必要的.
| 表 2 几种TEC计算结果准确度对比 Tab. 2 Accuracy of TEC performance calculated by several methods |
由此可见, 利用本文方法从一级TEC提取的材料参数在计算另一款5级TEC性能时, 无论制冷温度还是电压, 都有较高的准确度.在无法获取材料参数实测值情况下, 可对一款一级TEC进行实验测试(通常厂家提供的一级TEC是最便宜、型号最多的), 通过本文方法提取出TEC的材料参数, 然后用于其他相同材料TEC的性能评估或结构优化, 从而选择出更合适的TEC.
4 结论1) 通过对一级和5级TEC制冷温度的测量, 说明TEC的实测制冷温度通常难以达到厂家标称值, 且误差随级数的增加而增大, 这在TEC选型时应尤为注意.
2) 利用两种计算方法所提取的材料参数可有效的表征热电材料的性能, 在用于计算其它相同材料TEC性能时有较高的准确度.
3) TEC电压计算中, 接触电阻的存在是不容忽视的, 接触电阻与温度相关, 在考虑该电阻后可明显改善计算电压的准确度.
| [1] |
MIYAGUCHI K, SUZUKI H, DEZAKI J, et al. CCD developed for scientific application by Hamamatsu[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 1999, 436(1): 24. DOI:10.1016/s0168-9002(99)00595-1 |
| [2] |
CHENG Y H, SHIH C. Maximizing the cooling capacity and COP of two-stage thermoelectric coolers through genetic algorithm[J]. Applied Thermal Engineering, 2006, 26: 937. DOI:10.1016/j.applthermaleng.2005.09.016 |
| [3] |
JEONG E S. A new approach to optimize thermoelectric cooling modules[J]. Cryogenics, 2014, 59: 38. DOI:10.1016/j.cryogenics.2013.12.003 |
| [4] |
WANG Xiaodong, WANG Qiuhong, XU Jinling. Performance analysis of two-stage TECs (thermoelectric coolers) using a three-dimensional heat-electricity coupled model[J]. Energy, 2014, 65: 419. DOI:10.1016/j.energy.2013.10.047 |
| [5] |
李玉东.半导体多级制冷性能组合优化设计[D].上海: 同济大学, 2007 LI Yudong. Combined optimal design on performance of milti-stage semiconductor cooling[D]. Shanghai: Tongji University, 2007 http://cdmd.cnki.com.cn/article/cdmd-10247-2008019318.htm |
| [6] |
何凯. EMCCD相机致冷技术研究[D].北京: 中国科学院大学, 2015 HE Kai. Research on cooling technique for EMCCD camera[D]. Beijing: University of Chinese Academy of Sciences, 2015 http://cdmd.cnki.com.cn/Article/CDMD-80151-1015951650.htm |
| [7] |
Riffat S B, Ma X, Wilson R. Performance simulation and experimental testing of a novel thermoelectric heat pump system[J]. Applied Thermal Engineering, 2006, 26(5-6): 494. DOI:10.1016/j.applthermaleng.2005.07.016 |
| [8] |
LUO Zhaoxia. A simple method to estimate the physical characteristics of a thermoelectric cooler from vendor datasheets[J]. Electronics Cooling, 2008, 14: 22. |
| [9] |
Focklai Tan, FOK S C. Methodology on sizing and selecting thermoelectric cooler from different TECmanufacturers in cooling system design[J]. Energy Convers Manage, 2008, 49: 1715. DOI:10.1016/j.enconman.2007.11.001 |
| [10] |
ZHANG Hengyun. A general approach in evaluating and optimizing thermoelectric coolers[J]. International Journal of Refrigeration, 2010, 33(6): 1187. DOI:10.1016/j.ijrefrig.2010.04.007 |
| [11] |
LINEYKIN S, BEN-YAAKOV S. Modeling and analysis of thermoelectric modules[J]. IEEE Transactions on Industrial Applications, 2007, 43(2): 505. DOI:10.1109/TIA.2006.889813 |
| [12] |
CHEN Min, SNYDER G J. Analytical and numerical parameter extraction for compact modeling of thermoelectric coolers[J]. International Journal of Heat and Mass Transfer, 2013, 60: 689. DOI:10.1016/j.ijheatmasstransfer.2013.01.020 |
| [13] |
LEE H S, ATTAR A M, WEERA S L. Performance prediction of commercial thermoelectric cooler modules using the effective material properties[J]. Journal of Electronic Materials, 2015, 44(6): 2157. DOI:10.1007/s11664-015-3723-7 |
| [14] |
PALACIOS R, ARENAS A, Pecharromn R R, et al. Analytical procedure to obtain internal parameters from performance curves of commercial thermoelectric modules[J]. Applied Thermal Engineering, 2009, 29(17): 3501. DOI:10.1016/j.applthermaleng.2009.06.003 |
| [15] |
DZIURDZIA P, BRATEK P, BRZOZOWSKI I, et al. Extraction of temperature dependent parameters for an electrothermal model of thermoelectric energy harvester[C]//Mixed Design of Integrated Circuits & Systems, Mixdes-international Conference. IEEE, 2016. DOI: 10.1109/MIXDES.2016.7529769
|
| [16] |
HUANG B, CHIN C, DUANG C L. A design method of thermoelectric cooler[J]. International Journal of Refrigeration, 2000, 23(3): 208. DOI:10.1016/s0140-7007(99)00046-8 |
| [17] |
ANATYCHUK LI, HAVRYLYUK MV. Procedure and equipment for measuring parameters of thermoelectric generator modules[J]. Journal of Electronic Materials, 2011, 40(5): 1292. DOI:10.1007/s11664-011-1619-8 |
| [18] |
戴维涵, 代彦军, 张鹏, 等. 半导体制冷元件特性参数测量及选用[J]. 上海交通大学学报, 2004, 38(10): 1669. DAI Weihan, DAI Yanjun, ZHANG Peng, et al. Measurment for the characteristic parameters and selection of thermoelectric modules[J]. Journal of Shanghai Jiao Tong University, 2004, 38(10): 1669. DOI:10.3321/j.issn:1006-2467.2004.10.016 |
| [19] |
MITRANI D, TOME J A, SALAZAR J, et al. Methodology for extracting thermoelectric module parameters[J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(4): 1548. DOI:10.1109/tim.2005.851473 |
| [20] |
AHISKA R, Dişlitaş S. Computer controlled test system for measuring the parameters of the real thermoelectric[J]. Energy Conversion Management, 2011, 52(1): 27. DOI:10.1016/j.enconman.2010.06.023 |
| [21] |
Chu E T, Chien H C, Hsieh H L, et al. A novel method to rapidly determine the key properties of thermoelectric devices[C]//2012 13th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm). IEEE, 2012. DOI: 10.1109/ITHERM.2012.6231418
|
| [22] |
NIE S J, WANG M F, GAO X D, et al. Extraction of temperature-dependent thermoelectric material parameters of a thermoelectric cooler by the non-linear least squares method[J]. Energies, 2019, 12(1): online. DOI:10.3390/en12010169 |
| [23] |
ROWE D M. CRC handbook of thermoelectrics[M]. 4th ed. Boca Raton, Florida: CRC Press, 1995, Chapter 14.3
|
| [24] |
XUAN X C, NG K C, YAP C, et al. The maximum temperature difference and polar characteristic of two-stage thermoelectric coolers[J]. Cryogenics, 2002, 42(5): 273. DOI:10.1016/s0011-2275(02)00035-8 |
| [25] |
namic官网.[OL].[accessed 15 January 2018]. http://www.thermonamic.com/
|
 2019, Vol. 51
2019, Vol. 51


