随着城市经济的快速增长和城市机动车保有量不断增多，城市道路日益突显，为此寻求合理的措施缓解城市交通问题迫在眉睫.交叉口作为城市道路网络最为直接的瓶颈点，聚焦交叉口的运行状况，优化信号交叉口控制方案是改善城市道路交通网络的重要方式之一^[1-2].交叉口信号控制方案包含两要素：可行相位组合(相位流线组合、相序)和相位配时，最优的控制方案必须同时确保相位组合和相位配时均与交叉口车辆特性相协调，仅通过优化相位配时而不考虑相位组合的合理性，并不能真正意义上提升交叉口控制效率.

城市交叉口控制优化是一个传统而又不断发展的课题，近年来，交叉口信号优化控制研究众多.对于固定信号控制方式，信号交叉口的研究主要集中于如何优化信号相位配时，通过选取不同指标建立相应的目标模型进行优化研究，如延误最小^[3-4]，通行能力最大^[5-6]，停车次数最少^[7]，排队长度最短^[8-9]以及延误、通行能力、停车次数等多个指标综合最优^[10-11]，然后对模型进行求解从而得到最优的相位配时.随着感应信号控制和自适应信号控制的提出，研究者以固定相位组合为前提，从相位时长的角度研究最佳的最大最小绿灯时间和单位延长时间以进一步改善交叉口车流通行状态^[12-13].虽然研究者主要集中关注于如何优化交叉口相位配时，但也有少部分学者分析研究相位组合，以改善信号控制方案，如文献[14]认为相位相序安排不适应造成的交叉口时空资源损失和事故隐患越来越多; 再有根据交叉路口各方向的交通量在不同时刻是不同，提出交叉口相序优化^[15]以及单交通路口变相位变周期信号控制^[16]，这些研究均表明信号相位组合会影响信号控制效果，由此有必要对交叉口信号控制方案的相位组合展开研究.

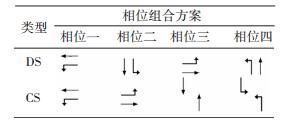
现有的十字交叉口信号控制研究中，控制相位采用的基本都是传统的相位组合方案，具体为对向式(OS)和分流式(DS)，或两者组合式(CS)的相位组合方案，这些相位组合方案中，当出现相位两组合流线排队长度并不相近时，即该相位绿灯放行一段时间后将会出现排队长的流线车辆以饱和流率通行，而另一流线车辆以到达率通行(非饱和情况下，流线车辆到达率小于饱和流率)，由此造成相位绿灯时间损失.

随着研究的深入与改进，为避免相位绿灯损失，学者提出了相位流线搭接，即交叉口信号相位由传统的两流线组合但相位之间不存在相同流线的组合方式，转变成为相位流线搭接(即同一流线跨越多个相位)方式.相位流线搭接方式相比传统控制方式是控制方式的改进，主要在于采用相位流线搭接方式能够减少相位绿灯损失.因此，在相位流线搭接能够进一步优化信号控制的基础上，有学者综合流线对向相容和分流相容关系，提出了相位流线组合环栅结构(RBS)^[17].

目前，环栅结构是采用最为广泛的信号相位流线组合方法，其优点在于完美结合了流线的对向相容关系和分流相容关系，并灵活的实现流线搭接，保证相位绿灯时间得到充分利用，为信号控制相位组合方案的生成提供了很大便利.但其局限在于未考虑流线合流相容关系(具体合流相容描述见1.1节)，致使相位流线组合不全面，进而控制相位组合方案不全面，因此不能确保选取的控制方案为最优相位控制方案.基于此，有必要寻求一种全面的最优信号控制方案的确定算法，综合考虑流线搭接，实现信号控制方案与流线流量到达进一步匹配.

1 交叉口相位流线组合 1.1 流线相容关系

在不考虑设置许可相位的前提下，交叉口信号控制是通过设置相位使交叉口内冲突流线进行时间分离，以保障交通安全.而交叉口信号相位由不同流线组合而成，为了保证各冲突流线车辆在不同的时间系列获得交叉口通行路权，单个相位内流线的关系则必须为非冲突关系，即相容关系.按照右行规则，且常规左转流向车道位于直行流向车道左侧的原则布置前提下，交叉口流线的关系有分流关系、对向关系和合流关系，所有流线的分流关系均为相容关系，但并不是所有的对向关系和合流关系均为相容关系.因此，需对流线的相容关系进行细化，确定好流线相容关系，流线的相容组合即可作为相位流线组合.

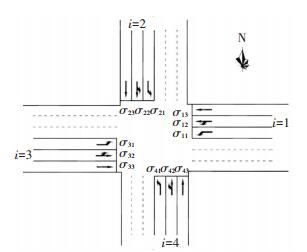
本文以十字交叉口为研究对象，将十字交叉口各进口用i表示，i=1、2、3、4分别代表东、北、西、南进口; 各股流线采用σ_ij(i=1、2、3、4，j=1、2、3)表示，将十字交叉口可能出现的所有流线用对应符号表示，并列于图 1.从图 1中可以看出j=2时，即σ_i2为流向共用车道所产生流线，其他符号代表单一流向的流线.根据右行规则本文暂不考虑右转流线.

对于常规的十字交叉口而言，交叉口并不一定存在图 1中的所有流线，故引入交叉口流线集合M，并对交叉口流线采用图 1对应符号表示，定义流线存在符号e_ij为

$ {e_{ij}} = \left\{ \begin{array}{l} 0,{\sigma _{ij}} \notin \mathit{\boldsymbol{M}};\\ 1,{\sigma _{ij}} \in \mathit{\boldsymbol{M}}. \end{array} \right. $

(1)

流线分流关系是交叉口同一进口内流线之间的相互关系; 定义流线分流关系组集合为A，有

$ \mathit{\boldsymbol{A}} = \left\{ {{\mathit{\boldsymbol{A}}_\alpha },\alpha \in {N^ * }} \right\}. $

(2)

对于十字交叉口有 α = 1、2、3、4,A_α 为交叉口某一进口的流线集合，有

$ {\mathit{\boldsymbol{A}}_\alpha } = \left( {{\sigma _{\alpha j}}\left| {{\sigma _{\alpha j}} \in } \right.} \right.\left. M \right\}. $

(3)

为了更好地描述集合A_α内流线的相容关系，对应引入参数a_α，有

$ {a_\alpha } = \left\{ \begin{array}{l} 1,相容;\\ 0,不相容. \end{array} \right. $

(4)

式中：a_α=1代表其对应的流线分流关系组A_α内的流线相容，a_α=0代表其对应的流线分流关系组A_α内的流线不相容.一般情况下，在左转流向车道设置于直行流向车道左侧前提下可知集合A_α内的流线均相容，故有$ {{a}_{\alpha }}\equiv 1, \forall \alpha $.

此外，流线对向关系指的是分别位于对立两进口且流线对应的流向为相反方向的流线间相互关系; 由此定义流线对向关系组集合为

$ \mathit{\boldsymbol{B}} = \left\{ {{\mathit{\boldsymbol{B}}_\beta },\beta \in {N^ * }} \right\}. $

(5)

一般情况下，这些对向关系组内的流线被作为相容关系考虑，但是当B_β中存在流线对应的流向与交叉口另一流向车道共用时，则该流线对向关系组两流线不相容，引入参数b_β，有

$ {b_\beta } = \left\{ \begin{array}{l} 1,{\sigma _{ij\left| {{e_{i2}} = 1} \right.}} \notin {\mathit{\boldsymbol{B}}_\beta };\\ 0,{\sigma _{ij\left| {{e_{i2}} = 1} \right.}} \in {\mathit{\boldsymbol{B}}_\beta }. \end{array} \right. $

(6)

式中：b_β=1代表其对应的流线对向关系组B_β内的流线相容，b_β=0代表其不相容，$ {{\sigma }_{ij|{{e}_{i2}}=1}}$代表存在流线车道共用的进口i内流线.

最后，流线之间还存在合流关系，对于流线合流关系指的是相邻两进口的流线汇入至同一交叉口出口的两流线关系，由此定义流线合流关系组集合为

$ \mathit{\boldsymbol{C = }}\left\{ {{\mathit{\boldsymbol{C}}_\gamma },\gamma \in {N^ * }} \right\}. $

(7)

式中：C_γ为两合流关系流线的集合，γ为C_γ内两合流关系流线共同汇入的交叉口出口编号，引入参数c_γ，定义

$ {c_\gamma } = \left\{ \begin{array}{l} 1,相容;\\ 0,不相容. \end{array} \right. $

(8)

现阶段流线的合流关系被视为冲突关系，即意味着c_γ≡0.但本文将流线的合流关系细化，当C_γ中存在流线对应的流向与交叉口另一流向车道共用时，则该合流关系组中两流线不相容，即如果${\sigma _{ij|{e_{i2}} = 1}} \in {\mathit{\boldsymbol{C}}_\gamma } $，则对$\forall \gamma $有c_γ=0;但当流线合流关系组C_γ中不包含流线$ {\sigma _{ij|{e_{i2}} = 1}}$时，也不一定意味着C_γ中的两流线相容，需进一步细化.

如果C_γ中两流线相容，须同时满足两个条件：1)两流线所对应的流向与其他流向均不存在车道共用，即${\sigma _{ij|{e_{i2}} = 1}} \notin {\mathit{\boldsymbol{C}}_\gamma } $; 2)互为合流关系的两流线所占交叉口进口车道数与对应出口车道数相匹配，即${N_C}_{_\gamma }\left( 1 \right) + {N_C}_{_\gamma }\left( 2 \right) \le {N_\gamma }, {N_C}_{_\gamma }\left( 1 \right)、{N_{\mathit{\boldsymbol{C}}}}_{_\gamma }\left( 2 \right) $分别代表集合C_γ中两元素(流线)所对应的车道数; N_γ为集合C_γ中两元素(流线)所对应交叉口出口γ的总车道数.

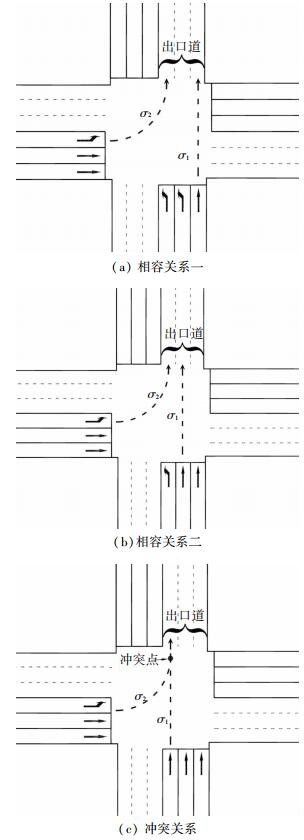
对于条件2的解释如图 2所示.假设任意互为合流关系的两条流线σ₁和σ₂, 对应的车道数分别为N_σ1和N_σ2，其所对应的出口车道数为N_γ.则图 2(a)中有N_σ1=1, N_σ2=1, N_γ=3，故N_σ1+N_σ2 < N_γ，满足条件2，流线σ₁和σ₂相容; 同样图 2(b)中$ {N_{{\sigma _1}}} = 2, {N_{{\sigma _2}}} = 1, {N_\gamma } = 3$, 故${N_{{\sigma _1}}} + {N_{{\sigma _2}}} = {N_\gamma } $，满足条件2，流线σ₁和σ₂相容; 图 2(c)中${N_{{\sigma _1}}} = 3, {N_{{\sigma _2}}} = 1, {N_\gamma } = 3 $, 显然$ {N_{{\sigma _1}}} + {N_{{\sigma _2}}} > {N_\gamma }$，不满足条件2，即流线σ₁和σ₂所占进口车道数与交叉口出口γ的总车道数不相匹配，合流关系流线σ₁和σ₂存在冲突点，故流线σ₁和σ₂不相容.

由此，集合C_γ中两合流关系流线相容，需满足

$ \left\{ \begin{array}{l} {\sigma _{ij\left| {{e_{i2}} = 1} \right.}} \notin {\mathit{\boldsymbol{C}}_\gamma };\\ {N_{{\mathit{\boldsymbol{C}}_\gamma }\left( 1 \right)}} + {N_{{\mathit{\boldsymbol{C}}_\gamma }\left( 2 \right)}} \le {N_\gamma }. \end{array} \right. $

(9)

满足式(9)情况下，有流线合流关系组C_γ所对应的参数c_γ=1.

1.2 流线相容组集合

综上，确定交叉口所有流线间的分流关系、对向关系以及合流关系后，并对其进行相容性判断，从而得到交叉口所有流线相容组集合为

$ \mathit{\boldsymbol{H}} = \left\{ {{\mathit{\boldsymbol{A}}_{\alpha \left| {{a_\alpha } = 1} \right.}}} \right\} \cup \left\{ {{\mathit{\boldsymbol{B}}_{\beta \left| {{b_\beta } = 1} \right.}}} \right\} \cup \left\{ {{\mathit{\boldsymbol{C}}_{\gamma \left| {{c_\gamma } = 1} \right.}}} \right\}. $

(10)

式中$ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{}}_{\alpha |{a_\alpha } = 1}}$表示所有a_α=1所对应的组合，$\mathit{\boldsymbol{B}}{_{\beta |{b_\beta } = 1}} $与$\mathit{\boldsymbol{C}}{_{\gamma |{c_\gamma } = 1}} $同样.

根据流线相容关系，即为两流线之间不存在相互交叉点，也就是这两股交通流线对应的车流在交叉口区域可同时获得通行权，与信号相位流线组合的设置要求一致，故交叉口每一相容流线组合均可作为一个信号相位，即集合H的每一元素均可作为一个相位流线组合.

2 信号最优控制方案

交叉口信号最优控制方案包括可行相位组合和信号相位配时，确定可行相位组合方案之前必须先得到所有的相位组合，然后从中选取满足交叉口信号控制相位方案设置条件的相位组合方案作为可行相位组合方案.

2.1 信号相位组合

所谓的信号相位组合方案即是由某些个零散相位按照一定顺序排列组合而成.由于集合中的元素具有无序性的特性，而对于交叉口信号相位组合方案而言，信号控制相位组合方案的设置具有相序的要求，故本文引入数组来对交叉口信号控制相位组合方案进行描述，所谓数组，即是相同数据类型的元素按一定顺序排列的集合.

集合H中元素即代表了交叉口零散相位，对这些零散相位进行随机抽样排列可以得到一系列的相位组合方案，每一信号相位组合方案采用字符数组表示，即$\mathit{\boldsymbol{P}}{_\upsilon }\left[ {{m_\upsilon }} \right] $，则有

$ \mathit{\boldsymbol{P = }}\left\{ {{\mathit{\boldsymbol{P}}_\upsilon }\left[ {{m_\upsilon }} \right],\upsilon \in {N^ * }\;且\;{m_\upsilon } \in {N^ * }} \right\}. $

(11)

式中：P为所有的信号相位组合方案构成的集合; υ为相位组合方案编号，有$ {\rm{max}}~~\upsilon = \sum\limits_{w = 1}^{\left| H \right|} {} C_{|H|}^wA_w^w, w \in {N^*}{m_\upsilon }$为对应相位组合方案相位数，也即数组元素个数，有$ {\rm{max}}~~{m_\upsilon } = \left| {{\rm{ }}\mathit{\boldsymbol{H}}{\rm{ }}} \right|$.

所有的信号相位组合方案确定后，并不是每一个信号相位组合方案均能满足交叉口信号控制方案的设置要求，由此有必要从中获取满足交叉口信号控制设置要求的相位组合方案.

2.2 可行相位组合方案

信号相位组合方案要成为可行相位组合方案必须满足具体交叉口信号控制相位设置要求：1)为了保证周期内所有流线均获得通行权，相位组合方案必须包含交叉口所有流线，即$ \mathop \cup \limits_{\delta = 0}^{{m_\upsilon } - 1} {\rm{ }}\mathit{\boldsymbol{P}}{_\upsilon }\left[ \delta \right] = {\rm{ }}\mathit{\boldsymbol{M}}, \delta \in N$; 2)同一流线占用多个相位时，考虑流线搭接，保证流线放行连续性，这些相位必须为相邻相位.同时满足这两个条件的相位组合方案才能作为信号控制可行相位组合方案.

对于要求2，信号相位组合方案数组$ {P_\upsilon }[{m_\upsilon }]$存在两种情况均可视为满足要求2：

1) 除了相邻元素允许存在共同流线，其他元素间均不存共同流线，即对于$\forall \left| {\psi - \varphi } \right| \ge 2 $，有

$ {\mathit{\boldsymbol{P}}_\upsilon }\left[ \psi \right] \cap {\mathit{\boldsymbol{P}}_\upsilon }\left[ \varphi \right] = \emptyset . $

(12)

2) 除了相邻元素允许存在共同流线之外，若相隔1个元素间的两元素存在共同流线，即$\left| {\psi - \varphi } \right| = 2, P{_\upsilon }\left[ \psi \right] \cap {\rm{ }}P{_\upsilon }\left[ \varphi \right] \ne \emptyset $.则必须保证该两元素与其两中间元素三者之间存在同一流线，有

$ {\mathit{\boldsymbol{P}}_\upsilon }\left[ \psi \right] \cap {\mathit{\boldsymbol{P}}_\upsilon }\left[ {\frac{{\psi + \varphi }}{2}} \right] \cap {\mathit{\boldsymbol{P}}_\upsilon }\left[ \varphi \right] \ne \emptyset . $

(13)

此外其他元素间也均不存在共同流线.对于$ \forall \left| {\psi - \varphi } \right| \ge 3$，有

$ {\mathit{\boldsymbol{P}}_\upsilon }\left[ \psi \right] \cap {\mathit{\boldsymbol{P}}_\upsilon }\left[ \varphi \right] = \emptyset . $

(14)

式中$\psi \ne \varphi , \psi , \varphi $均为${\mathit{\boldsymbol{P}}_\upsilon }[{m_\upsilon }] $内元素编号，则$\psi \in N, \varphi \in N $，且$ \psi \in \left[ {0, {m_\upsilon } - 1} \right], \varphi \in [0, {m_\upsilon } - 1]$.

由此，相位组合方案数组$ {\mathit{\boldsymbol{P}}_\upsilon }[{m_\upsilon }]$要成为可行相位组合方案，在满足要求1的前提下，必须满足式(12)或者同时满足(13)、(14).

依次对相位组合方案数组$ {\mathit{\boldsymbol{P}}_\upsilon }[{m_\upsilon }]$进行条件判断，$\upsilon \in [0, \sum\limits_{w = 1}^{\left| H \right|} {} C_{|H|}^wA_w^w] $，即可得到可行相位组合方案.

通过此算法得到的相位组合方案数更为全面，不仅仅融合了环栅结构的所有优点，即包含了环栅结构所能得到的所有相位组合数和考虑了相位间流线搭接，同时进一步细化了交叉口流线间的相容关系.

本文对交叉口流线间的相容性进行细致讨论，得到了所有的流线相容组合情况，并根据交叉口信号相位方案的设置要求，确定了所有可行相位组合方案为

$ \mathit{\boldsymbol{F}} = \left\{ {{\mathit{\boldsymbol{F}}_w}\left[ {{m_w}} \right],w \in {N^ * }\;且\;{m_w} \in {N^ * }} \right\}. $

(15)

式中w为集合F内元素个数，每一元素即可视为一数组，记为${\mathit{\boldsymbol{F}}_w}[{m_w}] $，每一数组即代表一个可行相位组合方案，数组元素个数m_w即为对应第w个可行相位组合方案的相位数.

确定F后，一个完整的交叉口信号控制方案不仅仅只有相位组合方案，还有与之对应的信号配时方案.现阶段，在交叉口信号相位确定的前提下，信号优化配时方法众多，如Webster配时模型，HCM2010计算模型等.因此，本文借助运用较为广泛的HCM2010配时模型^[18]，对文中所提方法确定的相位组合方案进行配时，该模型对应的输入参数有相位流线组合方案，各流线流量到达，各流线饱和流率等，在这些参数确定的情况下，通过模型计算可得到对应流线的有效绿灯时间，再结合启动损失及黄灯时间，即可确定流线绿灯时长.篇幅原因，不详细列出具体的信号配时模型.

通过计算不同信号控制方案对应的车辆平均延误，对比车辆平均延误值，选取最小车辆平均延误所对应的信号控制方案作为交叉口最优控制方案，从而得到真正意义上的信号交叉口最优控制方案.

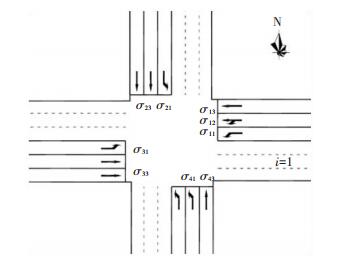
3 算例验证分析

为了验证本文所提方法的可行性，对一确定的交叉口进行验证分析.交叉口的流线车道布局及流线对应符号如图 3所示.

交叉口的流线集合$\mathit{\boldsymbol{M}}{\rm{ }} = \{ {\sigma _{11}}, {\sigma _{12}}, {\sigma _{13}}, {\sigma _{21}}, {\sigma _{23}}, {\sigma _{31}}, {\sigma _{33}}, {\sigma _{41}}, {\sigma _{43}}\} $，由此有${e_{11}} = {e_{12}} = {e_{13}} = {e_{21}} = {e_{23}} = {e_{31}} = {e_{33}} = {e_{41}} = {e_{43}} = 1, {e_{22}} = {e_{32}} = {e_{42}} = 0 $.

确定流线相容性的其他相关参数符号取值情况，具体取值：$\mathit{\boldsymbol{A}}{_1} = \left\{ {{\sigma _{11}}, {\sigma _{12}}, {\sigma _{13}}} \right\}, $ $ {\rm{ }}\mathit{\boldsymbol{A}}{_2} = \left\{ {{\sigma _{21}}, {\sigma _{23}}} \right\},$ $ \mathit{\boldsymbol{A}}{_3} = \left\{ {{\sigma _{31}}, {\sigma _{33}}} \right\}, $ $ \mathit{\boldsymbol{A}}{_4} = \left\{ {{\sigma _{41}}, {\sigma _{43}}} \right\}, $ $ {\rm{ }}\mathit{\boldsymbol{A}} = \left\{ {\left\{ {{\sigma _{11}}, {\sigma _{12}}, {\sigma _{13}}} \right\}{\rm{ }}\left\{ {{\sigma _{21}}, {\sigma _{23}}} \right\}, \left\{ {{\sigma _{31}}, {\sigma _{33}}} \right\}, \left\{ {{\sigma _{41}}, {\sigma _{43}}} \right\}} \right\}$ $,{a_1} = {a_2} = {a_3} = {a_4} = 1 $ ，则$\mathit{\boldsymbol{A}}_{\alpha |{a_\alpha }{\rm{ }} = 1} = \left\{ {\left\{ {{\sigma _{11}}, {\sigma _{12}}, {\sigma _{13}}} \right\},\left\{ {{\sigma _{21}}, {\sigma _{23}}} \right\},\left\{ {{\sigma _{31}}, {\sigma _{33}}} \right\}, \left\{ {{\sigma _{41}}, {\sigma _{43}}} \right\}} \right\}. $ $ {\rm{ }}\mathit{\boldsymbol{B}}{_1} = \left\{ {{\sigma _{11}}, {\sigma _{31}}} \right\},$ $\mathit{\boldsymbol{B}}{_2} = \left\{ {{\sigma _{13}}, {\sigma _{33}}} \right\} ,$ $ \mathit{\boldsymbol{B}}{_3} = \left\{ {{\sigma _{21}}, {\sigma _{41}}} \right\}, {\rm{ }}\mathit{\boldsymbol{B}}{_4} = \left\{ {{\sigma _{23}}, {\sigma _{43}}} \right\}$ $ \mathit{\boldsymbol{, B}} = \left\{ {\left\{ {{\sigma _{11}}, {\sigma _{31}}} \right\}, \left\{ {{\sigma _{13}}, {\sigma _{33}}} \right\}, \left\{ {{\sigma _{21}}, {\sigma _{41}}} \right\}, \left\{ {{\sigma _{23}}, {\sigma _{43}}} \right\}} \right\}, $ ${b_1} = 0, {b_2} = 0, {b_3} = 1, {b_4} = 1 $，则$ \mathit{\boldsymbol{B}}_{\beta {\rm{ }}|{b_\beta }{\rm{ }} = 1} = \left\{ {\left\{ {{\sigma _{21}}, {\sigma _{41}}} \right\}, \left\{ {{\sigma _{23}}, {\sigma _{43}}} \right\}} \right\},$ $ \mathit{\boldsymbol{C}}{_1} = \left\{ {{\sigma _{11}}, {\sigma _{23}}} \right\}, \mathit{\boldsymbol{C}}{_2} = \left\{ {{\sigma _{13}}, {\sigma _{41}}} \right\}, \mathit{\boldsymbol{C}}{_3} = \left\{ {{\sigma _{21}}, {\sigma _{33}}} \right\},$ $ \mathit{\boldsymbol{C}}{_4} = \left\{ {{\sigma _{31}}, {\sigma _{43}}} \right\}, \mathit{\boldsymbol{C}}{\rm{ }} = \left\{ {\left\{ {{\sigma _{11}}, {\sigma _{23}}} \right\}, \left\{ {{\sigma _{13}}, {\sigma _{41}}} \right\}, \left\{ {{\sigma _{21}}, {\sigma _{33}}} \right\}, \left\{ {{\sigma _{31}}, {\sigma _{43}}} \right\}} \right\} $.同样${c_1} = 0, {c_2} = 0, {c_3} = 1, {c_4} = 1, C_{\gamma |{c_\gamma }{\rm{ }} = 1} = \left\{ {\left\{ {{\sigma _{21}}, {\sigma _{33}}} \right\}, \left\{ {{\sigma _{31}}, {\sigma _{43}}} \right\}} \right\} $.由此可以确定交叉口所有流线相容组合H为$\{ \left\{ {{\sigma _{11}}, {\sigma _{12}}, {\sigma _{13}}} \right\}, \left\{ {{\sigma _{21}}, {\sigma _{23}}} \right\}, \left\{ {{\sigma _{31}}, {\sigma _{33}}} \right\}, \left\{ {{\sigma _{41}}, {\sigma _{43}}} \right\}, \left\{ {{\sigma _{21}}, {\sigma _{41}}} \right\}, \left\{ {{\sigma _{23}}, {\sigma _{43}}} \right\}, \left\{ {{\sigma _{21}}, {\sigma _{33}}} \right\},$$\{ {\sigma _{31}},{\sigma _{43}}\}\}$.

确定交叉口流线相容组合后，可以得到交叉口可行相位组合方案集合F，集合F内元素为一系列字符数组组成，记为$ {\mathit{\boldsymbol{F}}_w}[{m_w}]$，每一数组即代表一个可行的信号相位组合方案，通过编程计算本实例的可行信号相位组合方案总数为400个，其中四相位方案48个，五相位方案264个，六相位方案88个，部分可行相位组合方案见表 1.

确定交叉口可行相位组合方案集合后，结合流线流量分析交叉口最优信号控制方案.假定算例交叉口进口1~4的左转和直行交通流量依次为：375、375 pcu/h; 200、400 pcu/h; 250、700 pcu/h; 700、300 pcu/h.

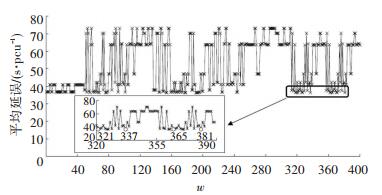
在交叉口信号相位组合方案确定的情况下，本文采用常规的信号配时模型对相位进行配时，并以车辆平均延误作为评价指标进行方案比选，选取平均延误最小的信号方案作为信号交叉口最优的控制方案.通过计算，得到所有可行相位组合方案对应的车辆平均延误如图 4所示.

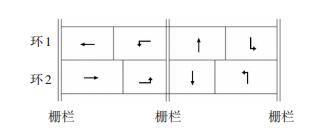
从图 4中可以发现，交叉口信号控制相位组合方案的不同，对交叉口控制效果影响显著，即不同相位组合方案，车辆平均延误相差较大，图中最小值、最大值分别为：36.326 8、73.054 68 s/pcu，最大最小车辆平均延误相差近2倍，由此说明信号相位组合的选取对信号方案控制效果影响很大，合理选择相位组合方案尤为重要.再有，在流线车辆到达恒定的情况下，相位流线组合相同，相序不同的可行相位组合方案，通过计算发现车辆平均延误相同，即控制效果相同，由此得到最优控制方案(PM)有4个，在选择交叉口最优信控方案时可任选其一.本文选定编号为321对应的相位组合方案为最优控制方案.本文算例交叉口对应的常规控制方案有分流式(DS)，组合式(CS)，以及环栅结构(RBS)的相位组合方案，分别见表 2和图 5.并通过计算可得到PM方案与常规控制方案(DS、CS和RBS)的流线最优配时和车辆平均延误值见表 3.

从表 3中可以看出所得最优控制方案的相位流线组合，完美考虑了流线搭接(即同一流线跨越多个相位时，必须保证这些相位相邻)，再者本文所提方法得到的最优控制方案相比环栅结构相位组合方案车辆平均延误减少0.3 s/pcu，相比分流式相位组合方案减少0.5 s/pcu，相比组合式相位组合方案减少4.5 s/pcu，随着交叉口车辆的通行，交叉口总延误将大大降低.由此可以说明本文所提方法能够进一步降低交叉口延误，提升交叉口控制效率.

为了进一步验证本文所提方法的可行性和有效性，采用软件VISSIM 5.30 64Bit进行算例验证.将计算得到的常规信号控制方案和PM方案对应的最优配时方案输入至仿真软件，通过设置检测器仿真得到常规信号控制方案(DS、CS、RBS)平均延误，并进行对比分析，对比结果见图 6.

仿真对比结果与本文模型计算结果相匹配，由此进一步验证了本文方法可行.

4 结论

1) 站在优化交叉口信号相位组合的角度，通过考虑流线搭接，提出了一种新的交叉口信号控制优化算法，算法能够获取更加全面的交叉口相位组合方案.

2) 算法所得最优的控制方案相比现有常规的交叉口相位组合方法，不仅包含了环栅结构的所有优点，还进一步细化了交叉口流线相容关系，并合理的采用数学计算方法确定相位组合方案时全面的考虑流线搭接.

3) 通过算法计算，真正意义上的全局最优信号控制方案能够被获取，由此进一步减少交叉口车辆的平均延误，提升信号交叉口通行效率，缓解城市交通拥堵.

4) 该算法仅考虑了机动车流线之间的相容关系，且对左转流线均采用保护相位，所以后续研究需对其进一步完善，增加行人流线，并考虑左转许可相位的设置，以提升该算法的通用性.