同步定位与建图(SLAM)[1-2]是指移动机器人在未知环境中的未知起点开始运动,通过其自身的传感器逐步地建立环境的地图,并且通过该地图对机器人自身的位置进行更新.
SLAM问题最先提出是在文献[3]中.Smith等[3]第1次采用EKF完成了一个可应用的SLAM系统.在EKF-SLAM框架中,文献[4]使用一个多维高斯分布的向量表示机器人姿态和地标位置估计.由于机器人姿态误差和地标之间的相关性被存储在向量的协方差矩阵中,EKF可以适应地图中误差存在相关的情况.但在复杂环境中,随着地标点的增多,其中的雅克比矩阵计算会变得很复杂,计算量会非常大,不利于实时计算.同时由于EKF在线性化过程中舍弃了高阶项,在处理强非线性函数时,误差会很大.针对上述问题,文献[5]提出了粒子滤波(PF)方法,但是它的计算量非常大,很难满足SLAM实时性的要求.文献[6]提出了无迹卡尔曼滤波(UKF),UKF滤波器很好地解决了移动机器人模型的非线性问题.UKF是基于UT变换的一种非线性滤波方法,它利用确定性采样策略逼近非线性分布.与EKF相比,UKF的计算复杂度不高,对于任何非线性函数都可以达到2阶近似,也不需要计算雅可比矩阵.但是,随着系统维度的增加,采样点与中心点的距离越来越远,UT变换将产生非局部取样效应[7-8],可能导致滤波数据不稳定且有可能发散.近年来,CKF被应用于SLAM中[9-11].CKF根据容积准则,选取一组权重相同的采样点,经系统非线性方程变化后,通过加权处理近似高斯分布.它与UKF思路相近,但是CKF比UKF提取采样点少,具有严格的数学理论验证,并且解决了UKF在高维系统中会出现的数值不稳定和精度降低问题.
上述传统的方法都基于观测噪声已知并且无变化的假设,而当此假设不成立时,即观测噪声未知或噪声突变时,传统SLAM算法的性能将会受到极大的影响.为了解决该问题,研究人员提出了很多改进方法,大体上有两类:一类是基于残差和新息的改进算法[12],即根据残差和新息序列的变化对观测噪声的协方差矩阵进行实时调整,使其具有自适应能力,但此种方法是要计算时间窗内所有的残差和新息序列,计算量太大,无法满足SLAM算法的实时要求,此外,这种方法假设时间窗内的噪声分布是恒定的,所以无法处理噪声突变的情况; 另一类是基于多模型的自适应算法[13],该方法把系统的真实噪声统计特性用多个并行运算的滤波器近似,这类方法需要知道传感器误差特性,同时因有多个滤波器,所以计算量比较大.近年来,基于变分贝叶斯的机器学习方法[14-18]开始应用到滤波问题上,它具有计算量低的优点.文献[19]利用线性变分贝叶斯方法对SLAM中地图特征和噪声方差进行迭代更新.
本文提出了一种基于变分贝叶斯噪声自适应容积卡尔曼滤波的SLAM算法(VB-ACKF-SALM).该算法采用基于逆Wishart分布的变分贝叶斯方法,用逆Wishart分布对观测噪声进行建模,通过变分贝叶斯非线性高斯滤波实现对SLAM中移动机器人的状态和观测噪声参数进行估计,有效地解决了在噪声未知或变化下SLAM过程中状态发散问题并且保持了较高的精度.仿真结果验证了该算法的有效性.
1 理论介绍 1.1 概率SLAM描述SLAM的本质是机器人整个路径的概率估计问题[20],在概率形式下,SLAM问题就是求解下述概率分布:
| $ p\left( {{\mathit{\boldsymbol{x}}_{\rm{k}}}\left| {{\mathit{\boldsymbol{Z}}_{0:{\rm{k}}}},{\mathit{\boldsymbol{U}}_{0:{\rm{k}}}}} \right.} \right). $ |
式中:xk=[xvk, m]T为状态向量; xvk=[xk, yk, θk]T为机器人的位姿; m=[m1, m2, …, ml]T,mi=[xi, yi]T, i=1, 2, …, l,表示所有的路标位置; 其中l为路标序号; Z0:k={z1, z2, …, zk}为直到k时刻所有的观测.U0:k={u1, u2, …, uk}为直到k时刻所有控制的变量.该分布表示的是k时刻在给定的观测和控制量下机器人的状态和路标位置的联合后验概率密度.根据贝叶斯定理可以得到:
| $ p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{Z}}_{0:k}},{\mathit{\boldsymbol{U}}_{0:k}}} \right.} \right) = \frac{{p\left( {{z_k}\left| {{x_k}} \right.} \right)p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{Z}}_{0;k - 1}},{\mathit{\boldsymbol{U}}_{0:k}}} \right.} \right)}}{{p\left( {{z_k}\left| {{\mathit{\boldsymbol{Z}}_{0;k - 1}},{\mathit{\boldsymbol{U}}_{0:k}}} \right.} \right)}}, $ |
由全概率公式和马尔科夫链可得
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{Z}}_{0:k - 1}},{\mathit{\boldsymbol{U}}_{0:k}}} \right.} \right) = \int {p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\boldsymbol{u}}_k}} \right.} \right)} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_{k - 1}}\left| {{\mathit{\boldsymbol{Z}}_{0;k - 1}},{\mathit{\boldsymbol{U}}_{0:k - 1}}} \right.} \right){\rm{d}}{\mathit{\boldsymbol{x}}_{k - 1}}. \end{array} $ |
式中:p(zk|xk)为观测似然; p(xk|xk-1, uk)为状态转移密度.
1.2 变分贝叶斯噪声自适应滤波假设k时刻的状态向量xk与观测协方差矩阵Rk是相互独立的,则有
| $ p\left( {{x_k},{\mathit{\boldsymbol{R}}_k}\left| {{x_{k - 1}}} \right.,{\mathit{\boldsymbol{R}}_{k - 1}}} \right) = p\left( {{x_k}\left| {{x_{k - 1}}} \right.} \right) \times p\left( {{\mathit{\boldsymbol{R}}_k}\left| {{\mathit{\boldsymbol{R}}_{k - 1}}} \right.} \right). $ |
通过递推变分贝叶斯算法,可以在已知前k个时刻观测量以及初始概率密度p(x0, R0)的条件下,通过预测与更新两个过程,估计出联合后验概率密度p(xk, Rk|Z1:k).在这里对符号进行说明,以状态向量为例:xk|k-1为状态的一步预测值,xk|k为更新后的值.
假设k-1时刻的xk-1, Rk-1的联合条件概率分布为高斯分布和逆Wishart分布的乘积,即
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\boldsymbol{R}}_{k - 1}}\left| {{\mathit{\boldsymbol{Z}}_{1:k - 1}}} \right.} \right) = N\left( {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\boldsymbol{P}}_{k - 1}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;IW\left( {{\mathit{\boldsymbol{R}}_{k - 1}}\left| {{v_{k - 1}},{\mathit{\boldsymbol{V}}_{k - 1}}} \right.} \right), \end{array} $ |
其中,逆Wishart分布概率密度函数为
| $ f\left( \mathit{\boldsymbol{R}} \right) = \frac{{{{\left| \mathit{\boldsymbol{V}} \right|}^{\frac{v}{2}}}}}{{{2^{\frac{m}{2}}}{\mathit{\Gamma }_n}\left( {\frac{v}{2}} \right)}}{\left| \mathit{\boldsymbol{R}} \right|^{ - \frac{{v + n + 1}}{2}}}{\mathit{\boldsymbol{e}}^{ - \frac{1}{2}{\rm{tra}}\left( {V{R^{ - 1}}} \right)}}, $ |
则预测过程为
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{R}}_k}\left| {{\mathit{\boldsymbol{Z}}_{1:k - 1}}} \right.} \right) = p\left( {{\mathit{\boldsymbol{x}}_k}\left| {{\mathit{\boldsymbol{Z}}_{1:k - 1}}} \right.} \right)p\left( {{\mathit{\boldsymbol{R}}_k}\left| {{\mathit{\boldsymbol{Z}}_{1:k - 1}}} \right.} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}},{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;IW\left( {{\mathit{\boldsymbol{R}}_{k\left| {k - 1} \right.}}\left| {{\nu _{k\left| {k - 1} \right.}},{\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}}} \right.} \right). \end{array} $ |
式中:xk|k-1、Pk|k-1分别为状态的一步预测值与其对应的误差协方差矩阵;Rk|k-1为未知观测噪声协方差矩阵的一步预测值;νk|k-1、Vk|k-1分别为逆Wishart分布参数的一步预测值.
在更新过程中,根据标准的变分贝叶斯方法,可以得到后验概率分布p(xk, Rk|Z1:k)的近似形式如下
| $ p\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{R}}_k}\left| {{\mathit{\boldsymbol{Z}}_{1:k}}} \right.} \right) \approx {q_x}\left( {{\mathit{\boldsymbol{x}}_k}} \right){q_{\rm{R}}}\left( {{\mathit{\boldsymbol{R}}_k}} \right). $ |
此时可以通过最小化真实后验分布与近似分布之间的Kullback-Leibler(KL)散度得到相关的模型参数为
| $ \begin{array}{l} {\rm{KL}}\left[ {{q_x}\left( {{\mathit{\boldsymbol{x}}_k}} \right){q_{\rm{R}}}\left( {{\mathit{\boldsymbol{R}}_k}} \right)\left\| {p\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{R}}_k}\left| {{\mathit{\boldsymbol{Z}}_{1:k}}} \right.} \right)} \right.} \right] = \\ \int {{q_x}\left( {{\mathit{\boldsymbol{x}}_k}} \right){\mathit{\boldsymbol{q}}_{\rm{R}}}\left( {{\mathit{\boldsymbol{R}}_k}} \right)} \times \log \left( {\frac{{{q_x}\left( {{\mathit{\boldsymbol{x}}_k}} \right){q_{\rm{R}}}\left( {{\mathit{\boldsymbol{R}}_k}} \right)}}{{p\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{R}}_k}\left| {{\mathit{\boldsymbol{Z}}_{1:k}}} \right.} \right)}}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_k}{\rm{d}}{\mathit{\boldsymbol{R}}_k}. \end{array} $ | (1) |
由式(1)可得qx(xk)服从高斯分布,qR(Rk)服从逆Wishart分布,即:
| $ \begin{array}{*{20}{c}} {{q_x}\left( {{\mathit{\boldsymbol{x}}_k}} \right) = N\left( {{\mathit{\boldsymbol{x}}_{k\left| k \right.}},{\mathit{\boldsymbol{P}}_{k\left| k \right.}}} \right),}\\ {{\mathit{\boldsymbol{q}}_{\rm{R}}}\left( {{\mathit{\boldsymbol{R}}_k}} \right) = IW\left( {{\mathit{\boldsymbol{R}}_{k\left| k \right.}}\left| {{\nu _{k\left| k \right.}},{\mathit{\boldsymbol{V}}_{k\left| k \right.}}} \right.} \right),} \end{array} $ |
其中:
| $ \begin{array}{l} {v_k} = {v_{k\left| {k - 1} \right.}} + 1,\\ {\mathit{\boldsymbol{V}}_{k\left| k \right.}} = {\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}} + \int {\left( {{z_k} - h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right){{\left( {{z_k} - h\left( {{x_k}} \right)} \right)}^{\rm{T}}}} \times \\ \;\;\;\;\;\;\;\;\;N\left( {{\mathit{\boldsymbol{x}}_{k\left| k \right.}},{\mathit{\boldsymbol{P}}_{k\left| k \right.}}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_k}. \end{array} $ |
由上述分析整理得到变分贝叶斯噪声估计非线性高斯滤波算法如下.
1.2.1 预测过程状态向量预测为
| $ {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}} = f\left( {{\mathit{\boldsymbol{x}}_{k - 1\left| {k - 1} \right.}}} \right). $ |
协方差矩阵预测为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}} = \int {\left( {f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) - f\left( {{\mathit{\boldsymbol{x}}_{k - 1\left| {k - 1} \right.}}} \right)} \right)\left( {f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) - } \right.} }\\ {\;\;\;\;\;\;\;\;\;\;{{\left. {f\left( {{\mathit{\boldsymbol{x}}_{k - 1\left| {k - 1} \right.}}} \right)} \right)}^{\rm{T}}}N\left( {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\boldsymbol{P}}_{k - 1}}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_{k - 1}} + {\mathit{\boldsymbol{Q}}_{k - 1}}.} \end{array} $ |
观测噪声方差阵分布参数预测为:
| $ \begin{array}{*{20}{c}} {{v_{k\left| {k - 1} \right.}} = \rho \left( {{v_{k - 1}} - n - 1} \right) + n + 1,}\\ {{\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{V}}_{k - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}.} \end{array} $ |
式中:f(·)为状态方程;ρ为(0, 1)内的变化因子,其作用是使时变的观测噪声协方差矩阵以一定的概率分布变化,目的是使后验与先验的概率密度函数形式相同;
更新过程为:
| $ \begin{array}{*{20}{c}} {{z_{k\left| {k - 1} \right.}} = h\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right),}\\ {{\mathit{\boldsymbol{P}}_{xz,k\left| {k - 1} \right.}} = \int {\left( {{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right)\left( {h\left( {{\mathit{\boldsymbol{x}}_k}} \right) - h{{\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right)}^{\rm{T}}}} \right)} \times }\\ {N\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}},{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_k},} \end{array} $ |
令:
| $ \begin{array}{l} \mathit{\boldsymbol{x}}_{k\left| k \right.}^0 = {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}},\mathit{\boldsymbol{P}}_{k\left| k \right.}^0 = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}},\\ {v_{k\left| k \right.}} = {v_{k\left| {k - 1} \right.}} + 1,\mathit{\boldsymbol{V}}_{k\left| k \right.}^0 = {\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}}. \end{array} $ |
式中:zk|k-1为观测的一步预测值;h(·)为观测方程;Pxz, k|k-1为互协方差矩阵.
1.2.3 进入循环进入循环为:
| $ \mathit{\boldsymbol{R}}_k^{\left( n \right)} = {\left( {{v_{k\left| k \right.}} - n - 1} \right)^{ - 1}}\mathit{\boldsymbol{V}}_{k\left| k \right.}^{\left( n \right)}, $ |
| $ \begin{array}{l} \mathit{\boldsymbol{P}}_{zz,k\left| {k - 1} \right.}^{\left( {n + 1} \right)} = \int {\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right) - h\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right)\left( {h\left( {{\mathit{\boldsymbol{x}}_k}} \right) - } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left. {h\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right)} \right)}^{\rm{T}}}} \right] \times N\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}},{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_k} + \mathit{\boldsymbol{R}}_k^{\left( n \right)}, \end{array} $ |
| $ \mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{P}}_{xz,k\left| {k - 1} \right.}}{\left( {{\rm{P}}_{zz,k\left| {k - 1} \right.}^{\left( {n + 1} \right)}} \right)^{ - 1}}, $ |
| $ \mathit{\boldsymbol{x}}_{k\left| k \right.}^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}} + \mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)}\left[ {{z_k} - h\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right)} \right], $ |
| $ \mathit{\boldsymbol{P}}_{k\left| k \right.}^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}} - \mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)}\mathit{\boldsymbol{P}}_{zz,k\left| {k - 1} \right.}^{\left( {n + 1} \right)}{\left( {\mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)}} \right)^{\rm{T}}}, $ |
| $ \begin{array}{l} \mathit{\boldsymbol{V}}_{k\left| k \right.}^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}} + \int {\left[ {\left( {{z_k} - h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right){{\left( {{z_k} - h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right)}^{\rm{T}}}} \right]} \times \\ \;\;\;\;\;\;\;\;\;\;\;N\left( {\mathit{\boldsymbol{x}}_{k\left| k \right.}^{\left( {n + 1} \right)},\mathit{\boldsymbol{P}}_{k\left| k \right.}^{\left( {n + 1} \right)}} \right){\rm{d}}{\mathit{\boldsymbol{x}}_k}. \end{array} $ |
式中:Pzz, k|k-1(n+1)为观测误差协方差矩阵,Kk(n+1)为卡尔曼增益.
当循环结束时,最终得到Vk|k=Vk|k(n+1),xk|k=xk|k(n+1), Pk|k=Pk|k(n+1).
2 变分贝叶斯噪声自适应CKF-SLAM算法根据容积准则,CKF用一组有相同权重的采样点,经过非线性方程变换后得到一组采样点来近似概率分布.该方法可以应用于非线性系统,以解决非线性系统模型的估计问题[21].在观测噪声协方差矩阵未知的情况下,本文可以使用变分贝叶斯自适应CKF来处理上述的SLAM问题.
假设移动机器人系统的状态方程和观测方程为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_k} = f\left( {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\boldsymbol{u}}_k}} \right) = \left[ \begin{array}{l} f\left( {{\mathit{\boldsymbol{x}}_{vk - 1}},{\mathit{\boldsymbol{u}}_k}} \right) + {\mathit{\boldsymbol{w}}_k}\\ {\mathit{\boldsymbol{m}}_{k - 1}} \end{array} \right],}\\ {{z_k} = h\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\nu _k}} \end{array} $ |
式中:wk为状态噪声,是均值为0的高斯白噪声其对应的协方差矩阵为Qk; νk为观测噪声,是均值为0的高斯白噪声,其对应的协方差矩阵为Rk.
SLAM算法由预测过程和更新过程组成.首先基于前一次的系统状态和系统输入预测系统状态和状态协方差矩阵,当路标的观测值到来时,进行更新过程以获得系统状态和状态协方差矩阵的估计值.算法过程如下.
2.1 系统初始化初始化机器人的状态向量x0,协方差矩阵P0,运动噪声协方差矩阵Q0,逆Wishart分布参数v0,V0以及机器人、传感器和其他的相关参数.
2.2 预测xk-1|k-1为k-1时刻机器人的状态向量的估计值,Pk-1|k-1为k-1时刻机器人的协方差矩阵的估计值.
Cholesky分解Pk-1|k-1如下
| $ {\mathit{\boldsymbol{P}}_{k - 1\left| {k - 1} \right.}} = {\mathit{\boldsymbol{S}}_{k - 1\left| {k - 1} \right.}}\mathit{\boldsymbol{S}}_{k - 1\left| {k - 1} \right.}^{\rm{T}}. $ |
构建容积点为
| $ {\mathit{\boldsymbol{x}}_{i,k - 1\left| {k - 1} \right.}} = {\mathit{\boldsymbol{S}}_{k - 1\left| {k - 1} \right.}}{\xi _i} + {\mathit{\boldsymbol{x}}_{k - 1\left| {k - 1} \right.}},i = 1,2, \cdots ,2n. $ |
式中:n为状态向量x的维数,ξi为相互正交的点集,
状态向量预测为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{i,k\left| {k - 1} \right.}} = f\left( {{\mathit{\boldsymbol{x}}_{i,k - 1\left| {k - 1} \right.}}} \right),}\\ {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}} = 1/2n\sum {{\mathit{\boldsymbol{x}}_{i,k\left| {k - 1} \right.}}} .} \end{array} $ |
协方差矩阵预测为
| $ \begin{array}{l} {P_{k\left| {k - 1} \right.}} = \\ 1/2n\left( {\sum\limits_{i = 1}^{2n} {\left( {{x_{i,k\left| {k - 1} \right.}} - {x_{k\left| {k - 1} \right.}}} \right){{\left( {{x_{i,k\left| {k - 1} \right.}} - {x_{k\left| {k - 1} \right.}}} \right)}^{\rm{T}}}} } \right) + {\mathit{\boldsymbol{Q}}_k}. \end{array} $ |
观测噪声方差阵分布参数预测为:
| $ \begin{array}{*{20}{c}} {{v_{k\left| {k - 1} \right.}} = \rho \left( {{v_{k - 1}} - n - 1} \right) + n + 1,}\\ {{\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{V}}_{k - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}.} \end{array} $ |
观测方程为
| $ {z_k} = h\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}. $ |
本文通过观测方程计算每个观测路标的位置,将路标与状态向量中的路标相匹配,以确定每个观测地标是现有路标还是新的地标.如果是现有路标,则开始状态更新.
2.4 更新根据数据关联获得最佳匹配路标,机器人状态进行更新.对于每一个匹配的路标点,首先,构建容积点如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{i,k\left| {k - 1} \right.}} = {\mathit{\boldsymbol{S}}_{k\left| {k - 1} \right.}}{\xi _i} + {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}},i = 1,2, \cdots ,2n,}\\ {{z_{i,k\left| {k - 1} \right.}} = h\left( {{\mathit{\boldsymbol{x}}_{i,k\left| {k - 1} \right.}}} \right),}\\ {{z_{k\left| {k - 1} \right.}} = 1/2n\left( {\sum\limits_{i = 1}^{2n} {{z_{i,k\left| {k - 1} \right.}}} } \right),} \end{array} $ |
求解互相关协方差矩阵为
| $ {\mathit{\boldsymbol{P}}_{xz}} = 1/2n\left( {\sum\limits_{i = 1}^{2n} {\left( {{\mathit{\boldsymbol{x}}_{i,k\left| {k - 1} \right.}} - {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right){{\left( {{z_{i,k\left| {k - 1} \right.}} - {z_{k\left| {k - 1} \right.}}} \right)}^{\rm{T}}}} } \right), $ |
令:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_{k\left| k \right.}^0 = {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}},\mathit{\boldsymbol{P}}_{k\left| k \right.}^0 = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}},}\\ {{v_{k\left| {k,i} \right.}} = {v_{k\left| {k - 1} \right.}} + 1,\mathit{\boldsymbol{V}}_{k\left| k \right.}^0 = {\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}},} \end{array} $ |
然后按式(2)~式(10)进行N步迭代计算.
1) 观测噪声协方差矩阵计算如下
| $ \mathit{\boldsymbol{R}}_k^{\left( n \right)} = {\left( {{v_{k\left| k \right.}} - n - 1} \right)^{ - 1}}\mathit{\boldsymbol{V}}_{k\left| k \right.}^{\left( n \right)}. $ | (2) |
2) 计算自相关协方差矩阵:
| $ \begin{array}{l} \mathit{\boldsymbol{P}}_{zz}^{\left( {n + 1} \right)} = 1/2n\left( {\sum\limits_{i = 1}^{2n} {\left( {{z_{i,k\left| {k - 1} \right.}} - {z_{k\left| {k - 1} \right.}}} \right)} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {{z_{i,k\left| {k - 1} \right.}} - {z_{k\left| {k - 1} \right.}}} \right)}^{\rm{T}}}} \right) + \mathit{\boldsymbol{R}}_k^n. \end{array} $ | (3) |
3) 卡尔曼增益如下
| $ \mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{P}}_{xz}}\mathit{\boldsymbol{P}}_{zz}^{\left( {n + 1} \right) - 1}. $ | (4) |
4) 更新机器人的状态向量和协方差矩阵.
状态向量更新为
| $ \mathit{\boldsymbol{x}}_{k\left| k \right.}^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}} + \mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)}\left[ {{z_k} - h\left( {{\mathit{\boldsymbol{x}}_{k\left| {k - 1} \right.}}} \right)} \right], $ | (5) |
协方差矩阵更新为
| $ \mathit{\boldsymbol{P}}_{k\left| k \right.}^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}} - \mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right)}\mathit{\boldsymbol{P}}_{zz}^{\left( {n + 1} \right)}\mathit{\boldsymbol{K}}_k^{\left( {n + 1} \right){\rm{T}}}. $ | (6) |
5) 参数V更新.
计算容积点为:
| $ \mathit{\boldsymbol{x}}_{i,k\left| k \right.}^{\left( {n + 1} \right)} = \mathit{\boldsymbol{S}}_{k\left| k \right.}^{\left( {n + 1} \right)}{\xi _i} + \mathit{\boldsymbol{x}}_{k\left| k \right.}^{\left( {n + 1} \right)},i = 1,2, \cdots ,2n, $ | (7) |
| $ z_{i,k\left| k \right.}^{\left( {n + 1} \right)} = h\left( {x_{i,k\left| k \right.}^{\left( {n + 1} \right)}} \right), $ | (8) |
计算互相关协方差矩阵:
| $ \mathit{\boldsymbol{T}}_k^{\left( {n + 1} \right)} = 1/2n\left( {\sum\limits_{i = 1}^{2n} {\left( {{z_k} - z_{i,k\left| k \right.}^{\left( {n + 1} \right)}} \right){{\left( {{z_k} - z_{i,k\left| k \right.}^{\left( {n + 1} \right)}} \right)}^{\rm{T}}}} } \right). $ | (9) |
| $ \mathit{\boldsymbol{V}}_{k\left| k \right.}^{\left( {n + 1} \right)} = {\mathit{\boldsymbol{V}}_{k\left| {k - 1} \right.}} + \mathit{\boldsymbol{T}}_k^{\left( {n + 1} \right)}. $ | (10) |
当循环结束时,最终得到Vk|k=Vk|k(n+1),xk|k=xk|k(n+1),Pk|k=Pk|k(n+1).
2.5 状态增广根据数据关联,获得新的地图特征点m,然后将特征位置信息扩展到状态向量,完成地图更新.
类似的,可以把新的路标加入到状态向量.新的路标位置可以由机器人位姿和观测量zk的函数g(·)得到:
| $ {\mathit{\boldsymbol{m}}_{{\rm{new}}}} = g\left( {{\mathit{\boldsymbol{x}}_{vk}},{\mathit{\boldsymbol{z}}_k}} \right). $ |
将新的路标加入到状态向量中去得到新的状态向量:
| $ \mathit{\boldsymbol{x}}_k^ + = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{vk}}}\\ \mathit{\boldsymbol{m}}\\ {g\left( {{\mathit{\boldsymbol{x}}_{vk}},{\mathit{\boldsymbol{z}}_k}} \right)} \end{array}} \right]. $ |
通过上述循环,本文可以实现基于变分贝叶斯自适应CKF算法的移动机器人SLAM.
3 实验验证与分析 3.1 系统建模本文模型参照了USYD的Bailey的SLAM模型[1],即前轮驱动并转向的车辆运动学模型,假定观测的路标点为静止.
机器人运动学模型为
| $ {\mathit{\boldsymbol{s}}_k} = f\left( {{\mathit{\boldsymbol{s}}_{k - 1}},{\mathit{\boldsymbol{u}}_k}} \right) = {\mathit{\boldsymbol{s}}_{k - 1}} + \left[ \begin{array}{l} \mathit{\boldsymbol{T}}{v_k}\cos \left( {{\theta _{k - 1}} + {\alpha _k}} \right)\\ \mathit{\boldsymbol{T}}{v_k}\sin \left( {{\theta _{k - 1}} + {\alpha _k}} \right)\\ \mathit{\boldsymbol{T}}{v_k}\sin {\alpha _k}/B\\ {\mathit{\boldsymbol{m}}_{k - 1}} \end{array} \right]. $ |
式中:输入sk-1=(xk-1, yk-1, θk-1, mk-1)T为k-1时刻状态向量,其中xk-1、yk-1、θk-1是机器人的位姿,分别为x轴、y轴的坐标和朝向;mk-1={m1, m2, …, ml}, i=1, 2, …, l,表示所有的路标位置,其中l为路标序号mi=(xi, yi), xi, yi分别为第i个地标的x轴和y轴的坐标;uk=(vk, αk)T,其中v(k)为机器人的速度,α(k)为机器人前轮转向的角度,T为传感器的采样时间;B为两轴间的轴距;输出sk为机器人新的位姿.
观测模型使用的是距离-角度传感器模型:
| $ \mathit{\boldsymbol{z}}\left( k \right) = \left[ {\begin{array}{*{20}{c}} \rho \\ \upsilon \end{array}} \right] = \left[ \begin{array}{l} \sqrt {{{\left( {{x_i} - {x_k}} \right)}^2} + {{\left( {{y_i} - {y_k}} \right)}^2}} \\ \left. {{{\tan }^{ - 1}}\frac{{{y_i} - {y_k}}}{{{x_i} - {x_k}}} - {\theta _k}} \right) \end{array} \right]. $ |
式中:输入(xi, yi)为已被观测到的第i个路标的位置;(xk, yk, θk)为机器人的位姿;输出的是机器人与观测路标之间的距离ρ,以及与机器人前进方向与路标的夹角υ.
3.2 实验仿真实验所用的环境区域是250 m×250 m的室外环境区域(假设障碍物静止不动).机器人运行路径的关键点和路标特征均人为指定,本实验设定35个关键点和17个路标特征.机器人从坐标位置(0, 0)开始逆时针沿关键点确定的轨迹运行两圈.在这种环境下,进行了两组不同条件下的试验.在观测噪声不变与观测噪声时变两种情况下进行了仿真.
3.2.1 观测噪声不变在此实验下,设置观测噪声方差真值为Rk=diag[0.010, 0.001].自适应CKF-SLAM中的参数:ρ=1.0,迭代次数i=3.对于传统SLAM算法,噪声R设置为初始值R0=diag[0.010 0, 0.000 3].分别采用EKF-SLAM、UKF-SLAM、CKF-SLAM、VB-ACKF-SLAM进行50次蒙特卡洛仿真实验,结果如图 1、2所示.
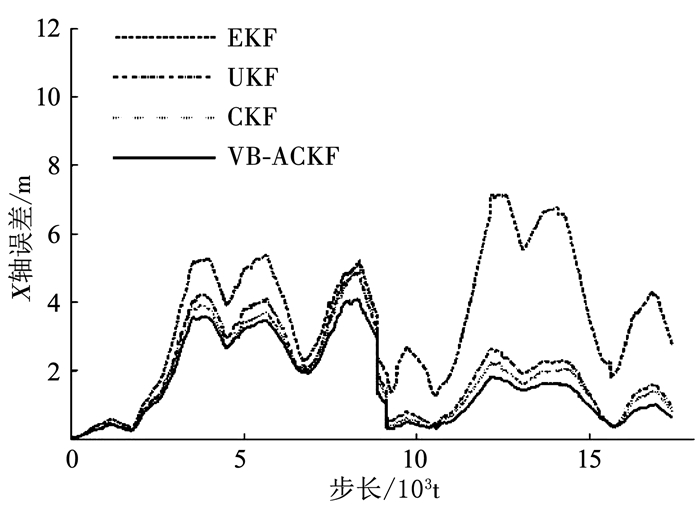
|
图 1 SLAM算法X轴误差比较 Fig. 1 X error of SLAM algorithms |
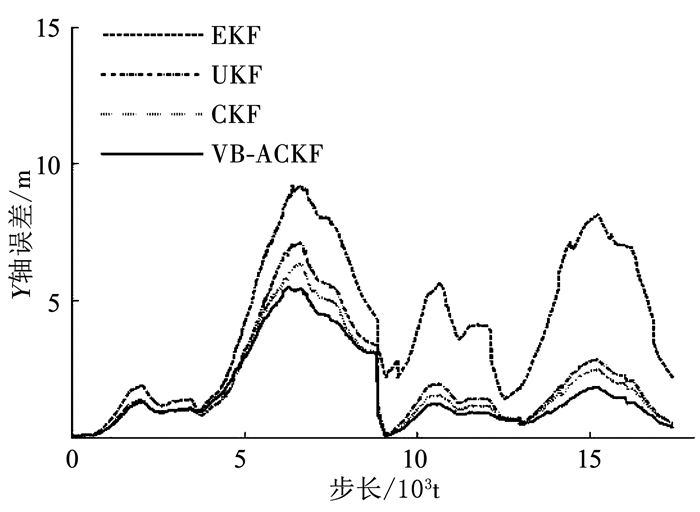
|
图 2 SLAM算法Y轴误差比较 Fig. 2 Y error of SLAM algorithms |
图 1、2分别为移动机器人位置估计在X、Y方向上的误差.横坐标t为实验的步数,每次实验都经过了17 383个时间步.由图 1、2可以看出,误差在后半段都会降低,这是因为机器人在第2圈时,再次观测到原有的路标点,进行了闭环检测提高了精度.4种算法中,EKF-SLAM误差比另外3种大很多,VB-ACKF-SLAM在X、Y方向都比UKF-SLAM,CKF-SLAM的误差要小,具有很高的精度.
表 1给出各种SLAM算法的均方根误差,进一步验证了上述的结果.
| 表 1 SLAM算法均方根误差 Tab. 1 Rmse of SLAM algorithms |
这里观测噪声设置为
| $ {\mathit{\boldsymbol{R}}_k} = \left\{ \begin{array}{l} {\rm{diag}}\left[ {0.010\;0,0.000\;3} \right],0 \le t \le 4\;000;\\ {\rm{diag}}\left[ {0.050\;0,0.001\;5} \right],4\;000 \le t < 9\;000;\\ {\rm{diag}}\left[ {{\rm{0}}{\rm{.030}}\;{\rm{0,0}}{\rm{.000}}\;{\rm{9}}} \right],9\;000 \le t < 14\;000;\\ {\rm{diag}}\left[ {0.010\;0,0.000\;3} \right],14\;000 \le t < 17\;383. \end{array} \right. $ |
同样,自适应算法设置ρ=0.90,迭代次数i=3.所有方法的噪声方差初始值设置为R=diag[0.000 1, 0.000 3].分别对EKF-SLAM,UKF-SLAM,CKF-SLAM和VB-ACKF-SLAM进行50次蒙特卡洛仿真实验.
图 3、4分别给出了移动机器人估计轨迹在X轴方向和Y轴方向上的误差.在4 000步以前,由于噪声方差没有变化,4种算法结果与观测噪声不变实验结果一致.在噪声方差发生变化后,VB-ACKF-SLAM能够同时估计噪声的方差,其精度与观测噪声不变实验基本一致,只是由于方差变大,误差稍大一点.另外3种算法因无法调整变化的观测噪声方差,一直以初始值进行计算,误差慢慢变大,在后阶段与VB-ACKF-SLAM的精度相差很大.其中EKF-SLAM甚至出现了发散的情况,无法在噪声方差变化时保持精度要求.综上分析可知,VB-ACKF-SLAM在观测噪声方差未知并且发生变化的条件下都能正常运行,并且具有很高的精度.表 2是各种SLAM算法的均方根误差.
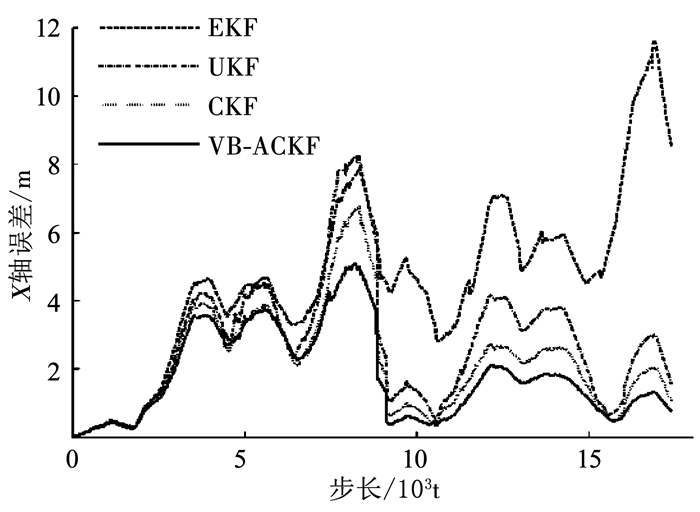
|
图 3 SLAM算法X轴误差比较 Fig. 3 X error of SLAM algorithms |
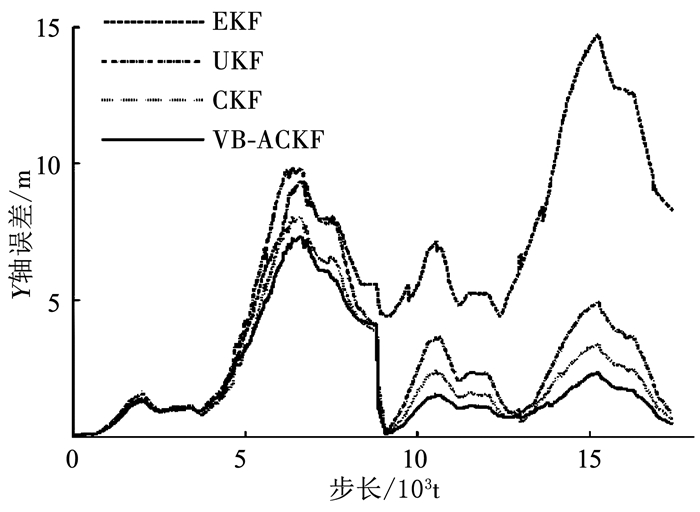
|
图 4 SLAM算法Y轴误差比较 Fig. 4 Y error of SLAM algorithms |
| 表 2 SLAM算法均方根误差 Tab. 2 Rmse of SLAM algorithms |
为了解参数ρ对算法的影响,实验中将ρ从0.60开始间隔0.05取值一直到1.00.对每个不同的参数分别在观测噪声不变和观测噪声时变的条件下对VB-ACKF-SLAM各进行50次仿真.不同参数ρ情况下的均方根误差见表 3.
| 表 3 不同参数ρ情况下的均方根误差 Tab. 3 Rmse of SLAM algorithms with different ρ |
从表 3中的结果可以知道.ρ的取值不同,会影响算法的性能.当观测噪声不变时大致呈现出ρ取值大,误差较小的趋势.当观测噪声时变时,从数据上可以得到:ρ取值在数据较大区间(0.80~1.00),误差较小;在值较小的区间,误差相对更大;但在0.90~1.00之间,随着取值越大,误差也会相对变大.当观测噪声不变的条件下,后验与先验的概率密度函数相似度高,所以当ρ较大时,算法性能较好,类似的,在观测噪声时变时,因为观测噪声是突变的,即有短时间内噪声发生变化,但在很长一段时间内是保持不变的,所以整体上后验与先验的概率密度函数相似度高,所以当ρ较大时,算法性能更好,但也有短时间变化的时刻,即后验与先验的概率密度函数相似度低,所以在ρ取0.90以上后,算法性能会有所降低.
4 结论1) 本文提出了一种基于变分贝叶斯的噪声自适应CKF-SLAM算法.在观测噪声未知或变化的情况下,该算法将观测噪声方差阵建模为逆Wishart分布,通过变分贝叶斯方法实现机器人状态和观测噪声协方差矩阵的联合估计.
2) 仿真实验结果表明, 在未知噪声时变或非时变的情况下,与传统的CKF-SLAM,UKF-SLAM和EKF-SLAM算法相比,VB-ACKF-SLAM算法具有更高的精度,这为解决未知环境中的移动机器人位置和地图创建问题提供了一个新的方法.
| [1] |
DURRANT-WHYTE H, BAILEY T. Simultaneous localization and mapping: Part Ⅰ[J]. IEEE Robotics & Amp Amp Automation Magazine, 2006, 13(2): 99. DOI:10.1109/mra.2006.1638022 |
| [2] |
CADENA C, CARLONE L, CARRILLO H, et al. Past, present, and future of simultaneous localization and mapping: toward the robust-perception age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309. DOI:10.1109/tro.2016.2624754 |
| [3] |
SMITH R, SELF M, CHEESEMAN P. Estimating uncertain spatial relationships in robotics[M]. Berlin, Heidelberg: Springer-Verlag, 1990: 435. DOI:10.1007/978-1-4613-8997-2_14
|
| [4] |
WILLIAMS B, CUMMINS M, NEIRA J, et al. A comparison of loop closing techniques in monocular SLAM[J]. Robotics & Autonomous Systems, 2009, 57(12): 1188. DOI:10.1016/j.robot.2009.06.010 |
| [5] |
MONTEMERLO M S. Fastslam: a factored solution to the simultaneous localization and mapping problem[J]. American Association for Artificial Intelligence, 2002(2): 593. |
| [6] |
SHOJAIE K, SHAHRI A M. Iterated unscented SLAM algorithm for navigation of an autonomous mobile robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice, France: IEEE, 2008: 1582. DOI: 10.1109/iros.2008.4650915
|
| [7] |
JULIER S, UHLMANN J, DURRANT-WHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477. DOI:10.1109/9.847726 |
| [8] |
YAN Xuejun, ZHAO Chunxia, XIAO Jizhong. A novel Fast SLAM algorithm based on iterated unscented Kalman filter[J]. Application Research of Computers, 2012, 31(1): 1906. DOI:10.1109/robio.2011.6181569 |
| [9] |
CHANDRA K P B, GU Dawei, POSTLETHWAITE I. Cubature Kalman filter based localization and mapping[J]. IFAC Proceedings Volumes, 2011, 44(1): 2121. DOI:10.3182/20110828-6-it-1002.03104 |
| [10] |
ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254. DOI:10.1109/tac.2009.2019800 |
| [11] |
XIA Jianzhong, IQBAL U, NOURELDIN A, et al. Adaptive square-root CKF based SLAM algorithm for indoor UGVs[C]//IEEE International Conference on Mechatronics and Automation. Takamatsu, Japan: IEEE, 2017: 1942. DOI: 10.1109/icma.2017.8016115
|
| [12] |
张文玲, 朱明清, 陈宗海. 基于强跟踪UKF的自适应SLAM算法[J]. 机器人, 2010, 32(2): 190. ZHANG Wenling, ZHU Mingqing, CHEN Zonghai. An adaptive SLAM algorithm based on strong tracking UKF[J]. Robot, 2010, 32(2): 190. DOI:10.3724/sp.j.1218.2010.00190 |
| [13] |
李晓理, 胡广大. 基于多模型方法的自适应卡尔曼滤波[J]. 系统仿真学报, 2008, 20(3): 590. LI Xiaoli, HU Guangda. Adaptive Kalman filter based on multiple model method[J]. Journal of System Simulation, 2008, 20(3): 590. |
| [14] |
SARKKA S, NUMMENMAA A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596. DOI:10.1109/tac.2008.2008348 |
| [15] |
SARKKA S, HARTIKAINEN J. Non-linear noise adaptive Kalman filtering via variational Bayes[C]//IEEE International Workshop on Machine Learning for Signal Processing. Southampton, UK: IEEE, 2013: 1. DOI: 10.1109/mlsp.2013.6661935
|
| [16] |
AIT-EL-FQUIH B, RODET T. Variational Bayesian Kalman filtering in dynamical tomography[C]//IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Prague, Czech Republic: IEEE, 2011, 4004. DOI: 10.1109/icassp.2011.5947230
|
| [17] |
DONG Peng, JING Zhongliang, HENRY L, et al. Variational Bayesian adaptive cubature information filter based on Wishart distribution[J]. IEEE Transactions on Automatic Control, 2017, 62(11): 6051. DOI:10.1109/tac.2017.2704442 |
| [18] |
SHEN Kai, JING Zhongliang, DONG Peng. A consensus nonlinear filterwith measurement uncertainty in distributed sensor networks[J]. IEEE Signal Processing Letters, 2017, 24(11): 1631. DOI:10.1109/lsp.2017.2751611 |
| [19] |
徐巍军.基于贝叶斯滤波器的移动机器人同时定位与地图创建算法研究[D].杭州: 浙江大学, 2016 XU Weijun. Research on Bayesian filters based simultaneous localization and mapping algorithms for mobile robots[D].Hangzhou: Zhejiang University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10335-1017178202.htm |
| [20] |
BARFOOT T D. State estimation for robotics[M]. Cambridge: Cambridge University Press, 2017.
|
| [21] |
沈锋, 徐广辉, 桑靖. 一种自适应变分贝叶斯容积卡尔曼滤波方法[J]. 电机与控制学报, 2015, Vol. 19(4): 94. SHEN Feng, XU Guanghui, SANG Jing. Adaptive variational Bayesian cubature Kalman filtering[J]. Electric Machines and Control, 2015, Vol. 19(No.4): 94-99. DOI:10.15938/j.emc.2015.04.015 |
 2019, Vol. 51
2019, Vol. 51


