目前，HSPF模型在流域水文水质模拟方面得到了较为广泛的应用.然而由于HSPF模型参数多，参数间交互作用机制复杂，如何获得模型优化或满意的参数集成为模型成功应用的关键问题^[1-4].由于HSPF模型参数较多，识别模型参数的灵敏度成为模型参数校准的前提.首先，一些学者对HSPF模型灵敏参数识别开展了研究^[5-11]，为后续HSPF模型参数灵敏度分析提供了重要参考.其次，在HSPF模型参数优化校准方面，程晓光和高伟等采用人工率定与PEST自动率定相结合的方法，分别对北京妨水河流域和中和流域HSPF参数进行了优化^[12-13].杨博等采用多目标率定方法，且将日径流偏差划分为丰、枯水期，提高了晋江山美水库流域HSPF模型的径流模拟效果^[14].李金城等采用PEST校准程序，以日流量偏差、月流量偏差和超流量天数为三个目标函数，将它们与实测值的加权误差作为自动校准的总目标函数，提高了牛栏江上游流域HSPF模型的径流模拟效果^[15].在上述研究的基础上，刘兴坡等应用可同时进行灵敏度分析和参数校准的实验设计方法-正交极差分析方法对青龙河流域HSPF模型进行了灵敏度分析和参数优化^[16].由于将正交实验设计方法和PEST优化有效结合，很好地协调了全局优化，避免陷入局部最优和局部优化改善优化效率的关系，合理地平衡了计算简便性以及模拟结果的精确性，该方法取得了较好的模拟效率和效果.有鉴于实验设计方法与PEST优化耦合思路的有效性，本文针对另外一种实验设计方法，即响应面优化法开展模型参数校准的实验研究，以期进一步改善青龙河流域HSPF模型参数校准效率和效果.响应面优化方法具有如下特点：1)考虑了参数随机性以及模型随机误差；2)响应面优化法将复杂未知的函数关系在小区域内采用一次或二次多项式模型来拟合，计算简便有效；3)响应面优化法可获得连续型回归模型，在参数寻优过程中，可以连续地对参数的各个水平进行分析，为此本文研究将其与正交极差分析法进行比较，评估其效率、效果和适用性，为HSPF模型参数校准提供新途径.

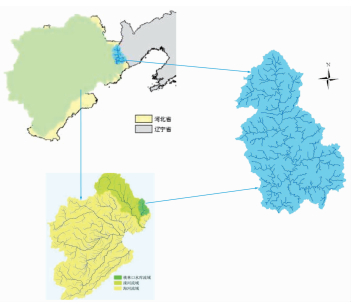
青龙河流域主体位于河北省秦皇岛市境内，流域面积6 340 km²，其下游桃林口水库为北戴河供水水源地，水质安全保障要求高.上游农业污染和农村生活污染等面源污染是流域水环境的主要风险源，点源污染影响相对较小.流域位置见图 1所示.

Fig. 1

图 1 青龙河流域地理位置 Fig. 1 Location of Qinglong River watershed

HSPF模型是当前应用广泛的半分布式流域水文水质模型，源于美国环保署1980年开发的斯坦福模型(SWM).HSPF模型包括透水地段水文水质模块PERLND、不透水地段水文水质模拟模块IMPLND以及地表水体水文水质模拟模块RCHRES等3个主要模块，适用于综合模拟流域的径流、土壤流失、河道水力和污染物迁移转化等过程，以及气候变化与土地利用变化影响下的流域水文、水环境效应模拟.其主要边界条件包括逐日降雨、气压、气温、相对湿度、蒸发、日照等数据.地形数据、土地利用数据、气象数据和水文水质数据与文献[16]相同，不再赘述.

借鉴参考文献[16-17]初步确定需要重点研究的HSPF模型参数，然后根据BASINs/HSPF的PEST参数自动校准程序初步计算上述模型参数的灵敏度，最终遴选9个模型参数作为研究对象.遴选参数的物理意义及取值范围参见表 1.

表 1

表 1 HSPF模型参数范围 Tab. 1 Parameter ranges of HSPF model 参数名称 参数意义 单位 取值范围 LZSN 土壤下层额定存储量 inch 2.0~15.0 INFILT 土壤下渗系数 inch/h 0.001~0.500 AGWRC 地下水消退系数 1/day 0.85~1.00 DEEPFR 水分下渗到承压层的比率 — 0.001~0.500 BASETP 基流蒸发系数 — 0.001~0.200 AGWETP 潜水蒸发系数 — 0.001~0.200 CEPSC 植被截留系数 — 0.01~0.40 UZSN 土壤上层额定存储量 inch 0.05~2.00 IRC 壤中流消退系数 1/day 0.30~0.85

表 1 HSPF模型参数范围 Tab. 1 Parameter ranges of HSPF model

本文应用响应面优化方法来实现HSPF模型灵敏参数的识别及其优化.响应面优化又称为响应曲面法Response Surface Optimization，是应用合理的实验设计方法和多元二次回归模型来拟合待优化参数因变量及其响应值应变量之间的函数关系，通过对回归方程的方差分析以及响应面和等高线的绘制来获得最优参数，是解决多变量优化问题的重要方法.在响应面回归分析中，响应值和待优化参数之间的数量关系y=f(x₁, x₂, …, x_n)+ε.式中，y表示响应值，x表示待优化参数，f表示代表函数关系，ε表示是误差项.响应面优化首先要获得回归方程，然后通过合理的参数设计，获得最佳响应值.本文应用响应面实验设计软件Design Expert10来实现响应面优化，包括参数设计Design、回归分析Analysis和参数优化Optimization等3个步骤.其中，响应面设计选用Box-Behnken Design(BBD)设计^[18].以9个待优化参数作为因变量，每组参数集在HSPF模型中模拟获得的NSE值作为应变量，然后通过构建应变量和因变量之间的响应面，获得参数优化区间和优化取值.

本文将响应面优化法的参数优化结果与正交极差分析法的研究结果进行比较，以论证结果合理性和可靠性.正交极差分析法将正交试验选择的各种水平组合列成正交表，通过正交表的设计和选取来安排试验方案.首先，根据参数数量和每个参数取值个数选择正交表，获得正交参数集，并输入HSPF模型进行模拟，获得NSE值、各参数各水平的实验指标之和以及单参数各水平的实验指标之和.然后，应用极差分析法进行参数灵敏度计算、优化水平评价以及确定最优参数组合.

目前，HSPF模型参数优化效果的主要评价指标包括均方误差RMSE、平均相对误差MRE、相关系数Correlation coefficient、一致性指数d和NSE模型有效性系数等.由于NSE模型有效性系数较其他指标更为严格，故此处择其作为HSPF模型参数优化效果的评价指标.

按照HSPF模型参数范围参见表 1，将各待优化参数的名称、取值范围以及参数初始值输入到Design Expert10，作为响应面分析的因变量.将上述参数集输入到HSPF模型，可获得模拟曲线结果，计算模拟径流时间序列和实测径流时间序列的NSE值.

将各组参数集运行获得的NSE值输入到Design Expert10的Response列，作为响应面分析的应变量；运行Design Expert10软件，可获得N组参数集和N个NSE值，构成响应面分析的N组应变量-因变量组合(本文为130组).在Design Expert10软件的Analysis功能Model选项中选取2FI考虑两个参数的交互影响，可获得回归方差分析表以及各个待优化参数的p值(p值代表了各参数的显著性水平).若参数的p < 0.05，则判定该参数为灵敏参数.应用响应面设计软件Design Expert10中的等高线和3D-Surface功能获得等高线和响应面，从而分析各参数对响应值的影响、影响的显著区域以及各因素的交互作用，从而获得各待优化参数在NSE最大取值时的取值范围.应用响应面设计软件Design Expert10，将获得的参数取值范围再次输入到Design Expert10软件中Optimization功能的Numerical命令中，可以获得上述待优化参数的最优取值.

为了保证上述方法可靠性，针对回归方差分析表中获得的高灵敏参数进行再次的深度寻优，重复上述步骤，获得进一步结论，并与正交极差分析、PEST自动校准等结果进行比较分析.

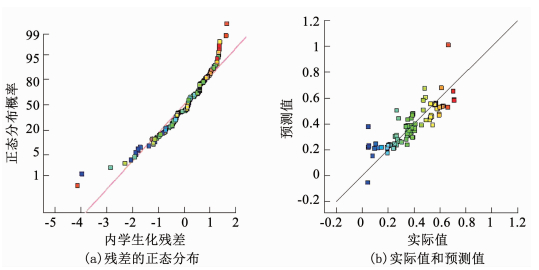
应用Design-Expert10软件对上述遴选的9个参数进行回归方差分析和灵敏度检验，发现构建的响应面优化模型p值小于0.000 1远远小于0.050 0，这表明该模型极灵敏且该模型在被研究的回归区域拟合性能很好，模型残差满足正态分布，见图 2所示.参见表 2，可以发现HSPF模型参数LZSN、INFILT和AGWRC是极灵敏参数，DEEPFR是灵敏参数，其他5个参数则不灵敏.同时，发现AB(LZSN和INFILT)、BC(INFILT和AGWRC)、BH(INFILT和UZSN)和BJ(INFILT和IRC)等参数的两两交互作用对模拟结果的影响灵敏.

Fig. 2

图 2 回归模型残差正态分布以及预测值和实际值关系 Fig. 2 Normal distribution of residual error and comparison between the predicted value and the actual value of regression model

表 2

表 2 响应面回归模型方差分析结果 Tab. 2 Variance analysis results of response surface regression analysis 参数及参数组合 平方和 统计自由度 回归均方差 F值 P值 灵敏度 回归模型 2.31 45 0.062 4.87 < 0.000 1 极灵敏 A(LZSN) 0.75 1 0.75 58.99 < 0.000 1 极灵敏 B(INFILT) 0.29 1 0.29 22.81 < 0.000 1 极灵敏 C(AGWRC) 1.07 1 1.07 84.04 < 0.000 1 极灵敏 D(DEEPFR) 0.18 1 0.18 13.79 0.000 4 灵敏 E(BASETP) 1.960×10-3 1 1.960×10-3 0.15 0.695 7 不灵敏 F(AGWETP) 4.225×10-6 1 4.225×10-6 3.320×10-4 0.985 5 不灵敏 G(CEPSC) 4.422×10-4 1 4.422×10-4 0.035 0.852 6 不灵敏 H(UZSN) 0.018 1 0.018 1.41 0.239 1 不灵敏 J(IRC) 2.970×10-4 1 2.970×10-4 0.023 0.878 9 不灵敏 AB 0.17 1 0.17 13.06 0.0005 灵敏 AC 5.512×10-5 1 5.512×10-5 4.331×10-3 0.947 7 不灵敏 AD 1.369×10-3 1 1.369×10-3 0.11 0.743 8 不灵敏 AE 2.205×10-4 1 2.205×10-4 0.017 0.895 6 不灵敏 AF 6.125×10-6 1 6.125×10-6 4.812×10-4 0.982 5 不灵敏 AG 4.441×10-16 1 4.441×10-16 3.489×10-14 1.000 0 不灵敏 AH 3.486×10-3 1 3.486×10-3 0.27 0.602 1 不灵敏 AJ 3.125×10-4 1 3.125×10-4 0.025 0.875 9 不灵敏 BC 0.060 1 0.060 4.72 0.032 7 灵敏 BD 0.019 1 0.019 1.50 0.223 9 不灵敏 BE 1.891×10-4 1 1.891×10-4 0.015 0.903 3 不灵敏 BF 4.513×10-5 1 4.513×10-5 3.546×10-3 0.952 7 不灵敏 BG 1.513×10-5 1 1.513×10-5 1.188×10-3 0.972 6 不灵敏 BH 0.15 1 0.15 11.69 0.001 0 灵敏 BJ 0.051 1 0.051 3.99 0.049 1 灵敏 CD 0.016 1 0.016 1.26 0.265 1 不灵敏 CE 7.200×10-5 1 7.200×10-5 5.657×10-3 0.940 2 不灵敏 CF 0.000 1 0.000 0.000 1.000 0 不灵敏 CG 4.441×10-16 1 4.441×10-16 3.489×10-14 1.000 0 不灵敏 CH 4.050×10-3 1 4.050×10-3 0.32 0.574 2 不灵敏 CJ 3.610×10-4 1 3.610×10-4 0.028 0.866 7 不灵敏 DE 5.281×10-4 1 5.281×10-4 0.041 0.839 1 不灵敏 DF 9.112×10-5 1 9.11210-5 7.160×10-3 0.932 8 不灵敏 DG 4.441×10-16 1 4.441×10-16 3.489×10-14 1.000 0 不灵敏 DH 9.680×10-4 1 9.680×10-4 0.076 0.783 4 不灵敏 DJ 6.125×10-6 1 6.125×10-6 4.812×10-4 0.982 5 不灵敏 EF 1.361×10-4 1 1.361×10-4 0.011 0.917 9 不灵敏 EG 8.882×10-16 1 8.882×10-16 6.979×10-14 1.000 0 不灵敏 EH 5.062×10-6 1 5.062×10-6 3.978×10-4 0.984 1 不灵敏 EJ 5.000×10-7 1 5.000×10-7 3.929×10-5 0.995 0 不灵敏 FG 1.512×10-5 1 1.512×10-5 1.188×10-3 0.972 6 不灵敏 FH 3.125×10-6 1 3.125×10-6 2.455×10-4 0.987 5 不灵敏 FJ 1.000×10-6 1 1.000×10-6 7.857×10-5 0.992 9 不灵敏 GH 2.592×10-3 1 2.592×10-3 0.20 0.652 9 不灵敏 GJ 2.592×10-3 1 2.592×10-3 0.20 0.652 9 不灵敏 HJ 3.042×10-3 1 3.042×10-3 0.24 0.626 2 不灵敏 注：(1)表中AB代表参数LZSN(A)与参数INFILT(B)的交互作用，其他类似；(2)F值检验设为95%置信，小于0.05的p值即判定为置信.

表 2 响应面回归模型方差分析结果 Tab. 2 Variance analysis results of response surface regression analysis

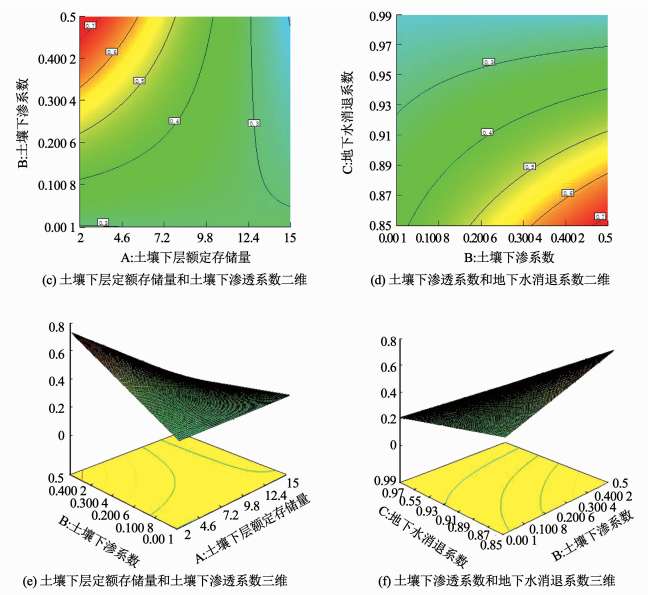
见图 3所示的等高线二维图和三维图，可直观分析NSE值最大时各参数之间交互作用对模拟结果的灵敏程度和各参数的满意取值范围.通过响应面设计Design Expert10软件的Optimization>Numerical>Solutions功能可获得参数优化的取值方案.表 3列出了各参数的优化取值：LZSN=2.088，INFILT=0.499，AGWRC=0.871，DEEPFR=0.113，BASETP=0.101，AGWETP=0.088，CEPSC=0.199，UZSN=1.020，IRC=0.551.

Fig. 3

图 3 HSPF参数及其交互作用响应面 Fig. 3 Response surface of HSPF parameters and their interactions

表 3

表 3 响应面优化法一次寻优参数取值 Tab. 3 One-stage optimization parameters of the response surface optimization method 参数名称 最小取值 最大取值 最优参数 LZSN 2 4.6 2.088 INFILT 0.400 2 0.5 0.499 AGWRC 0.87 0.89 0.871 DEEPFR 0.100 8 0.200 6 0.113 BASETP 0.080 6 0.120 4 0.101 AGWETP 0.080 6 0.120 4 0.088 CEPSC 0.166 0.244 0.199 UZSN 0.83 1.22 1.020 IRC 0.52 0.63 0.551

表 3 响应面优化法一次寻优参数取值 Tab. 3 One-stage optimization parameters of the response surface optimization method

为验证响应面优化方法的有效性，将响应面一次寻优获得的4个灵敏参数再次寻优，其余5个参数保持不变.将一次寻优获得的参数取值范围再次输入到Design Expert10软件，获得29组参数集，模拟方法和一次寻优相似，此处不再考虑参数之间的交互影响，即将2FI改变为Linear，从而获得4个灵敏参数的二次寻优值，见表 4所示.综合响应面优化法的一次寻优和二次寻优结果，可以获得9个HSPF模型参数的密集区间和最优推荐值，见表 5.

表 4

表 4 响应面一次寻优和二次寻优参数取值范围比较 Tab. 4 Comparison of one-stage and two-stage parameter intervals of the response surface optimization method 参数名称 一次寻优取值区间 二次寻优取值区间 二次寻优值 LZSN [2.0, 4.6] [2.00, 2.65] 2.000 INFILT [0.400 2, 0.5] [0.400, 0.475] 0.400 AGWRC [0.87, 0.89] [0.870, 0.885] 0.870 DEEPFR [0.100 8, 0.200 6] [0.101, 0.176] 0.101

表 4 响应面一次寻优和二次寻优参数取值范围比较 Tab. 4 Comparison of one-stage and two-stage parameter intervals of the response surface optimization method

表 5

表 5 响应面优化法二次寻优参数取值和密集取值区间 Tab. 5 Optimal parameter values and dense intervals of the response surface optimization method after two-stage optimization 参数名称 当前最优取值 密集取值区间 LZSN 2.000 [2.00, 2.65] INFILT 0.400 [0.400, 0.475] AGWRC 0.870 [0.870, 0.885] DEEPFR 0.101 [0.101, 0.176] BASETP 0.101 [0.001, 0.120] AGWETP 0.088 [0.083, 0.120] CEPSC 0.199 [0.166, 0.244] UZSN 1.020 [0.830, 1.220] IRC 0.551 [0.530, 0.630]

表 5 响应面优化法二次寻优参数取值和密集取值区间 Tab. 5 Optimal parameter values and dense intervals of the response surface optimization method after two-stage optimization

为验证响应面优化法的可靠性，与正交极差分析方法进行比较分析.参见表 6可知，响应面设计的130组所得到的NSE系数的平均值、最大值、最小值均高于文献[16]所应用的正交极差分析法.

表 6

表 6 响应面优化与正交极差分析的优化结果比较 Tab. 6 Comparison of optimization results between orthogonal range analysis and response surface — 正交极差二次寻优 响应面二次寻优 NSE平均值 0.52 0.59 NSE最大值 0.79 0.86 NSE最小值 0.01 0.10

表 6 响应面优化与正交极差分析的优化结果比较 Tab. 6 Comparison of optimization results between orthogonal range analysis and response surface

为比较响应面优化法与正交极差分析法的效率，比较两种方法获得的参数密集区间与原始参数取值区间的不同.参见表 7可知，响应面优化法的寻优区间缩减率平均值为79.82%，而正交极差分析方法的效率平均值为64.03%，由此可见，响应面优化法在参数寻优区间方面的总体效率比正交极差分析法为高.

表 7

表 7 响应面优化法与正交极差分析法的HSPF参数密集区间比较 Tab. 7 Comparison of HSPF parameter dense intervals between response surface optimization method and orthogonal range analysis method 参数名称 正交极差分析法 响应面优化法 原始取值区间 密集区间 区间缩减率% 密集区间 区间缩减率% LZSN [2.0, 6.3] 66.92 [2.00, 2.65] 95.00 [2, 15] INFILT [0.084, 0.167] 83.37 [0.400, 0.475] 84.97 [0.001, 0.500] AGWRC [0.90, 0.95] 66.67 [0.870, 0.885] 90.00 [0.85, 1.00] DEEPFR [0.209, 0.333] 75.15 [0.101, 0.176] 84.97 [0.001, 0.500] BASETP [0.067, 0.199] 33.67 [0.001, 0.120] 40.20 [0.001, 0.200] AGWETP [0.067, 0.199] 33.67 [0.083, 0.120] 81.41 [0.001, 0.200] CEPSC [0.14, 0.27] 66.67 [0.166, 0.244] 80.00 [0.01, 0.40] UZSN [1.35, 2.00] 66.67 [0.83, 1.22] 80.00 [0.05, 2.00] IRC [0.392, 0.483] 83.45 [0.53, 0.63] 81.82 [0.30, 0.85]

表 7 响应面优化法与正交极差分析法的HSPF参数密集区间比较 Tab. 7 Comparison of HSPF parameter dense intervals between response surface optimization method and orthogonal range analysis method

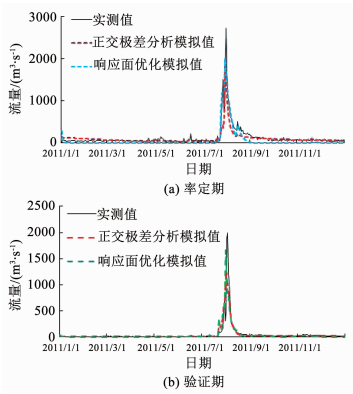
将两次响应面优化方法获得的参数集输入HSPF模型检验其水文模块的实际模拟效果.以2012年为率定期，2011年为验证期，率定期2011到2012年NSE值为0.86，验证期2011年NSE值为0.87，这表明响应面优化方法获得的参数集可较好满足水文模拟要求，见图 4所示.而PEST自动校准获得参数集的NSE值为0.84以及正交极差分析获得的参数集的NSE值为0.79^[16]，这表明响应面优化法获得的参数优于上述两种方法.

Fig. 4

图 4 桃林口水库流量监测值与模拟值比较 Fig. 4 Comparison of the measured flow in Taolinkou Reservoir and the simulated flow

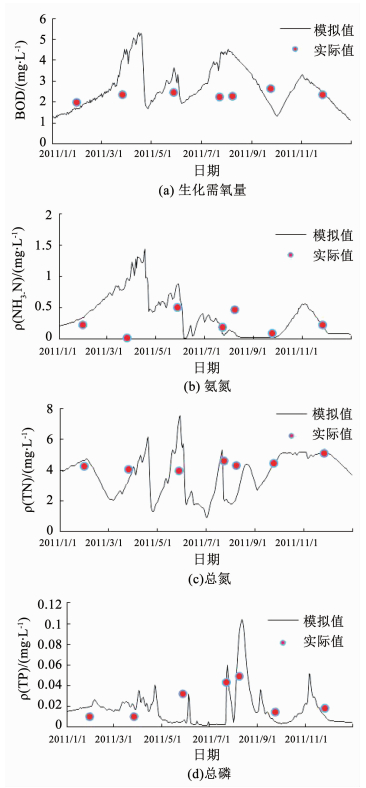
在径流参数校准的基础上，初步对BOD、NH₃-N、TN、TP等四个水质指标进行了模拟，模拟结果见图 5所示.根据模拟值与实测值的比较，TP和TN指标的模拟值与监测值吻合度较好，而BOD和NH₃-N尚存一定不确定性.由于水质模拟是在水文径流模拟、泥沙模拟和水温模拟的基础上进行的，因此泥沙模拟、水温模拟和水质过程参数获取是提高水质模拟效果的关键.

Fig. 5

图 5 桃林口水库各水质指标模拟值与实测值比较 Fig. 5 Comparison of the simulated values and the measured values of water quality indicators in Taolinkou reservoir

本文针对青龙河流域HSPF模型，遴选9个模型参数LZSN、UZSN、INFILT、IRC、BASETP、AGWETP、AGWRC、CEPSC、DEEPFR，应用响应面优化法进行参数寻优和可靠性分析，获得以下结论：

1) BASINs/HSPF模型参数的响应面优化方法在优化效果和效率方面均优于PEST参数自动校准

以及正交极差联合分析法，比正交极差联合分析方法更为高效；

2) 响应面优化方法可以分析HSPF模型参数的交互作用.本文研究表明，LZSN和INFILT、INFILT和AGWRC、INFILT和IRC、INFILT和UZSN等参数的交互作用对模型模拟结果的影响较为显著.

3) 针对青龙河流域HSPF模型，应用响应面优化方法识别出4个高灵敏的HSPF模型参数LZSN、INFILT、AGWRC、DEEPFR，与正交极差分析方法的研究结果一致；

4) 应用响应面优化方法获得HSPF模型参数优化取值区间依次为：LZSN[2.00, 2.65]；INFILT[0.400, 0.475]；AGWRC[0.870, 0.885]；DEEPFR[0.101, 0.176]；BASETP[0.001, 0.120]；AGWETP[0, 083, 0.120]；CEPSC[0.166, 0.244]；UZSN[0.83, 1.22]；IRC[0.53, 0.63].