2. 金属矿山高效开采与安全教育部重点实验室(北京科技大学), 北京 100083
2. Key Lab of High- Efficient Mining and Safety of Metal Mines (University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China
脆性是岩体在很小塑性变形下就发生破坏的性质,同时脆性破坏过程中伴随着弹性应变能的释放.作为岩体的重要基本特性,脆性评价对于油气田开采领域储层改造、地下巷道与硐室围岩稳定以及岩爆灾害预测等方面具有重要指导意义[1].现阶段,国内外许多学者对脆性指标评价作了大量研究(见表 1),但关于岩石脆性指标定义及测试方法却没有统一标准.一些学者基于应力-应变曲线研究脆性指标.文献[2]把应力-应变曲线中峰值前后能量比值转化为弹模比值,提出了脆性指标B1和B2;文献[3]在脆性破坏机制基础上,基于应力-应变曲线定义了页岩脆性指标B3;文献[4]在应力-应变曲线峰后应力降的相对大小和绝对速率基础上,提出一种能够考虑岩石塑性屈服特性和应力状态的新指标B4,并通过单轴和三轴压缩试验对B4进行了验证;文献[1]采用峰后应力跌落速率及失稳破坏时所释放弹性能与峰前储存的总能量比值定义了脆性指标B5;文献[5]综合考虑峰后应力跌落速率及起裂应力值至峰值强度值之间的应力增长速率,建立了脆性指标B6;文献[6]引入了仅涉及材料峰后行为的脆性指标B7;文献[7]在文献[6]的研究基础上考虑了峰值前后阶段速率的变化,从应变角度出发,根据塑性理论提出了脆性指标B8;文献[8]从加载过程中应变和应变能角度出发,提出了脆性指标B9和B10;文献[9-10]基于应力-应变曲线分别从能量和应变角度提出了B11和B12.另外,一些学者基于拉压强度研究脆性指标.文献[11]研究了渗透率与脆性指标之间的关系,在统计分析拉压强度试验数据中总结了四种不同的脆性指标B13~B16,并获得脆性指标与渗透率和标准化渗透率之间的关系;文献[12]在文献[11]的研究基础上探讨了脆性指标与起裂应力水平之间的函数关系,并重新定义了B13~B16.还有一些学者根据测试方法(莫尔圆[8-9]、矿物组分[13]、硬度测试[14-15]、冲击试验[16-17]、贯入试验[18-19]、弹性性质[13]、破裂角[2]、断裂试验[20])的不同提出脆性指标.虽然上述脆性指标的研究十分丰富并取得大量成果,但是针对拉压强度的脆性指标与能量之间关系的研究鲜有报道.
| 表 1 国内外岩石脆性指标汇总 Tab. 1 Summary of brittleness indexes at home and abroad |
本文从能量角度和硬岩渐进破坏过程中的变形破裂出发,总结分析了现阶段岩石起裂应力多种确定方法的优缺点,在单轴压缩试验基础上选用侧向应变差法确定了岩石试样的起裂应力,根据岩石断裂力学理论和能量理论分析了脆性指标与弹性应变能(起裂弹性应变能和峰值弹性应变能)存在的内在联系,基于两种岩石单轴压缩试验数据,利用拟合公式建立了脆性指标B13、B14、B15和B16与弹性应变能之间的函数关系,并重新定义了B13、B14、B15和B16指标.通过本文的研究,为岩石脆性指标与弹性应变能关系的确定提供了一种新思路.
1 硬岩起裂应力确定方法概述岩石中存在着大量细观缺陷,在应力集中作用下易萌生出微裂纹,进而扩展连通形成宏观破裂面.微裂纹萌生和起裂可看作是岩石渐进破坏过程的起点.本节将详细探讨室内试验岩石试样渐进破坏过程中裂纹起裂应力的确定方法.
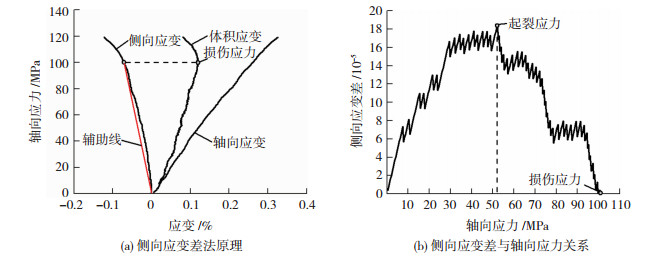
目前,确定起裂应力的方法大体有:体积应变法[21]、侧向应变法[22]、裂纹体积应变法[23]、侧向应变差法[24]、声发射法[25]和数值模拟法[26].体积应变法是通过轴向应力-体积应变曲线中的线性段末点确定岩石的起裂应力,该方法优点是确定岩石起裂应力较为直观,简便和易操作,缺点是依赖于人为做切线,存在无法避免的主观性和取值误差;侧向应变法使用轴向应力-侧向应变曲线中偏离线性的拐点来确定起裂应力,该方法具有体积应变法的优点,并去除了轴向应变的影响,干扰因素少,缺点同体积应变法;裂纹体积应变法通过计算岩石压缩过程中总体积应变与弹性体积应变的差值获得裂纹体积应变,当裂纹体积应变的绝对值大于0,微裂纹起裂开始,起裂应力通过裂纹体积应变-轴向应变曲线确定,该方法优点是不再采用人为做切线确定起裂应力,确定起裂点的过程中避免了与裂隙闭合点混淆,得出的起裂应力值相对客观,缺点是依赖于弹性模量和泊松比的计算,对泊松比的变化比较敏感,判断起裂点偏离零点也易产生误差;侧向应变差法是在轴向应力-体积应变曲线中确定损伤应力,通过连接原点与损伤应力形成一条辅助线,并确定辅助线上对应的侧向应变值,将实测侧向应变减去辅助侧向应变即为侧向应变差,最后作出侧向应变差与轴向应力关系图,图中峰值点即为起裂应力,该方法优点是极值的确定具有惟一性,避免了人为误差,保证了结果的客观性;缺点是仅适用于硬岩;声发射法是通过声发射系统监测岩石内部出现明显的声发射行为时对应的应力值即为起裂应力,该方法优点是常规应变方法的重要补充,缺点是声发射信号易受噪声干扰,且岩石在裂隙闭合和线弹性阶段也可能出现波动较强的声发射信号,从而干扰了对起裂应力的准确识别;数值模拟法是通过模拟绘制裂隙数量-轴向应变曲线,在该曲线中,随着应变增加,获取曲线首次出现拐点所对应的应变值,根据此应变值在应力-应变曲线中确定起裂应力,该方法优点是避免了人为误差,通过模拟方便快捷的确定起裂应力,缺点是模拟结果需要试验进行验证.综上所述,通过对比各种方法的优缺点,本文选用侧向应变差法确定三山岛花岗岩和天湖花岗闪长岩的起裂应力.
2 脆性指标与弹性应变能关系分析对于岩石的变形和破坏,从能量角度分析可知:外力对岩石做功产生不可恢复的塑性变形,在岩石内部存储弹性应变能,同时外力作用下岩石内部裂隙产生、扩展、贯通发展都将消耗能量.当岩石积蓄的弹性应变能达到一定阈值时,便释放转化成耗散能导致岩石破坏.假设试验系统是一个密闭系统,试验过程中能量交换仅存在于岩石试样与试验机之间,与外界环境没有能量交换,即环境传导和热辐射忽略不计,因此,由热力学第一定律可知:
| $ U = {U_{\rm{e}}} + {U_{\rm{d}}}, $ | (1) |
其中,弹性应变能的计算公式为:
| $ {U_{\rm{e}}} = \frac{1}{2}{\sigma _1}{\varepsilon _{{\rm{el}}}} + \frac{1}{2}{\sigma _2}{\varepsilon _{{\rm{e}}2}} + \frac{1}{2}{\sigma _3}{\varepsilon _{{\rm{e}}3}}, $ | (2) |
| $ {\varepsilon _{{\rm{e}}i}} = \frac{1}{{{E_{\rm{u}}}}}\left[ {{\sigma _i} - {\nu _{\rm{u}}}\left( {{\sigma _j} + {\sigma _k}} \right)} \right], $ | (3) |
| $ {U_{\rm{e}}} = \frac{1}{{2{E_0}}}\left[ {\sigma _1^2 + \sigma _2^2 + \sigma _3^2 - 2\nu \left( {{\sigma _1}{\sigma _2} + {\sigma _2}{\sigma _3} + {\sigma _1}{\sigma _3}} \right)} \right]. $ | (4) |
式中:U为外界输入的总能量;Ue为弹性应变能,即积聚在岩体内的能量;Ud为耗散能,即用于受载岩体内部损伤和塑性变形的能量;σi(i=1, 2, 3)为主应力;εi(i=1, 2, 3)为主应变,规定压应变为正,则岩石受压侧向膨胀ε2、ε3为负值;εei(i=1, 2, 3)为相应的弹性应变;E0为初始弹模;Eu和νu分别为卸载弹模和泊松比.文献[27-28]采用E0近似代替Eu、ν代替νu.
由式(4)进一步得出岩石单轴压缩起裂弹性应变能和峰值弹性应变能:
| $ {U_{{\rm{e}}, {\rm{ci}}}} = \frac{{\sigma _{{\rm{ci}}}^2}}{{2{E_0}}}, $ | (5) |
| $ {U_{{\rm{e}}, {\rm{c}}}} = \frac{{\sigma _{\rm{c}}^2}}{{2{E_0}}}. $ | (6) |
式中:Ue, ci为起裂弹性应变能;Ue, c为峰值弹性应变能;σci为起裂应力;σc为峰值强度.
通过分析可知,岩石起裂弹性应变能与起裂应力,峰值弹性应变能与峰值强度存在内在联系,即
| $ {U_{\rm{e}}} = f\left( {{\sigma _{{\rm{ci}}}}, {\sigma _{\rm{c}}}} \right). $ | (7) |
Griffith强度理论认为脆性材料中存在许多细小裂纹或缺陷,在外力作用下,这些裂纹和缺陷附近产生应力集中现象,当力达到一定程度时,裂纹开始起裂.文献[29]认为应力强度因子达到KIC(KIC为岩石断裂韧性)时,裂纹开始起裂扩展,但未建立岩石拉伸或单轴抗压强度与裂纹起裂应力水平的关系.文献[30]在此基础上研究表明,σt=6.88 KIC,σt为岩石抗拉强度.文献[31]研究了不同粒度尺度的裂纹起裂,假设σc/σt=8~12,σc=(55~82)KIC,并基于Griffith强度准则得到σci=Kσc=8σt,K为起裂应力水平,根据岩石种类分布在0.3~0.6区间.文献[12]在文献[29-31]的基础上,分析了起裂应力与单轴抗拉和抗压强度之间的关系,对脆性指标B13、B14、B15和B16进行了重新定义:
| $ {B_{13}} = {\sigma _{\rm{c}}}/{\sigma _{\rm{t}}} = 8{\sigma _{\rm{c}}}/{\sigma _{{\rm{ci}}}}, $ | (8) |
| $ \begin{array}{*{20}{c}} {{B_{14}} = \left( {{\sigma _{\rm{c}}} - {\sigma _{\rm{t}}}} \right)/\left( {{\sigma _{\rm{c}}} + {\sigma _{\rm{t}}}} \right) = }\\ {\left( {8{\sigma _{\rm{c}}} - {\sigma _{{\rm{ci}}}}} \right)/\left( {8{\sigma _{\rm{c}}} + {\sigma _{{\rm{ci}}}}} \right), } \end{array} $ | (9) |
| $ {B_{15}} = \frac{{{\sigma _{\rm{c}}}{\sigma _{{\rm{ci}}}}}}{{16}}, $ | (10) |
| $ {B_{16}} = {\left( {\frac{{{\sigma _{\rm{c}}}{\sigma _{{\rm{ci}}}}}}{{16}}} \right)^{\frac{1}{2}}}. $ | (11) |
通过以上分析可知,脆性指标与起裂应力和峰值强度同样存在内在关系,即
| $ B = f\left( {{\sigma _{{\rm{ci}}}}, {\sigma _{\rm{c}}}} \right). $ | (12) |
综上所述,脆性指标与弹性应变能之间必然有一定相关性,本文通过理论计算和拟合分析对单轴压缩试验结果进行这种内在关系的探讨.
3 算例分析 3.1 算例1:三山岛花岗岩试验中花岗岩试样取自三山岛金矿深部,该花岗岩主要矿物成分为斜长石、钾长石、石英和黑云母,其体积分数分别为44%、20%、32%、4%.主要矿物粒度从2~4 mm不等.将岩样加工成16个尺寸为Φ50 mm×100 mm的圆柱体试样,使用北京科技大学GAW-2 000型微机控制电液伺服刚性压力试验机(图 1)进行单轴压缩试验,采用引伸计测量试样的轴向与侧向应变,试验全过程采用位移控制方式,加载速率为0.01 mm/min,直至加载到试样破坏.数据采样间隔为0.1 s.以S01-01试样为例,采用侧向应变差法确定三山岛花岗岩试样的起裂应力值,如图 2所示,剩余试样起裂应力的确定将不再赘述.试验获得的力学与能量参数值见表 2.

|
图 1 试验设备 Fig. 1 Test equipment |
|
图 2 S01-01试样起裂应力确定 Fig. 2 Identification of crack initiation stress of S01-01 specimen |
| 表 2 三山岛花岗岩试样力学与能量参数汇总 Tab. 2 Summary of mechanics and energy parameters of Sanshandao granite samples |
为研究脆性指标与弹性应变能之间的关系,本文分别采用指数函数、对数函数、幂函数和线性函数等不同函数形式进行拟合,统计每种函数拟合的相关系数,该值越大表明脆性指标与弹性应变能二者之间的相关性越强,最后选取相关系数最大的函数作为最终拟合函数.
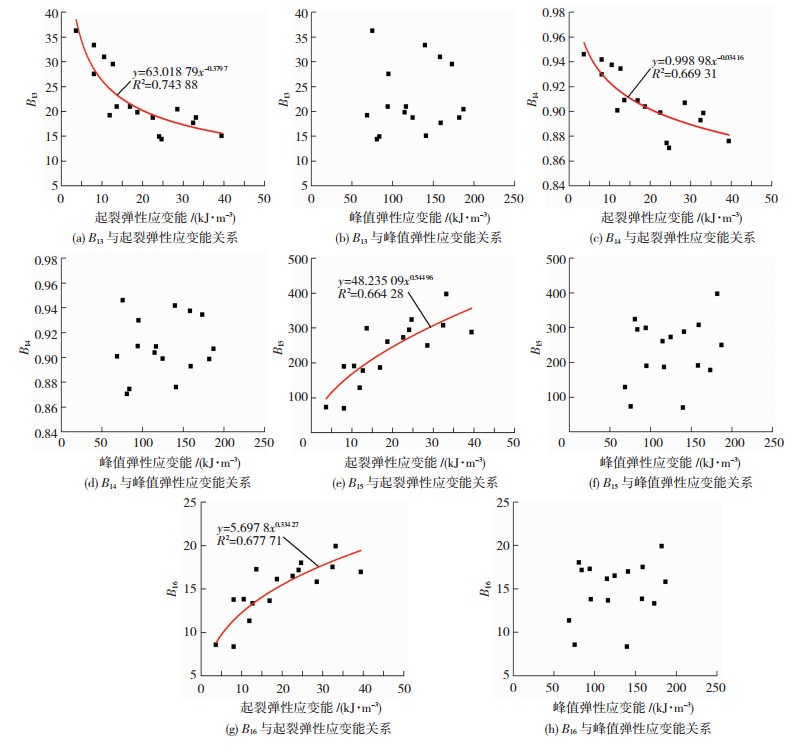
基于表 2力学与能量参数结果,探讨三山岛花岗岩不同脆性指标(B13、B14、B15和B16)与弹性应变能的内在关系.从图 3可知,脆性指标B13、B14、B15和B16与起裂弹性应变能(单变量)符合幂函数关系,函数拟合的相关性系数分别为0.743 88、0.669 31、0.664 28、0.677 71,该组试验数据拟合程度一般,试验数据具有一定程度的离散性,而脆性指标B13、B14、B15和B16与峰值弹性应变能(单变量)之间无明显函数关系.
|
图 3 三山岛花岗岩弹性应变能与不同脆性指标关系 Fig. 3 Relationship of elastic strain energy of Sanshandao granite with different brittleness indexes |
文献[32]对新疆天湖花岗闪长岩试样进行了单轴压缩试验和声发射监测,试样加载与声发射测量保持同步.天湖花岗闪长岩主要由碱性长石、斜长石、石英和黑云母组成,斑晶主要为钾长石,呈浅肉红色,粒度为5~10 mm.根据试验获得的数据,采用侧向应变差法确定天湖花岗闪长岩的起裂应力值.试验获得的力学与能量参数值见表 3.
| 表 3 天湖花岗闪长岩试样力学与能量参数汇总[32] Tab. 3 Summary of mechanics and energy parameters of Tianhu granodiorite samples[32] |
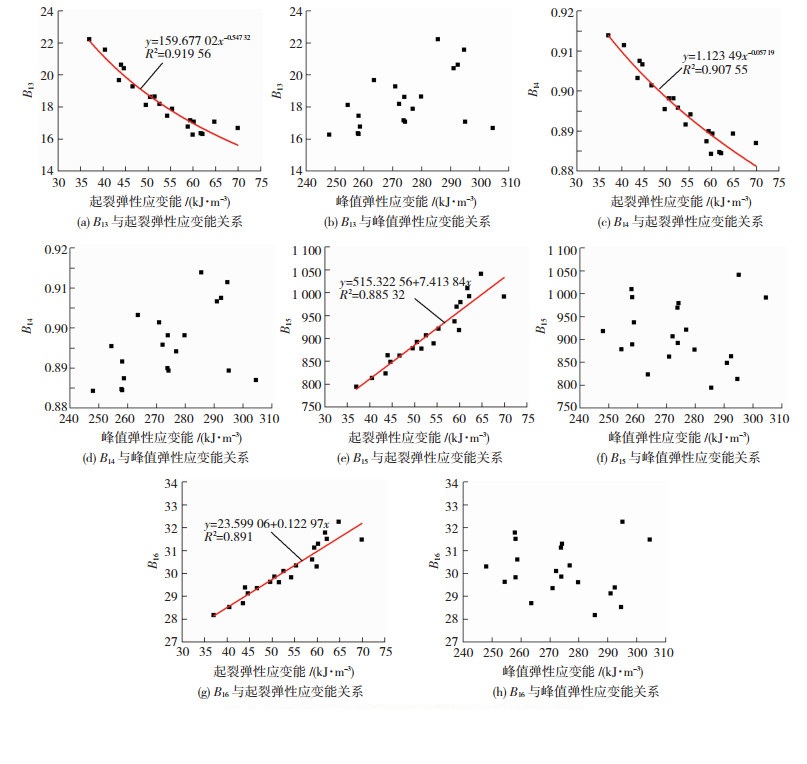
基于表 3力学与能量参数结果,探讨天湖花岗闪长岩不同脆性指标(B13、B14、B15和B16)与弹性应变能的内在关系.从图 4可知,脆性指标B13、B14与起裂弹性应变能(单变量)符合幂函数关系,函数拟合的相关性系数分别为0.919 56和0.907 55,脆性指标B15、B16与起裂弹性应变能(单变量)符合线性函数关系,拟合的相关性系数分别为0.885 32和0.891,该组试验数据拟合程度较好,数据的整体规律和变化趋势十分明显,而脆性指标B13、B14、B15和B16与峰值弹性应变能(单变量)之间无明显函数关系.通过与算例1结果对比可知,该组试验数据更好地给出了脆性指标与起裂弹性应变能之间的函数关系.
|
图 4 天湖花岗闪长岩弹性应变能与不同脆性指标关系 Fig. 4 Relationship of elastic strain energy of Tianhu granodiorite with different brittleness indexes |
本文通过幂函数和线性函数拟合发现脆性指标B13、B14、B15和B16与起裂弹性应变能(单变量)之间具有明显的相关性,且脆性指标B13、B14与起裂弹性应变能之间符合幂函数关系,脆性指标B15、B16与起裂弹性应变能之间符合幂函数或线性函数关系.这种函数关系并非偶然,而是客观存在的结果.因此,结合表 1中B13、B14、B15和B16的定义方法,联立算例1、2中的拟合公式和式(5)、(6),脆性指标B13、B14、B15和B16可被重新定义为:
| $ {B_{13}} = 8{\left( {\frac{{{U_{{\rm{e}}, {\rm{c}}}}}}{{{U_{{\rm{e}}, {\rm{ci}}}}}}} \right)^{0.5}} \approx {a_1}U_{{\rm{e}}, {\rm{ci}}}^{{b_1}}, $ | (13) |
| $ {B_{14}} = \frac{{8{{\left( {\frac{{{U_{{\rm{e, c}}}}}}{{{U_{{\rm{e, ci}}}}}}} \right)}^{0.5}} - 1}}{{8{{\left( {\frac{{{U_{{\rm{e, c}}}}}}{{{U_{{\rm{e, ci}}}}}}} \right)}^{0.5}} + 1}} \approx {a_2}U_{{\rm{e, c}}}^{{b_2}}, $ | (14) |
| $ {B_{15}} = \frac{{{E_0}{{\left( {{U_{\rm{e}}} \cdot {U_{{\rm{e}}, {\rm{ci}}}}} \right)}^{0.5}}}}{8} \approx {a_3}U_{{\rm{e}}, {\rm{ci}}}^{{b_3}} \approx {a_4} + {b_4}{U_{{\rm{e}}, {\rm{ci}}}}, $ | (15) |
| $ {B_{16}} = {\left( {\frac{{{E_0}{{\left( {{U_{\rm{e}}} \cdot {U_{{\rm{e}}, {\rm{ci}}}}} \right)}^{0.5}}}}{8}} \right)^{0.5}} \approx {a_5}U_{{\rm{e}}, {\rm{ci}}}^{{b_5}} \approx {a_6} + {b_6}{U_{{\rm{e}}, {\rm{ci}}}}. $ | (16) |
式中a1、a2、a3、a4、a5、a6、b1、b2、b3、b4、b5和b6均为拟合常数.
通常起裂和峰值弹性应变能的计算方法是从应力-应变曲线上选取起裂应力和峰值强度,然后在起裂点和峰值点处分别进行卸载,最后通过积分计算面积得到,而式(5)和(6)的应用,可以避免卸载点选取困难的问题,不再需要积分计算面积.由式(13)~(16)可知,新脆性指标可由起裂和峰值弹性应变能(双变量)获得,或由起裂弹性应变能(单变量)获得.另外,脆性指标B13与峰值弹性应变能都为岩爆倾向性评价指标,脆性指标B13也称岩石脆性系数判据,峰值弹性应变能也称线弹性能判据,综合两种指标可重新定义岩爆分类标准.因此,脆性指标与峰值弹性应变能关系式的构建,对于研究岩爆倾向性具有重要意义.
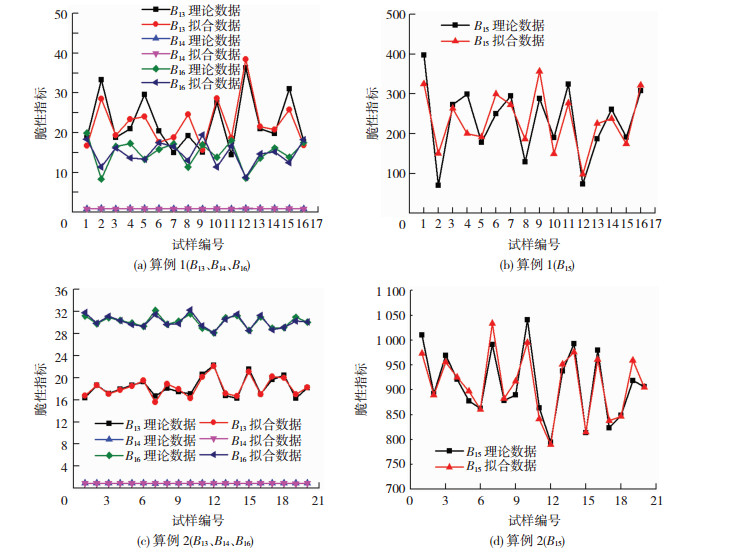
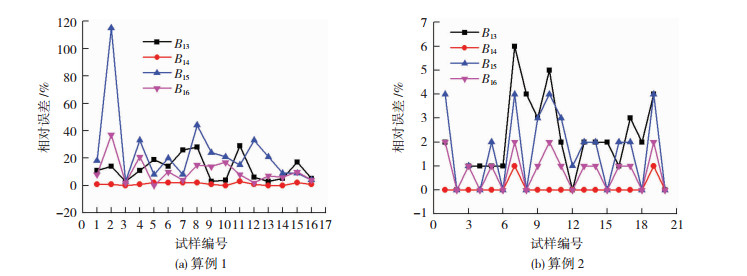
图 5为算例1和算例2的理论计算数据与拟合数据的对比,即理论计算数据采用起裂和峰值弹性应变能(双变量)得出脆性指标,拟合数据采用起裂弹性应变能(单变量)得出脆性指标.图 6为拟合计算数据的相对误差百分比,误差计算方法为:相对误差=|理论值-拟合值|/理论值.从图 6(a)可知,算例1脆性指标B13、B14、B15和B16拟合计算结果相对误差范围分别为3% ~ 29%、0% ~ 3%、3% ~ 33% (剔除两个误差较大的数据)、0%~37%,从图 6(b)可知,算例2脆性指标B13、B14、B15和B16拟合计算结果相对误差范围分别为0% ~ 6%、0% ~ 1%、0%~4%、0% ~ 2%.由图 6可知,算例1试验数据拟合结果相对误差较大,这是由于三山岛花岗岩试样试验数据具有一定程度的离散性,导致离散性的原因主要来自于三山岛花岗岩试样内部存在较多不同产状的天然裂隙,因此导致试验过程中单轴抗压强度和弹性模量值波动较大,相比之下,算例2中天湖花岗闪长岩试样内部天然裂隙较少,试验数据拟合结果较好.通过对比发现三山岛花岗岩试验数据虽具有一定程度的离散性,但脆性指标与起裂弹性应变能之间仍然呈一定趋势变化,更加说明这种内在关系的客观存在,并且试样内部均质性越好,规律性就越强,在今后还需进行大量试验以便进一步论证脆性指标与起裂弹性应变能之间关系的正确性.综上分析可见,相对其他指标而言,本文建立了岩石脆性指标与弹性应变能的数学关系,为岩体工程脆性指标的研究提供了新参考.
|
图 5 理论与拟合计算方法脆性指标结果对比 Fig. 5 Comparisons of calculation results of brittlenessindexes using theory and fitting calculation methods |
|
图 6 拟合计算相对误差 Fig. 6 Fitting calculation relative error |
1) 采用理论分析与室内单轴压缩试验得出了脆性指标与弹性应变能的内在联系,对试验数据进行拟合分析,发现脆性指标B13、B14与起裂弹性应变能(单变量)符合幂函数关系,脆性指标B15、B16与起裂弹性应变能(单变量)符合幂函数或线性函数关系,而脆性指标B13、B14、B15和B16与峰值弹性应变能(单变量)之间无明显函数关系.
2) 根据理论公式和拟合公式可知,新脆性指标可由起裂和峰值弹性应变能(双变量)获得,或由起裂弹性应变能(单变量)获得.脆性指标B13与峰值弹性应变能都为岩爆倾向性评价指标,脆性指标与峰值弹性应变能关系式的构建,对于研究岩爆倾向性具有重要意义.
3) 分析两种岩石试验算例可知,三山岛花岗岩试样拟合数据相对误差范围较大,但试验数据仍然呈一定规律变化,天湖花岗闪长岩试样拟合数据相对误差范围较小,试验数据规律性更加可靠和准确.因此,采用起裂弹性应变能的岩石脆性指标计算方法具有一定的可靠性,在今后的研究工作中还需进一步探讨.
| [1] |
夏英杰, 李连崇, 唐春安, 等. 基于峰后应力跌落速率及能量比的岩体脆性特征评价方法[J]. 岩石力学与工程学报, 2016, 35(6): 1141. XIA Yingjie, LI Lianchong, TANG Chun′an, et al. Rock brittleness evaluation based on stress dropping rate after peak stress and energy ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(6): 1141. DOI:10.13722/j.cnki.jrme.2015.0803 |
| [2] |
TARASOV B, POTVIN Y. Universal criteria for rock brittleness estimation under triaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59: 57. DOI:10.1016/j.ijrmms.2012.12.011 |
| [3] |
李庆辉, 陈勉, 金衍, 等. 页岩脆性的室内评价方法及改进[J]. 岩石力学与工程学报, 2012, 31(8): 1681. LI Qinghui, CHEN Mian, JIN Yan, et al. Indoor evaluation method for shale brittleness and improvement[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1681. DOI:10.3969/j.issn.1000-6915.2012.08.023 |
| [4] |
周辉, 孟凡震, 张传庆, 等. 基于应力-应变曲线的岩石脆性特征定量评价方法[J]. 岩石力学与工程学报, 2014, 33(6): 1114. ZHOU Hui, MENG Fanzhen, ZHANG Chuanqing, et al. Quantitative evaluation of rock brittleness based on stress-strain curve[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1114. DOI:10.13722/j.cnki.jrme.2014.06.004 |
| [5] |
陈国庆, 赵聪, 魏涛, 等. 基于全应力-应变曲线及起裂应力的岩石脆性特征评价方法[J]. 岩石力学与工程学报, 2018, 37(1): 51. CHEN Guoqing, ZHAO Cong, WEI Tao, et al. Evaluation method of brittle characteristics of rock based on full stress-strain curve and crack initiation stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 51. DOI:10.13722/j.cnki.jrme.2017.0499 |
| [6] |
BISHOP A W. Progressive failure with special reference to the mechanism causing it[C]//Proceedings of the Geotechnical Conference. Oslo: [s.n.], 1967: 142
|
| [7] |
HAJIABDOLMAJID V, KAISER P. Brittleness of rock and stability assessment in hard rock tunneling[J]. Tunnelling and Underground Space Technology, 2003, 18(1): 35. DOI:10.1016/S0886-7798(02)00100-1 |
| [8] |
HUCKA V, DAS B. Brittleness determination of rocks by different methods[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1974, 11(10): 389. DOI:10.1016/0148-9062(74)91109-7 |
| [9] |
AUBERTIN M, GILL D E, SIMON R. On the use of the brittleness index modified (BIM) to estimate the post peak behavior or rocks[C]//1st North American Rock Mechanics Symposium. Austin: American Rock Mechanics Association, 1994: 945
|
| [10] |
GEORGE E A. Brittle failure of rock material-test results and constitutive models[M]. Rotterdam: [s.n.], 1995: 123
|
| [11] |
ALTINDAG R. Assessment of some brittleness indexes in rock-drilling efficiency[J]. Rock Mechanics and Rock Engineering, 2010, 43(3): 361. DOI:10.1007/s00603-009-0057-x |
| [12] |
王宇, 李晓, 武艳芳, 等. 脆性岩石起裂应力水平与脆性指标关系探讨[J]. 岩石力学与工程学报, 2014, 33(2): 264. WANG Yu, LI Xiao, WU Yanfang, et al. Research on relationship between crack initiation stress level and brittleness indices for brittle rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 264. DOI:10.13722/j.cnki.jrme.2014.02.003 |
| [13] |
RICKMAN R, MULLEN M, PETRE E, et al. A practical use of shale petrophysics for stimulation design optimization: all shale plays are not clones of the Barnett shale[C]//SPE annual technical conference and exhibition. Denver, USA: Society of Petroleum Engineers, 2008.DOI: 10.2118/115258-MS
|
| [14] |
LAWN B R, MARSHALL D B. Hardness, toughness and brittleness: an indentation analysis[J]. Journal of American Ceramic Society, 1979, 62(7/8): 347. DOI:10.1111/j.1151-2916.1979.tb19075.x |
| [15] |
QUINN J B, QUINN G D. Indentation brittleness of ceramics: a fresh approach[J]. Journal of Materials Science, 1997, 32(16): 4331. DOI:10.1023/A:1018671823059 |
| [16] |
BLINDHEIM O T, BRULAND A. Boreability testing[C]//Norwegian TBM tunneling. Trondheim, Norway: Norwegian Soil and Rock Engineering Association, 1998: 29
|
| [17] |
PROTODYAKONOV M M. Mechanical properties and drillability of rocks[C]//Proceedings of the 5th Symposium on Rock Mechanics. Twin Cities, USA: University of Minnesota Press, 1963: 103
|
| [18] |
YAGIZ S. An investigation on the relationship between rock strength and brittleness[C]//Proceedings of the 59th Geological Congress of Turkey. Ankara, Turkey: MTA General Directory Press, 2006: 352
|
| [19] |
COPUR H, BILGIN N, TUNCDEMIR H, et al. A set of indices based on indentation test for assessment of rock cutting performance and rock properties[J]. Journal of the South African Institute of Mining and Metallurgy, 2003, 103(9): 589. |
| [20] |
BAZANT Z P, KAZEMI M T. Determination of fracture energy, process zone length and brittleness number from size effect, with application to rock and concrete[J]. International Journal of Fracture, 1990, 44: 111. DOI:10.1007/BF00047063 |
| [21] |
BRACE W F, PAULDING B W, SCHOLZ C H. Dilatancy in the fracture of crystalline rocks[J]. Journal of Geophysical Research, 1966, 71(16): 3939. DOI:10.1029/JZ071i016p03939 |
| [22] |
LAJTAI E Z. Brittle fracture in compression[J]. International Journal of Fracture Mechanics, 1974, 10(4): 525. DOI:10.1007/BF00155255 |
| [23] |
MARTIN C D, CHANDLER N A. The progressive fracture of Lac du Bonnet granite[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1994, 31(6): 643. DOI:10.1016/0148-9062(94)90005-1 |
| [24] |
NICKSIAR M, MARTIN C D. Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks[J]. Rock Mechanics and Rock Engineering, 2012, 45(4): 607. DOI:10.1007/s00603-012-0221-6 |
| [25] |
ZHAO X G, WANG J, MA L K, et al. Acoustic emission behaviors of the Beishan granite under uniaxial and triaxial compression conditions[C]//Proceedings of the 3rd ISRM Sinorock Symposium. London: CRC Press, 2013
|
| [26] |
黄丹, 李小青. 基于微裂纹发育特性的大理岩特征强度数值模拟研究[J]. 岩土力学, 2017, 38(1): 253. HUANG Dan, LI Xiaoqing. Numerical simulation research on characteristic strength of marble based on development of microcrack[J]. Rock and Soil Mechanics, 2017, 38(1): 253. DOI:10.16285/j.rsm.2017.01.032 |
| [27] |
尤明庆, 苏承东. 大理岩试样循环加载强化作用的试验研究[J]. 固体力学学报, 2009, 29(1): 66. YOU Mingqing, SU Chengdong. Experimental study on strengthening of marble specimen in cyclic loading of uniaxial or pseudo-triaxial compression[J]. Chinese Journal of Solid Mechanics, 2009, 29(1): 66. DOI:10.19636/j.cnki.cjsm42-1250/o3.2008.01.010 |
| [28] |
余贤斌, 谢强, 李心一, 等. 岩石直接拉伸与压缩变形的循环加载实验与双模量本构模型[J]. 岩土工程学报, 2005, 27(9): 988. YU Xianbin, XIE Qiang, LI Xinyi, et al. Cycle loading tests of rock samples under direct tension and compression and bi-modular constitutive model[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(9): 988. DOI:10.3321/j.issn:1000-4548.2005.09.003 |
| [29] |
ERDOGAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Fluids Engineering, 1963, 85(4): 519. DOI:10.1115/1.3656897 |
| [30] |
ZHANG Z X. An empirical relation between mode I fracture toughness and the tensile strength of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(3): 401. DOI:10.1016/S1365-1609(02)00032-1 |
| [31] |
CAI M. Practical estimates of tensile strength and Hoek-Brown strength mi of brittle rocks[J]. Rock Mechanics and Rock Engineering, 2010, 43: 167. DOI:10.1007/s00603-009-0053-1 |
| [32] |
李鹏飞, 赵星光, 蔡美峰. 压缩条件下岩石启裂应力的识别方法探讨--以新疆天湖花岗闪长岩为例[J]. 岩土力学, 2015, 36(8): 2323. LI Pengfei, ZHAO Xingguang, CAI Meifeng. Discussion on approaches to identifying cracking initiation stress of rocks under compression condition:a case study of Tianhu granodiorite in Xinjiang autonomous region[J]. Rock and Soil Mechanics, 2015, 36(8): 2323. DOI:10.16285/j.rsm.2015.08.027 |
 2019, Vol. 51
2019, Vol. 51


