纳米材料广泛用于微机电系统与纳机电系统的加工制造[1].然而在纳米材料的加工制造过程中,纳米材料难以根据加工要求实现去除过程,这是由于缺少纳米材料加工机理研究,尤其是对纳米加工过程中材料内部位错的演生过程及材料内应力的传递方式等方面的研究.因此,研究多晶材料如纳米多晶铜在纳米加工过程中的变形机理对提升纳米材料加工的相关技术具有重要意义[2].
通常情况下,可采用多种实验方法研究多晶铜的纳米加工变形机理,包括纳米压痕[3]、原子力显微镜法[4]、扫描电镜法[5]、透射电镜法[6]、聚焦粒子束法[7]及X射线衍射法[8]等.这些实验方法均受到实验条件及测试尺度的限制,而计算模拟方法能够直接分析材料纳米加工中的塑性变形及应力变化,更适用于材料变形机理的研究.计算模拟方法中第一原理计算方法[9]受限于计算速度缓慢且耗时长;有限元模拟[10]受限于难以建立纳米尺度的模型;准连续方法[11]受限于难以分析位错结构的演生过程;分子动力学方法[12-13](molecular dynamics,MD)被广泛用于材料的纳米加工机理研究中.尽管大量学者针对多晶铜纳米加工机理进行了研究,包括纳米压痕力[14],应变速率[15],内应力[16-17],弹性模量[18]及摩擦行为[19]等,然而, 关于晶粒度对多晶铜纳米压痕过程位错的演生及塑性变形机理仍有待进一步研究.此外,大量研究结果表明晶界结构在多晶铜的纳米加工过程中具有重要影响[20-23].
本工作基于Poisson-Voronoi和Inverse Monte Carlo法建立大规模多晶铜纳米压痕分子动力学模型.建立了4类不同晶体结构模型,包括1个单晶铜模型与3个具有不同晶粒度多晶铜模型,通过MD模拟研究了晶粒度对位错演生及塑性变形机理的影响.研究了压痕力、位错形核与扩展、内应力、原子势能分布的影响.对多晶铜的晶粒度及晶界结构进行了分析,以期为多晶材料的纳米加工机理的研究提供一些理论依据.
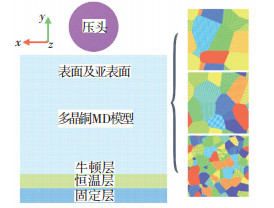
1 建模与模拟 1.1 模型的建立图 1为晶体铜纳米压痕MD模拟模型,包括单晶/多晶铜与金刚石刚体压头.晶体铜模型尺寸为41.5 nm×41.5 nm×41.5 nm,包含约6.16×106个铜原子.压痕实验中压头主要包括球形、圆锥形、Vicker(正方棱锥形)、Berkovich(四面体形)等[24],为获得更准确的MD模拟结果,采用直径为14.0 nm的球形金刚石压头(晶格常数为0.357 nm),压头原子数为2.5×105.由于金刚石硬度远高于铜[25],MD模型中压头被认为是刚体.多晶铜模型采用Poisson-Voronoi和Inverse Monte Carlo法建立,包括晶粒内部与晶界两种结构,如图 1所示,具体过程请参考本课题组前期工作[26-27].建立模型的简要过程为:1)建立Voronoi胞拓扑结构模型并保证Voronoi胞具有与实际晶粒相近的尺寸,使Voronoi胞尺寸满足Monte Carlo分布;2)建立单晶材料的晶体结构模型用于填充Voronoi胞;3)通过识别Voronoi胞拓扑模型中晶粒及晶界结构与2)中原子结构模型原子位置的对应关系,填充Voronoi胞并获得多晶体模型.本工作研究的多晶铜模型分别具有20、50与500个晶粒,对应分别具有19、14与6.5 nm的晶粒度.本工作中4个模型分别为:模型1,单晶铜模型;模型2,多晶铜模型,晶粒度19 nm;模型3,多晶铜模型,晶粒度14 nm;模型4,多晶铜模型,晶粒度6.5 nm. MD模型的X轴与Z轴方向采用周期性边界条件以消除仿真中尺寸效应的影响. MD模型沿Y轴被分别划分为牛顿层、恒温层与固定层.
|
图 1 晶体铜纳米压痕分子动力学模拟模型 Fig. 1 3D model of single-crystalline and polycrystalline copper with different grain sizes |
压头初始位置位于多晶铜表面晶粒上方1 nm处,远大于压头原子与工件原子自由程.采用共轭梯度法进行能量最小化并在等温等压系综(NPT系综)采用Nose-Hoover热浴法在293 K下进行弛豫,弛豫时间为100 ps.弛豫后的模型在等体积能力系综(NVE系综)进行压痕MD模拟.模拟时间步长为1 fs,远小于碳原子与铜原子间的振荡频率.压头设定为理想化刚性模型,即在压痕模拟过程中,压头模型结构不会在力的作用下发生改变,采用恒定速率10 m/s压痕,压痕深度为8 nm,期间每隔0.5 nm记录一次数据,以测量系统在该压痕深度下各原子的坐标及应力、原子势能等模拟参数.
压头压入多晶铜是对其稳定的fcc晶体结构的破坏过程,位错形核并滑移,破坏多晶铜原有的稳定状态.采用共近邻分析法分析多晶铜在纳米压痕过程中位错的形核及扩散规律.本工作主要针对材料内应力包括静水压力(hydrostatic stress,HY)与范式等效应力(von Mises stress,VM)、原子势能(potential energy,PE)分析多晶铜在压痕过程中的内应力和能量分布,其中静水压力与范式等效应力的计算方法请参考本课题组前期工作[28-30].
2 结果与讨论 2.1 纳米压痕力图 2为单晶铜与不同晶粒度多晶铜纳米压痕分子动力学模拟的压痕力-压痕深度曲线.

|
模型1—单晶铜;模型2—19 nm多晶铜;模型3—14 nm多晶铜;模型4—6.5 nm多晶铜 图 2 单晶及多晶铜纳米压痕力曲线 Fig. 2 Indentation force of single-crystalline and polycrystalline copper |
纳米压痕中存在3个方向的纳米压痕力,由于正交于压头运动方向(X轴、Z轴)的2个纳米压痕力在压痕过程中变化不明显,其压痕力在F=0压力线附近波动,因而与压头运动方向(Y轴)一致的压痕力为本工作的研究对象.模拟结果表明,多晶铜纳米压痕的压痕力为nN级,纳米压痕力随压痕深度增大呈近似线性增长.由于本工作中的多晶铜模型与文献模型的晶粒度具有一定的差异[31-32],此时压痕力曲线将受到Hall-Petch效应的影响,导致纳米压痕曲线增长率产生差异性.在纳米压痕过程中伴随位错的形核与扩展过程,同时伴随有多晶铜原子势能的累积与释放,多种因素导致了纳米压痕力曲线具有一定波动.分析发现,随着压痕深度的增加,单晶铜的纳米压痕力始终为最大,其次是平均晶粒尺寸为19 nm的多晶铜和平均晶粒尺寸14 nm的多晶铜,而平均晶粒尺寸为6.5 nm的多晶铜的纳米压痕力最低.这表明随着平均晶粒尺寸的减小,多晶铜在纳米压痕过程中出现软化现象[33-34].此外,当压痕深度为0~4 nm时,由于较大数量的晶界更易引起晶界的滑移运动,这导致了平均晶粒尺寸较小的多晶铜的纳米压痕力曲线产生了更剧烈的波动.当压痕深度为4~7 nm时,多晶铜的纳米压痕力曲线的波动逐渐降低,这主要是由于多晶铜在较大压痕深度时产生了显著的塑性变形,大量堆积于晶粒内部及晶界的位错抑制了晶界的滑移运动[35].
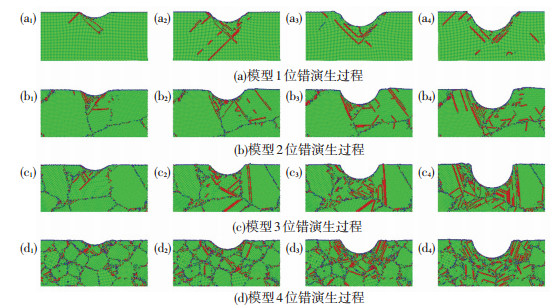
2.2 晶体铜位错演变过程分析为了更好地分析单晶和多晶铜中纳米压痕引起的塑性变形,纳米压痕过程中不同纳米压痕深度时晶体铜内部的缺陷演变如图 3所示.在图 3(a1)中,当压痕深度为2.0 nm时,对应的接触区域为4.9 nm,最大静水压力为3.37 GPa,最大范式等效应力为8.14 GPa.当压痕深度增加到6.5 nm时,最大静水压力为12.30 GPa,最大范式等效应力为14.87 GPa.由于较高的静水压力和范式等效应力[36],位错的形核与扩展主要存在于压头下方的区域.随着纳米压痕深度的增加,单晶铜中的位错在压头周围成核并扩展,随后沿{111}滑移面上缓慢滑动[37].可以看出,缺陷演化过程对纳米压痕过程的塑性变形机制起着重要的作用.
|
图 3 单晶及多晶铜纳米压痕位位错演生过程 Fig. 3 Defect evolution of single-crystalline and polycrystalline copper |
当纳米压痕深度为2.0 nm时,晶界结构能够有效地限制位错的扩展并吸收一定数量的位错,从而约束位错的分布范围.然而,随着压痕深度的增大,当晶界位置不断累积内应力与原子势能,产生应力及势能集中时,位错也会在晶界区域形核并扩散,最终穿越晶界面并向相邻晶粒内部继续滑移[38].在模型2与模型3中,缺陷扩展主要存在于压头下方较大的晶粒中,并沿{111}滑移面向晶粒周围的晶界结构滑移.当纳米压痕深度为5.0 nm时,晶界难以限制位错的扩展运动,导致位错穿过晶界并在相邻晶粒中的{111}滑移面滑动.在模型4中,低晶粒度的多晶铜具有较大数量的晶界结构,因而多晶铜具有较大的弹性应变能量,位错将被约束于压头周围的若干个晶粒中,最终导致低晶粒度的多晶铜位错分布范围最小.在单晶铜纳米压痕中,缺陷沿不同的{111}滑移面进行滑移运动,位错在压头下端相交形成“V形”缺陷区域,这与以往MD模拟结果一致[39].缺陷演变过程与内应力、原子势能相关,高内应力与高势能可为裂纹的形成提供有利条件.
如图 4(a)所示,当纳米压痕深度<4.0 nm时,随着多晶铜平均晶粒度的增加,缺陷分布范围的宽度先增大后减小.同时,缺陷分布范围的深度随着多晶铜平均晶粒度的增大而增大.另外,发现沿水平方向的缺陷演变分布比垂直方向(压头运动方向)的缺陷演变分布更快且范围更大.这主要是由于以下两方面原因.其一是由于晶界界面结构疏松且不规则,导致了晶界的内应力和原子势能高于晶粒内部,这将限制多晶铜的纳米压痕运动过程;其二是由于压头引起的沿压痕方向的高静水压力和范式等效应力能够限制位错的扩展,导致位错更易沿着水平方向扩展.在模型2和模型3中,由于缺陷均首先在较大的晶粒中形核与扩展,随后位错穿过晶界结构并向相邻晶粒扩展,这导致模型2和模型3的位错的分布范围变化相似.在模型4中,较小的平均晶粒度使多晶铜具有更多的晶界抑制缺陷扩展并吸收位错[40],因而可获得更好的材料表面及亚表面结构. 图 4(b)为缺陷原子数随纳米压痕深度的变化曲线.发现多晶铜的晶界结构及平均晶粒度大小在缺陷演化过程中起重要作用,较小的平均晶粒尺寸可以减少多晶铜中缺陷原子的数量.

|
图 4 晶体铜纳米压痕过程位错沿各方向分布范围 Fig. 4 Defect distribution of single-crystalline and polycrystalline copper during nanoindentation process along different directions |
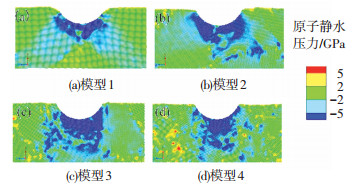
为了进一步分析多晶铜纳米压痕过程中塑性变形导致的内应力传递过程,对4个模型表面及亚表面局部区域进行提取并计算各铜原子的内应力,得到4个模型在压痕深度为4.0 nm时的静水压力分布,如图 5所示.其中,呈压应力的铜原子采用蓝色标记,呈拉应力的铜原子采用红色标记.发现,4个模型中最大的静水压力分布区域均位于压头底端并呈压应力.由于晶界疏松且无序的结构影响[41],静水压力在多晶铜中的分布比在单晶铜中的分布更为复杂.在单晶铜模型中,位于压头底端沿压头运动方向(Y轴)具有显著的压应力梯度,如图 5(a)所示,这与实验结果一致[42].然而,在多晶铜模型中,随着多晶铜晶粒度降低,位于压头底端的压应力梯度逐渐趋于向多个方向扩展,如图 5(c)~(d)所示.这主要是由于疏松的晶界结构能够有效地吸收纳米压痕过程中压头底端产生的压应力,从而使具有较小晶粒度的多晶铜模型(模型4)的表面及亚表面中静水压力分布比具有较大晶粒度的多晶铜(模型2)更加均匀且稳定[40].
|
图 5 晶体铜纳米压痕深度4.0 nm时静水压力分布 Fig. 5 Distribution of hydrostatic pressure at indentation depth of 4.0 nm in single-crystalline and polycrystalline copper |
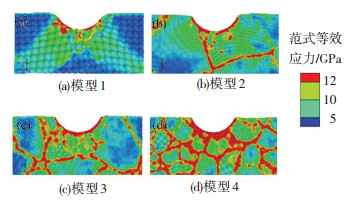
图 6为纳米压痕深度为4.0 nm时,4个晶体铜模型表面及亚表面局部区域中范式等效应力分布.其中,具有较高范式等效应力的铜原子采用红色标记,具有较低范式等效应力的铜原子采用蓝色标记.发现,在单晶铜模型的压表面中具有较高范式等效应力的铜原子分布呈“V形”,如图 6(a)所示.这主要是由于纳米压痕过程中产生的位错能够沿{111}滑移面有效地传递内应力,最终多个沿{111}滑移面传递的应力区域相交,在压头底部区域形成“V形”应力分布区域,这与前期的研究结果一致[43].在多晶铜模型中,晶界结构区域具有显著的非均匀分布的范式等效应力.位于晶界区域,尤其是位于三叉晶界及顶点团结构附近的高范式等效应力,导致了晶界与晶粒间较大的范式等效应力梯度.根据图 6(b)~(d),较小的晶粒度能够导致沿纳米压痕方向较低的应力梯度.这是由于位于晶界区域较高的范式等效应力梯度能够抑制多晶铜内部的应力传递,从而将纳米压痕过程引起的内应力限制于多晶铜亚表面区域若干个晶粒内部. 图 6的结果进一步证明了多晶铜的晶粒度对纳米压痕引起的内应力分布及内应力梯度方向具有重要影响.
|
图 6 晶体铜纳米压痕深度4.0 nm时范式等效应力分布 Fig. 6 Distribution of Von Mises stress at indentation depth of 4.0 nm in single-crystalline and polycrystalline copper |
图 7为单晶铜与多晶铜在纳米压痕深度4.0 nm时,材料表面及亚表面原子势能分布,其中具有较高原子势能的铜原子采用红色标记,具有较低原子势能的铜原子采用蓝色标记.发现与图 6及图 7中晶体铜亚表面层内应力分布范围相比,晶体铜具有较小的原子势能的分布范围.在单晶铜中具有较高原子势能的铜原子分布在压头底端形成“V形”分布区域,这与图 3(a3)中位错形成的区域形状相似.这表明缺陷在晶体铜内部的传递过程中,不仅沿{111}滑移面传递较高的内应力,同时也沿滑移面传递较高的原子势能.在多晶铜中原子分布松散且无序的晶界结构比原子排列有序的晶粒内部具有更高的原子势能,导致晶界与晶粒之间较大的原子势能梯度.随着多晶铜晶粒度的降低,由纳米压痕引起的沿压头运动方向传递的势能梯度受到位于晶界位置的高势能梯度的阻碍,最终使具有较高原子势能的铜原子分布于多晶铜亚表层若干个晶粒中.因而,在纳米压痕过程中具有较低晶粒度的多晶铜更易获得较小的高原子势能分布范围.

|
图 7 晶体铜纳米压痕深度4.0 nm时原子势能分布 Fig. 7 Distribution of atomic potential energy at indentation depth of 4.0 nm in single-crystalline and polycrystalline copper |
采用MD模拟计算并统计晶体铜模型中各铜原子的静水压力、范式等效应力及原子势能,内应力及原子势能随压痕深度的变化如图 8所示.
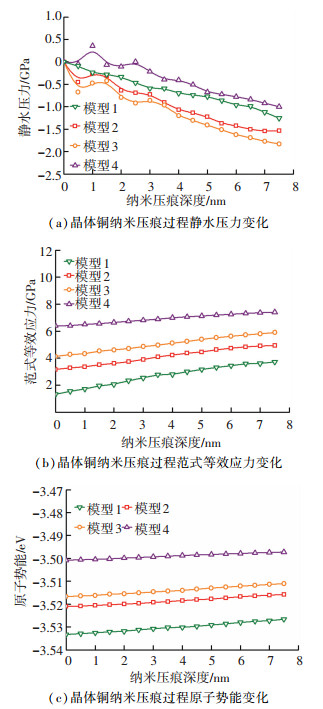
|
图 8 晶体铜纳米压痕过程内应力及原子势能变化曲线 Fig. 8 Variation of hydrostatic pressure, Von Mises stress, and atomic potential energy with indentation depth in single-crystalline and polycrystalline copper |
纳米压痕过程中,单晶铜与多晶铜内部静水压力均为压应力(负号),并随压痕深度的增大而增大.由于晶界结构的影响,多晶铜的静水压力曲线在压痕深度为0~4 nm区域具有一定的周期性波动.随着多晶铜晶粒度减小,静水压力曲线的增长速率先增大后减小.具有较小晶粒度的多晶铜(模型4)的静水压力最小,其次为模型1、模型2与模型3.多晶铜的范式等效应力远大于单晶铜,这是由于晶界区域具有较高的范式等效应力梯度.具有较小晶粒度的多晶铜(模型4)的范式等效应力曲线增长速率最高,其次为模型3,模型2与模型1.模拟结果表明,晶界结构能够保证纳米压痕过程中多晶铜表面及亚表面区域内应力分布的均匀与稳定.晶体铜纳米压痕过程中原子势能曲线的规律与范式等效应力曲线的规律相似,本文不再重复描述.
由纳米压痕引起的多晶铜塑性变形及位错演变过程与多晶铜的晶界结构密切相关,而晶界结构数量与多晶铜晶粒度大小密切相关.众所周知,随着多晶铜晶粒度降低,多晶铜将首先遵循Hall-Petch关系从而导致多晶铜材料硬化,随后当晶粒度降低至14.5 nm左右时,多晶铜将遵循反Hall-Petch关系从而导致多晶铜材料软化.由于本工作中涉及的MD模拟材料为具有较低晶粒度的纳米晶体铜,其遵循反Hall-Petch关系,在纳米压痕过程中多晶铜能够将高内应力及原子势能主要限制于材料的表层及亚表层区域,与此同时多晶铜的延展性也有所增大.为了进一步提高多晶材料的机械加工性能,采用具有表层及亚表层为较低晶粒度而材料内部为较大晶粒度的梯度晶粒度(grain size gradient, GSG)多晶材料,能够将多晶材料机械加工引起的内应力及原子势能限制于材料表层及亚表层,同时能够保证材料具有较高的硬度,后续的工作中将进一步研究梯度晶粒度材料的微纳加工特性及变形机理.
3 结论本文针对晶粒度进行了多晶铜表面纳米压痕模拟计算,通过分析多晶铜亚表层缺陷的演化过程、压痕力曲线、原子势能曲线等,揭示了晶粒度对多晶铜纳米压痕变形过程中的影响,得到以下结论:
1) 单晶铜与多晶铜纳米压痕过程中,由于多晶铜具有疏松的晶界结构,单晶铜纳米压痕力曲线增长率高于多晶铜纳米压痕力.由于纳米多晶铜具有反Hall-Petch关系,这将导致多晶铜材料的软化现象,最终多晶铜的纳米压痕力曲线斜率随着多晶铜晶粒度降低持续降低.
2) 位错的形核与扩展过程在单晶铜与多晶铜纳米压痕过程中,均主要存在于压头底部区域,这是由于纳米压痕过程导致了该区域具有较高的原子内应力.位错沿水平方向的扩展速度及范围远高于沿竖直方向.具有较小晶粒度的多晶铜由于具有更多的晶界结构,能够有效地将位错限制于压头附近的若干个晶粒中.
3) 在单晶铜纳米压痕过程中,存在沿压头运动方向显著的内应力梯度与原子势能梯度.在多晶铜纳米压痕过程中,随着晶粒度的降低,由于受疏松且散乱分布的晶界结构影响,内应力梯度与原子势能梯度更易沿多个方向分布,不具有确定的梯度方向.
| [1] |
RONCAGLIA A, FERRI M. Thermoelectric materials in mems and nems: A review[J]. Science of Advanced Materials, 2011, 3(3): 401. DOI:10.1166/sam.2011.1168 |
| [2] |
LIN Y H, CHEN T C. A molecular dynamics study of phase transformations in mono-crystalline Si under nanoindentation[J]. Applied Physics A, 2008, 92(3): 571. DOI:10.1007/s00339-008-4633-9 |
| [3] |
LUCCA D A, HERRMANN K, KLOPFSTEIN M J. Nanoindentation: Measuring methods and applications[J]. CIRP Annals, 2010, 59(2): 803. DOI:10.1016/j.cirp.2010.05.009 |
| [4] |
MICIC M, KLYMYSHYN N, SUH Y D, et al. Finite element method simulation of the field distribution for AFM tip-enhanced surface-enhanced Raman scanning microscopy[J]. The Journal of Physical Chemistry B, 2003, 107(7): 1574. DOI:10.1021/jp022060s |
| [5] |
FANG F, LIU B, XU Z. Nanometric cutting in a scanning electron microscope[J]. Precision Engineering, 2015, 41: 145. DOI:10.1016/j.precisioneng.2015.01.009 |
| [6] |
YAN J, ASAMI T, HARADA H, et al. Fundamental investigation of subsurface damage in single crystalline silicon caused by diamond machining[J]. Precision Engineering, 2009, 33(4): 378. DOI:10.1016/j.precisioneng.2008.10.008 |
| [7] |
VOLKERT C A. Focused ion beam microscopy and micromaching[J]. MRS Bulletin, 2007, 32(5): 389. DOI:10.1557/mrs2007.62 |
| [8] |
PELLICER E, VAREA A, PANE S, et al. Nanocrystalline electroplated Cu-Ni: Metallic thin films with enhanced mechanical properties and tunable magnetic behavior[J]. Advanced Functional Materials, 2010, 20(6): 983. DOI:10.1002/adfm.200901732 |
| [9] |
LINDAN P J D. First-principles simulation: Ideas, illustrations and the CASTEP code[J]. Journal of Physics: Condensed Matter, 2002, 14(11): 2717. DOI:10.1088/0953-8984/14/11/301 |
| [10] |
ROTERS F, EISENLOHR P, HANTCHERLI L, et al. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications[J]. Acta Materialia, 2010, 58(4): 1152. DOI:10.1016/j.actamat.2009.10.058 |
| [11] |
GUNZBURGER M, ZHANG Y. A quadrature-rule type approximation to the quasi-continuum method[J]. Multiscale Modeling & Simulation, 2009, 8(2): 571. DOI:10.1137/080722151 |
| [12] |
CASALS O, OCENASEK J, ALCALA J. Crystal plasticity finite element simulations of pyramidal indentation in copper single crystals[J]. Acta materialia, 2007, 55(1): 55. DOI:10.1016/j.actamat.2006.07.018 |
| [13] |
ZHANG K, WEERTMAN J R, EASTMAN J A. The influence of time, temperature, and grain size on indentation creep in high-purity nanocrystalline and ultrafine grain copper[J]. Applied Physics Letters, 2004, 85(22): 5197. DOI:10.1063/1.1828213 |
| [14] |
SANSOZ F, STEVENSON K D. Relationship between hardness and dislocation processes in a nanocrystalline metal at the atomic scale[J]. Physical Review B, 2011, 83(22): 224101-1. DOI:10.1103/PhysRevB.83.224101 |
| [15] |
WANG F, HUANG P, XU K. Strain rate sensitivity of nanoindentation creep in polycrystalline Al film on silicon substrate[J]. Surface and Coatings Technology, 2007, 201: 5216. DOI:10.1016/j.surfcoat.2006.07.114 |
| [16] |
ZHANG F, LIU Z, ZHOU J Q. Molecular dynamics simulation of micromechanical deformations in polycrystalline copper with bimodal structures[J]. Materials Letters, 2016, 183: 261. DOI:10.1016/j.matlet.2016.07.122 |
| [17] |
HUANG C C, CHIANG T C, FANG T H. Grain size effect on indentation of nanocrystalline copper[J]. Applied Surface Science, 2015, 353: 494. DOI:10.1016/j.apsusc.2015.06.135 |
| [18] |
LI J, GUO J W, LUO H, et al. Study of nanoindentation mechanical response of nanocrystalline structures using molecular dynamics simulations[J]. Applied Surface Science, 2016, 364: 190. DOI:10.1016/j.apsusc.2015.12.145 |
| [19] |
GAO Y, RUESTES C J, TRAMONTINA D R, et al. Comparative simulation study of the structure of the plastic zone produced by nanoindentation[J]. Journal of the Mechanics and Physics of Solids, 2015, 75: 58. DOI:10.1016/j.jmps.2014.11.005 |
| [20] |
GOEL S, FAISAL N H, LUO X, et al. Nanoindentation of polysilicon and single crystal silicon: Molecular dynamics simulation and experimental validation[J]. Journal of Applied Physics, 2014, 47: 275304-1. |
| [21] |
YAGHOOBI M, VOYIADJIS G Z. Effect of boundary conditions on the md simulation of nanoindentation[J]. Computational Materials Science, 2014, 95: 626. DOI:10.1016/j.commatsci.2014.08.013 |
| [22] |
YAGHOOBI M, VOYIADJIS G Z. Atomistic simulation of size effects in singlecrystalline metals of confined volumes during nanoindentation[J]. Computational Materials Science, 2016, 111: 64. DOI:10.1016/j.commatsci.2015.09.004 |
| [23] |
SICHANI M M, SPEAROT D E. A molecular dynamics study of the role of grain size and orientation on compression of nanocrystalline Cu during shock[J]. Computational Materials Science, 2015, 108: 226. DOI:10.1016/j.commatsci.2015.07.021 |
| [24] |
VOYIADJIS G Z, PETERS R. Size effects in nanoindentation: An experimental and analytical study[J]. Acta Mechanica, 2010, 211: 131. DOI:10.1007/s00707-009-0222-z |
| [25] |
ZHANG L, ZHAO H, DAI L, et al. Molecular dynamics simulation of deformation accumulation in repeated nanometric cutting on single-crystal copper[J]. RSC Advances, 2015, 5(17): 12678. DOI:10.1039/C4RA12317D |
| [26] |
GUO Y B, XU T, LI M. Generalized type Ⅲ internal stress from interfaces, triple junctions and other microstructural components in nanocrystalline materials[J]. Acta Materialia, 2013, 61: 4976. DOI:10.1016/j.actamat.2013.04.048 |
| [27] |
GUO Y B, XU T, LI M. Hierarchical dislocation nucleation controlled by internal stress in nanocrystalline copper[J]. Applied Physics Letters, 2013, 102(24): 241910-2. DOI:10.1063/1.4811791 |
| [28] |
GUO Y B, XU T, LI M. Atomistic calculation of internal stress in nanoscale polycrystalline materials[J]. Philosophical Magazine A, 2012, 92(24): 3064. DOI:10.1080/14786435.2012.685963 |
| [29] |
赵鹏越, 郭永博, 白清顺, 等. 基于微观结构的多晶Cu纳米压痕表面缺陷研究[J]. 金属学报, 2018, 54(7): 1053. ZHAO Pengyue, GUO Yongbo, BAI Qingshun, et al. Research of surface defects of polycrystalline copper nanoindentation based on microstructures[J]. Acta Metallurgica Sinica, 2018, 54(7): 1053. DOI:10.11900/0412.1961.2017.00411 |
| [30] |
赵鹏越, 郭永博, 白清顺, 等. 压痕位置对多晶铜纳米压痕变形机理的影响[J]. 哈尔滨工业大学学报, 2018, 50(7): 13. ZHAO Pengyue, GUO Yongbo, BAI Qingshun, et al. Influence of indentation position on the nanoindentation deformation mechanicsm of polycrystalline copper[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 13. DOI:10.11918/j.issn.0367-6234.201711061 |
| [31] |
WANG T H, FANG T H, KANG S H, et al. Creep characteristics of clamped Cu membranes subjected to indentation[J]. Japanese Journal of Applied Physics, 2008, 47(2R): 1019. |
| [32] |
ZHAO M, SLAUGHTER W S, LI M, et al. Material-length-scalecontrolled nanoindentation size effects due to strain-gradient plasticity[J]. Acta Materialia, 2003, 51(15): 4461. DOI:10.1016/S1359-6454(03)00281-7 |
| [33] |
LI X, WEI Y, LU L, et al. Dislocation nucleation governed softening and maximum strength in nano-twinned metals[J]. Nature, 2010, 464: 877. DOI:10.1038/nature08929 |
| [34] |
VO N Q, AVERBACK R S, BELLON P, et al. Yield strength in nanocrystalline Cu during high strain rate deformation[J]. Scripta Materialia, 2009, 61(1): 76. DOI:10.1016/j.scriptamat.2009.03.003 |
| [35] |
QU S, ZHOU H. Hardening by twin boundary during nanoindentation in nanocrystals[J]. Nanotechnology, 2010, 21(33): 335704-1. DOI:10.1088/0957-4484/21/33/335704 |
| [36] |
JIANG J, BRITTON T B, WILKINSON A J. Evolution of intragranular stresses and dislocation densities during cyclic deformation of polycrystalline copper[J]. Acta Materialia, 2015, 94: 193. DOI:10.1016/j.actamat.2015.04.031 |
| [37] |
KYSAR J W, GAN Y X, MORSE T L, et al. High strain gradient plasticity associated with wedge indentation into face-centered cubic single crystals: Geometrically necessary dislocation densities[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(7): 1554. DOI:10.1016/j.jmps.2006.09.009 |
| [38] |
PAN Z, RUPERT T J. Damage nucleation from repeated dislocation absorption at a grain boundary[J]. Computational Materials Science, 2014, 93: 206. DOI:10.1016/j.commatsci.2014.07.008 |
| [39] |
ZHANG J J, SUN T, HARTMAIER A, et al. Atomistic simulation of the influence of nanomachining-induced deformation on subsequent nanoindentation[J]. Computational Materials Science, 2012, 59: 14. DOI:10.1016/j.commatsci.2012.02.024 |
| [40] |
ZHOU K, LIU B, SHAO S, et al. Molecular dynamics simulations of tension-compression asymmetry in nanocrystalline copper[J]. Physics Letters A, 2017, 381(13): 1163. DOI:10.1016/j.physleta.2017.01.027 |
| [41] |
YEAP K B, ZSCHECH E, HANGEN U D, et al. Elastic anisotropy of Cu and its impact on stress management for 3D IC: Nanoindentation and TCAD simulation study[J]. Journal of Materials Research, 2012, 27(1): 339. DOI:10.1557/jmr.2011.323 |
| [42] |
REUBER C, EISENLOHR P, ROTERS F, et al. Dislocation density distribution around an indent in single-crystalline nickel: Comparing nonlocal crystal plasticity finite-element predictions with experiments[J]. Acta Materialia, 2014, 71: 333. DOI:10.1016/j.actamat.2014.03.012 |
| [43] |
LIU Y, VARGHESE S, MA J, et al. Orientation effects in nanoindentation of single crystal copper[J]. International Journal of Plasticity, 2008, 24(11): 1990. DOI:10.1016/j.ijplas.2008.02.009 |
 2019, Vol. 51
2019, Vol. 51


