航空工业、船舶制造业以及国防工业等作为国家“硬实力”的象征,现在已成为我国的战略核心领域.这些产业的发展对大型结构件的加工提出了更高的精度要求[1].研究表明,热误差对机床精度有重要影响[2],最高达到75%的加工件误差可由热误差引起[3],而热误差在龙门机床加工中的影响也是巨大的[4],运动轴热定位误差的产生是由于定位或传动元件因温度变化而产生变形[5].由于龙门加工中心的较长行程,其一般采用光栅尺定位,在加工时受机床内热源以及外部环境的影响, 光栅尺会发生温度变化,从而产生热变形,引起定位热误差[6].除加工中心外,结构件毛坯的热变形也对其加工精度有重要影响,因为其具有大型化的特点且材料热膨胀系数较高[7],并易受温度影响.因此,在加工、检测过程中,工件热变形也是十分重要的一项误差源.
通常解决这一问题的两种方法为恒温控制和自动在线检测.恒温控制通过建立恒温车间控制机床温度,减少热误差的产生;而自动在线检测通过自动对刀仪或者自动测头等装置实现对刀具或者工件尺寸的自动在线测量,并利用测试的误差数据自动修正加工程序,实现一定的补偿调整[8].虽然以上方法有一定效果,但也均有明显的缺点:恒温控制难以做到完全恒温,只能把温度控制在一定范围内;而自动检测受环境影响大,且降低了加工效率;另外,两者均存在的一个严重问题是设备费用昂贵,对成本影响大[9].相比之下,采用误差补偿方式来减小定位误差更加便捷经济且有效[10].
冯文龙等[11]采用对光栅尺各点温升量积分的方法,建立了光栅定位热误差模型,对落地镗床TK6920进行光栅尺定位热误差补偿,定位精度有明显提升,但其依赖于大量的传感器且没有进行实际加工故没有考虑工件热变形. Cao等[12]考虑工件的热变形,对干切滚齿机进行了热误差建模与补偿,有不错的实际加工效果.孙志超等[13]建立包含工件膨胀效应的车床主轴与进给轴综合热误差多元线性回归模型,有较好的模型预测精度与实际切削效果,但是其研究对象为利用滚珠丝杠定位的小型车床.总体而言,目前的热误差补偿研究中,虽然对于大型龙门加工中心及工件热变形均有分别考虑,但是数量较少,且缺乏综合的研究.
为了提高高速龙门加工中心加工大型结构件时的精度,本文以一台三轴龙门加工中心为实验平台,研究了在有较大工件热变形时,龙门加工中心的定位误差建模问题.并利用自主研制的外部补偿器通过实时温度和误差模型在线计算补偿值,利用数控系统的外部坐标系原点偏移功能对龙门加工中心的定位误差进行实时补偿[14-15],验证了模型的准确性与实用性.
1 机床定位误差检测与建模 1.1 误差检测实验本文从机床和工件两个方面研究大型结构件的加工误差,对其进行建模和补偿.研究对象是一台三轴龙门加工中心,如图 1所示,其X和Y进给轴均采用光栅尺进行定位,数控系统为FANUC 18i.
|
图 1 龙门加工中心示意图 Fig. 1 Schematic diagram of gantry machining center |
建模前先进行误差检测实验,采用激光干涉仪在不同温度下分两次测量龙门加工中心X和Y轴的定位误差.两坐标轴的测量行程分别为3 500、2 300 mm,为了建模的统一性,测量时将每个坐标轴的测量行程均分为10段进行.为了同步获得机床坐标轴的相关温度状态,预先在两个坐标轴的光栅尺旁布置温度传感器.第1次测量时,X和Y两坐标轴光栅尺的温度分别为32.2、33.8 ℃,第2次测量时两个温度值变为28.4、29.3 ℃,两次测量得到的定位误差数据如图 2所示.
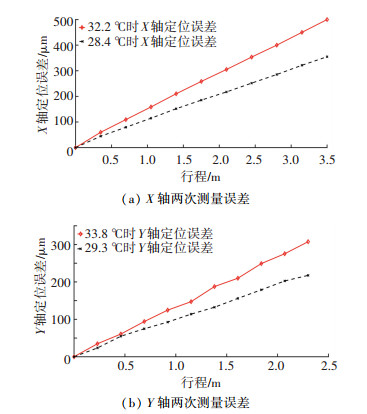
|
图 2 两坐标轴不同温度下的定位误差 Fig. 2 Positioning errors of each axis at different temperatures |
为了研究龙门机床的定位误差,首先对其进行热特性分析.机床产生热定位误差的原因是温度的变化使用于定位的光栅尺产生伸缩,影响了其刻度间距.温度变化主要来自两方面,首先是车间环境温度的影响;其次是加工时电机、轴承等发热部件向周围散热会造成附近区域的光栅尺温度升高.
光栅尺的定位误差是一个由冷态下的几何误差和温度变化造成的热误差两部分组成的复合误差,几何误差是建模基准采用温度下的定位误差,只与位置坐标相关;热误差是相对基准温度的温变引起的光栅尺变形造成的误差,与位置坐标和光栅尺的温度变化均相关.本文建模过程中,取第2次测量时两轴的定位误差为其几何误差,第1次测量时的误差为带有热误差的复合定位误差.因此,机床运动轴光栅尺的定位误差可以表示为
| $ {E_{{P_{\rm{m}}}}}\left( {p,{T_P}} \right) = {E_{{P_0}}}(p) + {E_{PT}}\left( {p,{T_P}} \right). $ | (1) |
式中:P为运动轴X或Y,p为运动轴P的坐标值,EPm(p, TP)为温度TP时的定位误差;EP0(p)为P轴的几何误差;EPT(p, TP)为温度TP时的热误差.
1.3 几何误差建模对于几何误差,考虑到模型的光滑性与稳定性等特点,采用三次样条插值的方法进行建模,光栅尺几何误差与其制造安装等很多因素有关,所以难以确定其边界条件,故拟合时采用非扭结边界条件.
若P轴光栅尺冷态误差EP0(p)与位置坐标p的拟合关系为S(p),则S(p)在每个测试区间[pi-1, pi]上均为三次多项式,由于每个轴都采集10个均匀的测试区间,则i=1, 2, …, 10,根据非扭结边界条件
| $ S_{0}^{\prime \prime \prime}(p)=S_{1}^{\prime \prime \prime}(p), S_{8}^{\prime \prime \prime}(p)=S_{9}^{\prime \prime \prime}(p). $ |
计算得到
| $ M_{0}=\left(M_{1}-\mu_{1} M_{2}\right) / \lambda_{1}, M_{10}=\left(M_{9}-\lambda_{9} M_{8}\right) / \mu_{9}. $ |
再由三弯矩基本方程,可得
| $ \left[\begin{array}{ccccc}{2} & {1} & {} & {} & {} \\ {\mu_{2}} & {2} & {\lambda_{2}} & {} & {} \\ {} & {\ddots} & {\ddots} & {\ddots} & {} \\ {} & {} & {\mu_{8}} & {2} & {\lambda_{8}} \\ {} & {} & {} & {1-f_{p}} & {2+f_{p}}\end{array}\right]\left[\begin{array}{c}{M_{1}} \\ {M_{2}} \\ {\vdots} \\ {M_{8}} \\ {M_{9}}\end{array}\right]=\left[\begin{array}{c}{6 d_{1}} \\ {6 d_{2}} \\ {\vdots} \\ {6 d_{8}} \\ {6 d_{9}}\end{array}\right]. $ |
式中:Mj=S″(pj)(j=0, 1, …, 10)是待定参数;由于激光干涉仪在坐标轴上均匀采集误差数据,所以同一坐标轴的步长h相等,则
| $ \mu_{k}=h_{k-1} /\left(h_{k-1}+h_{k}\right)=0.5; $ |
| $ \lambda_{k}=1-\mu_{k}=0.5 ; k=1,2, \cdots, 9; $ |
dk=EP0[pk-1, pk, pk+1]为EP0(p)的二阶均差;fP为坐标轴P的测量行程.
以Y轴为例展示建模结果,Y轴的冷态温度为29.3 ℃,表 1为简化处理后的三次样条插值参数,当i=1, 2, …, 10时,在区间[yi, yi+1]内,Y轴冷态误差EY0(y)的建模结果应为
| $ \begin{aligned} E_{Y 0}(y)=& S_{i}(y)=a_{Y i}\left(y-y_{i}\right)^{3}+b_{Y i}\left(y-y_{i}\right)^{2}+\\ & c_{Y i}\left(y-y_{i}\right)+d_{Y i} \end{aligned}. $ |
| 表 1 Y轴几何误差建模参数 Tab. 1 Geometric error modeling parameters of Y-axis |
Y轴的几何误差插值曲线见图 3.
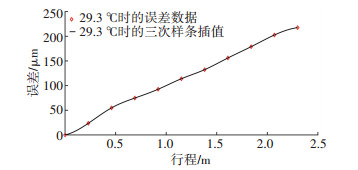
|
图 3 Y轴几何误差插值结果 Fig. 3 Geometric error interpolation result of Y-axis |
加工时若光栅尺温度与建模基准温度不一致,会产生热误差.其热误差即为受温度影响产生的变形量,与温度变化呈线性关系.故若取坐标起始点为光栅尺基准定位点,光栅尺温度均匀变化时其热误差可以表示为
| $ E_{P T}\left(p, T_{P}\right)=\Delta L=\alpha_{P_{\mathrm{g}}} L\left(T_{P}-T_{P 0}\right), $ | (2) |
光栅尺温度变化不均匀时热误差可以表示为
| $ E_{P T}\left(p, T_{P}\right)=\Delta L=\alpha_{P_{\mathrm{g}}} \int_{0}^{L}\left(T_{P}-T_{P 0}\right) \mathrm{d} p. $ | (3) |
式中:ΔL为光栅尺的热变形量,αPg为P轴光栅尺的线性热膨胀系数,L为光栅尺的长度,TP为加工时P轴光栅尺的实时温度,TP0为P轴几何误差建模时的温度.
由式(2)和(3)的光栅尺热误差模型可知,影响热误差大小的两个待定因素是其线性热膨胀系数和实时温度,下面将分别对其进行标定和建模.
1.4.2 光栅尺线性热膨胀系数标定由于光栅尺有玻璃和钢带等不同类别,需要对各坐标轴光栅尺的线性膨胀系数进行标定.利用第1次测量得到的复合定位误差数据进行光栅尺的标定.仍以Y轴为例展示标定过程,第1次测量Y轴定位误差时温度为33.8 ℃,此时的复合定位误差与冷态时的几何误差数据如图 4所示.
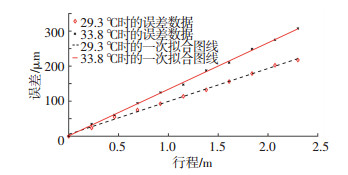
|
图 4 Y轴复合误差与几何误差 Fig. 4 Composite error and geometric error of Y axis |
根据对光栅尺热特性的分析,由式(1)得
| $ {E_{YT}}\left( {y,{T_Y}} \right) = {E_{Y{\rm{m}}}}\left( {y,{T_Y}} \right) - {E_{Y0}}(y) = {\alpha _{Y{\rm{g}}}}y\left( {{T_Y} - {T_{Y0}}} \right). $ | (4) |
由于两次实验均采集了多个坐标点,为了增加模型的可靠性,对两组数据进行一次拟合,如图 4所示,利用其拟合斜率进行计算,结合式(4)有
| $ {E_{YT}}\left( {y,{T_{Y1}}} \right) = \left( {{T_{Y1}} - {T_{Y0}}} \right){\alpha _{Y{\rm{g}}}}y = \left( {{k_{{T_{Y1}}}} - {k_{{T_{Y0}}}}} \right)y. $ |
式中:TY0、TY1分别为Y轴基准温度和标定测量时的温度,kTY0、kTY1则分别为两温度下定位误差的一次拟合斜率值.
因此,Y轴光栅尺线性热膨胀系数应为
| $ {\alpha _{Y{\rm{g}}}} = \left( {{k_{{T_{Y1}}}} - {k_{{T_{Y0}}}}} \right)/\left( {{T_{Y1}} - {T_{Y0}}} \right). $ |
标定得到两坐标轴光栅尺的线性热膨胀系数为
| $ {\alpha _{X{\rm{g}}}} = 10.8\mu {\rm{m}}/({\rm{m}} \cdot {}^ \circ {\rm{C}}),{\alpha _{Y{\rm{g}}}} = 8.6\mu {\rm{m}}/({\rm{m}} \cdot {}^ \circ {\rm{C}}). $ |
根据光栅尺线性热膨胀系数范围可以确定X轴应为钢带光栅尺,Y轴为玻璃光栅尺,同时可以由材料得到两光栅尺的各项热物性参数.
1.4.3 光栅尺温度预测模型为了便于研究光栅尺的实时温度,作如下假设:
1) 一段时间内,热源区域的影响可以看做均匀热流从距离热源最近的光栅尺表面进入,通过传导造成光栅尺局部温度的不均匀;
2) 由于热源的影响仅为光栅尺的局部区域,因此对整个光栅尺做无限长假设;
3) 由于光栅尺的温度变化主要来源于环境影响,因此忽略其对流和辐射的散热影响.
根据以上假设,可以得到热源影响时光栅尺内部的导热微分方程应为
| $ \frac{\partial^{2} T(l, \tau)}{\partial l^{2}}=\frac{1}{a} \frac{\partial T(l, \tau)}{\partial \tau}. $ |
在均匀热流时,应有初始条件:
| $ T(l, 0)=T_{\infty}. $ |
边界条件:
| $ -\lambda\left.\frac{\partial T(l, \tau)}{\partial l}\right|_{l=0}=q. $ |
式中,l为光栅尺上某位置与热流输入点的距离;τ为加热时间;T为瞬时温度;T∞为不受热流影响的初始温度;q为输入的热流密度;λ和a分别为导热系数和热扩散率,是光栅尺的热物性参数与材料种类有关.
应用分离变量法,可得上述热微分方程的解为
| $ T(l, \tau)=T(l, 0)+\frac{2 q}{\lambda} \sqrt{a \tau} \text { ierfc }(l / \sqrt{4 a \tau}). $ | (5) |
其中ierfc为高斯误差补函数的一次积分.
本次实验机床的X轴与Y轴仅有一端受热源影响.如图 5所示,以Y轴为例,Y轴需承载有一定宽度的Z轴滑台,其光栅读数头在Z轴滑台左侧,而Y轴丝杠螺母在滑台右侧,因此,Y轴光栅尺与其丝杠长度并不匹配,对其造成热影响的为游动端轴承.与之类似,受工作台长度影响,对X轴光栅尺造成热影响较大的为电机和固定端轴承.

|
1—光栅尺末端;2—Y轴游动端轴承;3—光栅尺起始端、传感器T2布置处;4—电机及固定端轴承;5—传感器T1布置处;6—Z轴滑台及主轴 图 5 Y轴结构示意图 Fig. 5 Schematic diagram of structure for Y axis |
分别在光栅尺最接近热源处和不受热源影响处布置两个温度传感器T1和T2,结合式(5)有
| $ q=\lambda \frac{T_{1}-T_{2}}{2 \sqrt{a \tau} \operatorname{ierfc}\left(\frac{0}{\sqrt{4 a \tau}}\right)}=\lambda \frac{T_{1}-T_{2}}{2 \sqrt{a \tau} \operatorname{ierfc}(0)}. $ | (6) |
将式(6)代入式(5)可得任意位置的温度
| $ T(l, \tau)=T_{2}+\frac{T_{1}-T_{2}}{\operatorname{ierfc}(0)} \text { ierfc }\left(\frac{l}{\sqrt{4 a \tau}}\right). $ |
若取光栅尺起始点与热源(图 5(a)中3和5)的距离为l1,则有光栅尺的实时温度
| $ T_{P}=T(p, \tau)=T_{2}+\frac{T_{1}-T_{2}}{\text { ierfc }(0)} \text { ierfc }\left(\frac{\left|p-l_{1}\right|}{\sqrt{4 a \tau}}\right). $ | (7) |
将实时温度模型式(7)代入光栅尺热误差模型式(3),即可得到光栅尺的实时热误差.
2 考虑工件热变形的综合误差建模加工时工件毛坯也会受到环境等因素的影响造成与设计加工的温度不一致,同样会造成毛坯热变形影响加工时的定位精度.与光栅尺类似,工件温度变化产生的热变形应为
| $ {E_{\rm{w}}}\left( {p,{T_{\rm{w}}}} \right) = {\alpha _{\rm{w}}}p\left( {{T_{\rm{w}}} - {T_{\rm{b}}}} \right). $ |
式中:αw为工件的热膨胀系数;Tb为工件设计采用的基准温度,一般为20 ℃.
本文针对的是大型结构件的加工,由于结构件和光栅尺均是由具有热胀冷缩物性的材料加工而成,以实验机床为例其加工的是大型扭力臂,材料为球墨铸铁,热膨胀系数13.2 μm/(m· ℃),要比光栅尺大,即αw > αPg,故机床误差会抵消一部分工件热变形,但是基于其较大的基础结构,依然会有较大的误差.
如图 6(a)所示,若加工两个在基准温度下相距为d的孔,当加工温度为基准温度时,光栅尺和工件均没有产生相对长度变化,此时没有加工误差;但当加工温度和基准温度不一致时,如图 6(b)所示,由于工件具有较大的热膨胀系数,其热变形量要比机床光栅尺大,综合工件和机床光栅尺两者的伸缩量,可以得到此时的加工误差应为
| $ E\left( {p,{T_P}} \right) = {E_{P{\rm{m}}}}\left( {p,{T_P}} \right) - {E_{\rm{w}}}\left( {p,{T_P}} \right). $ |
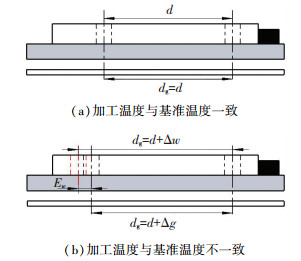
|
图 6 工件热变形对加工的影响 Fig. 6 Effect of workpiece thermal deformation on machining |
综上,利用图 7建模过程可以对龙门加工中心的3个坐标轴进行考虑工件热变形的综合误差建模.
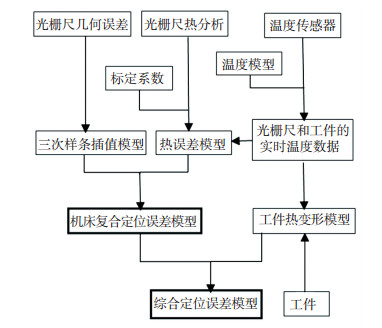
|
图 7 综合误差建模流程 Fig. 7 Algorithm flowchart of comprehensive error model |
在龙门加工中心上进行补偿验证实验.误差补偿是移动刀具或工件,使刀具和工件之间在机床的逆方向上产生一个大小与误差相近的相对运动而实现的.用于实验的龙门加工中心基于FANUC 18i数控系统并配有内置网络接口,其通讯功能是基于TCP/IP协议实现的.误差补偿器通过调用数控系统开放的一系列应用程序编程接口函数(FOCAS),便可以通过TCP/IP接口对机械坐标数据、进给速度等CNC数据进行实时读取.在补偿过程中,自主研制的补偿系统通过温度监测模块获得光栅尺和工件的实时温度数据,结合读取到的坐标轴实时位置信息,通过计算处理模块利用上述模型计算得到误差值,将其反向后作为补偿值.通过继续调用FOCAS的相关函数,将补偿值实时写入机床PLC的数据区.在实际补偿中,CNC会在每个PLC扫描周期内读取写入的补偿数据,然后基于外部坐标系原点偏移功能[11],对加工坐标系的零点进行实时更新,形成新的坐标系,达到误差实时补偿的目的,补偿过程见图 8.
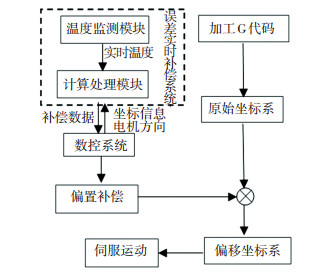
|
图 8 补偿原理 Fig. 8 Schematic diagram of error compensation |
补偿效果的验证分为两步进行,首先验证不考虑工件热变形的复合误差模型,在不考虑工件热变形时对比复合模型补偿前后的误差数据验证其对机床的补偿能力,再用激光干涉仪模拟工件热变形,证明其无法补偿有工件热变形的加工情况;然后,验证考虑工件热变形的综合误差模型的补偿效果,先在同样用激光干涉仪模拟工件热变形时进行误差补偿,验证补偿效果,再进行实际加工实验验证其实际应用能力.
3.2.1 复合误差模型验证验证不考虑工件热变形的复合误差模型时,首先只针对机床,用复合误差模型进行补偿,通过激光干涉仪检测复合误差模型补偿前后的机床误差.在X轴和Y轴分别为30.5 ℃和31.2 ℃时,机床两个坐标轴补偿前后的测量结果如图 9中曲线1, 2所示.此时X轴补偿前后的最大误差分别为431、16.2 μm,而Y轴为253.1、13.3 μm.可以看出在不考虑工件热变形时复合误差模型对机床误差的预测具有很高的精度.
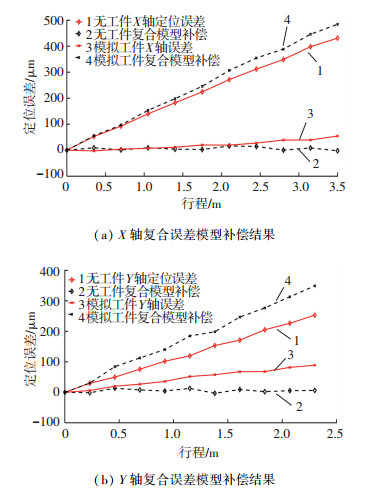
|
图 9 复合误差模型补偿结果 Fig. 9 Compensation results of compound error model |
然后通过激光干涉仪的自动温度补偿功能模拟加工时的工件热变形,在只用复合误差模型补偿时,机床3个坐标轴补偿前后的测量结果如图 9中曲线3, 4所示.此时X轴补偿前后的最大误差分别为54.6、484.4 μm,而Y轴为88.9、349.1 μm.可以看出,补偿前后均具有较大误差,且补偿后误差更大,这一结果很好地证明了前文中“机床误差会抵消一部分工件热变形”的分析,因此,在大型结构件的加工中不能使用复合误差模型进行补偿.
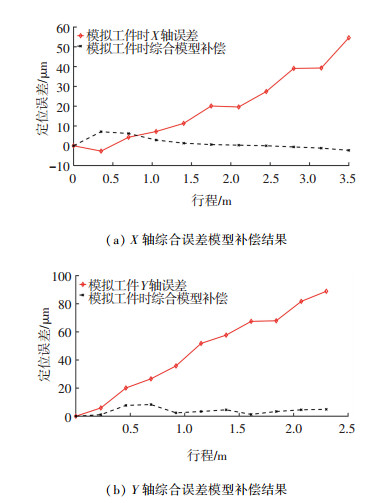
3.2.2 综合误差模型验证仍通过激光干涉仪的自动温度补偿功能模拟加工时的工件热变形,用考虑工件热变形的综合误差模型补偿机床,机床坐标轴补偿前后的测量结果如图 10所示.此时X轴补偿前后的最大误差分别为54.6、7.1 μm,而Y轴为88.9、8.3 μm,其精度分别提高了87%和91%.可以看出,在有工件热变形时综合误差模型具有很好的补偿效果.
|
图 10 综合误差模型补偿结果 Fig. 10 Compensation results of comprehensive error model |
在综合模型补偿下,对扭力臂进行实际加工实验,加工32个均布在扭力臂上表面直径为30 mm的孔,加工过程如图 11所示.

|
图 11 实际加工示意图 Fig. 11 Schematic diagram of machining process |
加工完成后,将工件放入三坐标测量机的恒温室中,待温度稳定到20 ℃时,利用三坐标测量机检测各孔的定位误差,由于数据较多仅将极值放入表 2中,其中,定位直径ϕ如图 11(b)中所示.在季节更替时,由于环境温度的上升实验机床已经出现加工不合格的现象,实际生产中采用调整加工程序的方式保证加工精度.而由于实验时的温度已经远超季节更替时的温度,考虑到大型扭力臂价格较高,并不能采用实际加工的方式来检验机床在实验时的实际加工误差.但可以确定,其误差超过了定位直径ϕ的要求公差(±0.046 mm), 因此,补偿后精度至少提高了1-47.61%=52.39%.
| 表 2 加工补偿结果 Tab. 2 Machining compensation results |
通过以上实验,再次验证了温度造成的光栅尺和工件毛坯的热变形是引起大型结构件加工误差的主要原因,同时,上述综合模型能够在考虑光栅尺和工件热变形的情况下准确预测加工过程中的定位误差,具有良好的实际补偿效果.
4 结论1) 分析了龙门加工中心的热特性,对X和Y两坐标轴的几何误差和热误差进行了分别建模,得到机床各坐标轴的复合定位误差模型.
2) 基于大型结构件体积大、热膨胀系数高的特点,分析了工件热变形对实际加工的影响,建立了考虑工件热变形的综合误差模型.
3) 通过自主研制的误差补偿系统,利用数控系统的外部坐标系原点偏移功能进行实时补偿.激光干涉仪检测表明复合误差模型可以很好地预测龙门加工中心的误差,但并不适用于有工件热变形的加工情况.激光干涉仪检测和实际加工均表明综合误差模型对加工中存在较大工件热变形的情况具有很好的补偿效果,能够使大型结构件的加工定位精度提高52%以上.
| [1] |
黄晓明, 孙杰, 李剑峰. 基于刚度与应力演变机制的航空整体结构件加工变形预测理论建模[J]. 机械工程学报, 2017, 53(9): 201. HUANG Xiaoming, SUN Jie, LI Jianfeng. Mathematical modeling of aeronautical monolithic component machining distortion based on stiffness and residual stress evolvement[J]. Journal of Mechanical Engineering, 2017, 53(9): 201. DOI:10.3901/JME.2017.09.021 |
| [2] |
王海同, 李铁民, 王立平, 等. 机床热误差建模研究综述[J]. 机械工程学报, 2015, 51(9): 119. WANG Haitong, LI Tiemin, WANG Liping, et al. Review on thermal error modeling of machine tools[J]. Journal of Mechanical Engineering, 2015, 51(9): 119. DOI:10.3901/JME.2015.09.119 |
| [3] |
MAYR J, JEDRZEJEWSKI J, UHLMANN E, et al. Thermal issues in machine tools[J]. CIRP Annals-Manufacturing Technology, 2012, 61(2): 771. DOI:10.1016/j.cirp.2012.05.008 |
| [4] |
GOMEZ-ACEDO E, OLARRA A, CALLE L N L D L. A method for thermal characterization and modeling of large gantry-type machine tools[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(9/10/11/12): 875. DOI:10.1007/S00170-011-3879-0 |
| [5] |
TAN B, MAO X, LIU H, et al. A thermal error model for large machine tools that considers environmental thermal hysteresis effects[J]. International Journal of Machine Tools & Manufacture, 2014, 82/83(7): 11. DOI:10.1016/j.ijmachtools.2014.03.002 |
| [6] |
ZHANG D, YANG J, MA C, et al. Experiment-based thermal error modeling method for dual ball screw feed system of precision machine tool[J]. International Journal of Advanced Manufacturing Technology, 2016, 82(9/10/11/12): 1693. |
| [7] |
LI J G, WANG S Q. Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: Recent advances[J]. International Journal of Advanced Manufacturing Technology, 2017, 89(1/2/3/4): 997. DOI:10.1007/S00170-016-9066-6 |
| [8] |
HE L Y, GUO Y B, HUANG H, et al. The technique of online measurement and data processing for aspheric machining[J]. Advanced Materials Research, 2010, 97/98/99/100/101: 4313. |
| [9] |
CHO M W, KIM G H, SEO T I, et al. Integrated machining error compensation method using OMM data and modified PNN algorithm[J]. International Journal of Machine Tools & Manufacture, 2006, 46(12): 1417. DOI:10.1016/j.ijmachtools.2005.10.002 |
| [10] |
YANG J, YUAN J, NI J. Thermal error mode analysis and robust modeling for error compensation on a CNC turning center[J]. International Journal of Machine Tools & Manufacture, 1999, 39(9): 1367. |
| [11] |
冯文龙, 黄奕乔, 拓占宇, 等. 基于温度积分方法的大型数控机床光栅定位热误差建模及实时补偿[J]. 上海交通大学学报, 2016, 50(5): 710. FENG Wenlong, HUANG Yiqiao, TUO Zhanyu, et al. Modeling of thermally induced grating positioning error of large machine tools based on temperature integral method and real-time compensation[J]. Journal of Shanghai Jiaotong University, 2016, 50(5): 710. |
| [12] |
CAO H, ZHU L, LI X, et al. Thermal error compensation of dry hobbing machine tool considering workpiece thermal deformation[J]. International Journal of Advanced Manufacturing Technology, 2016, 86(5/6/7/8): 1. |
| [13] |
孙志超, 侯瑞生, 陶涛, 等. 数控车床综合热误差建模及工程应用[J]. 哈尔滨工业大学学报, 2016(1): 107. SUN Zhichao, HOU Ruisheng, TAO Tao, et al. Comprehensive thermal error modeling for NC lathe in engineering application[J]. Journal of Harbin Institute of Technology, 2016(1): 107. |
| [14] |
FENG W L, YAO X D, AZAMATA, et al. Straightness error compensation for large CNC gantry type milling centers based on B-spline curves modeling[J]. International Journal of Machine Tools & Manufacture, 2015, 88: 165. |
| [15] |
姜辉, 杨建国, 李自汉, 等. 基于误差分解的数控机床热误差叠加预测模型及实时补偿应用[J]. 上海交通大学学报, 2013, 47(5): 744. JIANG Hui, YANG Jianguo, LI Zihan, et al. Application of real time compensation with combinative thermal error prediction model based on error separation on CNC machine tools[J]. Journal of Shanghai Jiaotong University, 2013, 47(5): 744. |
 2019, Vol. 51
2019, Vol. 51


