2. 重庆邮电大学 先进制造工程学院,重庆 400065
2. School of Advanced Manufacturing Engineering, Chongqing University of Posts and Telecommunications, Chongqing, 400065, China
热误差作为精密数控机床最主要的误差来源,其误差占比最高达到70%,减小热误差的影响是目前提高机床精度的一种重要方法[1-2].热误差补偿方法一般分为硬件消除及软件补偿.软件补偿是建立一个准确的热误差预测模型,并通过该模型产生一个补偿误差去实时抵消原热误差,从而达到减少热误差的目的,相对于硬件消除更加经济、高效,因而获得了更加广泛的应用.
软件补偿法的难点在于建立实时准确的热误差预测模型,国内外学者对此做了大量的研究.主要的热误差建模方法有:多元线性回归(MLR)[3]、灰色预测模型(GM)[4-5]、最小二乘支持向量机(LS-SVM)[6-7]、人工神经网络(ANN)[8-9]及混合预测模型[10-12]等.上述模型均取得了一些不错的预测及补偿效果,但是却很少涉及不同工况下机床热误差预测模型的泛化性能的研究,或者出现泛化性能不佳的情况. Yang Hong等人研究发现[13],导致预测模型稳健性差的主要原因是机床的热误差变化普遍滞后于温度变化的现象,即伪滞后效应.但是如今却很少有考虑伪滞后效应的热误差建模方法,其中基于时间序列的分布滞后模型[14-15],预测精度及鲁棒性较好,但是仍未考虑前后不同时刻热误差之间的影响,有待进一步研究.因此,本文通过研究机床的伪滞后现象,利用新陈代谢原理建立了基于遗传算法及最小二乘支持向量机的热误差伪滞后预测模型,以前一时刻的关键点温升及热误差为输入,预测后一时刻的热误差.验证了热误差伪滞后预测模型的准确性,以及适用于不同工况下热误差预测模型的实用性.
1 热误差伪滞后建模原理及流程大量实验数据表明,由于零部件之间热量的传递过程及材料的导热性能的不同,机床的热误差变化总是滞后于温度变化,导致无法对热误差进行实时、准确的预测及补偿.为此,本文通过对机床热误差伪滞后现象进行分析研究,获得了机床典型工况下的热误差伪滞后平均滞后时间,通过对滞后数据进行迭代修正,改善了输入与输出之间的不对称映射,得出了预测精度高、泛化性能强的机床热误差伪滞后预测模型.
1.1 遗传算法遗传算法是美国Michigan大学的Holland教授基于自然界遗传机制和生物进化论提出的一种并行随机搜索最优化方法.其基本思想是在遗传进化过程中,适应度大的个体基因被保留,而适应度差的个体基因被淘汰,使得新的个体既继承了上一代的信息,又优于上一代.遗传算法的操作过程主要为:1)初始化种群;2)染色体编码;3)确定适应度函数;4)进行遗传操作,选择、交叉及变异;5)根据终止条件判断进化是否结束.遗传算法具有全局搜索的特点,能够避免陷入局部最优,是一种快速、准确的启发式寻优算法.
1.2 最小二乘支持向量机支持向量机是由Vapnik[16]首先提出的一种基于结构风险最小化原理的机器学习算法,主要解决小样本、贫信息、高维数、非线性等实际问题. Suykens[17]提出的最小二乘支持向量机是其最主要的一种算法变种,该方法采用最小二乘线性系统作为损失函数,将不等式约束改为等式约束,使得算法求解速度更快、泛化性能更强,已广泛应用于分类及回归等问题.
LS-SVM建模问题可以描述为求解如下问题:
| $ \left\{ {\begin{array}{*{20}{l}} {\min J\left( {\mathit{\boldsymbol{\omega }},{\xi _i}} \right) = \frac{1}{2}{{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + \gamma \frac{1}{2}\sum\limits_{i = 1}^n {\xi _i^2} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}{y_i} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{\mathit{\boldsymbol{x}}_i}} \right) + b + {\xi _i}\quad i = 1, \cdots ,n} \end{array}} \right. $ |
式中:J为结构风险最小化函数; xi为输入量; yi为目标值; ξi为误差变量,ξi∈ R; $φ$(·)为映射到核空间的函数,可将低维空间的函数映射到h维核空间; ω为权矢量,ω∈Rh; γ为可调参数; b为偏差量.
引入拉格朗日函数(最优解为拉格朗日函数的鞍点)
| $ \begin{array}{l} L = \frac{1}{2}{\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \gamma \frac{1}{2}\sum\limits_{i = 1}^n {\xi _i^2} - \sum\limits_{i = 1}^n {{\alpha _i}} \left( {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{\mathit{\boldsymbol{x}}_i}} \right) + } \right.\\ \;\;\;\;\;\;b + {\xi _i} - {y_i}) \end{array} $ |
式中:αi(i=1, 2, …, n)为拉格朗日乘子.根据极值存在的必要条件(拉格朗日函数在鞍点处的w和b的梯度为0),得到
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial L}}{{\partial \omega }} = 0 \to \omega = \sum\limits_{i = 1}^n {{\alpha _i}} \varphi \left( {{\boldsymbol{x }_i}} \right),}\\ {\frac{{\partial L}}{{\partial b}} = 0 \to \sum\limits_{i = 1}^n {{\alpha _i}} = 0,}\\ {\frac{{\partial L}}{{\partial {\xi _i}}} = 0 \to {\alpha _i} = \gamma {\xi _i},\quad i = 1, \cdots n,}\\ {\frac{{\partial L}}{{\partial {\alpha _i}}} = 0 \to {y_i} = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b + {\xi _i},i = 1, \cdots n,} \end{array}} \right. $ |
消去式中的ω和ξi,得到
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} 0&1& \ldots &1&{}\\ 1&{K\left( {{x_1},{x_1}} \right) + 1/\gamma }& \cdots &{K\left( {{x_1},{x_n}} \right)}&{}\\ \vdots & \vdots &{}& \vdots &{}\\ 1&{K\left( {{x_n},{x_1}} \right)}& \cdots &{K\left( {{x_n},{x_n}} \right) + 1/\gamma }&{} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} b\\ {{\alpha _1}}\\ \vdots \\ {{\alpha _n}} \end{array}} \right] = \\ \;\;\left[ {\begin{array}{*{20}{c}} 0\\ {{y_1}}\\ \vdots \\ {{y_n}} \end{array}} \right]. \end{array} $ |
根据Mercer条件,使用核函数K(x, xi), LS-SVM回归建模可表示为
| $ f(x) = \sum\limits_{i = 1}^n {{\alpha _i}} K\left( {\boldsymbol{x },{\boldsymbol{x }_i}} \right) + b $ |
式中:x为输入量; xi为支持向量; αi为拉格朗日乘子,即支持向量的系数; b为偏差量.
核函数K(x, xi)为满足Mercer条件的任意对称函数.本文采用径向基核函数(高斯核函数):
| $ K\left( {{\boldsymbol{x }},{{\boldsymbol{x }}_i}} \right) = \exp \left( {\frac{{ - {{\left\| {{\boldsymbol{x }} - {{\boldsymbol{x }}_i}} \right\|}^2}}}{{2{\sigma ^2}}}} \right) $ |
式中:σ为宽度参数; ‖·‖2为欧氏距离的平方.
1.3 新陈代谢新陈代谢是一种常见的生物学概念,原指机体与机体内环境之间的物质和能量交换以及生物体内物质和能量的自我更新过程.其中心思想是利用新的数据替换已经老化的数据,实现数据的实时更新,保证结果的动态适应性.李永祥等人[4]利用灰色新陈代谢模型对机床热误差进行了预测,相比于传统灰色模型获得了更加精确的预测结果.
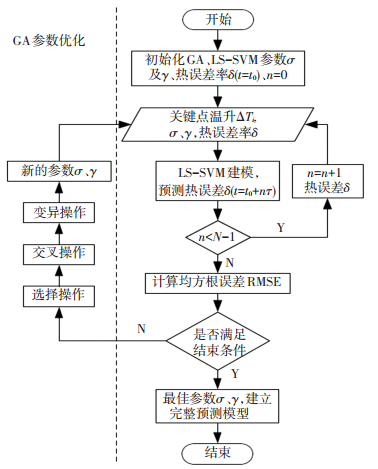
1.4 热误差伪滞后预测建模流程考虑到前一时刻热误差可能对当前时刻热误差产生的影响以及机床普遍存在的伪滞后效应,假设后一时刻的机床热误差是前一时刻关键点的温升及热误差的共同作用的结果.因此,通过初始化第一时刻(t1=t0)的热误差并结合关键点温升,计算出下一时刻(t2=t0+τ)的热误差,然后利用计算出的t2时刻的热误差及温升预测t3(t3=t0+2τ)时刻的热误差,以此类推,直到t=t0+(N-1)τ.基于新陈代谢原理的热误差伪滞后建模流程如图 1所示.
|
图 1 热误差伪滞后预测模型建模流程 Fig. 1 Modeling procedure of thermal error pseudo-hysteresis prediction model |
为验证本文所提出的热误差建模方法的可行性及有效性,以卧式数控加工中心THM6380为对象,对机床的的热误差进行伪滞后建模.具体流程如下:
为准确获取机床的温度场分布及热误差信息,本文采用Fluke公司的PT100温度传感器及Fluke2638A 20通道温度采集器测量机床主要部位(如主轴、主轴箱、电机及床身等)的温度场信息.以API主轴测试系统测量机床主轴的三向定位误差,实验流程依照《ISO 230-3-2012, Test Code for Machine Tools》进行.其中温度传感器的布置按照以下准则选取:1)传感器尽量覆盖所有激励热源及最大热变形处;2)同一激励热源处测点均匀布置,但距离不宜过近;3)对于难以测量的激励热源,在不影响机床性能的前提下可钻孔测温,否则采用近似处理,如以流过该热源处的液压油的温度替代.温度传感器布置如图 2所示,其中T1-T5位于主轴前端,T8-T10位于主轴后轴承端盖处,T6-T7及T11-T13位于主轴箱,T14-T16位于立柱,T17-T18位于床身,T19及T20分别测量工作台及环境温度.

|
图 2 机床测点分布图 Fig. 2 Layout of measuring points |
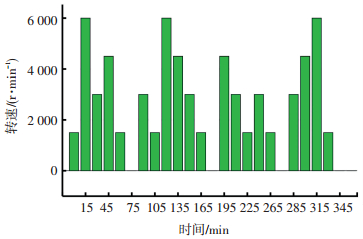
为体现支持向量机对小样本数据处理的优势,实验数据每隔5 min采集一次.设计4组热误差实验,分别为测量机床从停机状态开始,以转速为2 000 r/min、4 000 r/min、6 000 r/min连续空载运行6 h、6 h、4.5 h,然后停机,以混合转速连续空载运行6 h,然后停机.混合转速设计图谱如图 3所示.
|
图 3 混合转速图谱 Fig. 3 Mixed rotating speed distribution |
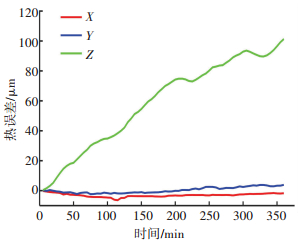
在机床运转过程中,实时采集各测点温度Ti(i=1, 2, …, 20)及热误差δX、δY和δZ,同一时刻采集的温度和热误差数据为一组样本序列,共采集了270组.以混合转速实验数据为例,采集的测点温升及热误差数据分别如图 4、图 5所示.由图 5可知,Z轴的热误差是其余两轴的10倍以上,由于篇幅有限,本文仅以Z轴热误差为预测目标进行热误差伪滞后建模.

|
图 4 测点温升曲线 Fig. 4 Measuring points temperature rising curve |
|
图 5 热误差曲线 Fig. 5 Thermal error curve |
由图 4可以看出从机床运转开始,各部件的温升快慢各有不同,轴承作为机床的最大热源,使得主轴轴承端盖处温升最快,其次是主轴箱及主轴,立柱、床身及工作台距离热源较远,温度变化较小.但由于位于同一零部件中的温升变化具有极大的相似性,为避免各测点间的多重共线性带来预测精度下降的情况,必须进行温度测点的优化选择.本文采用系统聚类及灰色关联度的方法进行测点的优化选择.最终选择的关键温度测点为:Ti(i=2,7, 8,18),分别位于主轴前端、主轴后轴承端盖以及床身处.对比具有最大灰色关联度的测点T8温升及Z轴热误差可以看出,在两曲线各拐点处热误差变化始终滞后于温升变化,由此说明机床存在伪滞后现象.因此,确定机床的热误差滞后时间便是建立准确预测模型的关键.
2.2 建立热误差伪滞后预测模型 2.2.1 建立热误差预测模型以混合转速的71组热误差实验数据作为训练集,对预测模型LS-SVM的径向基核函数参数σ和可调参数γ进行寻优.设置遗传算法初始种群为20,迭代数为250,过高的σ会导致过学习状态,因此设置参数的范围均为{0, 100},采用实数编码,以轮盘赌的方式进行个体选择,交叉概率为0.9,以单点方式进行交叉,变异概率为0.01,并采用K折交叉验证(K-fold Cross Validation, K-CV)寻优最佳参数σ、γ.交叉验证即将原始数据分为K组(一般是均分),然后将每个子集分别作一次验证集,其余K-1组子集作为训练集,如此得到K个模型,以验证集的回归均方误差的平均值作为此K-CV下的性能指标,此处采用5折交叉验证对数据集进行训练.最终的优化结构参数σ, γ分别为99.998、0.000 286 1.
2.2.2 确定热误差滞后时间采用不同的热误差滞后时间,以优化后的LS-SVM对各实验工况进行热误差预测.对比预测结果选择出具有最小均方根误差的预测模型,此时预测模型的滞后时间为相应工况下的最佳滞后时间.最后对各工况下的滞后时间进行算术平均,以此作为机床的热误差平均滞后时间.
由于机床的采样间隔为5 min,因此滞后时间的设置只能是采样间隔的整数倍.由此通过优化后的LS-SVM预测各工况下的热误差,其均方根误差如表 1所示.
| 表 1 不同转速不同滞后时间下的预测均方根误差RMSE Tab. 1 Predicting RMSE at different rotating speed with different lag time |
由表 1可知,随着滞后时间的增加,各工况预测热误差的RMSE均呈现出先减小后增大的趋势,不同工况下的热误差滞后时间也有所不同.当转速为2 000 r/min、4 000 r/min及6 000 r/min时,最佳预测滞后时间分别为10 min、5 min、10 min,其算术平均值为8.125 min,由于滞后时间只能是采样间隔的整数倍,因此机床的平均滞后时间取为10 min.以10 min作为机床热误差滞后时间,建立伪滞后预测模型,由此可得预测模型参数,αi为拉格朗日乘子,即支持向量系数,如表 2所示,b=-51.426 9,LS-SVM热误差伪滞后预测模型为
| $ f(x) = \sum\limits_{i = 1}^n {{\alpha _i}} \exp \left( { - 0.0001{{\left\| {x - {x_i}} \right\|}^2}} \right) - 51.4269. $ |
| 表 2 LS-SVM模型参数αi Tab. 2 Parameter αi of LS-SVM model |
为验证热误差伪滞后模型的准确性及假设条件的正确性,设置以下对比试验模型:
1) 试验模型1:以当前时刻的机床关键点温升为输入,利用GA-LSSVM进行参数寻优,遗传算法的初始化参数与热误差伪滞后模型相同,对机床热误差进行预测.
2) 试验模型2:以前一时刻的机床关键点温升为输入,利用GA-LSSVM进行参数寻优,遗传算法的初始化参数与热误差伪滞后模型相同,对机床热误差进行预测.
为评价模型的预测性能,本文主要采用最大残差、残差范围、均方根误差RMSE及决定系数R2等评价标准对预测性能进行评价,均方根误差及决定系数公式分别如下所示:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{RMSE}} = \sqrt {\sum\limits_{i = 1}^n {\delta _i^2} /(n - 1)}, \\ {R^2} = \frac{{{{\left( {n\sum\limits_{i = 1}^n {{y_i}} {y_i} - \sum\limits_{i = 1}^n {{y_i}} \sum\limits_{i = 1}^n {{y_i}} } \right)}^2}}}{{\left( {n\sum\limits_{i = 1}^n {\bar y_i^2} - {{\left( {\sum\limits_{i = 1}^n {{{\bar y}_i}} } \right)}^2}} \right)\left( {n\sum\limits_{i = 1}^n {y_i^2} - {{\left( {\sum\limits_{i = 1}^n {{y_i}} } \right)}^2}} \right)}}. \end{array} $ |
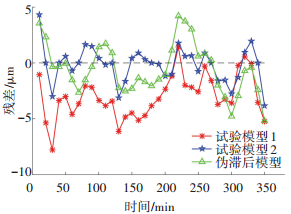
利用以上2种试验模型及热误差伪滞后模型进行混合转速热误差预测,预测结果如图 6及表 3所示.
|
图 6 混合转速时预测残差 Fig. 6 Predicting residual error at mixed rotating speed |
| 表 3 混合转速时预测热误差的精度对比 Tab. 3 Comparison of predicting thermal error accuracy at mixed rotating speed |
由图 6及表 3可知,3种预测模型均能较好地对热误差进行预测,其中试验模型2的最大残差e、残差范围R及均方根误差RMSE均为最小,决定系数R2最大,因此预测性能最好.其次是伪滞后模型,试验模型1的预测性能最差.
结果表明:
1) 以前一时刻的关键点温升及热误差为输入来预测下一时刻的热误差的方法是正确的,机床存在热误差伪滞后现象.
2) 伪滞后模型预测精度低于试验模型2,是采用新陈代谢方式进行预测热误差的结果,新陈代谢以预测热误差作为输入之一,相比于只采用测量温升增加了额外的输入误差,因此预测结果稍差.
3.2 泛化性能对比分析泛化性能的优良是评价预测模型好坏的重要因素,对于模型是否具有普遍适用性具有决定性作用.良好的预测模型往往具有较高的泛化性能.以上述3种预测模型对恒定转速为2 000 r/m、4 000 r/m的热误差进行预测,预测结果如图 7、图 8及表 4所示.

|
图 7 2 000 r/m时预测残差 Fig. 7 Predicting residual error at speed of 2 000 r/m |

|
图 8 4 000 r/m时预测残差 Fig. 8 Predicting residual error at speed of 4 000 r/m |
| 表 4 不同转速下的预测模型泛化性能对比 Tab. 4 Comparison of the generalization performance at different rotating speed |
由图 7、图 8及表 4可知,相比于预测自身热误差,预测不同转速热误差时各预测模型的预测精度均有所下降,但伪滞后模型的预测精度下降幅度最小,且其预测热误差的最大残差e、残差范围R及均方根误差RMSE均为最小,决定系数R2最大,因此泛化性能最好.
结果表明:
1) 2 000 r/m时的伪滞后模型的预测效果优于4 000 r/m,最大残差为2.720 0 μm,均方根误差为1.749 5 μm,决定系数为0.997 6.这是由于伪滞后模型的滞后时间更接近2 000 r/m时的滞后时间,因此预测效果更好.
2) 伪滞后模型的泛化性能优于试验模型1及试验模型2,说明了后一时刻的热误差是前一时刻关键点温升及热误差的共同作用的结果.输入中热误差的加入弥补了以关键点温升代表整机温度场造成的信息缺失,使得预测模型更加接近于真实热误差模型.
4 结论1) 通过实验研究了机床的伪滞后效应,计算出了机床的热关键点及典型工况下的平均滞后时间.
2) 以遗传算法优化最小二乘支持向量机的结构参数σ和γ,并通过采用新陈代谢的方式将预测热误差及实测关键点温升作为伪滞后模型的输入,获得了具有精度高、泛化性能强的热误差预测模型,使得机床热误差降低了90%以上.
3) 通过对比采用不同输入的热误差预测模型,得出了机床热误差是前一时刻关键点温升及热误差综合作用的结果,证明了本文提出的假设的正确性.
4) 本文的热误差建模方法为时间序列建模提供了参考,所提建模方法及结论在THM6380卧式加工中心上得到了验证,针对不同机床进行应用分析以及实际切削过程中的热误差分离及建模将是下一步研究的重点.
| [1] |
BRYAN J. International status of thermal error research (1990)[J]. CIRP Annals - Manufacturing Technology, 1990, 39(2): 645. DOI:10.1016/S0007-8506(07)63001-7 |
| [2] |
PAHK H J, LEE S W. Thermal error measurement and real time compensation system for the CNC machine tools incorporating the spindle thermal error and the feed axis thermal error[J]. International Journal of Machine Tools & Manufacture, 2002, 20(7): 487. |
| [3] |
李逢春, 王海同, 李铁民. 重型数控机床热误差建模及预测方法的研究[J]. 机械工程学报, 2016, 52(11): 154. LI Fengchun, WANG Haitong, LI Tiemin. Research on thermal error modeling and prediction of heavy CNC machine tools[J]. Journal of Mechanical Engineering, 2016, 52(11): 154. DOI:10.3901/JME.2016.11.154 |
| [4] |
李永祥, 杨建国. 灰色系统模型在机床热误差建模中的应用[J]. 中国机械工程, 2006, 17(23): 2439. LI Yongxiang, YANG Jianguo. Application of gray system model to thermal error modeling on machine tools[J]. China Mechanical Engineering, 2006, 17(23): 2439. DOI:10.3321/j.issn:1004-132X.2006.23.005 |
| [5] |
刘志峰, 潘明辉, 张爱平, 等. 基于灰色线性回归组合模型的机床热误差建模方法[J]. 高技术通讯, 2013, 23(6): 631. LIU Zhifeng, PAN Minghui, ZHANG Aiping, et al. Thermal error modeling based on the grey-linear regression combination model for machine tools[J]. High Technology Letters, 2013, 23(6): 631. DOI:10.3772/j.issn.1002-0470.2013.06.013 |
| [6] |
林伟青, 傅建中, 陈子辰, 等. 数控机床热误差的动态自适应加权最小二乘支持矢量机建模方法[J]. 机械工程学报, 2009, 45(3): 178. LIN Weiqing, FU Jianzhong, CHEN Zichen, et al. Modeling of NC machine tool thermal error based on adaptive best-fitting WLS-SVM[J]. Journal of Mechanical Engineering, 2009, 45(3): 178. DOI:10.3901/JME.2009.03.178 |
| [7] |
姜辉, 杨建国, 姚晓栋, 等. 数控机床主轴热漂移误差基于贝叶斯推断的最小二乘支持向量机建模[J]. 机械工程学报, 2013, 49(15): 115. JIANG Hui, YANG Jianguo, YAO Xiaodong, et al. Modeling of CNC machine tool spindle thermal distortion with LS-SVM based on bayesian inference[J]. Journal of Mechanical Engineering, 2013, 49(15): 115. DOI:10.3901/JME.2013.15.115 |
| [8] |
HUANG Yanqun, ZHANG Jie, LI Xu, et al. Thermal error modeling by integrating GA and BP algorithms for the High-speed spindle[J]. International Journal Advance Manufacture Technology, 2014, 71(9/12): 1669. DOI:10.1007/s00170-014-5606-0 |
| [9] |
王续林, 顾群英, 杨昌祥, 等. 基于PSO聚类和ELM神经网络机床主轴热误差建模[J]. 组合机床与自动化加工技术, 2015(7): 69. WANG Xulin, GU Qunying, YANG Changxiang, et al. Modeling for machine tool thermal error based on PSO clustering algorithm and ELM model preprocessing neural network[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(7): 69. DOI:10.13462/j.cnki.Mmtamt.2015.07.019 |
| [10] |
ZHANG Yi, YANG Jianguo, JIANG Hui. Machine tool thermal error modeling and prediction by grey neural network[J]. The International Journal of Advanced Manufacturing Technology, 2012, 59(9-12): 1065. DOI:10.1007/s00170-011-3564-3 |
| [11] |
谭峰, 殷国富, 殷勤, 等. 基于GM-LS-SVM层级模型的数控机床热误差建模[J]. 中南大学学报(自然科学版), 2016, 47(12): 4028. TAN Feng, YIN Guofu, YIN Qing, et al. CNC machine tool thermal error modeling based on GM-LS-SVM hierarchical model[J]. Journal of Zhongnan University, 2016, 47(12): 4028. DOI:10.11817/j.issn.16727207.2016.12.010 |
| [12] |
阳红, 向胜华, 刘立新, 等. 基于最优权系数组合建模的数控机床热误差在线补偿[J]. 农业机械学报, 2012, 43(5): 216. YANG Hong, XIANG Shenghua, LIU Lixin, et al. Online compensation for CNC machine thermal error based on optimal weights-based combined modeling[J]. Transaction of the Chinese Society for Agricultural Machinery, 2012, 43(5): 216. DOI:10.6041/j.issn.10001298.2012.05.037 |
| [13] |
YANG Hong, NI Jun. Dynamic modeling for machine tool thermal error compensation[J]. Journal of Manufacturing Science & Engineering, 2003, 125(2): 245. DOI:10.1115/1.1557296 |
| [14] |
姚焕新, 牛鹏程, 龚亚运, 等. 数控机床热误差补偿中分布滞后模型的建立[J]. 农业机械学报, 2013, 44(3): 246. YAO Huanxin, NIU Pengcheng, GONG Yayun, et al. Establishment of autoregressive distributed lag model in thermal error compensation of CNC machine tools[J]. Transaction of the Chinese Society for Agricultural Machinery, 2013, 44(3): 246. |
| [15] |
苗恩铭, 刘义, 董云飞, 等. 数控机床热误差时间序列模型预测稳健性的提升[J]. 光学精密工程, 2016, 24(10): 2480. MIAO Enming, LIU Yi, DONG Yunfei, et al. Improvement of forcasting robustness of time series model for thermal error on CNC machine tool[J]. Optics and Precision Enginerring, 2016, 24(10): 2480. DOI:10.3788/ope.20162410.2480 |
| [16] |
VAPNIK V. The nature of statistical learning theory[C]// Conference on Artificial Intelligence. Springer-Verlag, 1995: 988
|
| [17] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293. DOI:10.1023/A:1018628609742 |
 2019, Vol. 51
2019, Vol. 51


