2. 金属矿山高效开采与安全教育部重点实验室(北京科技大学), 北京 100083;
3. 中国矿业大学(北京) 资源与安全工程学院, 北京 100083
2. Key Laboratory of High-Efficient Mining and Safety of Metal Mines (University of Science and Technology Beijing), Ministry of Education, Beijing 100083, China;
3. College of Resources & Safety Engineering, China University of Mining & Technology (Beijing), Beijing 100083, China
岩体在地壳中经历了长时间的各种地质作用,通常, 其被各种不同方向的结构面(节理、断层等)交错切割,从而形成复杂的不连续结构状态.故可将节理岩体等效为完整岩石与软弱结构面的组合体,这样其力学行为、破坏机理及损伤演化规律将会更加复杂.通常节理以不同角度及方向分布于岩体空间,因而岩体裂化机制将不可避免地受到节理倾角的影响[1-3],宏观上表现为岩体力学特征及破坏模式的大不相同,细观上表现为损伤演化规律存在巨大差异.
针对节理倾角对岩体力学性质及损伤演化规律的影响,国内外学者[4-6]通过开展力学试验和数值建模方法对其进行了验证分析.孙旭曙等[7-8]对标准岩石试件按不同角度进行切割、粘合得到不同倾角节理岩体试件,然后进行声波测速试验及压缩试验,系统研究了倾角与其物理力学参量之间的内在关系.Yang等[9]研究了节理倾角和间距对砂岩破碎效应的影响,并提出了节理岩石破裂计算模型.Wang等[10]通过对横观各向同性的圆盘试件进行巴西劈裂试验和PFC-2D数值模拟研究,发现其抗拉强度和空间变形存在各向异性特征.Yang等[11]基于室内岩石力学试验,深入分析了节理间距、节理倾角、节理连通率与岩石强度特性和破坏模式之间的内在关系.刘红岩等[12-13]通过开展不同工况预制节理岩体单轴抗压强度试验,重点分析了倾角、贯通率等7种参数对峰值强度及破坏特征的影响,同时建立了节理岩体动态损伤本构模型.王培涛等[14]基于MATLAB及PFC软件,构建了粗糙离散节理模型,同时开展单轴压缩试验,对其力学特性及破坏模式进行了研究.李列列等[15]借助修正自洽方法,基于能量原理,建立了非贯通节理岩体复合损伤本构模型.
无论采用能量理论或应变等价理论进行节理岩体损伤演化特征分析,通常认为节理岩体损伤初始值为0,但是相比完整岩体,节理岩体可认为其存在天然损伤即初始损伤,因此,在进行损伤演化规律研究时要加以考虑,且倾角对其影响很大.若忽略初始损伤的影响,所构建的损伤演化模型难免存在不足之处.因此,借鉴其他学者的研究成果并针对其不足之处[16-19],重点考虑节理倾角对岩体初始损伤的影响,运用连续损伤理论,建立了初始节理损伤与荷载损伤共同作用下的节理岩体损伤本构模型.最后借助孙旭曙等[7-8]的试验结果,对不同角度节理岩体的损伤演化特性进行了深入分析.
1 荷载作用下节理岩体破坏规律分析在荷载作用下,岩体试件逐渐被压缩,首先,结构面开始闭合,岩体试件应变快速增加.当结构面完全闭合继续施加荷载,若岩体试件节理倾角(结构面与水平方向夹角)大于内摩擦角,由摩尔库伦定律可知,此时结构面上的剪切力大于摩擦力,岩体试件强度降低;若节理倾角小于岩体试件内摩擦角,此时结构面上的摩擦力大于剪切力,岩体试件将沿内摩擦角方向发生剪切破坏,试件强度有所增加;若节理倾角接近垂直(90°),在试件端部,由于加载板与试件之间的摩擦效应抑制试件沿节理面发生滑动,此时岩体试件将发生垂直加载方向的张拉破坏,试件强度有一定提高;若节理倾角接近水平(0°),在压缩荷载作用下,试件不发生沿结构面的滑动破坏,但由于结构面上下面之间出现应力集中现象,此时试件将发生张拉破坏,试件强度有所提高.通过对节理岩体破坏规律进行分析,也解释了当节理倾角从0°增加到90°过程中,试件压缩强度出现先减小后增大的“U型”分布的原因.
2 节理岩体损伤演化规律当岩体存在节理时,节理面的存在改变了岩体宏观结构特征,进而导致岩体力学性质发生不可逆劣化,如强度特性减弱、弹性模量降低等,此时认为岩体存在一个初始损伤,可定义此损伤为
| $ {D_\varphi } = 1 - \frac{{{E_\varphi }}}{{{E_0}}}. $ | (1) |
式中:Eφ为节理岩体弹性模量,E0为完整岩体弹性模量,φ为节理倾角(结构面与水平面的夹角).
在外载作用下,岩体内部开始产生各种随机分布的细观损伤,进而可从统计学角度去研究其受荷损伤.借助岩体应变等效假定,结合Weibull分布损伤模型,认为岩体微元强度概率密度函数为[20]
| $ P(\varepsilon ) = \frac{m}{{{\varepsilon _0}}}{\left( {\frac{{\cal E}}{{{\varepsilon _0}}}} \right)^{m - 1}}{{\rm{e}}^{ - {{\left( {\frac{\varepsilon }{{{\varepsilon _0}}}} \right)}^m}}}. $ | (2) |
式中:ε为岩体材料的应变量,m、ε0为分布参数.
当岩体被加载到应变水平ε时,其受荷损伤变量可表示为
| $ {D_{\rm{s}}} = 1 - {{\rm{e}}^{ - {{\left( {\frac{\varepsilon }{{{\varepsilon _0}}}} \right)}^m}}}. $ | (3) |
根据Lemaitre应变等价原理[21],得到此时完整岩体受荷损伤本构关系:
| $ {\sigma _1} = \left( {1 - {D_{\rm{s}}}} \right){E_0}{\varepsilon _1} + 2{\mu _0}{\sigma _3}. $ | (4) |
式中:Ds为岩体受荷损伤变量,μ0为完整岩体泊松比.
节理岩体由于存在初始损伤,当其受到荷载作用时,其损伤本构关系应表示为[22]
| $ {\sigma _1} = \left( {1 - {D_{\rm{s}}}} \right){E_\varphi }{\varepsilon _1} + 2{\mu _\varphi }{\sigma _3}. $ | (5) |
式中μφ为节理岩体泊松比(其中节理倾角为φ).
联立式(1)和(5)即可求得两种损伤耦合状态下的节理岩体本构关系式
| $ {\sigma _1} = \left( {1 - {D_{\rm{s}}}} \right)\left( {1 - {D_\varphi }} \right){E_0}{\varepsilon _1} + 2{\mu _\varphi }{\sigma _3}. $ | (6) |
将式(6)展开可得节理岩体总损伤变量表达式
| $ D = {D_\varphi } + {D_{\rm{s}}} - {D_\varphi }{D_{\rm{s}}}, $ | (7) |
式中D为初始节理损伤与荷载损伤耦合损伤变量.
将式(1)和(3)代入式(7)得
| $ D = 1 - \frac{{{E_\varphi }}}{{{E_0}}}\exp \left[ { - {{\left( {\frac{{\cal E}}{{{\varepsilon _0}}}} \right)}^m}} \right]. $ | (8) |
式(8)即为节理岩体在荷载作用下的总损伤演化方程.分析式(8),对于不含结构面的完整岩石试件,当荷载作用于试件时,Eφ=E0,得到D=Ds;而对于处于初始状态的含结构面的岩体试件,此时ε=0,从而D=Dφ.若同时考虑结构面与荷载共同作用,对式(8)求导即可得到耦合损伤变量演化率方程
| $ {D^\prime } = \left( {1 - {D_\varphi }} \right)\frac{{\partial D}}{{\partial \varepsilon }} + \left( {1 - {D_{\rm{s}}}} \right)\frac{{\partial D}}{{\partial \varphi }}. $ | (9) |
式中D′为节理岩体在荷载作用下的总损伤演化率.
3 节理岩体损伤本构模型根据前文建立的节理岩体损伤演化方程,将其代入岩体损伤本构关系式,即可得到节理岩体受荷损伤本构模型.基于此,联立式(6)和(7)即可得到压缩条件下节理岩体损伤本构的基本关系式为
| $ {\sigma _1} = {E_0}(1 - D){\varepsilon _1} + 2{\mu _\varphi }{\sigma _3}. $ | (10) |
假定试件服从岩石应变强度理论[14],将式(8)代入式(10),得到节理岩体受荷损伤本构模型为
| $ {\sigma _1} = {E_\varphi }{\varepsilon _1}\exp \left[ { - {{\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _0}}}} \right)}^m}} \right] + 2{\mu _\varphi }{\sigma _3}. $ | (11) |
节理岩体试件在荷载作用下的全应力-应变曲线在峰值应力处满足如下两个几何条件:
a) ε1=εf时,σ1=σf;
b) ε1=εf时,
式中:σf和εf为节理岩体试件全应力-应变曲线在峰值应力处的应力和应变值.
将式(11)两边对ε1求偏导,得
| $ \frac{{\partial {\sigma _1}}}{{\partial {\varepsilon _1}}} = {E_\varphi }\exp \left[ { - {{\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _0}}}} \right)}^m}} \right]\left[ {1 - m{{\left( {\frac{{{\varepsilon _1}}}{{{\varepsilon _0}}}} \right)}^m}} \right]. $ | (12) |
将几何条件a)代入式(11)得
| $ {\sigma _f} = {E_\varphi }{\varepsilon _f}\exp \left[ { - {{\left( {\frac{{{\varepsilon _f}}}{{{\varepsilon _0}}}} \right)}^m}} \right] + 2{\mu _\varphi }{\sigma _3}. $ | (13) |
将几何条件b)代入式(12)得
| $ {\left( {\frac{{{\varepsilon _f}}}{{{\varepsilon _0}}}} \right)^m} = \frac{1}{m}. $ | (14) |
联立式(13)和(14)得
| $ m = \frac{1}{{\ln \frac{{{E_\varphi }{\varepsilon _f}}}{{{\sigma _f} - 2{\mu _\varphi }{\sigma _3}}}}}. $ | (15) |
| $ {\varepsilon _0} = {\varepsilon _f}{m^{1/m}}. $ | (16) |
将式(15)和(16)分别代入式(8)和(11),即可得到节理岩体损伤演化模型及损伤本构模型.
4 计算实例及损伤演化特征分析 4.1 计算实例利用孙旭曙等[7-8]的研究成果,按不同倾角(0°,30°,45°,60°和90°,见图 1)将完整的标准岩石试件(φ=50 mm、h=100 mm)切割成两部分,然后利用石膏与水(石膏与水质量比为2:1)的混合溶剂作为胶结剂将两部分切割开的岩石粘合上,以此制作不同倾角节理岩体试件.然后进行压缩试验,获取节理岩体试件物理力学参数,见表 1.
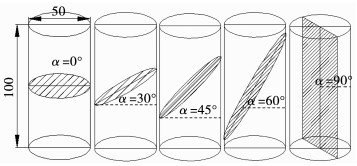
|
图 1 节理岩体标准圆柱体试件 Fig. 1 Standard cylinder specimens of jointed rock mass |
为验证模型试验的合理性,引入岩体强度单结构面强度理论[23].岩体单结构面强度理论认为,当结构面倾角α满足α<α1或α>α2时,岩体强度等于岩石强度,当结构面倾角α满足α1<α<α2时,岩体强度计算公式为
| $ {\sigma _{1, m}} = {\sigma _3} + \frac{{2\left( {{c_{\rm{w}}} + {\sigma _3}{f_{\rm{w}}}} \right)}}{{\left( {1 - {f_{\rm{w}}}\cot \alpha } \right)\sin 2\alpha }}, $ | (17) |
| $ {\alpha _1} = \frac{{{\phi _w}}}{2} + \frac{1}{2}\arcsin \left[ {\frac{{\left( {{\sigma _1} + {\sigma _3} + 2{c_{\rm{w}}}\cot {\phi _{\rm{w}}}} \right)\sin {\phi _{\rm{w}}}}}{{{\sigma _1} - {\sigma _3}}}} \right], $ | (18) |
| $ \begin{array}{l} {\alpha _2} = \frac{{\rm{ \mathit{ π} }}}{2} + \frac{{{\phi _{\rm{w}}}}}{2} - \\ \;\;\;\;\frac{1}{2}\arcsin \left[ {\frac{{\left( {{\sigma _1} + {\sigma _3} + 2{c_{\rm{w}}}\cot {\phi _{\rm{w}}}} \right)\sin {\phi _{\rm{w}}}}}{{{\sigma _1} - {\sigma _3}}}} \right]. \end{array} $ | (19) |
式中:σ1, m为岩体理论抗压强度,cw为结构面内聚力,fw为结构面内摩擦系数,ϕw为结构面内摩擦角.
由文献[24]的研究可知,cw=0.1 MPa,ϕw=23°.结合试验数据及上述cw、ϕw的值,代入式(18)和(19)得到α1和α2的值,见表 2.
| 表 2 不同围压下α1及α2的值 Tab. 2 Values of α1 and α2 under different confining pressures |
根据式(17)即可计算得到含不同倾角单一结构面岩体理论强度,与模型试验强度进行对比分析,结果见图 2.
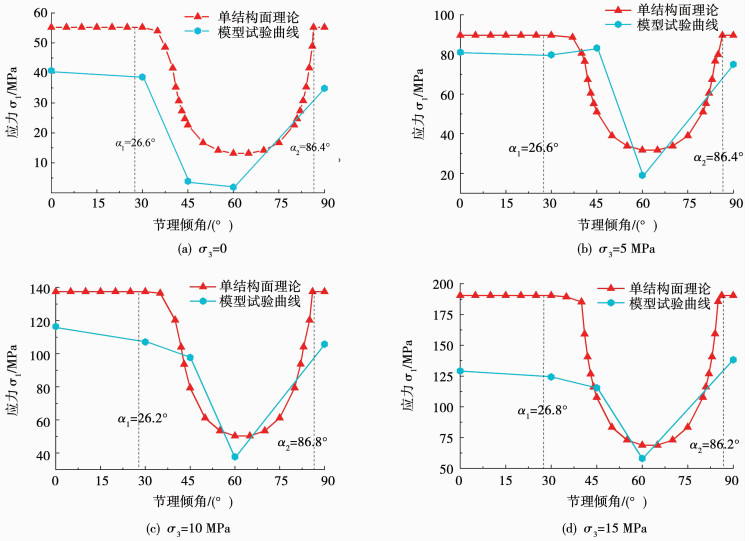
|
图 2 岩体单结构面理论强度与实测强度对比 Fig. 2 Comparison of single structural plane theoretical strength and measured strength of rock mass |
由图 2不同围压下含单结构面岩体强度随结构面倾角变化曲线可以看出:对于模型试验曲线,当结构面倾角从0°增大到30°过程中,模型试验测得的节理岩体强度基本保持不变,当结构面倾角从30°增大到60°过程中,模型实测强度开始急剧减小达到最小值,继续增大结构面倾角至90°时,模型实测强度开始增大,总体呈“U”型分布规律;对于单结构面理论强度曲线,当结构面倾角从0°增大到α1≈26°过程中,岩体强度均为岩石强度,强度基本保持不变,当结构面倾角从30°增大到π/4+φw/2≈56.5°过程中,理论强度急剧减小至最小值,继续增大结构面倾角至α2≈86°过程中,理论强度开始增大,而当结构面倾角从α2≈86°持续增大至90°过程中,岩体强度又与岩石强度一致,总体上也呈现出“U”型分布规律.对比试验强度曲线和理论强度曲线可知,两曲线发展规律非常一致,且重合度较高,随结构面倾角从0°增大到90°过程中,两曲线均表现出如下发展规律:先基本保持不变,然后急剧减小至最小值,而后开始快速增加,最后又基本保持不变.
通过上述分析可知,模型实测曲线与单结构面理论强度曲线发展趋势非常一致,而且数值大小也比较吻合,当围压为0,5和10 MPa时,两条曲线吻合程度非常高,当围压为15 MPa时吻合程度稍差,但总体而言吻合程度较高,因此,可认为本文模型能较好地模拟单结构面岩体,该模型具有一定的合理性.
4.3 节理岩体损伤演化特征分析将表 1中力学参数分别代入式(15)和(16),得到节理岩体损伤本构模型参数m和ε0,结果见表 3.
| 表 3 模型参数m及ε0 Tab. 3 Model parameters m and ε0 |
将表 1中的力学参数代入式(1),可获得初始节理损伤随结构面倾角的变化规律,见图 3.可以看出,节理岩体存在一个初始损伤,且初始损伤值随节理倾角变化而变化,初始损伤与节理倾角直接相关.从图 3曲线变化趋势可知,节理岩体初始损伤随节理倾角增加呈现“U”型分布规律.当结构面倾角从0°增加到90°时,初始损伤先缓慢增加,再快速增加至最大值,最后急剧减小,且当节理倾角为60°时达到最大值,其中初始损伤最大值与最小值比率约为2.13,表明结构面倾角对初始损伤有较大的影响.
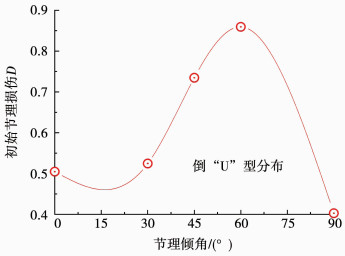
|
图 3 初始节理损伤与节理倾角关系曲线 Fig. 3 Relationship between initial jointed damage and joint dip angle |
将表 1中岩体参数代入式(8),可以计算得到4种不同围压下节理岩体在结构效应与荷载耦合作用下的损伤模型理论曲线,结果见图 4.可以看出,完整岩体试件在荷载作用下损伤从0开始缓慢增加,随着荷载继续增大,试件轴向应变不断累积,损伤进入快速增长阶段,随后应力达到峰值,试件发生失稳破坏,继续压缩试件,试件进入峰后阶段,损伤继续增加,但增速逐渐变缓,直至试件完全破坏,损伤累计值达到1.对于节理岩体,不同节理倾角试件损伤从不同的初始值开始逐渐演化发育,初始阶段,节理面慢慢被压缩闭合,轴向位移增量较大,损伤缓慢累积,随着荷载继续增大,试件发生沿节理面的滑动破坏和张拉破坏,损伤开始迅速累积至试件发生失稳破坏,继续施加荷载,试件进入峰后阶段,损伤累积速率再次放缓至试件完全破坏,损伤值达到1.
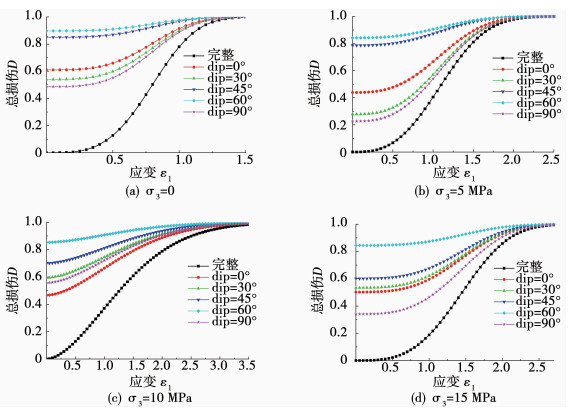
|
图 4 节理岩体受荷损伤演化曲线 Fig. 4 Damage evolution curve of jointed rock mass with load |
对比节理岩体试件与完整试件,其损伤演化规律总体上相似,均为先缓慢增加,然后快速增加至试件达到峰值,最后又缓慢增加至1,试件完全破坏,两者不同之处在于完整试件没有初始损伤,试件损伤从0开始逐渐演化至1,试件完全破坏,而节理岩体试件存在一个初始损伤,在荷载作用下,损伤从不同初始值开始逐渐演化至1,试件完全破坏.
另外,由图 4可直观看出,当结构面倾角为60°时,节理岩体初始损伤值非常大,试件近乎破坏,在此角度下,节理岩体强度特性很差.而当结构面角度为0°和90°时,初始损伤值相对非常小,此角度下节理岩体强度特征有所增加.原因是:当节理倾角为60°时,节理倾角大于试件内摩擦角,对试件进行压缩,此时节理面上的剪切力大于其摩擦力与黏聚力之和,试件将沿节理面发生滑动破坏,抗压强度非常低;当节理倾角为0°或90°时,试件将不再沿节理面发生滑动破坏,抗压强度得到较大提升.试验现象与文章所构建的节理岩体损伤演化模型非常吻合,模型具有一定的合理性.
根据式(9)可以计算得到4种不同围压下节理岩体在结构效应与荷载耦合作用下的总损伤率演化曲线,结果见图 5.可以看出,不同倾角下节理岩体总损伤率演化规律基本一致,倾角不同,总损伤率大小略有差异.当围压恒定,总损伤率随应变增加从0开始缓慢增加,然后快速增加至峰值后又急剧减小,最后再次慢慢减小为0,总损伤率演化曲线近乎呈正态分布.
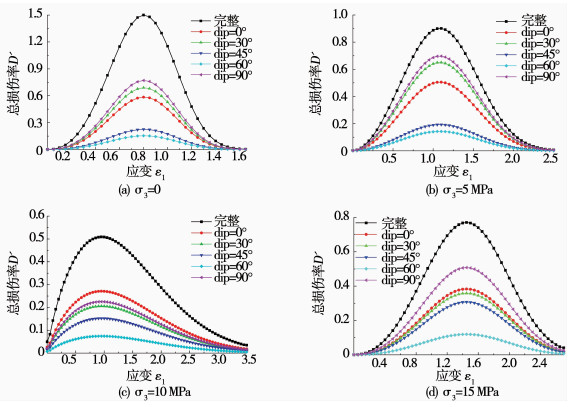
|
图 5 节理岩体总损伤率演化曲线 Fig. 5 Total damage evolution curve of jointed rock mass |
取图 5中相同应变下的节理岩体总损伤率,可得到节理岩体总损伤率随节理倾角的变化规律,结果见图 6.图 6直观地反映了节理岩体损伤演化率受控于节理面空间分布规律.总体而言,总损伤演化率随节理倾角增大先减小后增加.以围压σ3=10 MPa、应变ε1=0.007为例进行说明,当节理面水平分布时,其总损伤率为0.257,当节理面与水平面夹角为30°时,总损伤率减小至0.195,减小约24.1%,当夹角进一步扩大到45°时,总损伤率为0.144,降幅达44.0%,而当夹角增至60°时,总损伤率降至最小0.071,下降幅度最大为72.4%,而继续增大夹角至90°时,总损伤率开始增加为0.214,约为夹角60°时的3倍.
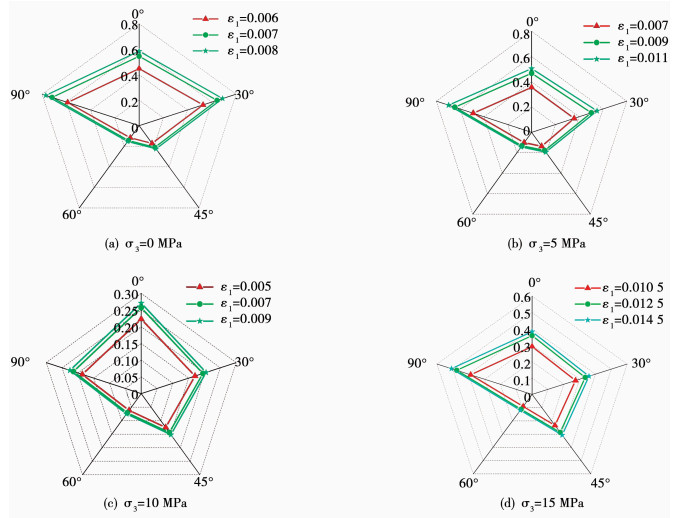
|
图 6 节理岩体总损伤率与节理倾角关系曲线 Fig. 6 Relationship between total damage rate and joint dip angle |
通过对节理岩体总损伤演化规律及总损伤率演化规律的深入分析,可知文中构建的节理岩体损伤演化模型与文献[7-8]的研究结论基本一致,认为文中的损伤演化模型具有一定适用性,可为节理岩体损伤规律研究提供一定的参考价值.
5 结论1) 节理岩体总损伤包括初始节理损伤和荷载损伤;建立了初始损伤与荷载损伤共同作用下的节理岩体损伤演化模型及损伤本构模型;借助单弱面理论对模型试验的合理性进行了验证,模型试验能较好地表征含单结构面的岩体在荷载作用下的力学特征及损伤演化规律.
2) 初始节理损伤随节理倾角从0°增大到90°过程中先增后减,在60°时至最大值,且总体呈现倒“U”型分布规律;节理岩体总损伤演化曲线随应变增大均呈“S”型分布,先缓慢增加,然后快速增加,最后再缓慢增加其值趋于1.
3) 节理倾角只影响节理岩体总损伤率数值大小,不影响其演化规律;总损伤率随应变增加先缓慢增加,然后快速增加至峰值后又急剧减小,最后再次慢慢减小为0,且演化曲线近乎为正态分布.
4) 节理岩体总损伤率受控于节理面空间分布规律,当节理倾角从0增大至90的过程中,总损伤率先减小后增大.
| [1] |
汪杰, 宋卫东, 付建新. 考虑节理倾角的岩体损伤本构模型及强度准则[J]. 岩石力学与工程学报, 2018, 37(10): 2253. WANG Jie, SONG Weidong, FU Jianxin. A damage constitutive model and strength criterion of rock mass considering the dip angle of joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(10): 2253. |
| [2] |
CHIU C C, WENG M C, HUANG T H. Modeling rock joint behavior using a rough-joint model[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 89: 14. DOI:10.1016/j.ijrmms.2016.08.001 |
| [3] |
MENG J, HUANG J, SLOAN S W, et al. Discrete modelling jointed rock slopes using mathematical programming methods[J]. Computers and Geotechnics, 2018, 96: 189. DOI:10.1016/j.compgeo.2017.11.002 |
| [4] |
韩智铭, 乔春生, 朱举. 含两组交叉贯通节理岩体的强度及破坏特征分析[J]. 岩土力学, 2018, 39(7): 1. HAN Zhiming, QIAO Chunsheng, ZHU Ju. Analysis on strength and failure characteristics of rock mass with two sets of cross-persistent joints[J]. Rock and Soil Mechanics, 2018, 39(7): 1. DOI:10.16285/j.rsm.2017.1741 |
| [5] |
李列列, 肖明砾, 卓莉, 等. 考虑非贯通节理损伤演化岩体复合本构模型[J]. 哈尔滨工业大学学报, 2017, 49(6): 96. LI Lielie, XIAO Mingli, ZHUO Li, et al. Compound constitutive model considering damage evolution of non-persistent fractured rock mass[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 96. DOI:10.11918/j.issn.0367-6234.201610052 |
| [6] |
陈新, 孙靖亚, 杨盼, 等. 节理间距和倾角对岩体单轴压缩破碎规律的影响[J]. 采矿与安全工程学报, 2017, 34(3): 608. CHEN Xin, SUN Jingya, YANG Pan, et al. Influence of joint spacing and inclination angle on fragmentation characteristic of rock masses under uniaxial compression[J]. Journal of Mining & Safety Engineering, 2017, 34(3): 608. DOI:10.13545/j.cnki.jmse.2017.03.029 |
| [7] |
孙旭曙, 李建林, 王乐华, 等. 单一预制节理试件各向异性力学特性试验研究[J]. 岩土力学, 2014, 35(增刊1): 29. SUN Xushu, LI Jianlin, WANG Lehua, et al. Experimental research on anisotropic mechanical characteristic of samples with single prefabricated joint[J]. Rock and Soil Mechanics, 2014, 35(Suppl 1): 29. DOI:10.16285/j.rsm.2014.s1.004 |
| [8] |
孙旭曙, 李建林, 王乐华, 等. 节理岩体超声测试及单轴压缩试验研究[J]. 岩土力学, 2014, 35(12): 3473. SUN Xushu, LI Jianlin, WANG Lehua, et al. Study of ultrasonic test and uniaxial compression test of jointed rock masses[J]. Rock and Soil Mechanics, 2014, 35(12): 3473. DOI:10.16285/j.rsm.2014.12.018 |
| [9] |
YANG Haiqing, LIU Junfeng, LIU Bolong. Investigation on the cracking character of jointed rock mass beneath TBM disc cutter[J]. Rock Mechanics and Rock Engineering, 2018, 51: 1263. DOI:10.1007/s00603-017-1395-8 |
| [10] |
WANG Peitao, CAI Meifeng, REN Fenhua. Anisotropy and directionality of tensile behaviours of a jointed rock mass subjected to numerical Brazilian tests[J]. Tunnelling and Underground Space Technology, 2018, 73: 139. DOI:10.1016/j.tust.2017.12.018 |
| [11] |
YANG Xuxu, JING Hongwen, TANG Chunan, et al. Effect of parallel joint interaction on mechanical behavior of jointed rock mass models[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 92: 40. DOI:10.1016/j.ijrmms.2016.12.010 |
| [12] |
刘红岩, 黄妤诗, 李楷兵, 等. 预制节理岩体试件强度及破坏模式的试验研究[J]. 岩土力学, 2013, 34(5): 1235. LIU Hongyan, HUANG Yushi, LI Kaibing, et al. Test study of strength and failure mode of pre-existing jointed rock mass[J]. Rock and Soil Mechanics, 2013, 34(5): 1235. DOI:10.16285/j.rsm.2013.05.002 |
| [13] |
刘红岩, 吕淑然, 张力民. 基于组合模型法的贯通节理岩体动态损伤本构模型[J]. 岩土工程学报, 2014, 36(10): 1814. LIU Hongyan, LV Shuran, ZHANG Limin. Dynamic damage constitutive model for persistent jointed rock mass based on combination model method[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(10): 1814. DOI:10.11779/CJGE201410008 |
| [14] |
王培涛, 任奋华, 谭文辉, 等. 单轴压缩试验下粗糙离散节理网络模型构建及力学特性[J]. 岩土力学, 2017, 38(增刊1): 70. WANG Peitao, REN Fenhua, TAN Wenhui, et al. Model of roughness discrete fractures network for uniaxial compressive test and its mechanical properties[J]. Rock and Soil Mechanics, 2017, 38(Suppl 1): 70. |
| [15] |
李列列, 肖明砾, 卓莉, 等. 考虑非贯通节理损伤演化岩体复合本构模型[J]. 哈尔滨工业大学学报, 2017, 49(6): 96. LI Lielie, XIAO Mingli, ZHUO Li, et al. Compound constitutive model considering damage evolution of non-persistent fractured rock mass[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 96. DOI:10.11918/j.issn.0367-6234.201610052 |
| [16] |
涂洪亮, 乔春生, 朱举. 节理岩体抗力系数的各向异性特征与计算方法[J]. 哈尔滨工业大学学报, 2019, 51(2): 90. TU Hongliang, QIAO Chunsheng, ZHU Ju. Anisotropic characteristic and calculation of the resistant coefficient of the jointed rock mass[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 90. DOI:10.11918/j.issn.0367-6234.201712022 |
| [17] |
陈松, 乔春生, 叶青, 等. 冻融荷载下节理岩体的复合损伤模型[J]. 哈尔滨工业大学学报, 2019, 51(2): 100. CHEN Song, QIAO Chunsheng, YE Qing, et al. Composite damage model of jointed rock mass under freezing and thawing load[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 100. DOI:10.11918/j.issn.0367-6234.201711056 |
| [18] |
ZHANG Zhenghu, DENG Jianhui, ZHU Jianbo, et al. An experimental investigation of the failure mechanisms of jointed and intact marble under compression based on quantitative analysis of acoustic emission waveforms[J]. Rock Mechanics and Rock Engineering, 2018, 51(7): 2299. DOI:10.1007/s00603-018-1484-3 |
| [19] |
SINGH M, RAO K S, RAMAMURTHY T. Strength and deformational behaviour of a jointed rock mass[J]. Rock Mechanics and Rock Engineering, 2002, 35(1): 45. DOI:10.1007/s006030200008 |
| [20] |
张慧梅, 彭川, 杨更社, 等. 考虑冻融效应的岩石损伤统计强度准则研究[J]. 中国矿业大学学报, 2017, 46(5): 1066. ZHANG Huimei, PENG Chuan, YANG Gengshe, et al. Study of damage statistical strength criterion of rock considering the effect of freezing and thawing[J]. Journal of China University of Mining & Technology, 2017, 46(5): 1066. |
| [21] |
张慧梅, 杨更社. 冻融与荷载耦合作用下岩石损伤模型的研究[J]. 岩石力学与工程学报, 2010, 29(3): 471. ZHANG Huimei, YANG Gengshe. Research on damage model of rock under coupling action of freeze-thaw and load[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 471. |
| [22] |
张慧梅, 杨更社. 冻融荷载耦合作用下岩石损伤力学特性[J]. 工程力学, 2011, 28(5): 161. ZHANG Huimei, YANG Gengshe. Damage mechanical characteristics of rock under freeze-thaw and load coupling[J]. Engineering Mechanics, 2011, 28(5): 161. |
| [23] |
蔡美峰, 何满朝, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2002: 104. CAI Meifeng, HE Manchao, LIU Dongyan. Rock mechanics and engineering[M]. Beijing: Science Press, 2002: 104. |
| [24] |
孙旭曙.节理岩体卸荷各向异性力学特性试验研究及工程应用[D].武汉: 武汉大学, 2013 SUN Xushu. Experimental research and its engineering application of anisotropic mechanics characteristic in jointed rock mass under unloading condition[D]. Wuhan: Wuhan University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10486-1013209636.htm |
 2019, Vol. 51
2019, Vol. 51


