中国的高速铁路快速发展,运营里程不断增加,至今已超过2万公里,到2025年,高速铁路将达到3.8万公里,覆盖大多数大城市.而高速铁路的防震减灾问题一直受到重视.高速铁路的防震减灾涉及到两个层次的问题:一是首先保证基础设施满足抗震设防的要求,目前已有较成熟的设计标准;二是在基础设施安全的条件下地震时列车的运行安全,目前尚无成熟的解决方案.
在过去的地震中,曾发生多起列车脱轨和颠覆事故.1976年唐山地震中,位于京山线震区的运行列车有货车28列,客车7列,其中,客车两列、货车5列发生部分车辆脱轨或倾覆[1].1995年日本阪神地震中,共有16列列车受损,85辆车脱轨,轨道严重变形[2].2004年日本新潟地震中,新干线列车“朱鹮325”号第8节车厢在时速200 km/h下脱轨,其中由10节车厢组成的列车中有7节车厢脱轨.
因此为解决地震对高速铁路运行安全的威胁,除了进行高速铁路结构的抗震设计外,日本等国家采取了地震预警的方法,当预测的地震动达到一定阈值时,对高速列车进行减速或停车控制,从而减小列车脱轨的危险,减轻地震损失.中国部分高速铁路在建设过程中,已经预先设置了地震监测系统,以备地震预警使用,但在地震预警方面的研究刚刚起步,可参照的经验较少,相关参数如预警阈值等的合理性有待进一步研究和验证.
高速铁路地震预警系统主要包括3个方面的问题:第一是预测预警目的地的地震动强度,主要涉及利用早期监测到的较小的先达地震动预测预警目的地后续破坏性地震动的大小;第二是确定地震作用时目的地的地震动预警阈值,与地震作用下列车的运行安全性密切相关;第三是预警信息的传输、发布和控制方法,主要包括传输发布的技术途径和控制策略和控制方式.本文主要探讨第二个问题,即预警阈值的确定.
高速铁路地震预警阈值涉及地震中列车运行的安全标准.日本是地震预警发展最早的国家,在20世纪60年代就考虑了铁路地震预警系统,其中新干线设置的预警阈值为40 gal[3].中国学者本世纪初开始对铁路地震预警问题进行研究,文献[4]针对京沪高速铁路,以最大轨道允许横向加速度为基准,选取了60条具有代表性的地震波,通过对京沪高速铁路各类典型的构筑物的大量的地震响应统计分析,得到各类构筑物的动力响应系数95%概率上位值约为2.55,然后以轨道横向加速度限值(120 gal)除以动力相应系数得到预警阈值为45 gal.文献[5]利用SI指标选取了4条典型的水平地震波分析了桥上列车地震预警阈值,并建议阈值设为40 gal.
高速铁路的地震预警阈值与地震作用下列车的动态响应、轮重减载和脱轨密切相关,文献[6-9]分析了车辆轨道的动态响应,包括车轮抬升和横移.以30 mm车轮抬升量作为极限,得出了不同地震波频率所应对的,车辆安全运行的临界幅值曲线,同时,通过模拟车辆轨道全尺寸振动台试验,验证了数值分析结果,并建议车辆运行的临界幅值曲线可以应用于车辆轨道结构设计.文献[10]对地震情况下高速列车的动力响应进行了分析,提出了两种新型的高速列车脱轨评价准则,即轮轨接触点位置和车轮抬升量.文献[11-13]认为地震激励频率较低时,易发生倾覆脱轨,地震激励频率较高时,易发生跳轨脱轨.文献[14-15]认为低频地震波对车辆的安全影响较大,当地震波频率在0.5~1 Hz之间,容易与车体发生共振,从而影响车辆行车安全.文献[16-19]对地震激励下列车运行情况进行了仿真模拟,然后利用滚动振动台建立了1: 10的小型模型来进行模拟试验,最后通过车辆轨道全尺寸滚动振动台试验,验证了仿真模拟结果和车辆轨道1: 10缩尺试验结果的正确性,从而证明,在地震作用下对列车脱轨起主导作用的是车体的侧滚运动以及轮轨蠕滑作用下的车轮横移,且脱轨的原因与地震激励的振幅有关,与车速无关.
总体看来,对地震作用下车辆轨道的动态响应、脱轨机理以及地震波幅频特性对车辆轨道运行安全的影响,已经有较一致的认识.这对于确定地震预警的阈值有一定参考价值.本文利用车辆-轨道模型振动台试验的试验结果来验证数值计算模型的准确性,提出一个确定地震预警阈值的初步思路,并根据典型地震波作用下的车辆轨道响应特性,给出地震预警阈值的建议值.
1 车辆-轨道系统振动台模型试验 1.1 试验设备试验在中国建筑科学研究院抗震实验室进行.试验模型各部件从上往下依次为车体、转向架、钢轨、扣件、轨道板、振动台.振动台模型如图 1(a)所示.车厢采用角型钢和钢板围焊而成,车体底座采用框格箱体结构,框格由横向与纵向的矩形钢管拼焊而成,车体与转向架之间通过两侧旁撑支撑和心盘支撑进行连接,且旁撑支撑、心盘支撑为板材焊接式结构,车体自重2 t.轨道板为中国自主研发的CRTSⅢ型轨道板,质量为6.3 t,如图 1(b)所示,转向架采用石家庄车辆厂国产K2型转向架,质量为4.1 t,如图 1(c)所示,钢轨为60 kg/m轨,扣件采用WJ-8b型扣件,如图 1(d)所示,为了较好地模拟半车体质量,采用添加配重块的方法进行车体质量模拟,如图 1(e)所示,配重约为14 t.对轨道板板面进行钻孔设计,采用14根直径为30 mm的钢螺栓将轨道板锚固在振动台中央,使车辆-轨道模型可以随振动台同步振动,见图 1(a).车辆轨道模型其他尺寸参数:轨道板长为4 980 mm,宽为2 500 mm,厚为200 mm;轨距宽为1 435 mm;车体长为2 900 mm,宽为2 400 mm;车体底座高度为250 mm;车轮直径为840 mm.

|
图 1 车辆-轨道模型振动台试验 Fig. 1 Vehicle-track model shaking table test |
考虑到在施加地震荷载的过程中容易发生车体摇摆和倾覆现象,故在试验模型周围架设黄色防倒塌钢架,如图 2所示,确保试验安全进行.同时为防止车辆在振动过程中在轨道上滑动,采用两根直径为5 mm的钢弦将车体中部的前后端拴在防倒塌钢架的前后中柱上.

|
图 2 车辆-轨道振动台试验 Fig. 2 Vehicle-track shaking table test |
试验采用WP-S型位移计(精度0.01 mm)量测车轮抬升量和轮轨水平相对位移,位移计布置见图 3;采用直角应变花,通过组全桥的方式量测轮轨之间的垂向力和水平向力,图 4为应变片组桥示意图,其中图 4(a)中,A1-A8为测试轮轨垂向力的应变片.为方便轮轨力的量测和读取,试验开始前应按照规范TB/T 2489—2016[20]所提方法对轨道的垂向力和水平向力进行标定,标定方法见图 5.采用抗震实验室专用加速度传感器对车辆-轨道模型各部件进行加速度的量测,具体测点布置见图 6.

|
图 3 轮轨垂向、水平向位移计布置 Fig. 3 Layout of vertical and horizontal displacement of wheel-track |

|
图 4 测量轨道力应变片示意图 Fig. 4 Diagram of measuring the track force strain gauge |

|
图 5 轨道水平向力、垂向力标定 Fig. 5 Calibration of the horizontal and vertical force of track |
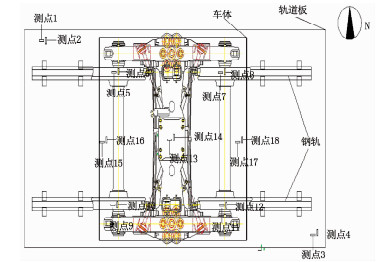
|
图 6 加速度测点布置 Fig. 6 Layout of acceleration measurement point |
对车辆-轨道模型施加的地震波分别为5个周期的正弦地震波、El-centro波、Kobe波和人工波,每条地震波均分级加载,其中地震波输入方向为水平向的共24个工况,输入方向为双向的共1个工况,即水平向、垂向同时施加El-centro地震波,总计25个工况.地震波施加方向分别为Y方向和Z方向,其中Y方向为水平向、Z方向为垂向,试验模型设计简图如图 7所示,限于篇幅原因,只列出部分工况,见表 1.
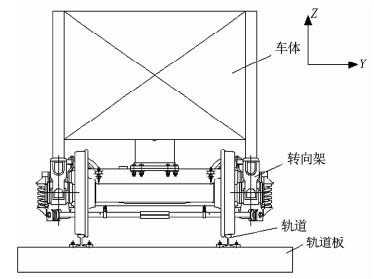
|
图 7 车辆-轨道模型振动台试验设计图 Fig. 7 Vehicle-track model shaking table test design |
| 表 1 部分地震波加载工况表 Tab. 1 Partial seismic wave loading conditions |
模型从上往下分别为车体-转向架-轮对-钢轨-扣件-轨道板.根据车辆-轨道动力学理论,高速列车的单节车辆可简化为由车体、构架、轮对和一、二系弹簧组成,轮对和构架间用一系弹簧连接,而车体与构架则用二系弹簧连接.钢轨与轨道板之间建立了弹簧阻尼单元来模拟扣件.
车辆系统包含1个车体、1个构架、1个轮对共3个刚体结构,各刚体考虑横向、垂向、侧滚这3个方向的自由度,整个车辆系统由9个自由度的多刚体模拟,另外,一、二系弹簧以及扣件系统均采用Pro Cartesian弹簧单元进行模拟,地震荷载从轨道板底部输入,整个计算模型如图 8所示.
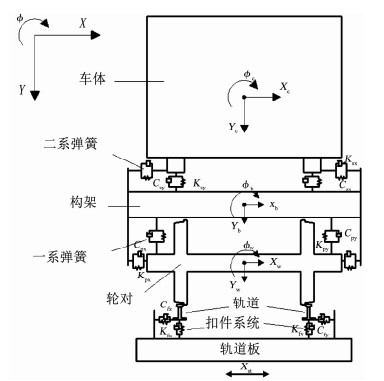
|
图 8 车辆动力学模型 Fig. 8 Vehicle dynamics model |
在动力学模型中,车轮内径为845 mm,外径为915 mm,厚度为145 mm,钢轨采用标准60轨,轨高为176 mm,下宽为150 mm,上宽为73 mm,腰厚为16.5 mm.钢轨间距根据规范取为1 435 mm,车轮之间的轮轴为100 mm.轨道板铺于钢轨之下,长为2.5 m,厚度为260 mm,为混凝土结构.钢轨、轨道板和扣件系统均采用线弹性本构模型,其中钢轨杨氏模量为206 GPa,泊松比为0.3,密度为7 800 kg/m3;轨道板杨氏模量为35.5 GPa,泊松比为0.1,密度为2 400 kg/m3;扣件刚度为78 kN/mm,阻尼系数为50 kN·s/m.
轨道上部结构各部件动力学参数设置分别为车体质量Mc为15 030 kg,其Z轴转动惯量Icz为7.506× 104 kg·m2;转向架质量Mb为3 890 kg,其Z轴转动惯量Ibz为2 260 kg·m2;轮对质量Mw为1 755 kg,其Z轴转动惯量Iwz为915 kg·m2;一系弹簧横向刚度Kpx为12 000 kN/m,其垂向刚度Kpy为1 260 kN/m,其垂向阻尼Cpz为6 kN·s/m;二系弹簧横向刚度Ksx为176 kN/m,其垂向刚度Ksy为235 kN/m,其横向阻尼Csx为1.22 kN·s/m,其垂向阻尼Csy为16. 5 kN·s/m.
2.2 轮轨接触设置模型中采用施加接触对的方式模拟轮轨间的相互作用,轮轨空间动态接触力模型包括轮轨切向力计算模型和轮轨法向力计算模型两部分.轮轨切向力则采用“罚函数”的计算方法,接触面的摩擦系数设为0.3;轮轨法向力表征的是轮轨接触处法向荷载与局部变形之间的关系,采用“Hertz”接触的接触方法对模型进行分析,轮轨接触示意图如图 9所示.
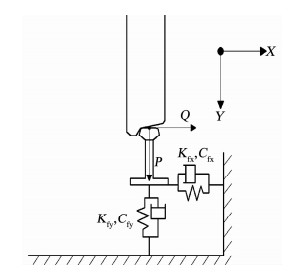
|
图 9 轮轨接触示意图 Fig. 9 Diagram of wheel and rail contact |
Hertz首先用数学弹性力学方法导出接触问题的计算公式.其假设条件:认为材料是均匀的,各向同性的、完全弾性的;接触表面的摩擦力可忽略不计,表面是理想的光滑表面,Hertz接触公式为
| $ N(t)=\left\{\begin{array}{l}{\left[\frac{1}{G_{\mathrm{wr}}} Z_{\mathrm{wrnc} }(t)\right]^{3 / 2}, Z_{\mathrm{wrnc}}(t)>0}; \\ {0, Z_{\mathrm{wrnc}}(t) \leqslant 0}.\end{array}\right. $ | (1) |
式中:Gwr为轮轨接触常数, m/N2/3; Gwr=3.86 R-0.115×10-8;Zwrnc(t)为轮轨接触点的渗透量,其计算公式为
| $ \left\{\begin{array}{l}{\delta Z_{\mathrm{L}}=Z_{\mathrm{w}}(t)-\left(\Delta Z_{\mathrm{Lwt}}-\Delta Z_{\mathrm{w} 0}\right)}, \\ {\delta Z_{\mathrm{R}}=Z_{\mathrm{w}}(t)-\left(\Delta Z_{\mathrm{Rwt}}-\Delta Z_{\mathrm{w} 0}\right)}.\end{array}\right. $ | (2) |
其中:ΔZLwt, ΔZRwt分别为t时刻轮对左右轮轨最小垂向间距;ΔZw0为0时刻左右轮轨最小垂向间距;Zw(t)为t时刻轮对质心的垂向位移.通过轮轨法向压缩量与轮轨之间的几何关系,可以得到左右侧轮轨法向方向的压缩量为
| $ \left\{\begin{aligned} \delta Z_{\mathrm{Lc}} &=\frac{\delta Z_{\mathrm{L}}}{\cos \cos \left(\delta_{\mathrm{L}}+\varphi_{\mathrm{w}}\right)} , \\ \delta Z_{\mathrm{Rc}} &=\frac{\delta Z_{\mathrm{R}}}{\cos \cos \left(\delta_{\mathrm{R}}-\varphi_{\mathrm{w}}\right)}. \end{aligned}\right. $ | (3) |
上述车辆轨道模型参数均与振动台模型试验一致.拟通过和振动台模型试验结果相对比,来验证本文所建立的车辆-轨道计算模型的准确性.
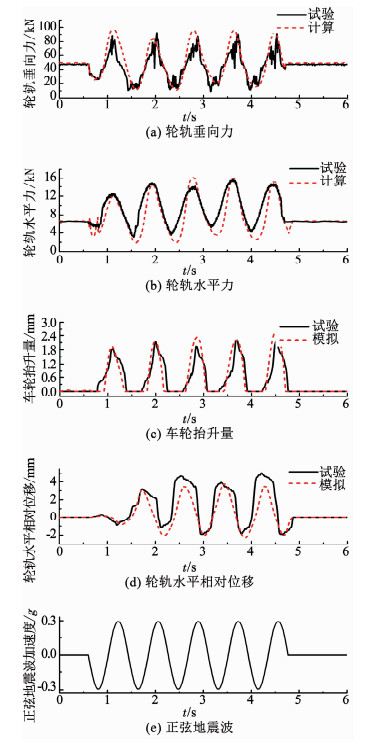
将正弦地震波施加到车辆轨道动力学模型底部,进行地震时程分析,分别绘出轮轨垂向力、轮轨水平力、车轮抬升量、轮轨相对水平位移的动态响应随地震激励时间的变化规律,并与车辆轨道振动台模型试验结果进行对比分析.
通过对比,如图 10所示,发现数值计算结果与振动台模型试验结果基本一致,虽细节处存在一定差异,但从两种结果的周期和峰值来看, 数值计算结果与试验结果相吻合,表明车辆-轨道数值计算模型完美地模拟了试验的真实状态.
|
图 10 数值模拟结果与振动台试验结果对比 Fig. 10 Comparison of numerical simulation results and shaking table test results |
在铁路设计建造和养护维修中常利用脱轨系数、轮重减载率等来评价列车正常运行的安全状态,而养护标准中的脱轨系数等限值与脱轨极限尚有一段差距,例如,脱轨系数养护维修限值为0.8,国际铁路联盟规定脱轨系数限值为Q/P≤1.2[21],由此可以判断出列车正常运行状态下脱轨系数存在相当大的安全冗余量.考虑到地震是概率很小的偶然作用,因此,可以考虑利用列车运行状态之间的安全冗余作为确定地震预警阈值的一个途径,其中地震作用假定可以按列车静止状态考虑.这一途径的优势是对于静止状态的列车-轨道在地震作用下的动态响应, 可以通过振动台试验予以检验;其主要缺陷是实际上,列车运行与地震作用可能产生耦合作用,但文献[16-19]的缩尺滚动台的振动台试验表明,地震作用下的脱轨与列车速度关系不大.因此,可以将上述路径作为确定地震预警阈值的初步近似.
本文拟在数值模拟基础上,提出地震预警阈值的初步建议,主要包括:1)将地震作用下列车运行状态看作为列车在不平顺的轨道上运行和地震作用下列车在光滑的轨道上运行这两种状态的叠加,列车在光滑的直线轨道上运行时的轮轨作用力可近似等效于列车静止状态时的轮轨作用力(不考虑轮轨随机蠕滑力),则采用地震作用下列车静态的方法计算脱轨系数、轮重减载率等脱轨指标.2)中国《高速铁路设计规范(试行)》[22]规定列车的脱轨系数限值为Q/P≤0.8,国际铁路联盟规定脱轨系数限值为Q/P≤1.2,将安全冗余量作为地震作用下列车静止状态时的脱轨系数限值.3)采用典型地震记录,通过数值模拟,确定地震作用下静止状态列车的脱轨系数等参数与地震动峰值加速度之间的关系,从而利用脱轨系数限值确定高速铁路的列车地震预警阈值.
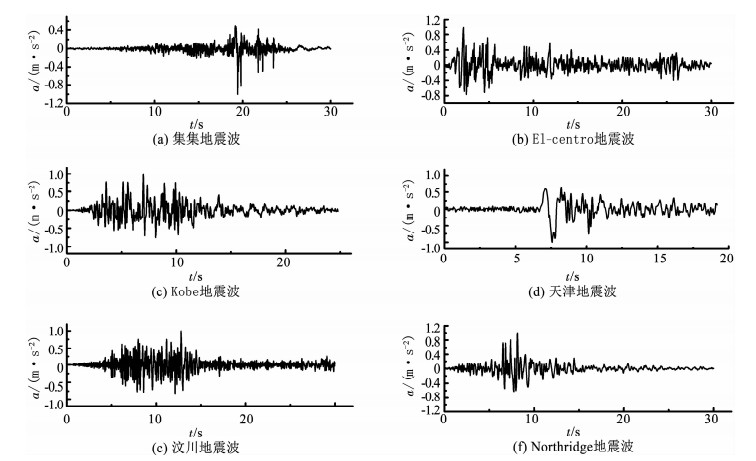
3.2 地震预警阈值的确定为研究列车地震预警阈值,采用本文所述车辆轨道动力学模型,通过6条典型的地震波对车辆-轨道模型进行动力响应分析,6条地震波分别为:台湾集集地震波,持时为30 s,加速度峰值为-357.5 cm/s2;美国加州El-centro地震波,持时为30 s,加速度峰值为334.8 cm/s2;日本Kobe地震波,持时为25 s,加速度峰值为337.9 cm/s2;天津地震波,持时19.19 s,加速度峰值为-104 cm/s2;汶川卧龙地震波,持时30 s,加速度峰值为653 cm/s2;美国Northridge地震波,持时为30 s,加速度峰值为556.9 cm/s2.对6种地震波加速度进行规格化处理,地震波时程曲线如图 11所示.
|
图 11 地震波加速度峰值0.1g时程曲线 Fig. 11 Curves of seismic wave acceleration peak at 0.1g time history |
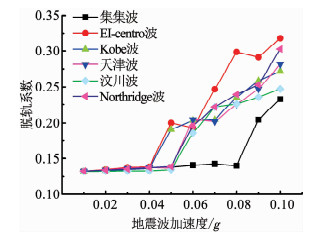
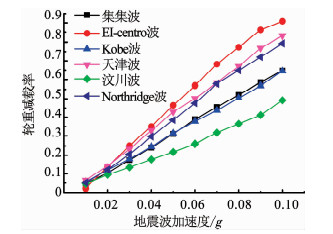
按0.01g的增量分别将各地震波加速度峰值调整为0.01g、0.02g、0.03g、0.04g、0.05g、0.06g、0.07g、0.08g、0.09g、0.1g,图 12为各地震波加速度峰值为0.1g时的加速度时程曲线.依次将上述地震波输入到车辆-轨道模型底部,进行时程分析计算.分别求解计算出模型在各级地震波作用下的脱轨系数和轮重减载率,并以各级地震波加速度峰值为横坐标,各级地震波作用下的脱轨系数和轮重减载率的最大响应值为纵坐标分别绘制曲线,如图 12、13所示.
|
图 12 脱轨系数与地震波峰值加速度关系 Fig. 12 Relationship between derailment coefficient and peak acceleration of seismic wave |
|
图 13 轮重减载率与地震波峰值加速度关系 Fig. 13 Relationship between wheel load reduction rate and peak acceleration of seismic wave |
将集集波、El-centro波、Kobe波、天津波、汶川波、Northridge波依次编号为1#、2#、3#、4#、5#、6#.由图 12可以得到地震作用下列车静止状态时不同脱轨系数限值所对应的各地震波加速度峰值(列车地震预警阈值)关系,见表 2,表中“—”表示该值已超出0.1g.
| 表 2 脱轨系数限值与列车地震预警阈值关系表(hebing) Tab. 2 Relationship between derailment coefficient limit and train earthquake warning threshold |
由表 2可知,当脱轨系数限值为0.1时,预警阈值为0.01g;限值为0.15时,预警阈值为0.04g;限值为0.2时,预警阈值为0.06g;限值为0.25时,预警阈值为0.09g;限值为0.3时,预警阈值为0.1g.
同样由图 13可以得到地震作用下列车静止状态时不同轮重减载率限值所对应的各地震波加速度峰值(列车地震预警阈值)关系表,参见表 3,表中“—”表示该值已超出0.1g.
| 表 3 轮重减载率限值与列车地震预警阈值关系表 Tab. 3 Relationship between wheel load reduction rate limit and train earthquake warning threshold |
由表 3可知,当轮重减载率限值为0.1时,预警阈值为0.02g;限值为0.2时,预警阈值为0.03g;限值为0.3时,预警阈值为0.04g;限值为0.4时,预警阈值为0.05g;限值为0.5时,预警阈值为0.06g.限值为0.6时,预警阈值为0.07g.
综上所述,表 2、3分别给出了不同脱轨系数限值和不同轮重减载率限值相对应的预警阈值,鉴于日本新干线的预警阈值为40 gal,建议中国高速铁路的地震预警阈值也设为40 gal,即可将地震作用下列车静止状态时的脱轨系数限值设为0.15,轮重减载率限值设为0.3.后续工作中,将继续进行全尺寸的车辆-轨道振动台模型试验,继续探索和研究地震作用下列车的脱轨机理和预警阈值.
4 结论1) 对车辆-轨道模型进行全尺寸振动台模型试验,同时建立车辆轨道数值模型,通过采用“Hertz”接触计算方法对数值模型进行计算,并将数值模拟结果与振动台试验结果进行对比分析,发现数值计算结果与振动台模型试验结果虽在细节处存在一定差异,但从两种结果的周期和峰值来看数值计算结果与试验结果相吻合,因此验证了车辆-轨道数值模型的正确性.
2) 提出了确定高速铁路地震预警阈值的新思路,将地震作用下列车运行状态看做为列车在不平顺的轨道上运行和地震作用下列车在光滑的轨道上运行这两种状态的叠加,利用地震作用下列车静态的方法计算脱轨系数等脱轨指标,并将其安全冗余量作为地震作用下列车静止状态时的脱轨系数限值,从而利用脱轨系数限值来确定高速铁路地震预警阈值.
3) 通过输入6种不同的水平向地震波,台湾集集波、El-Centro波、Kobe波、天津波、汶川卧龙波、Northridge波对车辆-轨道模型进行计算分析,利用脱轨指标的安全冗余量,给出地震作用下列车静态时的不同脱轨系数限值和不同轮重减载率限值相对应的预警阈值,并建议中国高速铁路地震预警阈值设为40 gal.
| [1] |
刘恢先. 唐山大地震震害[M]. 北京: 地震出版社, 1986. LIU Huixian. Tangshan earthquake[M]. Beijing: Seismological Press, 1986. |
| [2] |
佐藤吉彦.新轨道力学[M].徐涌, 译.北京: 中国铁道出版社, 2001
|
| [3] |
马强, 李山有, 于海英, 等. 高速铁路地震防灾系统的应急处置范围确定[J]. 铁道学报, 2013, 35(6): 110. MA Qiang, LI Shanyou, YU Haiying, et al. Determination of emergency disposal range of earthquake disaster prevention system for high speed railway[J]. Journal of the China Railway Society, 2013, 35(6): 110. DOI:10.3969/j.issn.1001-8360.2013.06.017 |
| [4] |
刘林, 闫贵平, 辛学忠. 京沪高速铁路地震预警系统的方案及关键参数研究[J]. 中国安全科学学报, 2002, 12(4): 75. LIU Lin, YAN Guiping, XIN Xuezhong. Study on schemes and key parameters of seismic alarm system for Beijing-Shanghai express railway[J]. Chinese Safety Science Journal, 2002, 12(4): 75. DOI:10.3969/j.issn.1003-3033.2002.04.018 |
| [5] |
孙利.高速铁路地震预警系统阈值探索[D].大连: 大连理工大学, 2011 SUN Li. Exploration of threshold value of earthquake early warning system for high speed railway[D]. Dalian: Dalian University of Technology, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10141-1011109648.htm |
| [6] |
MIYAMOTO T, ISHID H, MATSUO M. Running safety of railway vehicle as earthquake occurs[J]. Railway Technical Research Institute, Quarterly Reports, 1997, 38(3): 117. |
| [7] |
MIYAMOTO T, MATSUMOTO N, SOGABE M, et al. Full-scale experiment on the dynamic behavior of railway vehicles against heavy track vibration[J]. Journal of Environment and Engineering, 2007, 2(2): 419. |
| [8] |
MIYAMOTO T, ISHID H. Numerical analysis focusing on the running safety of an improved bogie during seismic vibration[J]. Quarterly Report of RTRI, 2008, 49(3): 173. DOI:10.2219/rtriqr.49.173 |
| [9] |
LIDA K, SUZUKI M, MIYAMOTO T, et al. Development of a lateral damper to improve the running safety of railway vehicles during an earthquake[J]. Quarterly Report of RTRI, 2012, 53(1): 34. DOI:10.2219/rtriqr.53.34 |
| [10] |
凌亮, 肖新标, 吴磊, 等. 地震激励下高速列车动态响应与运行安全边界研[J]. 铁道学报, 2012, 34(10): 16. LING Liang, XIAO Xinbiao, WU Lei, et al. Research on dynamic response and operational safety boundary of high-speed train under earthquake excitation[J]. Journal of the China Railway Society, 2012, 34(10): 16. DOI:10.3969/j.issn.1001-8360.2012.10.003 |
| [11] |
LUO Xiu. Study on methodology for running safety assessment of trains in seismic design of railway structures[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(2): 79. DOI:10.1016/j.soildyn.2004.10.005 |
| [12] |
LUO Xiu, MIYAMOTO T. Method for running safety assessment of railway vehicles against structural vibration displacement during earthquakes[J]. Quarterly Report of RTRI, 2007, 48(3): 129. DOI:10.2219/rtriqr.48.129 |
| [13] |
凌亮, 肖新标, 吴磊, 等. 地震波频谱特性对高速列车动态脱轨行为的影响[J]. 工程力学, 2013, 30(1): 384. LING Liang, XIAO Xinbiao, WU Lei, et al. Influence of spectral characteristics of seismic waves on dynamic derailment behavior of high-speed trains[J]. Engineering Mechanics, 2013, 30(1): 384. |
| [14] |
徐鹏.列车-轨道-路基耦合振动及地震条件下行车安全性分析[D].成都: 西南交通大学, 2011 XU Peng. Analysis of train-track-subgrade coupled vibration and seismic conditions for down vehicle safety[D]. Chengdu: Southwest Jiaotong University, 2011 http://www.cnki.com.cn/Article/CJFDTotal-ZGTK201402021.htm |
| [15] |
吴兴文.地震条件下车辆脱轨安全性研究[D].成都: 西南交通大学, 2016 WU Xingwen. Research on vehicle derailment safety under earthquake conditions[D]. Chengdu: Southwest Jiaotong University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10613-1017019208.htm |
| [16] |
NISHIMURA K, TERUMICHI Y, MORIMURA T, et al. Development of vehicle dynamics simulation for safety analyses of rail vehicles on excited tracks[J]. Journal of Computational and Nonlinear Dynamics, 2009, 4(1): 1. |
| [17] |
NISHIMURA K, TERUMICHI Y, MORIMURA T, et al. Experimental study on the vehicle safety by earthquake track excitation with 1/10 scale vehicle and roller rig[J]. Journal of System Design and Dynamics, 2010, 4(1): 226. DOI:10.1299/jsdd.4.226 |
| [18] |
NISHIMURA K, TERUMICHI Y, MORIMURA T, et al. Analytical study on the safety of high speed railway vehicle on excited tracks[J]. Journal of System Design and Dynamics, 2010, 4(1): 211. DOI:10.1299/jsdd.4.211 |
| [19] |
NISHIMURA K, TERUMICHI Y, MORIMURA T, et al. Using full scale experiments to verify a simulation used to analyze the safety of rail vehicles during large earthquakes[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(1). |
| [20] |
国家铁路局.轮轨横向力和垂向力地面测试方法: TB/T 2489—2016[S].北京: 中国铁道出版社, 2010 State Railway Administration. Track side test methods of vertical and lateral wheel-rail forces: TB/T 2489—2016[S]. Beijing: China Railway Press, 2010 |
| [21] |
翟婉明.车辆-道耦合动力学[M].科学出版社, 2015 ZHAI Wanming. Vehicle-track coupled dynamics[M]. Beijing: Science Press, 2015 |
| [22] |
国家铁路局.高速铁路设计规范(试行): TB 10621—2009[S].北京: 中国铁道出版社, 2010 State Railway Administration. Design specification for high speed railway (Trial): TB 10621—2009[S]. Beijing: China Railway Press, 2010 |
 2019, Vol. 51
2019, Vol. 51


