2. 长安大学 公路学院, 西安 710061
2. School of Highway, Chang'an University, Xi'an 710061, China
交通流状态判别作为智能交通系统(ITS)关键技术之一,通过准确的交通流运行状态信息,实时反映道路服务水平,对先进的交通管理系统(ATMS)、先进的出行者信息系统(ATIS)和车辆诱导系统提供策略依据.早期交通流状态判别研究多针对于偶发性交通突发事件的检测,采取的方法有加利福尼亚算法、双指数平滑算法、基于突变理论下的McMaster算法等[1].目前交通流状态判别更多地集中在常发性拥挤方面,常发性拥挤交通流状态判别,主要从状态判别指标、状态判别方法等方面开展.如文献[2]以行程时间参数为基础,构建交通拥挤指数,实现道路拥挤的自动识别;文献[3]利用地点交通流数据和区域交通流数据,并将二者交通特征融合进行分析,展开对城市交通流状态判别;在状态判别方法方面,提出了多种识别算法,如基于BP神经网络的交通流状态判别方法[4],基于支持向量机交通流状态模式识别算法[5],基于聚类方法的交通流状态辨识分析等[6].
聚类分析方法是目前在状态类型划分过程中应用最为广泛的一种,聚类分析是一种无监督式的机器学习算法,在无任何先验信息情况下实现数据间的模式划分.文献[7]借鉴模糊C均值(FCM)聚类算法思想,选择高速公路上收费数据作为分类指标,对交通流状态进行聚类判别;文献[8]以FCM聚类算法思想为基础,通过设置交通参数不同权重情景,提出一种基于参数权重不同条件下的聚类方法,对交通聚类状态进行划分;文献[9-10]以高速公路交通状态聚类划分为研究对象,对比分析3种不同的聚类算法应用性能,由聚类效果判定K均值聚类算法分类效果最佳.为更好识别状态分类特征,进一步构建聚类组合模型进行分析.文献[11]将K均值聚类模型与多分类SVM模型相结合,通过聚类算法将高速公路状态进行模糊分类处理,再通过SVM模型对每一特征进行分析识别;文献[12]借助机器学习算法对状态类型进行分类,监督学习算法再以已分类信息作为先验信息进行分类识别;文献[13]将动态聚类方法和投影寻踪技术相结合,建立投影指标函数,采用混合蛙跳算法对投影指标函数不断优化,确定最佳投影方向,作为交通流状态判别阈值;文献[14]提出一种新型聚类方法谱聚类,通过谱图对类型进行划分,在划分结果基础上借助随机子空间集成K最近邻思想,组合一种谱聚类与随机子空间集成K近邻(RS-KNN)模型对快速路交通流状态进行判别模型.
然而,上述聚类组合模型对交通流状态的判别在数据量充实条件下效果更好,但由于无检测器装备或检测器设备损坏以致无法获取大量数据时,上述方法对状态类型的判别效果将受到影响.因此,文章提出一种在数据量较少条件下的交通流状态判别方法,即结合灰聚簇与Fisher变换的组合判别模型.灰聚簇与其他聚类模型相比,能够在较少数据下,划分出类内相似度较高,类间相似度较低的类型;而Fisher变换则可利用较少的数据对特征进行辨识,两者结合,能够在数据量较少的条件下对交通流状态特征进行判别.
1 灰聚簇与Fisher变换 1.1 灰聚簇采用灰聚簇(grey clustering,GC)方法,对城市交通流快速路状态进行类型划分,灰聚簇主要涉及两部分内容,一是计算交通流参数间灰色关联度,作为分类的依据;二是确定灰类划分数量,作为分类的强度[15].
1.1.1 灰色关联度灰色关联度可为不同因素之间在数值关系上提供度量标准,在满足整体性、规范性、接近性、偶对对称性等4个基础上,按照以下步骤确定参数灰色关联度,其中定义X={xi|i∈n}为灰色关联子集,xi, j∈X为比较序列对,xi, j(k)为xi, j在k点数值,
步骤1 首先对采集的交通流参数数据按照统计的时间间隔进行粒子区间划分,一般选取5 min间隔作为粒子区间的划分标准,划分形式为[tk tk+1],划分区间的数量n作为初步类型数量n,且类型中心为其本身.
步骤2 确定数据中两两之间灰色系数[16]为
| $ \begin{array}{l} \hat r\left( {{x_i}(k),{x_j}(k)} \right) = \\ \frac{{\mathop {\min }\limits_{j \ne i}^n \left| {{x_i}(k) - {x_j}(k)} \right| + \delta \mathop {\max }\limits_{j \ne i}^n \left| {{x_i}(k) - {x_j}(k)} \right|}}{{\left| {{x_i}(k) - {x_j}(k)} \right| + \delta \mathop {\max }\limits_{j \ne i}^n \left| {{x_i}(k) - {x_j}(k)} \right|}}. \end{array} $ | (1) |
步骤3 由灰色关联系数的平均值确定各因子灰色关联度为
| $ r\left( {{x_i}(k) - {x_j}(k)} \right) = \sum\limits_{k = 1}^m {\frac{{\hat r\left( {{x_i}(k) - {x_j}(k)} \right)}}{m}} . $ | (2) |
步骤4 进一步确定灰色初始相似度矩阵为
| $ \mathit{\boldsymbol{R}} = \left\{ {\begin{array}{*{20}{c}} 1&{{r_{1,2}}}& \cdots &{{r_{1,n}}}\\ {{r_{2,1}}}&1& \cdots &{{r_{2,n}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{r_{n,1}}}&{{r_{n,2}}}& \cdots &1 \end{array}} \right\}. $ | (3) |
步骤5 由灰色关联度计算结果,确定类与类间关联度最为接近的两类,合并为新类型,则总类型数量减少一类.
步骤6 确定新类型与原类型之间关联度为
| $ {r_{\left( {pq} \right)t}} = \frac{{{r_{pt}} + {r_{qt}}}}{2}. $ | (4) |
式中:p、q、t为原类型,pq为合并的新类型,rpt为类型p、t之间关联度,rqt为类型q、t之间关联度,r(pq)t为新类型pq、t之间关联度.
步骤7 确定新关联度后继续进行步骤5、步骤6步骤,按照类型数量划分判别标准,获得最佳分类数量.
1.1.2 灰类划分数量选择统计量RSQ及半偏相关统计量SPRSQ作为灰类型数量划分最佳的标准.统计量RSQ可用来评价类型间合并聚类效果,若CRSQ=1表明所有类型各自为1类,若CRSQ=0表明所有类型合并为1类,这是类型划分的两种极端现象,且认为RSQ值显著减少所对应类型数为最佳分类结果,计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{S_t} = \sum\limits_{i = 1}^{{n_t}} {{{\left( {{\mathit{\boldsymbol{x}}_{it}} - {{\mathit{\boldsymbol{\bar x}}}_t}} \right)}^{\rm{T}}}} \left( {{\mathit{\boldsymbol{x}}_{it}} - {{\mathit{\boldsymbol{\bar x}}}_t}} \right),}\\ {{P_k} = \sum\limits_{t = 1}^k {{S_t}} ,}\\ {M = \sum\limits_{i = 1}^n {{{\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\bar x}}} \right)}^{\rm{T}}}} \left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\bar x}}} \right) = \sum\limits_{i = 1}^n {{{\left\| {\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\bar x}}} \right)} \right\|}^2}} ,}\\ {{C_{{\rm{RSQ}}}} = 1 - \frac{{{P_k}}}{M}.} \end{array}} \right. $ | (5) |
半偏相关统计量SPRSQ为统计量RSQ的差值,且该统计量值越大表明上一次合并效果更好,计算公式为
| $ \left\{ \begin{array}{l} {S_{p,q,r}} = \sum\limits_{i \in {G_{P.Q.R}}} {{{\left( {{\mathit{\boldsymbol{x}}_i} - {{\mathit{\boldsymbol{\bar x}}}_{p,q,r}}} \right)}^{\rm{T}}}} \left( {{\mathit{\boldsymbol{x}}_i} - {{\mathit{\boldsymbol{\bar x}}}_{p,q,r}}} \right),\\ {{\bar x}_r} = \frac{{{n_p}{{\mathit{\boldsymbol{\bar x}}}_p} + {n_q}{{\mathit{\boldsymbol{\bar x}}}_q}}}{{{n_r}}} = \frac{{{n_p}{{\mathit{\boldsymbol{\bar x}}}_p} + {n_q}{{\mathit{\boldsymbol{\bar x}}}_q}}}{{{n_p} + {n_q}}},\\ {W_{pq}} = {S_r} - {S_p} - {S_q} = \frac{{{n_p}{n_q}}}{{{n_{\rm{r}}}}}{\left( {{{\bar x}_p} - {{\bar x}_q}} \right)^{\rm{T}}}\left( {{{\bar x}_p} - {{\bar x}_q}} \right),\\ {C_{{\rm{SPRSQ}}}} = \frac{{{W_{pq}}}}{M}. \end{array} \right. $ | (6) |
式中:St为类内离差平方和,此值越小相似度越近;Pk为所分k类离差平方总和;Sp, q, r分别为特征向量Gp、Gq类型及二者合并为Gr类型后的类内离差平方和;Wpq为合并新类型后离差平均和增量.
1.2 Fisher变换Fisher判别[17]源于20世纪30年代,通过将多维指标数据投影至某一方向中,得到一个由p维变量组成的线性函数,该线性函数按照增大不同类间函数差异值,缩小同类内各点函数差异值的方式,确保类与类间尽可能区分,并由亲疏程度判别未知数据归属.文中采用多总体Fisher判别结构,是在两总体Fisher判别结构基础上扩展而来,计算公式[18]为
| $ y(x) = {c_1}{x_{1q}} + \cdots + {c_p}{x_{pq}} = \sum\limits_{i = 1}^p {{c_i}} {x_{iq}}. $ | (7) |
式中:xpq为在第p维变量q组数据的观测值,c1, …, cp为p维变量所对应的判别系数,y(x)为多维转变为低维的判别函数值.
进一步可以获得在G1, G2, …, Gk总体下,判别函数y(Gi)(x)值,计算公式为
| $ {y^{\left( {{G_i}} \right)}}(x) = {c_1}x_{1q}^{\left( {{G_i}} \right)} + \cdots + {c_p}x_{pq}^{\left( {{G_i}} \right)} = \sum\limits_{i = 1}^p {{c_i}} x_{iq}^{\left( {{G_i}} \right)}. $ | (8) |
为确定y(Gi)(x)判别函数的具体形式,首先确定判定系数ci值,则
| $ \mathit{\boldsymbol{I}} = \frac{{\sum\limits_{i = 1}^k {{n_i}} {{\left( {{{\bar y}^{\left( {{G_i}} \right)}} - \frac{1}{k}\sum\limits_{i = 1}^k {{{\bar y}^{\left( {{G_i}} \right)}}} } \right)}^2}}}{{\sum\limits_{i = 1}^k {\sum\limits_{q = 1}^n {{{\left( {y_q^{\left( {{G_i}} \right)} - {{\bar y}^{\left( {{G_i}} \right)}}} \right)}^2}} } }}. $ | (9) |
由式(9)按照类间差值越大、类内差值越小的基本原则,计算max I所对应的特征值,将特征值对应的特征向量,作为判别函数的最佳系数ci.结合式(8),并对式(9)分子分母单独分析,得到
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{B}} = \sum\limits_{i = 1}^k {{n_i}} \left( {{{\mathit{\boldsymbol{\bar x}}}^{\left( {{G_i}} \right)}} - \mathit{\boldsymbol{\bar x}}} \right){\left( {{{\mathit{\boldsymbol{\bar x}}}^{\left( {{G_i}} \right)}} - \mathit{\boldsymbol{\bar x}}} \right)^{\rm{T}}},\\ \mathit{\boldsymbol{E}} = \sum\limits_{i = 1}^k {\sum\limits_{q = 1}^n {\sum\limits_{p = 1}^m {\left( {\mathit{\boldsymbol{x}}_{pq}^{\left( {{G_i}} \right)} - \mathit{\boldsymbol{\bar x}}_p^{\left( {{G_i}} \right)}} \right)} } } {\left( {\mathit{\boldsymbol{x}}_{pq}^{\left( {{G_i}} \right)} - \mathit{\boldsymbol{x}}_p^{\left( {{G_i}} \right)}} \right)^{\rm{T}}},\\ \mathit{\boldsymbol{I}} = \frac{{\mathit{\boldsymbol{cB}}{\mathit{\boldsymbol{c}}^{\rm{T}}}}}{{\mathit{\boldsymbol{cE}}{\mathit{\boldsymbol{c}}^{\rm{T}}}}}. \end{array} \right. $ | (10) |
对式(10)求系数c的偏导数,并令偏导数值取0所对应的ci为最佳系数,即
| $ \frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial \mathit{\boldsymbol{c}}}} = \partial \left( {\frac{{\mathit{\boldsymbol{cB}}{\mathit{\boldsymbol{c}}^{\rm{T}}}}}{{\mathit{\boldsymbol{cE}}{\mathit{\boldsymbol{c}}^{\rm{T}}}}}} \right)/\partial \mathit{\boldsymbol{c}} = \frac{{2\mathit{\boldsymbol{Bc}}}}{{\mathit{\boldsymbol{cE}}{\mathit{\boldsymbol{c}}^{\rm{T}}}}} - \frac{{2\mathit{\boldsymbol{IEc}}}}{{\mathit{\boldsymbol{cE}}{\mathit{\boldsymbol{c}}^{\rm{T}}}}} = 0. $ | (11) |
由式(11)可知Bc=IEc中I、c分别作为B, E广义特征根及所对应的特征向量,从而确定判别函数.但由于所研究Fisher判别分类组数为k,则仅一个判别函数并不能满足种类判别需求,因此按照非零特征根的从大到小依次对应的特征向量作为构建的判别函数系数,构建m(m<k)个判别函数.其中,特征根的数量需要满足累计判别效率达到85%以上的要求,特征根累计判别效率的计算为
| $ \sum\limits_{i = 1}^k {{\lambda _i}} /\sum\limits_{i = 1}^p {{\lambda _i}} \le 85\% . $ | (12) |
面对多种类样本数据情景,对新样本归属类型进行判定,应遵循规则:设yi(x)为第i个线性判别函数,计算新样本与以确定样本yi(Gk)(xk)中距离之差,差值最小者为新样本归属的类型.新样本归属类型计算公式为
| $ \left\{ \begin{array}{l} d\left( {x,{G_k}} \right) = \sum\limits_{i = 1}^r {{{\left( {{y_i}(x) - y_i^{\left( {{G_k}} \right)}\left( {{{\bar x}_k}} \right)} \right)}^2}} ;\\ d\left( {x,{G_t}} \right) = \mathop {\min }\limits_{1 \le j \le k} d\left( {x,{G_k}} \right),\;\;\;\;x \in {G_t}. \end{array} \right. $ | (13) |
将灰聚簇分类结果采用多总体Fisher变换分析,构建GC-Fisher判别模型,该模型流程分为以下步骤.
步骤1 选取交通状态参数中交通量Q、速度v、占有率O三个参数作为判别的特征量,采集相关数据并进行统一的标准化处理,处理方式为
| $ x_{ij}^\prime = \frac{{{x_{ij}} - {x_{j,{\rm{min}}}}}}{{{x_{j,{\rm{max}}}} - {x_{j,{\rm{min}}}}}}. $ | (14) |
式中:xj, max, xj, min分别表示特征量j在采集序列中的最大值和最小值,xij′为归一化后的数值.
步骤2 由参数之间灰色关联度确定类型间合并依据,由统计量RSQ、SPRSQ值,确定状态划分的最佳分类数量k,可设置相对应标签加以区分,如状态类型1, 2, …, k等.
步骤3 通过灰聚簇已确定总体样本类型数量为k,选择标准化后的交通量Q、速度v、占有率O作为三维指标,每一维指标选取n个样本数目,构造Fisher变换训练集,训练集输出多总体下的Fisher线性判别映射函数.
步骤4 采用实验数据训练上述GC-Fisher模型,输入新样本类型的三维指标数据,通过应用多总体下的Fisher线性判别映射函数,由亲疏远近程度差异输出最终样本数据状态归属类型.
3 实例分析 3.1 数据描述选择长沙市湘府路作为研究对象,采集交通量Q、速度v、占有率O连续5 d工作日(2016年11月14日至2016年11月18日)17:00—20:00数据,其中设置连续前4 d的数据作为训练数据,第5 d数据作为测试数据进行分析.数据采集间隔为5 min,则连续的3 h数据共划分36个研究单元,统计结构形式为[tk tk+1],其中k∈[0, 36].
| $ \left\{ \begin{array}{l} {q_i} = \sum\limits_{j = 1}^n {{q_{ij}}} ,\\ {v_i} = \left( {\sum\limits_{j = 1}^n {{q_{ij}}} {v_{ij}}} \right)/\sum\limits_{j = 1}^n {{q_{ij}}} ,\\ {O_i} = \left( {\sum\limits_{j = 1}^n {{q_{ij}}} {o_{ij}}} \right)/\sum\limits_{j = 1}^n {{q_{ij}}} . \end{array} \right. $ | (15) |
式中:qi、vi、Oi分别代表断面i上的流量、速度、占有率,j为断面车道编号,n为断面车道数量.
通过式(15)可将采集的车道交通流数据转化为断面交通流数据.
3.2 基于灰聚簇的状态类型划分对采集的交通量Q、速度v、占有率O数据进行标准化处理,在处理结果基础上获得对应参数的灰色关联度矩阵.灰色关联矩阵RQ、Rv、RO分别为
| $ {\mathit{\boldsymbol{R}}_Q} = \left[ {\begin{array}{*{20}{c}} 1&{0.65}& \cdots &{0.44}\\ {0.65}&1& \cdots &{0.58}\\ \vdots & \vdots & \vdots & \vdots \\ {0.44}&{0.58}& \cdots &1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_v} = \left[ {\begin{array}{*{20}{c}} 1&{0.59}& \cdots &{0.33}\\ {0.59}&1& \cdots &{0.45}\\ \vdots & \vdots & \vdots & \vdots \\ {0.33}&{0.45}& \cdots &1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{R}}_O} = \left[ {\begin{array}{*{20}{c}} 1&{0.55}& \cdots &{0.51}\\ {0.55}&1& \cdots &{0.61}\\ \vdots & \vdots & \vdots & \vdots \\ {0.51}&{0.61}& \cdots &1 \end{array}} \right] $ |
计算统计量RSQ及半偏相关统计量SPRSQ,并观察其变化趋势,确定各参数最佳分类数量.
图 1为Q、v、O统计量RSQ及半偏相关统计量SPRSQ分类变化信息,由统计量判定标准,确定最佳分类结果.其中,统计量RSQ判定标准为该值显著减少时所对应的分类数即是分类数的最佳结果;而统计量SPRSQ则选择该值最大时的上一次合并类型数目作为最佳分类结果.结合图 1统计量RSQ和SPRSQ值变化,及二者判定标准,确定交通流状态类型最佳划分数量为4.
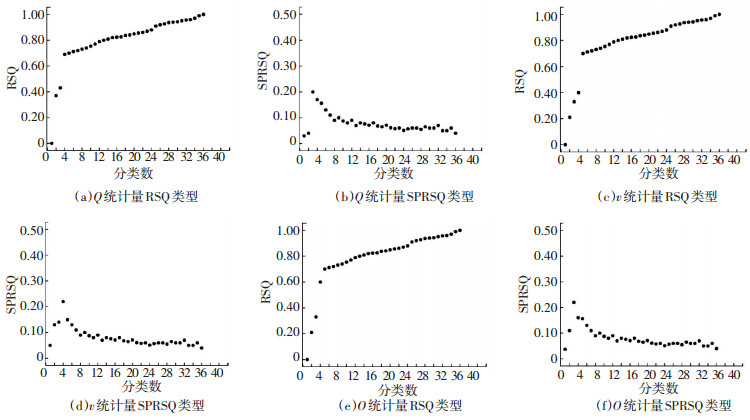
|
图 1 分类结果图 Fig. 1 Diagram of classification result |
在确定4种状态聚类类型的基础上,借助R语言软件平台,获取采集数据Q、v、O在每一类型下的聚类源,其中表 1表示4种不同状态下Q、v、O的聚类源.进一步可由4种状态聚类结果,获得每一状态下参数之间对应变化关系,主要包括Q-v-O、Q-v、Q-O及v-O等变化关系,如图 2所示,根据变化特征可明显判断聚类簇与簇之间界限特征.
| 表 1 不同状态下各参数聚类中心 Tab. 1 Clustering centers of various parameters under different conditions |
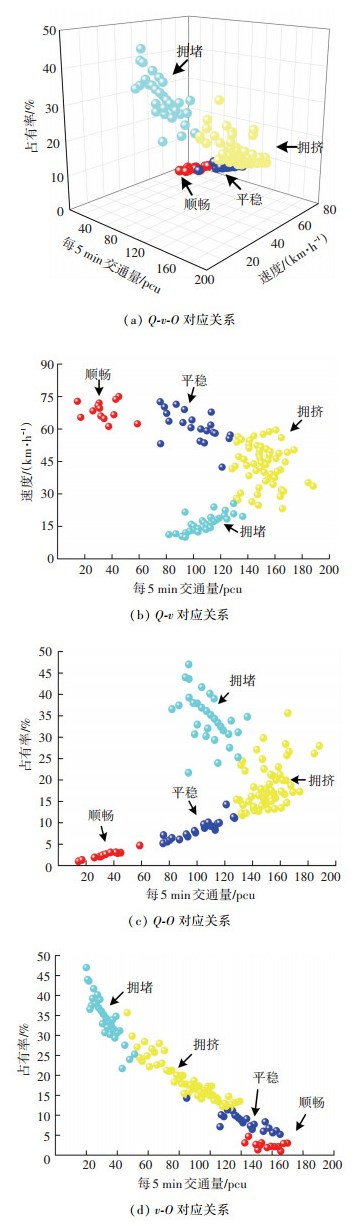
|
图 2 参数变化特征 Fig. 2 Parameter change characteristics |
图 2信息能够表明簇与簇间分类特征较为明显,其中顺畅状态下,交通量总体水平较少,车辆间干扰能力较弱,占有率低,车辆运行处于自由行驶状态;平稳状态下,随着交通量数量增加,车辆间干扰程度加深,占有率和速度分别呈现升高和下降趋势;拥挤状态下,车辆间干扰程度进一步加剧,交通量增加速度缓慢,占有率上升和速度下降的趋势明显;拥堵状态下,车辆间运行受到严重程度干扰,交通量减小,占有率急剧升高,速度急剧下降,交通流运行呈现极不稳定状态.因此,通过灰聚簇划分的状态类型能够很好表征交通流在不同阶段下运行特征.
将每一时段对应状态类型归类之后,则可判断连续5 d在17:00—20:00时间段中交通流状态变化趋势.分别定义3个坐标轴代表信息,x轴表示一天之内状态变化趋势,选择每5 min作为一个单元,将17:00—20:00划分为1-36个整数单元;y轴表示一周中对应的日期;z轴表示4种状态类型,用编号1、2、3、4表示.由图 3连续5 d状态类型变化趋势,sl可发现变化特征具有一定相似性,整体呈现“凸型”变化,从状态2逐渐过渡为状态4,再由状态4逐渐变为状态1,变化过程中虽存在不同程度波动,但整体较为稳定,符合交通流变化规律特征,因此,采用灰聚簇对状态类型划分具有一定有效性.
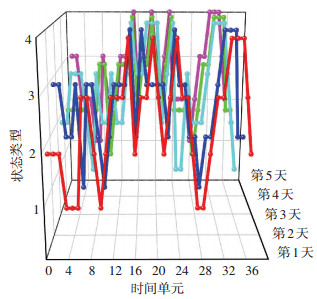
|
图 3 每天交通流状态变化趋势图 Fig. 3 Diagram of daily traffic flow status trend |
选择前4 d状态数据作为基础构建训练集,对状态类型的判别展开分析.根据训练数据集状态类型聚簇结果,确定样本总体类型为4,指标维度p为3,为交通量Q、速度v、占有率O,构建Fisher(4, 3)转换模型的判别函数,其中训练集分类结果见表 2.
| 表 2 训练集样本数据类统计量(标准化后) Tab. 2 Statistical data of training set sample (after standardization) |
由表 2分别获得4组样本类型的均值和标准差,经Fisher转化得到每一样本类型下的yi(Gk)(xk)值,其中转换方式为
| $ \left\{ \begin{array}{l} y_i^{\left( {{G_1}} \right)} = - 1.10{Q_i} + 213.01{v_i} + 205.89{O_i} - 100.42,\\ y_i^{\left( {{G_2}} \right)} = 109.36{Q_i} + 187.03{v_i} + 199.92{O_i} - 130.44,\\ y_i^{\left( {{G_3}} \right)} = 60.45{Q_i} + 173.26{v_i} + 226.01{O_i} - 108.24,\\ y_i^{\left( {{G_4}} \right)} = 62.7{Q_i} + 208.08{v_i} + 205.46{O_i} - 115.62. \end{array} \right. $ | (16) |
转换方式确定之后,需进一步确定判别函数.训练数据集中分类组数k为4,因此需要构建多个判别函数才能保证样本类型准确识别.共确定相对应的非零特征根共3个,根值分别为6.117、4.26、2.629,其相对应的方差为47.03%、32.75%、20.21%,满足85%以上累计判别效率要求.由此,需要构建3个判别函数数量,由特征根值得到标准化典型判别式函数系数,判别函数为
| $ \left\{ \begin{array}{l} F1 = 0.894{Q_i} + 0.49{v_i} - 0.031{O_i},\\ F2 = - 0.421{Q_i} + 0.487{v_i} + 1.676{O_i},\\ F3 = - 0.040{Q_i} - 0.495{v_i} + 1.746{O_i}. \end{array} \right. $ | (17) |
测验数据由式(17)得到3种判别函数值,与4种样本类型的转换平均值y(G1)、y(G2)、y(G3)、y(G4)处理得到距离差,选择距离差值的和最小作为归属类型.
3.4 模型性能测试选择第5 d数据进行分析判断构建测验集,测验GC-Fisher模型对交通流状态类型判别性能效果.本文针对模型性能测试采用对比分析方式,选择K-SVM组合判别模型作为比较,K-SVM模型RBF核函数参数定值取2.2,惩罚系数确定取10.5[7].以矩阵形式展示判别效果信息,其中主对角线表示正确判别类别信息,非主对角线表示误判类别信息,数字表示判别的个数,百分比指该个体数量占总体数量比重,灰色方格中上面百分比为判别率,下面百分比为误判率.
结合图 4提供的判别效果比较信息,两种判别模型均存在误判情况.当所采集的数据量较少时,采用GC-Fisher模型对交通流状态判别率为92%,而K-SVM模型的交通流状态判别率为69%.因此,当数据量较少时,可采用GC-Fisher组合判别模型对交通流状态类型进行判别.
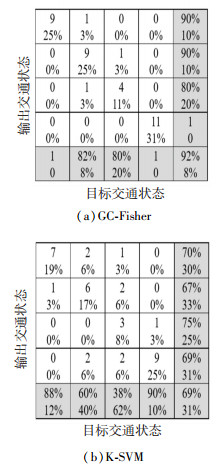
|
图 4 判别效果比较图 Fig. 4 Comparison of discriminant effect |
1) 选择交通量Q、速度v、占有率O作为参数指标,并利用灰聚簇理论中灰色关联度方法,结合统计量RSQ及半偏相关统计量SPRSQ提供的灰类划分标准,确定交通流的4种状态类型,并给出4种状态的聚类源.
2) 以4种交通流状态类型作为总体,提出了一种基于灰聚簇与Fisher变换(GC-Fisher)相结合的状态类型判别模型.
3) 选择“K-SVM”作为比较模型,通过构造数据训练集和测验集,对判别性能进行分析.结果表明GC-Fisher模型的判别率为92%,优于K-SVM模型的判别率69%.因此在数据量较少情况下,GC-Fisher模型对状态类型判别具有更高的判别精度.
4) 仅选择长沙市湘府路作为研究对象较为单一,下一阶段研究仍需从道路空间特征方面着手,选取不同快速路验证模型的普适性,同时仍需进一步设置在不同数据样本量情景下,对GC-Fisher模型的数据样本量敏感程度进行分析.
| [1] |
姜桂艳. 道路交通状态判别技术[M]. 北京: 人民交通出版社, 2004: 66. JIANG Guiyan. Road traffic condition discrimination technology[M]. Beijing: China Communications Press, 2004: 66. |
| [2] |
杨聚芬, 姜桂艳, 李琦. 基于收费数据的高速公路交通拥挤自动判别方法[J]. 哈尔滨工业大学学报, 2014, 46(12): 108. YANG Jufen, JIANG Guiyan, LI Qi. The automatic traffic congestion identification of freeway based on charging date[J]. Journal of Harbin Institute of Technology, 2014, 46(12): 108. DOI:10.11918/j.issn.0367-6234.2014.12.018 |
| [3] |
BHASKAR A, TSUBOTA T, KIEU L M. Urban traffic state estimation: fusing point and zone based data[J]. Transportation Record Part C: Emerging Technologies, 2014, 48: 120. DOI:10.1016/j.trc.2014.08.015 |
| [4] |
巫威眺, 靳文舟, 林培群. 基于BP神经网络的道路交通状态判别方法研究[J]. 交通信息与安全, 2011, 29(4): 71. WU Weitiao, Jin Wenzhou, LIN Peiqun. Research on road traffic condition discrimination based on BP neural network[J]. Traffic Information and Security, 2011, 29(4): 71. DOI:10.3963/j.ISSN1674-4861.2011.04.016 |
| [5] |
于荣, 王国祥, 郑继媛. 基于支持向量机的城市道路交通状态模式识别研究[J]. 交通运输系统工程与信息, 2013(1): 130. YU Rong, WANG Guoxiang, ZHENG Jiyuan. Research on urban road traffic pattern recognition based on support vector machines[J]. Transportation Systems Engineering and Information, 2013(1): 130. DOI:10.3969/j.issn.1009-6744.2013.01.020 |
| [6] |
殷俊杰, 丁宏飞, 薄雾, 等. 基于模糊聚类的城市快速路交通流状态划分[J]. 重庆交通大学学报(自然科学版), 2013, 32(4): 652. YIN Junjie, DING Hongfei, BO Wu, et al. Classification of urban expressway traffic flow based on fuzzy clustering[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2013, 32(4): 652. DOI:10.3969/j.issn.1674-0696.2013.04.25 |
| [7] |
杨庆芳, 马明辉, 梁士栋. 基于收费数据的高速公路交通状态判别方法[J]. 华南理工大学学报(自然科学版), 2014, 42(12): 51. YANG Qingfang, MA Minghui, LIANG Shidong. Distinguishing method of freeway traffic status based on toll data[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(12): 51. DOI:10.3969/j.issn.1000-565X.2014.12.008 |
| [8] |
张亮亮, 贾元华, 牛忠海. 交通状态划分的参数权重聚类方法研究[J]. 交通运输系统工程与信息, 2014, 14(6): 147. ZHANG Liangliang, JIA Yuanhua, NIU Zhonghai. Clustering method of parameter weights for traffic conditioning[J]. Journal of Transportation Systems Engineering and Information, 2014, 14(6): 147. DOI:10.3969/j.issn.1009-6744.2014.06.023 |
| [9] |
AZIMI M, ZHANG Y L. Categorizing freeway flow conditions by using clustering methods[J]. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2010(2173): 105. |
| [10] |
MONTAZERI-GH M, FOTOUHI A. Traffic condition recognition using the k-means clustering method[J]. Scientia Iranica, 2011, 18(4): 930. DOI:10.1016/j.scient.2011.07.004 |
| [11] |
DENG C, WANG F, SHI H M. Real-time freeway traffic state estimation based on cluster analysis and multiclass support vector machine[C]//Proceedings of International Workshop on Intelligent Systems and Applications (ISA). Wuhan: IEEE, 2009
|
| [12] |
ANTONIOU C, KOUTSOPOULOS H N, YANNIS G. Dynamic data-driven local traffic state estimation and prediction[J]. Transportation Research Part C: Emerging Technologies, 2013, 34: 89. DOI:10.1016/j.trc.2013.05.012 |
| [13] |
邴其春, 龚勃文, 杨兆升, 等. 基于投影寻踪动态聚类的快速路交通状态判别[J]. 西南交通大学学报, 2015, 50(6): 1164. BING Qichun, GONG Bowen, YANG Zhaosheng, et al. Expressway traffic state discrimination based on projection pursuit dynamic clustering[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1164. DOI:10.3969/j.issn.0258-2724.2015.06.027 |
| [14] |
商强, 林赐云, 杨兆升, 等. 基于谱聚类与RS-KNN的城市快速路交通状态判别[J]. 华南理工大学学报(自然科学版), 2017, 45(6): 52. SHANG Qiang, LIN Ciyun, YANG Zhaosheng, et al. Identification of urban expressway traffic State based on spectral clustering and RS-KNN[J]. Journal of South China University of Technology (Natural Science Edition), 2017, 45(6): 52. DOI:10.3969/j.issn.1000-565X.2017.06.009 |
| [15] |
田民, 刘思峰, 卜志坤. 灰色关联度算法模型的研究综述[J]. 统计与决策, 2008(1): 24. TIAN Min, LIU Sifeng, BU Zhikun. A review of research on grey correlation algorithm model[J]. Statistics and Decision, 2008(1): 24. |
| [16] |
李善梅, 徐肖豪, 王超, 等. 基于灰色聚类的交叉航路拥挤识别方法[J]. 西南交通大学学报, 2015, 50(1): 189. LI Shanmei, XU Xiaohao, WANG Chao, et al. Congestion identification of crossing air routes based on grey clustering method[J]. Journal of Southwest Jiaotong University, 2015, 50(1): 189. DOI:10.3969/j.issn.0258-2724.2015.01.028 |
| [17] |
TANG W J, GONG F, DONG R R, et al. Face recognition based on the fusion of wavelet packet sub-images and fisher linear discriminant[J]. Multimedia Tools and Applications, 2017, 76: 22725. |
| [18] |
YE H S, LI Y J, CHEN C. Fast Fisher discriminant analysis with randomized algorithms[J]. Pattern Recognition, 2017, 72: 82. DOI:10.1016/j.patcog.2017.06.029 |
 2019, Vol. 51
2019, Vol. 51


