2. 哈工大(张家口)工业技术研究院, 河北 张家口 075421
2. Harbin Institute of Technology at Zhangjiakou, Zhangjiakou 075421, Hebei, China
琼斯矩阵是描述介质输入输出关系的二阶矩阵[1-2],同时也是分析光学效应的一种有效手段[3-5].以往,介质琼斯矩阵以物理属性均匀为前提.如此,其非对角元素或者是纯实数,比如磁光介质,或者是纯虚数,比如电光、弹光和热光介质等.扭转向列液晶的实验研究[6-7]表明,施加的电压较大时,液晶材料的物理属性不再均匀,琼斯矩阵非对角元素变成了实部、虚部皆有的复数.无独有偶,磁光效应[8]的实验研究表明,在不均匀磁场的作用下,磁光玻璃的物理属性也会变得不均匀,琼斯矩阵非对角元素也被复数化.
上述两个实验表明,电场和磁场可使介质的物理属性变得不均匀,表现为琼斯矩阵非对角元素的复数化,意味着光波在介质中的传播过程将有所改变.
为有效刻画光的传播过程,有关研究论文对物理属性不均匀介质琼斯矩阵的解析模型进行了研究.文献[7]基于多层模型推导了扭转向列液晶材料琼斯矩阵的解析式,由此计算的相移差更接近实验结果.基于微元分析法,文献[9-10]推导了磁光玻璃的琼斯矩阵,指出此时的相移差是光程上全部微元相移差的加权积分.与均匀介质的琼斯矩阵相比,上述两项研究更贴近物理属性不均匀介质的情况,不足是都具有一定的近似性,构建的琼斯矩阵尚未包含专门描述介质物理属性不均匀情况的物理参量.
不只电场和磁场,任何物理场都有可能使介质的物理属性变得不均匀.针对任意物理场作用导致的物理属性不均匀的介质,基于介质张量的一般性模型,本文采用微元分析方法探究了琼斯矩阵非对角元素复数化的原因;采用酉变换方法没有近似地建立了由介质相移差、介质感应角和介质不均匀角3个物理参量描述的琼斯矩阵解析模型,其中的介质不均匀角是专门刻画介质物理属性不均匀的物理参量.磁光介质的物理实验和数值仿真验证了本文提出的琼斯矩阵解析式的正确性与合理性.
1 感应不均匀介质在物理场作用下,介质的琼斯矩阵非对角元素可能是实部、虚部兼备的复数,这样的介质在本文中被称为感应不均匀介质.均匀介质受物理场作用表现出不均匀性的现象被称为感应不均匀,感应不均匀现象源自本征坐标系沿光程的不守恒,致使光的传播过程与在均匀介质中有所不同.
1.1 截面张量在电场、磁场、应力场或温度场等物理场的作用下,介质张量(介电张量或逆介电张量)是介质固有张量和物理场产生的感应张量的组合.为避免固有双折射,光波法矢量沿介质光轴,本文称之为z轴.与z轴正交的介质截面,数学模型是二阶张量的平面部分,本文称之为截面张量,即
| $ \boldsymbol{\epsilon}(\mathit{z}) = {\mathit{\boldsymbol{\varepsilon }}_o} + \mathit{\boldsymbol{\delta }}(z). $ | (1) |
其中:εo为截面固有张量,是介电常数εo构成的对角型常数张量εo=diag(εo, εo),δ(z)为物理场作用产生的截面感应张量为
| $ \mathit{\boldsymbol{\delta }}\left( z \right) = \left[ {\begin{array}{*{20}{c}} {{\delta _{\rm{a}}}\left( z \right)}&{k{\delta _{\rm{w}}}\left( z \right)}\\ {\hat k{\delta _{\rm{w}}}\left( z \right)}&{{\delta _{\rm{b}}}\left( z \right)} \end{array}} \right],k \in \left\{ {1,{\rm{j}}} \right\}. $ | (2) |
式(2)是涵盖各种光学效应的一般性的截面感应张量表达式.对实对称感应张量,k=1,如电光、弹光和热光等光学效应;对共轭转置对称的感应张量,k=j,如磁光效应.
1.2 截面感应角截面张量
| $ {\lambda _ \pm }\left( z \right) = {\varepsilon _{\rm{o}}} + {\delta _\nabla }\left( z \right) \pm \sqrt {\delta _\Delta ^2\left( z \right) + \delta _{\rm{w}}^2\left( z \right)} . $ | (3) |
其中δ
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _\nabla }\left( z \right) = \frac{1}{2}\left( {{\delta _{\rm{a}}}\left( z \right) + {\delta _{\rm{b}}}\left( z \right)} \right),}\\ {{\delta _\Delta }\left( z \right) = \frac{1}{2}\left( {{\delta _{\rm{a}}}\left( z \right) - {\delta _{\rm{b}}}\left( z \right)} \right).} \end{array}} \right. $ | (4) |
截面张量
| $ \mathit{\boldsymbol{U}}\left( z \right) = \left[ {\begin{array}{*{20}{c}} {k\cos \frac{{\alpha \left( z \right)}}{2}}&{ - k\sin \frac{{\alpha \left( z \right)}}{2}}\\ {\sin \frac{{\alpha \left( z \right)}}{2}}&{\cos \frac{{\alpha \left( z \right)}}{2}} \end{array}} \right]. $ | (5) |
这里
| $ \alpha \left( z \right) = {\tan ^{ - 1}}\frac{{{\delta _{\rm{w}}}\left( z \right)}}{{{\delta _\Delta }\left( z \right)}}. $ | (6) |
角度α(z)仅由截面感应张量的分量决定,表达了物理场对本征矩阵U(z)的影响.本文称其为截面感应角.
1.3 感应不均匀介质截面感应角α(z)有3种基本情况:1)物理场对介质的作用均匀,δw(z)和δΔ(z)守恒,截面感应角α(z)守恒. 2)物理场对介质的作用不均匀,但δw(z)或δΔ(z)恒零,截面感应角α(z)或为0°,或为90°,依然守恒. 3)物理场对介质的作用不均匀,但δw(z)和δΔ(z)都不恒零,截面感应角α(z)不守恒.
上述3种情况对应的介质分别是均匀介质、似均匀介质和感应不均匀介质.本征矩阵U(z)即是坐标变换矩阵,而截面感应角α(z)唯一决定了本征矩阵U(z).因此,感应不均匀介质是在物理场作用下本征坐标系不守恒的介质.
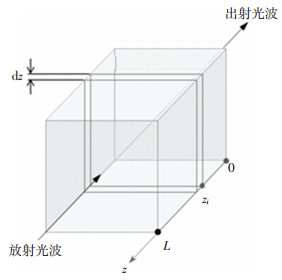
2 琼斯矩阵的非对角元素 2.1 微元级联琼斯矩阵将感应不均匀介质分割为n个微元,微元长度为dz,介质的光程长度为L,如图 1所示.
|
图 1 介质微元的示意 Fig. 1 Schematic diagram of medium micro-element |
微元dz甚小,其截面张量均匀.用符号αi表示截面感应角α(zi),用符号dφi表示微元相移差.坐标zi处的微元琼斯矩阵为
| $ {\mathit{\boldsymbol{J}}_i} = \mathit{\boldsymbol{J}}\left( {{\alpha _i},d{\varphi _i}} \right) = \mathit{\boldsymbol{U}}\left( {{\alpha _i}} \right)\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left( {{\rm{d}}{\varphi _i}} \right){\mathit{\boldsymbol{U}}^H}\left( {{\alpha _i}} \right). $ | (7) |
其中U(αi)为式(6)的本征矩阵,Λ(dφi)为微元相移差矩阵,
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left( {{\rm{d}}{\varphi _i}} \right) = {\rm{diag}}\left( {\exp \left( {{\rm{j}}\frac{{{\rm{d}}{\varphi _i}}}{2}} \right),\exp \left( { - {\rm{j}}\frac{{{\rm{d}}{\varphi _i}}}{2}} \right)} \right), $ | (8) |
这里,dφi为微元相移差,
| $ {\rm{d}}{\varphi _i} = \frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\Delta {n_i}{\rm{d}}z. $ | (9) |
此处,λ为光波的波长,
| $ \Delta {n_i} = \frac{1}{{{n_0}}}\sqrt {\delta _\Delta ^2\left( {{z_i}} \right) + {\delta _{\rm{w}}}\left( {{z_i}} \right)} . $ | (10) |
其中n0为介质的固有折射率.
逆光波方向连乘全部微元琼斯矩阵,极限是光学介质的琼斯矩阵,即
| $ \mathit{\boldsymbol{J}} = \mathop {\lim }\limits_{n \to \infty } \prod\limits_{i = 1}^n \mathit{\boldsymbol{U}} \left( {{\alpha _i}} \right)\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left( {{\rm{d}}{\varphi _i}} \right){\mathit{\boldsymbol{U}}^{\rm{H}}}\left( {{\alpha _i}} \right). $ | (11) |
均匀介质或似均匀介质,截面感应角α(zi)处处相同,本征坐标系守恒.将关系α(zi)≡α代入式(11),得到琼斯矩阵的解析式为
| $ \mathit{\boldsymbol{J}}\left( {\alpha ,\varphi } \right) = \left[ \begin{array}{l} \cos \frac{\varphi }{2} + {\rm{j}}\cos \alpha \sin \frac{\varphi }{2}\;\;\;\;\;k{\rm{jsin}}\alpha \sin \frac{\varphi }{2}\\ \hat k{\rm{jsin}}\alpha \sin \frac{\varphi }{2}\;\;\;\;\;\cos \frac{\varphi }{2} - {\rm{j}}\cos \alpha \sin \frac{\varphi }{2} \end{array} \right]. $ | (12) |
其中
| $ \varphi = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 0}^n {{\rm{d}}{\varphi _i}} = \frac{{{\rm{2 \mathsf{ π} }}}}{\lambda }\int\limits_0^L {\Delta n\left( z \right){\rm{d}}z} . $ | (13) |
式(12)的琼斯矩阵J(α, φ)含两个物理参量α和φ. α为介质感应角,由于介质均匀或似均匀,介质感应角α与截面感应角α(z)相同;φ为描述介质整体的介质相移差.
当k=1时,琼斯矩阵J(α, φ)对称,非对角元素是纯虚数;当k=j时,琼斯矩阵J(α, φ)不对称,非对角元素是纯实数.无论k是1还是j,实部、虚部都不会同时存在.
2.3 感应不均匀介质琼斯矩阵的非对角元素感应不均匀介质的截面感应角不守恒,不能直接由式(11)无近似地推出琼斯矩阵解析式.尽管如此,该式可用来考察琼斯矩阵非对角元素的数域属性.
微元琼斯矩阵Ji=J(αi, dφi)与均匀介质整体琼斯矩阵J(α, φ)元素的数域相同,即
| $ {\mathit{\boldsymbol{J}}_i} = \left[ {\begin{array}{*{20}{c}} {\cos \frac{{{\rm{d}}{\varphi _i}}}{2} + {\rm{j}}\cos {\alpha _i}\sin \frac{{{\rm{d}}{\varphi _i}}}{2}}&{k{\rm{j}}\sin {\alpha _i}\sin \frac{{{\rm{d}}{\varphi _i}}}{2}}\\ {\hat kj\sin {\alpha _i}\sin \frac{{{\rm{d}}{\varphi _i}}}{2}}&{\cos \frac{{{\rm{d}}{\varphi _i}}}{2} - {\rm{j}}\cos {\alpha _i}\sin \frac{{{\rm{d}}{\varphi _i}}}{2}} \end{array}} \right]. $ | (14) |
容易看出,微元琼斯矩阵Ji的对角元素是复数;非对角元素或是实数、或是虚数,不会是实部和虚部兼有的完备复数.
任意两个相邻微元琼斯矩阵的乘积为
| $ \mathit{\boldsymbol{J}}\left( {{\alpha _i},{\rm{d}}{\varphi _i}} \right)\mathit{\boldsymbol{J}}\left( {{\alpha _{i + 1}},{\rm{d}}{\varphi _{i + 1}}} \right) = \left[ {\begin{array}{*{20}{c}} A&{kjC}\\ {\hat kj\hat C}&{\hat A} \end{array}} \right]. $ | (15) |
容易验证,感应不均匀介质,C是实部和虚部兼有的完备复数.原因是本征坐标系沿光程变化,每个截面的本征坐标系与光轴坐标系夹角不守恒.
相邻微元琼斯矩阵的乘积矩阵如此,全部微元琼斯矩阵依次相乘的结果亦然.由于截面本征坐标系不守恒,感应不均匀介质琼斯矩阵的非对角元素是实部、虚部同时存在的完备复数.
3 琼斯矩阵解析式微元琼斯矩阵Ji为酉矩阵.根据酉矩阵的性质可知,级联得到的感应不均匀介质琼斯矩阵J也是酉矩阵,即
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} A&{k{\rm{j}}C}\\ {\hat k{\rm{j}}\hat C}&{\hat A} \end{array}} \right]. $ | (16) |
且满足幺行列式约束
| $ det\left( \mathit{\boldsymbol{J}} \right) = {\left| A \right|^2} + {\left| C \right|^2} = 1. $ | (17) |
式(15)的琼斯矩阵J属于复数域,两个复数A和C对应4个实数ReA, ImA和ReC, ImC,幺行列式约束意味着4个实数不独立,存有冗余.采用酉变换可得到3个独立参量描述的琼斯矩阵解析式.
3.1 琼斯矩阵的本征值命题1 琼斯矩阵J与对角矩阵Λ相似,即
| $ \mathit{\boldsymbol{J}} \sim \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\rm{diag}}\left( {\exp \left( {{\rm{j}}\frac{\varphi }{2}} \right),\exp \left( { - {\rm{j}}\frac{\varphi }{2}} \right)} \right). $ | (18) |
其中
| $ \varphi = 2{\tan ^{ - 1}}\frac{{\sqrt {{\rm{{I{m^2}}}}A + {{\left| C \right|}^2}} }}{{{\rm{Re}}A}}. $ | (19) |
证明 考虑幺行列式约束,式(16)琼斯矩阵的本征方程为
| $ {\lambda ^2} - 2\lambda {\rm{Re}}A + 1 = 0. $ |
解之得
| $ {\lambda _ \pm } = {\rm{Re}}A \pm \sqrt {{\rm{{R{e^2}}}}A - 1} . $ |
幺行列式约束意味着
| $ {\rm{R{e^2}}}A \le 1. $ |
且
| $ 1 - {\rm{R{e^2}}}A = {\rm{I{m^2}}}A + {\left| C \right|^2}. $ |
因此,两个本征值为
| $ {\lambda _ \pm } = {\rm{Re}}A \pm {\rm{j}}\sqrt {{\rm{I}}{{\rm{m}}^2}A + {{\left| C \right|}^2}} . $ |
考虑式(19),得到
| $ {\lambda _ \pm } = \exp \left( { \pm {\rm{j}}\frac{\varphi }{2}} \right). $ |
根据相似矩阵理论,命题1成立.
3.2 琼斯矩阵的本征矩阵命题2 琼斯矩阵J的本征矩阵U为
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {k\cos \frac{\alpha }{2}\exp \left( {{\rm{j}}\sigma } \right)}&{ - k\sin \frac{\alpha }{2}}\\ {\sin \frac{\alpha }{2}}&{\cos \frac{\alpha }{2}\exp \left( { - {\rm{j}}\sigma } \right)} \end{array}} \right]. $ | (20) |
其中
| $ \alpha = {\tan ^{ - 1}}\frac{{\left| C \right|}}{{{\rm{Im}}A}}, $ | (21) |
| $ \sigma = {\tan ^{ - 1}}\frac{{{\rm{Im}}\;C}}{{{\rm{Re}}\;C}}. $ | (22) |
证明 利用式(22),将琼斯矩阵J变形为
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} A&{k{\rm{j}}\left| C \right|\exp \left( {{\rm{j}}\sigma } \right)}\\ {\hat k{\rm{j}}\left| C \right|\exp \left( { - {\rm{j}}\sigma } \right)}&{\hat A} \end{array}} \right], $ |
本征方程为
| $ \left( {\lambda \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{X}} = 0. $ |
这里,X为本征向量.将本征值代入,并考虑式(21),有
| $ \left[ {\begin{array}{*{20}{c}} { - \cos \alpha \pm 1}&{ - k\sin \alpha \exp \left( {{\rm{j}}\sigma } \right)}\\ { - \hat k\sin \alpha \exp \left( { - {\rm{j}}\sigma } \right)}&{\cos \alpha \pm 1} \end{array}} \right]{\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_1}}\\ {{\mathit{\boldsymbol{X}}_2}} \end{array}} \right]^{\left( \pm \right)}} = 0. $ |
求得两个本征矢量:
| $ {\left[ {\begin{array}{*{20}{l}} {{X_1}}\\ {{X_2}} \end{array}} \right]^{\left( + \right)}} = \left[ {\begin{array}{*{20}{l}} {k\sin \alpha \exp ({\rm{j}}\sigma )}\\ { - (\cos \alpha - 1)} \end{array}} \right], $ |
| $ {\left[ {\begin{array}{*{20}{l}} {{X_1}}\\ {{X_2}} \end{array}} \right]^{\left( - \right)}} = \left[ {\begin{array}{*{20}{l}} {k(\cos \alpha - 1)}\\ {\sin \alpha \exp ( - {\rm{j}}\sigma )} \end{array}} \right]. $ |
注意到
| $ \cos \alpha - 1 = - 2{\sin ^2}\frac{\alpha }{2}, $ |
| $ \sin \alpha = 2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}. $ |
弃公因子
| $ {\left[ {\begin{array}{*{20}{l}} {{X_1}}\\ {{X_2}} \end{array}} \right]^{\left( + \right)}} = \left[ {\begin{array}{*{20}{c}} {k\cos \frac{\alpha }{2}\exp \left( {{\rm{j}}\sigma } \right)}\\ {\sin \frac{\alpha }{2}} \end{array}} \right], $ |
| $ {\left[ {\begin{array}{*{20}{l}} {{X_1}}\\ {{X_2}} \end{array}} \right]^{\left( - \right)}} = \left[ {\begin{array}{*{20}{c}} { - k\sin \frac{\alpha }{2}}\\ {\cos \frac{\alpha }{2}\exp \left( { - {\rm{j}}\sigma } \right)} \end{array}} \right]. $ |
两式合并,命题2成立.
3.3 琼斯矩阵解析式根据矩阵理论,感应不均匀介质的琼斯矩阵为
| $ \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{U}}^{\rm{H}}}. $ | (23) |
将命题1和命题2的结果代入,得到
| $ \mathit{\boldsymbol{J}}(\alpha ,\varphi ,\sigma ) = \left[ {\begin{array}{*{20}{c}} {A(\alpha ,\varphi )}&{k{\rm{j}}C(\alpha ,\varphi ,\sigma )}\\ {\hat kj\hat C(\alpha ,\varphi ,\sigma )}&{\hat A(\alpha ,\varphi )} \end{array}} \right]. $ | (24) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {A(\alpha ,\varphi ) = \cos \frac{\varphi }{2} + {\rm{j}}\cos \alpha \sin \frac{\varphi }{2},}\\ {C(\alpha ,\varphi ,\sigma ) = \sin \alpha \sin \frac{\varphi }{2}\exp ({\rm{j}}\sigma ).} \end{array}} \right. $ | (25) |
与均匀或似均匀介质一样,介质感应角α和介质相移差φ依然是琼斯矩阵J(α, φ, σ)的两个物理参量.与均匀或似均匀介质不一样,感应不均匀介质琼斯矩阵J(α, φ, σ)出现了刻画介质感应不均匀情况的新物理参量:介质不均匀角σ. 3个物理参量相互独立,各自的物理含义清晰,缺一不可.
3.4 形式演换截面张量实对称时,如电光效应、声光效应、弹光效应等,k=1,式(24)的琼斯矩阵为
| $ \begin{array}{l} \mathit{\boldsymbol{J}}(\alpha ,\varphi ,\sigma ) = \\ \left[ {\begin{array}{*{20}{l}} {\cos \frac{\varphi }{2} + {\rm{j}}\cos \alpha \sin \frac{\varphi }{2}}&{{\rm{ jsin }}\alpha \sin \frac{\varphi }{2}\exp ({\rm{j}}\sigma )}\\ {{\rm{j}}\sin \alpha \sin \frac{\varphi }{2}\exp ( - {\rm{j}}\sigma )}&{\cos \frac{\varphi }{2} - {\rm{j}}\cos \alpha \sin \frac{\varphi }{2}} \end{array}} \right]. \end{array} $ | (26) |
截面张量共轭转置对称时,即磁光效应,k=j,琼斯矩阵为
| $ \begin{array}{l} \mathit{\boldsymbol{J}}(\alpha ,\varphi ,\sigma ) = \\ \left[ {\begin{array}{*{20}{l}} {\cos \frac{\varphi }{2} + {\rm{j}}\cos \alpha \sin \frac{\varphi }{2}}&{ - \sin \alpha \sin \frac{\varphi }{2}\exp ({\rm{j}}\sigma )}\\ {\sin \alpha \sin \frac{\varphi }{2}\exp ( - {\rm{j}}\sigma )}&{\cos \frac{\varphi }{2} - {\rm{j}}\cos \alpha \sin \frac{\varphi }{2}} \end{array}} \right]. \end{array} $ | (27) |
如果物理场的分布均匀,σ=0,则琼斯矩阵J简化为式(12),分k=1和k=j两种情况.
4 物理参量积分α,φ和σ是感应不均匀介质琼斯矩阵的3个物理参量,属于介质整体.而α(z)和Δn(z)是属于介质截面的物理参量.本节探讨介质整体和截面物理参量之间的积分关系.
4.1 等相移差微元级联琼斯矩阵以微元相移差相等为准则,将介质划分为n个微元.任意一个等相移差微元的琼斯矩阵Ji, (i=1, 2, …, n)为
| $ {\mathit{\boldsymbol{J}}_i} = \left[ {\begin{array}{*{20}{c}} {{A_i}}&{kj{C_i}}\\ {\hat kj{{\hat C}_i}}&{{{\hat A}_i}} \end{array}} \right]. $ | (28) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{A_i} = \cos \frac{{{\rm{d}}\varphi }}{2} + {\rm{j}}\cos {\alpha _i}\sin \frac{{{\rm{d}}\varphi }}{2},}\\ {{C_i} = \sin {\alpha _i}\sin \frac{{{\rm{d}}\varphi }}{2}.} \end{array}} \right. $ | (29) |
这里,dφ为微元相移差,αi为微元的截面感应角.
逆光波方向,将所有微元级联.忽略
| $ \sin \frac{{{\rm{d}}\varphi }}{2} \to \frac{{{\rm{d}}\varphi }}{2},\cos \frac{{{\rm{d}}\varphi }}{2} \to 1. $ |
则可得到如下的等相移差微元级联琼斯矩阵
| $ \mathit{\boldsymbol{J}} = \prod\limits_{i = 1}^n {{J_i}} = \left[ {\begin{array}{*{20}{c}} A&{k{\rm{j}}C}\\ {\hat k{\rm{j}}\hat C}&{\hat A} \end{array}} \right]. $ | (30) |
其中
| $ \left\{ \begin{array}{l} A = 1 - \frac{1}{4}\sum\limits_{i = 2}^n {\sum\limits_{j = 1}^{i - 1} {\cos } } \left( {{\alpha _i} - {\alpha _j}} \right){({\rm{d}}\varphi )^2} + \\ \;\;\;\;\;\;{\rm{j}}\frac{1}{2}\sum\limits_{i = 1}^n {\cos {\alpha _i}{\rm{d}}\varphi } ,\\ C = \frac{1}{2}\sum\limits_{i = 1}^n {\sin {\alpha _i}{\rm{d}}\varphi } + {\rm{j}}\frac{1}{4}\sum\limits_{i = 2}^n {\sum\limits_{j = 1}^{i - 1} {\sin } } \left( {{\alpha _i} - {\alpha _j}} \right){({\rm{d}}\varphi )^2}. \end{array} \right. $ | (31) |
式(30)的琼斯矩阵与式(24)的相同.在
| $ \left\{ {\begin{array}{*{20}{l}} {\varphi \cos \alpha = \sum\limits_{i = 1}^n {\cos {\alpha _i}{\rm{d}}\varphi } ,}\\ {\varphi \sin \alpha \cos \sigma = \sum\limits_{i = 1}^n {\sin {\alpha _i}{\rm{d}}\varphi } ,}\\ {\varphi \sin \alpha \sin \sigma = \frac{1}{2}\sum\limits_{i = 2}^n {\sum\limits_{j = 1}^{i - 1} {\sin } } \left( {{\alpha _i} - {\alpha _j}} \right){{({\rm{d}}\varphi )}^2}.} \end{array}} \right. $ | (32) |
命题3感应不均匀介质,介质相移差φ为截面感应张量对角分量差均值的积分,即
| $ \varphi = \frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda {n_0}}}\frac{1}{{\cos {\alpha _0}}}\int\limits_0^L {{\delta _\Delta }(z){\rm{d}}z} . $ | (33) |
介质感应角α的正弦函数为截面感应张量非对角分量的积分为
| $ \sin \alpha = \frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda {n_0}}}\frac{1}{{\varphi \cos {\sigma _0}}}\int\limits_0^L {{\delta _{\rm{w}}}(z){\rm{d}}z} . $ | (34) |
介质不均匀角σ满足双重积分关系,即
| $ sin\sigma = \frac{1}{2}{\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda {n_0}}}} \right)^2}\frac{1}{{\varphi \sin \alpha }}\int\limits_z^L {\int\limits_0^z {\Delta \left( {{z_1},{z_2}} \right){\rm{d}}{z_1}{\rm{d}}{z_2}} } . $ | (35) |
其中Δ(z1, z2)为积差值,即
| $ \Delta \left( {{z_1},{z_2}} \right) = {\delta _{\rm{w}}}\left( {{z_2}} \right){\delta _\Delta }\left( {{z_1}} \right) - {\delta _{\rm{w}}}\left( {{z_1}} \right){\delta _\Delta }\left( {{z_2}} \right). $ | (36) |
证明 式(32)第1式的积分形式为
| $ \varphi \cos \alpha = \int\limits_0^L {\cos \alpha (z)\frac{{{\rm{d}}\varphi }}{{{\rm{d}}z}}{\rm{d}}z} , $ |
而
| $ \frac{{{\rm{d}}\varphi }}{{{\rm{d}}z}} = \frac{{2{\rm{ \mathsf{ π} }}}}{\lambda }\Delta n(z). $ | (37) |
由于
| $ \cos \alpha (z) = \frac{{{\delta _\Delta }(z)}}{{{n_0}\Delta n(z)}}. $ |
故
| $ \varphi \cos \alpha = \frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda {n_0}}}\int\limits_0^L {{\delta _\Delta }(z){\rm{d}}z} . $ |
于是,式(33)成立.
式(32)第2式的积分形式为
| $ \varphi \sin \alpha \cos \sigma = \int\limits_0^L {\sin \alpha (z)\frac{{{\rm{d}}\varphi }}{{{\rm{d}}z}}{\rm{d}}z} . $ |
由于
| $ \sin \alpha (z) = \frac{{{\delta _{\rm{w}}}(z)}}{{{n_0}\Delta n(z)}}, $ |
并考虑式(37),有
| $ \varphi \sin \alpha \cos \sigma = \frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda {n_0}}}\int\limits_0^L {{\delta _{\rm{w}}}(z){\rm{d}}z} . $ |
因此,式(34)成立.
式(32)第3式的积分形式为
| $ \begin{array}{l} 2\varphi \sin \alpha \sin \sigma = \\ \int\limits_z^L {\int\limits_0^z {\sin \left( {\alpha \left( {{z_2}} \right) - \alpha \left( {{z_1}} \right)} \right)\frac{{{\rm{d}}\varphi }}{{{\rm{d}}{z_1}}}\frac{{{\rm{d}}\varphi }}{{{\rm{d}}{z_2}}}{\rm{d}}{z_1}{\rm{d}}{z_2}} } . \end{array} $ |
注意到
| $ \begin{array}{l} \sin \left( {\alpha \left( {{z_2}} \right) - \alpha \left( {{z_1}} \right)} \right) = \\ \;\;\;\;\sin \alpha \left( {{z_2}} \right)\cos \alpha \left( {{z_1}} \right) - \cos \alpha \left( {{z_2}} \right)\sin \alpha \left( {{z_1}} \right). \end{array} $ |
并将上式关系代入,得到
| $ \varphi \sin \alpha \sin \sigma = \frac{1}{2}{\left( {\frac{{2{\rm{ \mathsf{ π} }}}}{{\lambda {n_0}}}} \right)^2}\int\limits_z^L {\int\limits_0^z {\Delta \left( {{z_1},{z_2}} \right){\rm{d}}{z_1}{\rm{d}}{z_2}} } . $ |
所以,式(35)成立.
5 磁光介质的实验验证为验证理论的正确性,本文进行了感应不均匀磁光介质的物理实验和仿真实验.
5.1 物理实验物理实验验证不均匀磁场对磁光介质琼斯矩阵非对角元素数域的影响.
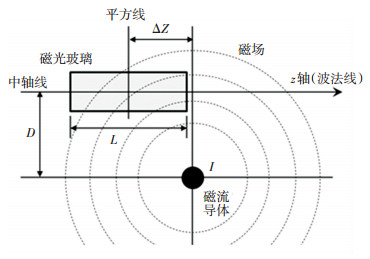
将长度L=0.05 m的磁光玻璃置放在长直载流导体的磁场环境中,如图 2所示.图中,D为磁光玻璃的垂直距离(磁光玻璃中轴线与载流导体的距离),分别取0.02、0.03 m,ΔZ为磁光玻璃的水平距离(平分线与载流导体的距离),取0.025 m~0.025 m. I为载流导体通过的电流,取1 000 A,z轴为光的传播方向.很明显,磁光玻璃处于不均匀空间磁场环境中.
|
图 2 不均匀磁场中的磁光玻璃 Fig. 2 Magnetic glass in non-uniform magnetic field |
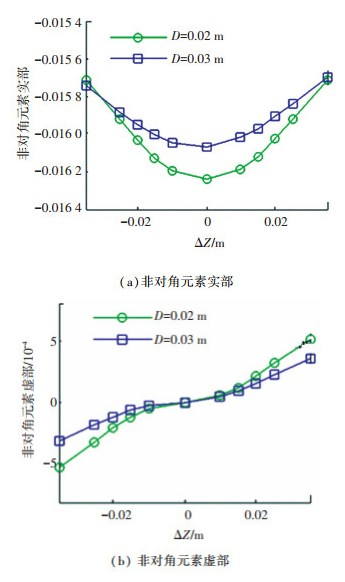
采取光强法[11]测量磁光玻璃琼斯矩阵的元素.磁光玻璃琼斯矩阵J非对角元素测量结果如图 3所示.可以看出,由于磁场分布的不均匀,琼斯矩阵J非对角元素是实部和虚部兼有的完备复数.
|
图 3 琼斯矩阵非对角元素 Fig. 3 The off-diagonal element of Jones matrix |
仿真实验采用磁光玻璃,费尔德常数为80 min/(T·cm),线性双折射恒定为3 min/cm,光源波长为830 nm.
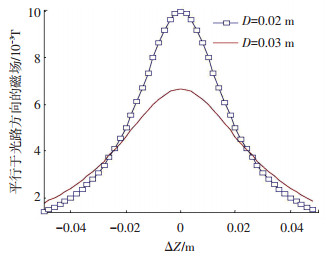
数值仿真依据上文物理实验条件.磁感应强度(与光波方向平行的分量)不均匀分布的仿真情况如图 4所示.
|
图 4 不均匀分布的磁感应强度平行分量 Fig. 4 Distribution of non-uniform magnetic induction |
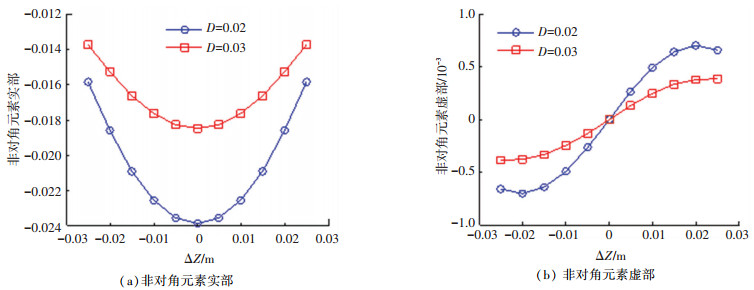
将磁光玻璃分割为105个微元.基于微元琼斯矩阵的级联形式得到介质整体的琼斯矩阵J. 图 5是非对角元素的仿真结果.可以看出,无论是数值的数量级,还是曲线的形状.琼斯矩阵非对角元素的仿真结果与图 3很吻合,说明了仿真的正确性.
|
图 5 琼斯矩阵非对角元素的仿真 Fig. 5 Simulation for the off-diagonal element of Jones matrix |
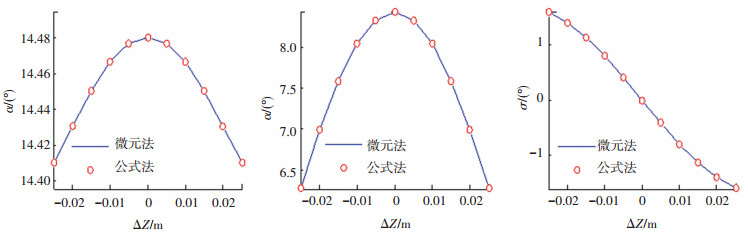
根据式(20)、(21)、(22)计算磁光玻璃的介质相移差φ、介质感应角α和介质不均匀角σ.计算结果如图 6、7曲线所示.采用式(34)、(35)、(36)的积分公式计算磁光玻璃的介质相移差φ、介质感应角α和介质不均匀角σ,计算结果如图 6、7圆点所示.计算数据表明,两者的相对误差在万分之几以内,说明积分公式完好表达了磁光玻璃的感应不均匀情况.

|
图 6 琼斯矩阵物理参量的仿真(D=0.02 m) Fig. 6 Simulation for physical parameters of Jones matrix(D=0.02 m) |
|
图 7 琼斯矩阵物理参量的仿真(D=0.03 m) Fig. 7 Simulation for physical parameters of Jones matrix (D=0.03 m) |
计算表明,当ΔZ=0时,磁光玻璃的介质不均匀角σ为零;当ΔZ≠0时,磁光玻璃的介质不均匀角σ非零,且随着|ΔZ|的增大而增大. 图 6、7的曲线还表明,介质不均匀角σ的绝对值越小,介质相移差φ和介质感应角α越大,反之越小,说明磁场分布越是不均匀,对磁光石玻璃琼斯矩阵的影响就越大.
6 结论1) 物理和仿真实验表明,感应不均匀介质琼斯矩阵的非对角元素是实部和虚部兼而有之的复数.理论研究表明,截面感应角沿光程分布的不均匀是介质琼斯矩阵非对角元素复数化的原因.
2) 基于酉变换,可准确得到用介质相移差、介质感应角和介质不均匀角3个物理参量表达的感应不均匀介质琼斯矩阵解析表达式.其中,介质不均匀角(绝对值)越大,介质相移差和介质感应角越小,反之亦然.介质不均匀角本质上表达了介质的不均匀情况.
3) 推演了感应不均匀介质的3个物理参量的积分关系.其中,介质相移差是截面感应张量对角分量差均值的积分;介质感应角是截面感应张量非对角分量的积分;介质不均匀角是截面感应张量分量积差值的积分.
| [1] |
JONES R C. A new calculus for the treatment of optical systems. I. Description and discussion of the calculus[J]. Journal of the Optical Society of America, 1942, 31(7): 98. |
| [2] |
HURWITZ H, JONES R C. A new calculus for the treatment of optical systems:Ⅱ. Proof of three general equivalence theorems[J]. Journal of the Optical Society of America, 1941, 31(7): 87. |
| [3] |
孙刚, 金世龙. 双折射晶体琼斯矩阵分析[J]. 应用光学, 2005(4): 17. SUN Gang, JIN Shilong. Analysis of Jones matrix of birefringent crystal[J]. Applied Optics, 2005(4): 17. DOI:10.3969/j.issn.1002-2082.2005.04.005 |
| [4] |
赵一男, 郭志忠, 白德宇. 电光晶体的分布参数琼斯矩阵[J]. 光电子技术, 2015, 35(2): 101. ZHAO Yinan, GUO Zhizhong, BAI Deyu. Research on Jones matrix of distributed parameter of electro-optical crystal[J]. Optoelectronics Technology, 2015, 35(2): 101. DOI:10.3969/j.issn.1005-488X.2015.02.007 |
| [5] |
何启浩. 矩阵光学中的琼斯矩阵方法与其在偏振光中的应用[J]. 西南民族大学学报(自然科学版), 2014, 40(5): 772. HE Qihao. Method of Jones matrix of matrix optics and its application in polarized light[J]. Journal of Southwest University(Natural Science Edition), 2014, 40(5): 772. |
| [6] |
MARQUEZ A, CAMPOS J, YZUEL M J, et al. Characterization of edge effects in twisted nematic liquid crystal displays[J]. Optical Engineering, 2000, 39(12): 3301. |
| [7] |
YAMAUCHI M. Jones-matrix models for twisted-nematic liquid-crystal devices[J]. Applied Optics, 2005, 44(21): 4484. |
| [8] |
肖智宏.不均匀磁场磁致旋光效应及其电流传感技术研究[D].哈尔滨: 哈尔滨工业大学, 2017 XIAO Zhihong. Theoretic research on magneto optical rotation effect in inhomogeneous magnetic field and application to optical current sensing technology[D]. Harbin: Harbin Institute of Technology, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10213-1018897660.htm |
| [9] |
张国庆.光学电流互感器理论与实用化研究[D].哈尔滨: 哈尔滨工业大学, 2005 ZHANG Guoqing. Research on theory and practicality of optical current transformer[D]. Harbin: Harbin Institute of Technology, 2005 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y695126 |
| [10] |
程嵩.线性双折射对全光纤电流互感器传感特性影响的研究[D].哈尔滨: 哈尔滨工业大学, 2016 CHENG Song. The effect of linear birefringence on sensing characteristics of fiber optic current transformer[D]. Harbin: Harbin Institute of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10213-1016739359.htm |
| [11] |
JONES R C. A new calculus for the treatment of optical systems. VI. Experimental determination of the matrix[J]. Journal of the Optical Society of America, 1947, 37(2): 110. |
 2019, Vol. 51
2019, Vol. 51


