随着航班量的迅猛增长以及国内主要机场空域容量的日趋饱和,航空运输需求与运输系统供给之间的矛盾愈加突出,航班延误导致的问题越发严重.民航局公布的导致航班延误的原因中除了流量控制、恶劣天气外,航空公司生产计划编制不合理是第三大因素[1],因此如何制定高效的航班计划以最大程度减少航班延误成为民航管理当局和航空运输企业关注的焦点.
目前航班计划的研究集中在改进航班计划的设计方法以提高航班正点率,或是航班计划执行后,根据实际运行数据从经济角度进行航班计划评价.国外航空运输系统的计算机仿真技术已经日渐成熟,主要应用在机场系统,如Airfield Capacity Model、Approximate Network Delays、SIMAIR[2]和TAAM等,用于分析常见跑道构形的小时极限容量、航线网上旅客需求和机场容量等参数变化对飞行延误的影响、天气和机械故障等外界因素扰动下航班的表现、空域结构和滑行线路等对系统容量的影响.国内已有文献主要研究飞机起降之间的关联性,建立机场仿真优化模型[3]和基于Petri网构建多跑道冲突解脱模型[4]等.这些研究主要集中在单个机场跑道、滑行道、停机坪等空侧区及旅客进离港流程[5],对于机场群、航线网络、航班计划方面的系统级仿真研究较少.本文借鉴国内外现有仿真系统的技术方法,利用分类参数拟合法估计产生不同机型、不同机场等不同类别的航班运行各个阶段的随机运行参数,利用公式计算或者参考现实要求得到非随机运行参数,实现真实随机扰动环境下航班计划在航线网络层面的仿真.
1 航班计划运行流程分析与运行参数分类拟合 1.1 航班计划运行流程分析航班计划中,一架飞机会连续执行多个航班,每个航班分为起飞/降落、滑入/滑出、过站保障和航段飞行4个部分[6],如图 1所示.

|
图 1 航班运行流程图 Fig. 1 Flow chart of flight operation |
仿真模型的建立伴随各种参数的设定,参数精度决定了仿真效果.模型拟合所用数据为某大型航空公司2013—2016年的航班运行数据.不同机型、不同机场等不同类别的航班运行各个阶段,运行参数有着较大的区别,故采用分类参数拟合方法,实现模拟真实随机扰动环境下航班各个阶段的运行时间.将图 1的航班运行中过站阶段、起飞/降落与滑入/滑出阶段的运行参数按照影响因素分类拟合,分类类型如图 2所示.每一类别都是影响因素,将各种因素综合考虑来拟合运行参数,具体如下.

|
图 2 航班运行时间参数的分类 Fig. 2 Classification of flight time parameters |
1) 过站.不同机型飞机载客、载货量不等,不同规模机场(依据跑道数量及吞吐量划分)保障能力各异,这些因素都会对过站时间产生影响,对不同机型在不同规模机场的过站时间拟合来得到分布.一般来说过站时间符合Logistic分布,其累计分布曲线方程为
| $ N = \frac{C}{{1 + {{\rm{e}}^{a - rt}}}}. $ | (1) |
式中:N为过站时间;t为时间序列;C控制曲线最高点(peak point),C>0;a决定水平位置或移动点(takeoff point),a>0;r控制曲线陡度(gradient),r>0.
参数C用三点法估计.转换式(1)得到
| $ \ln \frac{{C - N}}{N} = a - rt. $ | (2) |
将历史数据序列的始点(t1, N1)、中点(t2, N2)、末点(t3, N3)分别代入上式,其中2t2=t1+t3,得到C值公式为
| $ C = \frac{{2{N_1}{N_2}{N_3} - N_2^2\left( {{N_1} + {N_3}} \right)}}{{{N_1}{N_3} - N_2^2}}. $ | (3) |
在此基础上,采用线性回归方法估计a、r两个参数.令y=ln(C-N)/N,将式(2)变换为线性式y=a-rt,用最小二乘法求出参数a、r的估计值,即
| $ a = \ln \left[ {\left( {C - {N_1}} \right)/{N_1}} \right], $ | (4) |
| $ r = \frac{{2\log \left[ {\left( {C - {N_2}} \right)/\left( {{e^a}{N_2}} \right)} \right]}}{{{t_1} - {t_3}}}. $ | (5) |
拟合优度检验(A-D和K-S检验)在列出的各个显著水平下都不拒绝此分布,则Logistic分布可以接受.
2) 起飞/降落.跑道上起飞/降落时间由跑道参数和飞机性能共同决定,采取根据跑道数n、容量c、长度l以及机型滑跑速度v估算跑道服务速率μ=ncl/v的方式来确定,是非随机运行参数;
3) 滑入/滑出.滑入/滑出时间依赖于机场结构特点,不同机场滑行道复杂程度差别较大所需时间也不一样[3].依据空侧构型、机场等级(表征滑行路线复杂度)、标准地面滑出时间规定对历史数据进行分类拟合,并考虑到机场繁忙程度对滑行时间的影响,统计枢纽机场一天内不同时间段的起降排队飞机数量得到“滑行时间-起降架次”函数,对高低峰的滑行时间进行修正,从而确定起飞/降落时间参数.
4) 航段飞行.考虑空中交通流量和天气的随机性,同一个OD对的飞行时间不固定.采用各航线的历史数据求均值,并按正态分布产生随机数进行模拟.
2 航班运行系统的模型建立航班计划运行模型是由多子系统组成的复杂系统,仿真时在不影响模拟效果的情况下,可对非关键环节适当简化.将模型分为图 1所示的起飞/降落、滑入/滑出、过站保障、航段飞行4个功能模块;设置对象为飞机发生器、降落滑入、过站、补充过站、滑出起飞、航段飞行;并设置临时实体为飞机.仿真流程如图 3所示,航班每次开始或结束一个功能模块都是根据时间拟合参数产生的相应随机数或者计算得到的参数模拟各种动作.
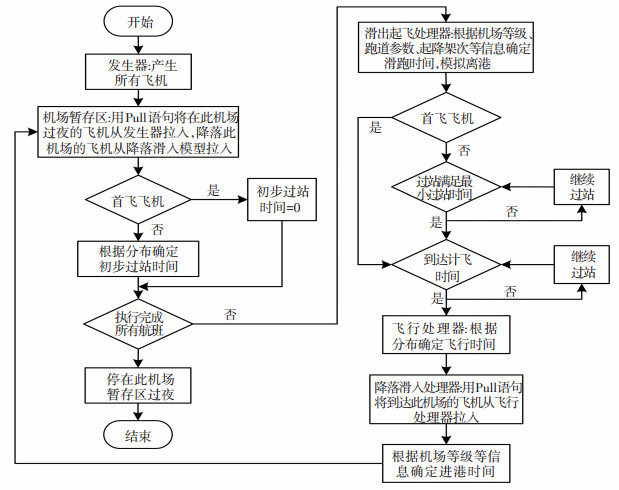
|
图 3 仿真流程图 Fig. 3 Simulation flow chart |
输入输出层主要将仿真系统和航班计划的基础数据进行对接,设置仿真运行结果数据显示界面.系统输入信息包含:航班计划表(航班号、机号、机型、起飞/降落站、计划起飞时间)、机场信息表(各机场代码、名称、规模及跑道参数)、最小过站时间表、航段飞行时间表、机场等级表及枢纽机场起降架次表.系统输出信息主要包括到达时间、滑入结束时间、初步过站结束时间、滑出结束时间、起飞时间等.
2.2 过站保障模块过站保障因其任务流程复杂、参与人员较多、受机场能力限制的特征,成为导致延误的重要环节之一.仿真模型中用发生器、暂存区两个对象模拟过站保障,具体建模步骤为
步骤1 发生器生成飞机并记录首个航班信息.
1) let M =飞机数,N =航班数;
2) for(j=1,j<=M,j++)
for(i=1,i<=N,i++)
If(i=第j架飞机首个航班)
由航班计划在j飞机标签上记录航班信息.
步骤2 设置暂存区标签信息并模拟初步过站.
1) let K =机场数,飞行次数初始值=0;
for(k=1,k<=K,k++)
设置K个暂存区(停机位)机场信息标签;
2) for(k=1,k<=K,k++)
for(j=1,j<=M,j++)
{if(j飞机起飞机场代码=k停机位机场代码)
设置pull条件,使得在此机场过夜以及进港滑行完毕的j飞机进入k停机位;
if(j飞机已执行完航班串所有航班)
将其留在此机场过夜;
else
{记录j飞机下一航班信息;
确定航班相应的过站分布,产生随机时间t以模拟初步过站(首飞航班t为0);
通过senddelaymessage命令设置消息延迟,使得消息延迟时间t后到达消息触发器,并与优先级设置相结合实现初步过站.
}
}
2.3 起飞/降落与滑入/滑出模块起飞/降落是指飞机起飞、着陆时在跑道上运行的过程,滑入/滑出是指飞机从跑道滑到停机坪,使已着陆的飞机迅速离开跑道,或从停机坪到跑道的过程.跑道数目、几何构型、通信导航辅助设备等因素会影响这些过程的时间大小.此模块对象为处理器,建立模型步骤为
步骤1 for(k=1,k<=K,k++)
对代表降落滑入、滑出起飞的2K个处理器设置机场代码、机场等级、跑道参数.
步骤2 if(j飞机起飞机场=k降落滑入处理器机场)
设置处理器的pull条件,使目的地为此机场的飞机从飞行模块进入到此处理器.
步骤3 由处理器标签机场等级、跑道参数结合枢纽机场起降架次表确定进离港滑跑时间.
2.4 补充过站模块由于滑跑时间是分布产生的随机数,而计划起飞时间固定,为保证航班不因随机的滑跑时间导致起飞延误或提前,在滑行道滑出、跑道起飞后引入虚拟模块“补充过站”进行调节.补充过站用暂存区模拟,仿真步骤为
步骤1 根据机型和机场规模确定最小过站时间;
步骤2 let t1=初步过站时间,t2=最小过站时间;
if(t1<t2)增加过站时间Δt=t2-t1;
else增加过站时间Δt=0.
步骤3 let T1=离港滑跑结束时刻,T2=计划起飞时间;
If(T1+Δt<=T2)在T2时刻起飞;
else在T1+Δt时刻起飞.
步骤4 通过senddelaymessage命令实现补充过站.
2.5 航段飞行模块航段飞行指飞机起飞脱离地面以阶梯式或固定角度爬升,到达预定高度后保持水平等速飞行状态巡航,临近目的地机场空域时逐渐减少速度下降准备进近着陆的过程.此模块是以处理器为对象建立的,步骤为
步骤1 根据航班计划表的起飞、目的机场得到飞行时间的正态分布,产生随机数仿真.
步骤2 更新飞行次数=飞行次数+1.
3 航班运行系统模型的检验和仿真分析 3.1 航班运行系统模型的检验为检验开发的Flexsim航班运行系统模型,使用某大型航空公司有效数据,选择2016年较繁忙的5—10月份每月1号为校验日,核实及校正仿真模型.检验指标包括起飞航班正点率、起飞延误时间、到达航班正点率、到达延误时间、飞机利用率、过站时间[7-8].经反复调试校正,仿真结果与实际运行误差见表 1,对误差进行统计分析见表 2、3.误差值均较小,其中起飞/到达平均延误时间误差的平均值为-3~4 min,最大偏差为-6~6 min, 各指标平均误差比为-0.02~0.04,最大偏差比在-0.08~0.08之间,较为合理.说明仿真系统可以较好地模拟航空公司航班计划的实际运行状况,能够为航班计划研究提供可靠、高效的系统平台.
| 表 1 仿真结果与实际运行误差 Tab. 1 Error between simulation results and actual operation statistics |
| 表 2 仿真结果误差分析 Tab. 2 Error analysis of simulation results |
| 表 3 仿真结果误差比值分析 Tab. 3 Error ratio analysis of simulation results |
以大型航空公司某一繁忙日航班计划为实例进行仿真及分析.当日航班计划调配130架飞机、15种机型,包括483个国内定期旅客航班,83个国内机场,以PVG为运营基地,建立仿真模型如图 4所示(为保证模型对航班计划的通用性,建立的模型包括118个国内主要机场).

|
图 4 航班运行系统仿真模型 Fig. 4 Simulation model of flight operation system |
为探究时间参数对航班计划运行的影响,将航班在各阶段所用的时间分别设置为固定常量和随机参数两种情况进行分析.
1) 固定时间参数.航班各时间参数为此繁忙日所在月的均值.其中过站时间按不同机型在不同吞吐量规模机场、起飞/降落与滑入/滑出按不同等级机场、飞行时间按各航线分别求均值.对航班计划进行仿真,执行航班数最多的8个机型各项运行指标见表 4.时间参数取平均值时,各机型航班平均过站时间、平均轮档时间、飞机日利用率的航班计划数据与仿真结果数据差值较小,差值比均大于-5%,计划预留时间较多.平均缓冲时隙较为充裕,离港和到港正常率较高,说明航班计划在模拟的运行环境中具有很好的可行性.
| 表 4 固定时间参数的仿真运行指标 Tab. 4 Simulation operation indicators with fixed time parameters |
2) 随机时间参数.虽然航班计划在时间参数为常量时运行效率较高,但在实际执行中机场保障、机场航班量等各种影响因素使得运行时间产生波动,考虑在随机时间参数下的航班计划运行更具实际意义.将航班在各阶段运行时间设为历史数据拟合得到的分布或计算得到的参数,仿真结果见表 5.
| 表 5 随机时间参数的仿真运行指标 Tab. 5 Simulation operation indicators with random time parameters |
各机型平均过站时间差值为负,且差值比大多小于-8%,说明航班计划过站时间的制定普遍偏小,不能满足实际运行所需保障时间,导致离港航班正常率较低,其中A321的平均过站时间差值比最小,为-14.00%,离港航班正常率只有71.43%;飞机日利用率差值为正,则航班计划预留的飞行时间较大,到港航班正常率也相应提高,其中A325的飞机日利用率差值比最大,为12.83%,航班到港正常率高达91.30%;平均轮档时间差值比较小,在-6%~4%之间,说明飞机从撤轮档滑出停机位到滑入停机位上轮档的计划时间与实际运行时间相似,故影响航班正常率的主要因素不在此过程中,而在于过站保障环节.平均缓冲时隙的设计可以吸收上一个航段产生的牵连延误[9-10],由于A321的缓冲时隙仅2.22 min,在拥挤的机场高峰时段易产生延误,导致离港航班正常率偏低.综上,该航空公司在编制航班计划时应适当增加过站保障时间,以提高正常率.
3.3 流控下航班运行仿真分析预测航班在突发状况下的受扰程度、评价航班计划的抗干扰能力、检验航班计划的鲁棒性可以增强管理者对突发事件的掌控和处理能力[11].以流控这一突发扰动为例,对不正常航班进行仿真模拟,分析其对延误的影响.
对流控的具体情况作如下假设:厦门机场在上午10点到下午4点之间流控,所有在这个时间段内从厦门机场起飞、到达厦门机场的航班,ATC将重新给它们分配一个计划起飞时间,此计飞比原计飞晚30~180 min(随机分布).仿真结果显示航空公司共有9条航班串受影响,以1813和2220号飞机执行的两条航班串为例,仿真输出数据如图 5所示(纵坐标差值=流控仿真数据-正常仿真数据),其中带*标注的为流控时间段内在厦门机场起降的直接受影响航班.
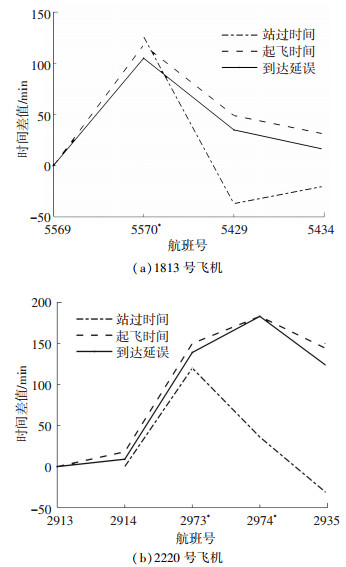
|
图 5 流控与正常情况下的仿真结果差值 Fig. 5 Differences between simulation results under flow control and normal condition |
分析上图可知,1813号飞机在首个航班5569时处于正常状态,无须过站,无起飞和到达延误.在执行经厦门的5570航班时遭遇流控,起飞和到达延误与正常相比分别增大118、105 min,同时由于起飞受限过站时间增加126 min.继续执行后续的5429和5434航班时受到波及影响,仍有较大起飞、到达延误,但由于设置了缓冲时隙,延误逐站减小,最终差值分别为31、16 min,过站时间则由于缓冲时隙的存在而被压缩,比平时分别少了37、20 min. 2220号飞机与1813号飞机类似,但因有两个航班连续遭遇流控,导致延误进一步增加.
研究结果表明,流控不仅对遭受流控的航班有直接影响,还会对与其在同一个航班串上的后续航班产生牵连影响. 6 h的流控虽影响了在厦门机场起降的9个航班,却波及了其后的28个航班,产生严重后果.它导致受直接影响的航班过站时间大幅增加,而受牵连影响的航班过站时间减少,小于正常过站时间.所有受扰航班均产生很大的起飞和到达延误,延误时间沿航班串向下传递,且由于设置了缓冲时隙,呈现下降趋势.但延误最后并没有完全被缓冲时隙吸收,编排航班计划时应适当增大缓冲时隙,以应对不正常情况.
4 结论1) 面向航空运输业持续高速发展、机场和空域等资源紧缺、航班延误严重的现实问题展开研究,通过模拟起飞/降落、滑入/滑出、过站保障、航段飞行等真实的航班执行过程,建立了含有118个国内主要机场的航班运行仿真模型,在Flexsim平台上予以实现,并以某大型航空公司的运行数据验证了模型的有效性.
2) 利用该仿真模型可以输出延误时间、飞机利用率等指标, 对航班计划进行评估,从而找到影响航班运行的瓶颈因素;可以提前预测航班出现异动的概率,及时作出调整,控制航班的不正常水平.
3) 模型可以加入流控、天气等外部扰动形成不正常航班,探究延误的传播特性,并对航班计划的鲁棒性、稳定性进行分析和优化.
4) 模型虽然仅包括国内118个机场,但有较好的延展性,只要有足够的数据支持,可以建立包含国内、国际航班的完整的航班运行仿真系统.对于航班计划的编制、运行方案的制定有一定的指导意义,可为实施航班的智能化管理提供理论依据.
| [1] |
史彦飞.基于旅客选择行为的航班计划优化研究[D].南京: 南京航空航天大学, 2012 SHI Yanfei. Research on airline schedule optimization based on passenger choice behavior[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10287-1012042213.htm |
| [2] |
LEE L H. A multi-objective genetic algorithm for robust flight scheduling using simulation[J]. European Journal of Operational Research, 2007, 177(3): 1948. DOI:10.1016/j.ejor.2005.12.014 |
| [3] |
马正平, 崔德光. 机场航班延误优化模型[J]. 清华大学学报(自然科学版), 2004, 44(4): 444. MA Zhengping, CUI Deguang. Optimizing airport flight delays[J]. Journal of Tsinghua University (Science and Technology), 2004, 44(4): 444. |
| [4] |
王琪.复杂机场多跑道运行调度方案评估研究[D].南京: 南京航空航天大学, 2016 WANG Qi. Evaluation of multi-runway operation scheduling scheme for complex airport[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10287-1016791256.htm |
| [5] |
陆迅, 唐小卫, 朱金福. 航站楼旅客离港流程仿真研究[J]. 西南交通大学学报, 2009, 44(1): 135. LU Xun, TANG Xiaowei, ZHU Jinfu. Simulationanalysis of passenger departure procedure in airport terminals[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 135. DOI:10.3969/j.issn.0258-2724.2009.01.025 |
| [6] |
上官雪民.航班计划的模拟与优化研究[D].上海: 复旦大学, 2008 SHANGGUAN Xuemin. Optimization on flight schedule simulation[D]. Shanghai: Fudan University, 2008 |
| [7] |
吴薇薇. 基于机场延误预测的航班计划优化研究[J]. 交通运输系统工程与信息, 2016, 16(6): 189. WU Weiwei. Flightplan optimization based on airport delay prediction[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(6): 189. DOI:10.3969/j.issn.1009-6744.2016.06.029 |
| [8] |
STOJKOVIC G. An optimization model for a real-time flight scheduling problem[J]. Transportation Research Part A Policy and Practice, 2002, 36(9): 779. DOI:10.1016/S0965-8564(01)00039-8 |
| [9] |
LAN Shan. Planning forrobust airline operations: optimizing aircraft routings and flight departure times to minimize passenger disruptions[J]. Transportation Science, 2006, 40(1): 15. DOI:10.1287/trsc.1050.0134 |
| [10] |
TANG C H. An integrated model and solution algorithms for passenger, cargo, and combi flight scheduling[J]. Transportation Research Part E, 2008, 44(6): 1004. DOI:10.1016/j.tre.2008.02.002 |
| [11] |
YAN Shangyao. Asimulation framework for evaluating airline temporary schedule adjustments following incidents[J]. Transportation Planning and Technology, 2005, 28(3): 189. DOI:10.1080/03081060500120324 |
 2019, Vol. 51
2019, Vol. 51


