2. 北京交通大学 交通运输学院, 北京 100044
2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
城市轨道交通运营系统是一个统一的整体,列车运行计划是城市轨道交通系统的综合性计划和产品,各运营线路列车时刻表的协调优化,对于提高城市轨道交通网络的效率、稳定性和安全性、提升城市轨道交通服务水平和乘客满意度,具有重要的理论和现实意义.为保障网络换乘节点的换乘效率,计划编制人员需协调网络中各线路在换乘站的到发时刻,来保证换乘乘客的最大平滑换乘,即网络换乘协同优化问题.
实际上,网络换乘协同优化是一个十分困难却又十分重要的计划编制任务.目前,已有大量研究学者对此展开研究.文献[1-2]定义协同为车辆同时到达,并以最大化同时到达车辆数为目标构建了最大化换乘协同优化模型,并设计启发式算法求解.文献[3]引入时间窗扩展了协同的定义,定义在衔接时间窗内同时到达即为协同,并设计了启发式算法求解.文献[4]则是通过引入0、1变量来刻画换乘等待时间,并以最小化总乘客换乘等待时间为目标构建换乘协同优化模型.文献[5-6]采用多目标规划方法构建换乘协同优化模型.由于以上模型中存在大量0、1变量,模型求解困难,众多研究学者针对换乘协同优化模型求解算法展开研究.文献[7-11]针对换乘协同优化模型,设计了多点迭代、领域搜索、禁忌搜索等局部优化算法.文献[12]根据0、1变量的分布特征及其与发车间隔的关系,构建有效不等式,以提高分支定界算法的剪枝效率,加快求解速度.文献[13]考虑列车可行的发车时间、到站时间和协同到达时间窗,删除不可能协同到达的决策变量和约束,来缩减了问题的求解空间,提高模型求解效率.文献[14-15]提出了基于等间隔平行运行图的换乘协同优化模型,通过固定各运营线路的发车间隔,以研究时段内各线路首列车发车时刻为变量构建优化模型.
总的来说,文献[1-13]换乘协同优化模型灵活性高,但是模型0、1变量多,求解难度大,提出的求解算法和加速策略仍不能满足实际大规模网络的求解需求,且由于优化模型中列车发车时刻过于灵活,运用智能算法,如遗传算法,解的更新过程中会产生大量不可行解,存在根本性困难;而文献[14-15]规定列车按照等间隔发车,有效降低了模型的变量规模,求解效率高,能快速生成网络换乘协同方案,但该方法只局限于等间隔发车模式.本文在等间隔发车的基础上引入列车发车相位,同时引入发车时刻的柔性偏移量来解决等间隔发车灵活性差的问题,并考虑其对换乘乘客分布的影响,以最大化网络总换乘协同乘客数为目标,构建基于柔性发车间隔的城市轨道交通时刻表协同优化模型;并以各线路的列车发车相位以及柔性偏移量为染色体设计了遗传算法.该方法巧妙保留了等间隔发车的求解优势,克服了高灵活性下解更新困难的问题.最后,利用小规模网络算例与精确算法对比分析确认遗传算法性能,以北京市轨道交通网络展开大规模实例研究.
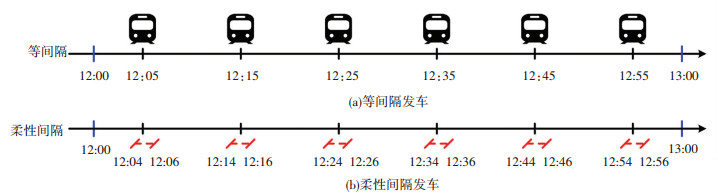
1 基于柔性发车间隔的时刻表协同优化模型目前,在城市轨道交通实际运营中,为充分考虑高峰和非高峰时段客流的差异,通常将运营日划分为若干个时段,每个时段的列车按照等间隔均衡发车的方式运行,如图 1(a)所示.实际上,为提高城市轨道交通系统的服务水平,运营管理者可在等间隔发车的基础上对列车的发车时刻进行柔性调整,以更好地匹配乘客需求,如图 1(b)所示.图中,运营时段为12:00—13:00,平均发车间隔为10 min,等间隔发车情况下首列车发车时刻为12:05,发车间隔柔性阈值为1 min.
|
图 1 两种发车策略示例 Fig. 1 Two kinds of departing schemes |
等间隔发车策略是目前城市轨道交通运营管理中常用的时刻表制定策略,这种方式易于管理,但是在匹配客流需求方面具有一定的局限性.柔性间隔发车策略的内涵是在刚性控制的等间隔发车的前提下,确定各列车发车时刻的基准点,同时允许列车发车时刻可根据需求在基准点附近柔性调整一定范围,刚柔结合,增强了时刻表制定策略的灵活性.
1.1 模型假设和模型参数模型假设如下:1)乘客换乘走行时间为定值,不考虑不同人群间换乘走行时间的差异及其波动的影响. 2)乘客路径选择行为是已知且固定的,且不会受时刻表微调的影响;3)基于平峰时段进行时刻表协同优化建模,列车载客能力充足,不存在乘客滞留现象.
定义模型相关参数如下:I为分方向线路(简称线路)集合,I={i, i′| i, i′=1, 2, …, n};Ti为线路i的列车集合,Ti={t, t′| t, t′=1, 2, …, ki};Si为线路i的车站集合,Si={s, s′| s, s′=1, 2, …, mi};X为换乘弧集合,X={x| x= i, s → i′, s′},其中,i, s → i′, s′表示乘客可经由线路i的车站s换乘至线路i′的车站s′;ustart为研究时段的开始时间;hi, λi分别为线路i的平均发车间隔和柔性偏移阈值,其中柔性偏移阈值与平均发车间隔相关;rsi, t为线路i的车次t从车站s-1至车站s的区间运行时间;zsi, t为线路i的车次t在车站s的停站时间;wx, bx分别为换乘弧x的换乘走行时间和可容忍的协同等待时间;px为换乘弧x的平均换乘乘客数.
同时,定义模型相关变量如下:Φi为线路i的在等间隔发车模式下的列车发车相位;Ei, t为线路i的车次t的发车时刻柔性偏移;Dsi, t为线路i的车次t离开车站s的时刻;Asi, t为线路i的车次t到达车站s的时刻;Yxt, t′为线路i的车次t经由换乘弧x换乘至线路i′的车次t′的换乘协同索引;Pxt为线路i的车次t经由换乘弧x换乘至线路i′的换乘乘客数;Oxt, t′为线路i的车次t经由换乘弧x换乘至线路i′的车次t′的换乘协同乘客数.
1.2 模型约束1) 柔性发车间隔.柔性间隔发车时刻表主要取决于两个因素:一是刚性控制.为保证时段内发车频率的要求,等间隔发车情况下首列车在首站的发车时刻与研究时段的开始时刻之差,简称为列车发车相位,应为非负值且不得大于该线路的平均发车间隔.二是柔性调整.柔性间隔发车与等间隔发车情况下列车在首站的发车时刻之差,简称为柔性偏移量,其绝对值应不得大于发车刻前后可调整的最大范围,即柔性偏移阈值.列车发车相位决定了列车发车时刻柔性调整的基准点,柔性偏移阈值控制了列车发车时刻在其基准点附近的最大柔性调整幅度.柔性间隔发车下刚性控制和柔性调整约束可以分别描述为
| $ {{u_{{\rm{stat }}}} \le |{\mathit{\Phi }^i} \le {u_{{\rm{stant }}}} + {h^i}} $ | (1) |
| $ { - {\lambda ^i} \le {E^{i,t}} = D_1^{i,t} - {\mathit{\Phi }^i} - (t - 1) \times {h^i} \le {\lambda ^i}} $ | (2) |
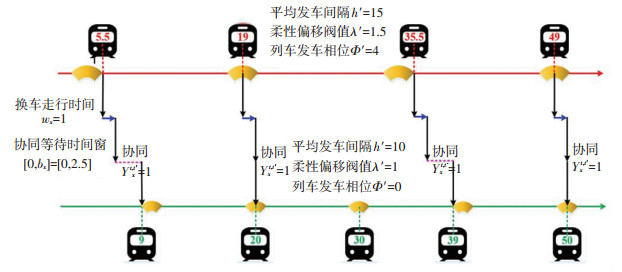
2) 换乘协同索引和换乘协同乘客数.在等间隔发车情况下,协调两线路的列车发车相位可提高在换乘节点的换乘效率,但该方式灵活性较低,最大可实现协同的换乘关系数少;当线路i的发车间隔为线路i′的正整数倍时,可实现所有换乘关系协同,否则难以保证所有换乘关系同时实现协同.而在柔性间隔发车情况下,同时协调两线路的列车发车相位和各列车发车时刻的柔性偏移量,可有效提高换乘协同乘客数. 图 2为柔性间隔发车情况下的时刻表协同方案示例,其中平均发车间隔hi=15, hi′=10,柔性偏移阈值λi=1.5, λi′=1;在等间隔发车情况下,线路i上每小时最多两列车的乘客可实现协同换乘;而在柔性间隔发车情况下,乘客换乘走行到达线路i′的站台后,线路i′的列车均能在协同等待时间窗0, bx = 0, 2.5内到达,即所有换乘关系能同时实现协同,换乘效率高.
|
图 2 柔性间隔发车情况下的时刻表协同方案(min) Fig. 2 Synchronized timetables in flexible departing cases (min) |
因此,为描述换乘弧x各列车间是否实现协同,引入0、1变量Yxt, t′,若乘客经由线路i的车次t换乘至线路i′的车次t′的等待时间在协同时间窗[0, bx]内,其值为1,否则为0.其含义通过协同关系不等式描述为
| $ \begin{array}{*{20}{c}} { - M \times \left( {1 - Y_x^{t,{t^\prime }}} \right) \le D_{{s^\prime }}^{{i^\prime },{t^\prime }} - \left( {A_s^{i,t} + {w_x}} \right) \le }\\ {{b_x} + M \times \left( {1 - Y_x^{t,{t^\prime }}} \right),} \end{array} $ | (3) |
式中M为一个足够大的正整数.
为更准确的刻画换乘衔接关系,本文考虑研究时段内各列车的换乘乘客数与列车载客量成比例相关,即从线路i的车次t经由换乘弧x换乘至线路i′的换乘乘客数Pxt与车次t的载客量相关.在这里,本文假设列车载客量主要取决于列车间的发车间隔,因此换乘乘客数可以表示为
| $ P_x^t = {p_x} + \left( {D_s^{i,t} - D_s^{i,t - 1} - {h^i}} \right) \times {p_x}/{h^i}, $ | (4) |
然后结合式(3),可计算换乘协同乘客数,计算公式为
| $ O_x^{t,{t^\prime }} = P_x^t \times Y_x^{t,{t^\prime }}. $ | (5) |
式中px/hi为灵活发车间隔下单位时间内的换乘乘客数.
3) 列车运行约束.列车运行过程为出发、区间运行、到达和停留的周期交替过程,为保证这些过程的接续,需保证列车离站时刻为列车到站时刻和在该站的停站时间之和,且列车到站时刻为在首站发车时刻和前行车站区间运行时间和停站时间之和.列车运行约束可以描述为
| $ {D_s^{i,t} = A_s^{i,t} + z_s^{i,t},} $ | (6) |
| $ {A_s^{i,t} = D_1^{i,t} + \sum\limits_{k = 1}^s {r_k^{i,t}} + \sum\limits_{k = 1}^{s - 1} {z_k^{i,t}.} } $ | (7) |
本文以网络总换乘协同乘客数最大化为目标,构建柔性发车间隔的时刻表协同优化模型,目标函数可以描述为
| $ \max \sum\limits_{x \in X} {\sum\limits_{t \in {T_i}{t^\prime } \in {T_{{i^\prime }}}} {O_x^{t,{t^\prime }}} } . $ | (8) |
根据式(5)可知,换乘协同乘客数为换乘协同索引和换乘乘客数两变量的乘积,为非线性约束.因此,为便于模型求解,式(5)可以线性化处理为
| $ P_x^t \le O_x^{t,{t^\prime }} + M \times \left( {1 - Y_x^{t,{t^\prime }}} \right), $ | (9) |
| $ 0 \le O_x^{t,{t^\prime }} + M \times Y_x^{t,{t^\prime }}. $ | (10) |
模型转换后为混合整数线性规划模型,可采用线性规划软件(如Cplex, Gurobi, Yalmip)直接求解.然而,优化模型中存在大量0、1变量,随着线路数目及换乘车站数目增多,决策变量剧增,求解效率将成为该类模型的一大难题.因此,本文设计遗传(GA)算法,来快速高效求解优化模型.
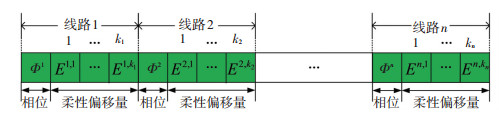
2 遗传算法 2.1 遗传算法流程本文以各线路在等间隔发车模式下的相位以及各列车的发车时刻柔性偏移量作为基因组成染色体,具体表示形式如图 3所示.
|
图 3 染色体表现形式 Fig. 3 Form of chromosome |
遗传算法的终止准则一般有3种:1)最优解在一定迭代次数后不再改变;2)种群中最优解和最差解的差值小于给定的差值;3)迭代次数达到设定的最大迭代次数.本文选择第3种方法作为算法的终止准则,具体算法流程如下.
步骤1 初始化.1)设置初始的遗传算法参数:种群规模J,初始遗传代数q=0,最大遗传代数Q,交叉概率px,变异概率pm;2)输入初始数据,生成初始种群P(q),并计算每一个个体的目标函数值O(j).
步骤2 选择、交叉和变异.1)计算每个个体的适应度值
步骤3 判断算法是否终止.1)更新算法遗传代数q=q+1;2)如果q=Q,算法终止,记录最优的个体编号和目标函数值,否则返回步骤2.
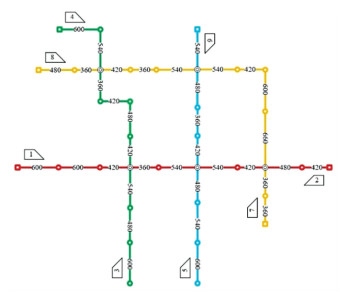
2.2 算例分析本文设计一个包含4条双线运营线路(8条单向运输线路)、5座换乘站的算例网络,通过比较精确算法和遗传算法的优化效果,来检验遗传算法的性能.优化模型为混合整数线性规划模型,包含992个0、1变量,在C#编程环境下调用Cplex混合整数规划求解器的分支割平面(Branch-and-Cut, B & C)算法并编译遗传算法来求解,求解结果见表 1.算例网络拓扑结构如图 4所示,其中发车时段为60 min,线路1、2平均发车间隔为10 min,线路3、4、5、6为12 min,线路7、8为15 min;总列车数为40列,乘客可容忍的协同等待时间设为3 min.
| 表 1 B & C算法和GA算法求解结果 Tab. 1 Optimized results of B & C algorithm and GA algorithm |
|
图 4 算例网络拓扑结构图 Fig. 4 Topology of the example network |
表 1中柔性系数为柔性偏移阈值与平均发车间隔之比.由表可见,B & C在等间隔发车策略下,能快速生成最优解;而引入部分柔性后,最优换乘协同时刻表的求解时间急剧增长,精确算法不能满足大规模实际网络的求解需求,而遗传算法均能快速生成优化方案.此外,比较精确算法和遗传算法优化目标值可见,遗传算法求得的优化解质量高,其与最优解的相对误差不大于10%,在可接受的范围内,遗传算法的求解性能好,可应用于大规模实例网络的换乘协同时刻表生成.
3 实例研究 3.1 实例描述本文以2017年6月北京市轨道交通网络作为案例对象,来验证方法求解大规模实际网络的效果.除机场线外,北京市轨道交通网络包含18条双向运营线路,53座换乘站,372个换乘弧,网络拓扑结构如图 5所示.

|
图 5 北京市轨道交通网络拓扑图 Fig. 5 Topology of the Beijing urban rail transit network |
研究时段选取为某工作日的平峰时段12:00—13:00,区间运行时间以及停站时间等根据实际列车运行图确定,换乘站乘客的平均换乘走行时间通过实际调查获得,研究时段内各换乘弧的换乘客流量根据票款清分结果得到.此外,1、2、4、5、6、7、8、9、10号线的平均发车间隔分别为240、270、240、270、360、360、420、330、270 s,13、14、15、16号线的平均发车间隔分别为360、480、660、480 s,八通线、昌平线、亦庄线、房山线的平均发车间隔分别为390、630、660、480 s.此外,发车柔性偏移阈值与该线路平均发车间隔相关.
3.2 优化效果分析在Inter Pentium CPU G3240 3.1 GHz,4 GB RAM的电脑上,在C#编程环境下生成数据文件和模型文件,模型包含5万多个0、1变量,精确求解困难;编译遗传算法来求解优化模型.此外,由于不同的参数设置对遗传算法性能有较大影响,因此,测试了不同参数组合下的优化效果,最终选择遗传算法交叉概率px为0.85,变异概率pm为0.15,种群规模J为200,迭代最大遗传代数Q为300.
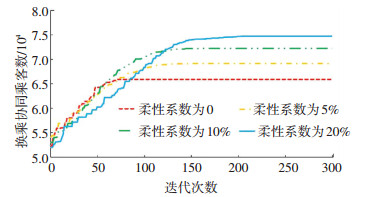
为分析柔性偏移阈值的变化对换乘协同优化效果的影响,本文设计了4种不同柔性系数下的换乘协同时刻表生成案例,其换乘协同乘客数和收敛时间见表 2,并绘制不同柔性系数下遗传算法的求解进程图,如图 6所示.其中,柔性系数为0的时刻表方案,实际上是等间隔发车情况下的换乘协同时刻表方案.
| 表 2 大规模实例网络的GA算法求解结果 Tab. 2 Optimized results of GA algorithm for the large-scale network |
|
图 6 不同柔性系数下遗传算法求解进程图 Fig. 6 Progress chart of GA algorithm for different levels of flexibility |
由图 6可知,等间隔发车模式下的时刻表实现换乘协同乘客数小,换乘乘客的平均换乘效率低,城市轨道交通系统的服务水平低.柔性系数0.10(0.05)的时刻表制定时引入少许柔性,实现换乘协同的乘客数较等间隔发车情况下的时刻表增长11.85%(6.54%),换乘效率得到显著提高.随着柔性系数的增大,时刻表的灵活性越高,实现换乘协同的乘客数也越多,但增长率下降,因此运营管理人员可生成多种柔性系数下换乘协同方案以比较优化效果,结合实际需求来确定最终柔性调整阈值.此外,算法迭代次数达到300次时不同柔性系数下优化结果均已收敛,求解时长不超过10 min,且柔性系数越高,遗传算法收敛越慢,迭代收敛代数越大;求解结果表明该方法能快速生成较高质量的网络换乘协同方案,能满足大规模实际城市轨道交通网络的求解需求.
4 结论1) 等间隔发车情况下通过协调两线路的列车发车相位提高换乘效率有限,适当容许列车的发车时刻可柔性调整一定范围,能有效提升实现换乘协同数.引入各线路在等间隔发车模式下的列车发车相位和列车发车时刻的柔性偏移量,同时考虑换乘乘客数目与换出线路列车间发车间隔的关系,构建了基于柔性发车间隔的时刻表协同优化模型.
2) 由于优化模型中存在大量0、1变量,模型求解困难,精确求解算法难以满足大规模实际网络的求解需求,以各线路在等间隔发车模式下的相位以及各列车的发车时刻柔性偏移量为染色体,设计了遗传算法,并通过设计小算例与精确算法求得最优解对比,分析确认了该方法能有效生成高质量的优化解.
3) 以北京市轨道交通网络为案例对象进行实证分析,案例分析结果表明在制定时刻表计划时引入一定的柔性,能有效提高换乘效率,提升城市轨道交通系统的服务水平,且随着柔性系数越大,换乘效率提高越不明显,运营管理人员可根据实际需求来设定柔性系数.
| [1] |
CEDER A, TAL O. Designing synchronization into bus timetables[J]. Journal of the Transportation Research Board, 2001, 1760(1): 28. |
| [2] |
CEDER A. Optimal multi-vehicle type transit timetabling and vehicle scheduling[J]. Procedia-Social and Behavioral Sciences, 2011, 20(6): 19. |
| [3] |
ERANKI A. A model to create bus timetables to attain maximum synchronization considering waiting times at transfer stops[D]. Hillsborough: University of South Florida, 2004
|
| [4] |
WONG C W, YUEN W Y, FUNG K W, et al. Optimizing timetable synchronization for rail mass transit[J]. Transportation Science, 2008, 42(1): 57. |
| [5] |
周艳芳, 周磊山, 乐逸祥. 城市轨道网络换乘站列车衔接同步协调优化研究[J]. 铁道学报, 2011, 33(3): 9. ZHOU Yanfang, ZHOU Leishan, YUE Yixiang. Synchronized and coordinated train connecting optimization for transfer stations of urban rail networks[J]. Journal of the China Railway Society, 2011, 33(3): 9. DOI:10.3969/j.issn.1001-8360.2011.03.002 |
| [6] |
KWAN C M, CHANG C S. Timetable synchronization of mass rapid transit system using multiobjective evolutionary approach[J]. IEEE Transactions on Systems Man and Cybernetics Part C, 2008, 38(5): 636. |
| [7] |
刘志刚, 申金升, 王海星, 等. 基于协同发车的区域公交时刻表生成模型研究[J]. 交通运输系统工程与信息, 2007, 7(2): 109. LIU Zhigang, SHEN Jinsheng, WANG Haixing, et al. Regional public transportation timetabling model with synchronization[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(2): 109. DOI:10.3969/j.issn.1009-6744.2007.02.019 |
| [8] |
IBARRA-ROJAS O J, RIOS-SOLIS Y A. Synchronization of bus timetabling[J]. Transportation Research Part B, 2012, 46(5): 599. |
| [9] |
IBARRA-ROJAS O J, LÓPEZ-IRARRAGORRI F, RIOS-SOLIS Y A. Multiperiod bus timetabling[J]. Transportation Science, 2016. |
| [10] |
罗孝羚, 蒋阳升. 基于公交数据挖掘的时刻表排班协同换乘优化[J]. 交通运输系统工程与信息, 2017, 17(5): 173. LUO Xiaoling, JIANG Yangsheng. Timetable transfer-coordination optimization based on transit data mining[J]. Journal of Transportation Systems Engineering and Information, 2017, 17(5): 173. |
| [11] |
GUO X, SUN H, WU J, et al. Multiperiod-based timetable optimization for metro transit networks[J]. Transportation Research Part B, 2017, 96: 46. |
| [12] |
FOUILHOUX P, IBARRA-ROJAS O J, KEDAD-SIDHOUM S, et al. Valid inequalities for the synchronization bus timetabling problem[J]. European Journal of Operational Research, 2016, 251(2): 442. |
| [13] |
吴影辉, 唐加福. 考虑不均匀发车间隔的公交网络时刻表优化模型[J]. 东北大学学报(自然科学版), 2016, 37(4): 461. WU Yinghui, TANG Jiafu. Optimization model for bus network timetabling with uneven headway[J]. Journal of Northeastern University (Natural Science), 2016, 37(4): 461. DOI:10.3969/j.issn.1005-3026.2016.04.002 |
| [14] |
SHAFAHI Y, KHANI A. A practical model for transfer optimization in a transit network: model formulations and solutions[J]. Transportation Research Part A, 2010, 44(6): 377. |
| [15] |
禹丹丹, 韩宝明, 董宝田, 等. 基于换乘协同的轨道交通网列车时刻表优化模型[J]. 中国铁道科学, 2015, 36(4): 129. YU Dandan, HAN Baoming, DONG Baotian, et al. Optimization model of train timetable for rail transit network based on transfer synchronization[J]. China Railway Science, 2015, 36(4): 129. DOI:10.3969/j.issn.1001-4632.2015.04.20 |
 2019, Vol. 51
2019, Vol. 51


