2. 浙江省机电产品质量检测所,杭州 310051
2. Zhejiang Testing & Inspection Institute for Mechanical and Electrical Products Quality, Hangzhou 310051, China
目前,国内外大部分学者在对关节轴承进行热分析时,将内外圈球面的摩擦副考虑为光滑接触.而在现实情况下,内外圈接触面是粗糙的,表面分布有很多微凸体.这些微凸体相互接触,接触面积总和即为实际接触面积,其远远小于名义接触面积,微凸体峰顶实际的接触压力通常大于光滑接触时的压力,会产生大量的摩擦热.因此,在对关节轴承进行热分析时有必要考虑微凸体的影响.
在法向载荷作用下,两个粗糙表面相接触时,首先是微凸体开始互相接触.微凸体开始接触时为弹性变形,而后当载荷加载到某个临界数值后变成塑性变形, 此时微凸体是塑性变形而基体材料仍是弹性变形[1].
针对微凸体接触问题的建模及摩擦热的分析,国内外学者进行了一系列研究.对单个微凸体在圆形静止热源作用下的热问题,Gecim等[2]建立了二维瞬态热方程,分析了微凸体在几种不同边界条件下的温度分布. Ting等[3]分析了单个微凸体由于滑动摩擦热而导致的表面温升以及热应力问题.李隆球等[4]提出了一种在全滑移接触条件下,球形粗糙表面与刚性平面的弹塑性接触模型. Smith等[5]用有限元方法,研究了微凸体滑动接触过程中的闪点温度,并提出影响闪点温度的主要因素包括热导率、硬度、速度、摩擦因数、微凸体半径和微凸体磨损深度. Lee等[6]用数值方法分析了单对微凸体滑动接触过程中的瞬态导热问题,发现无量纲闪点温度仅仅是Peclet数的函数. Mate等[7]研究了磁记录头与磁记录盘上的微凸体在高速碰撞下的闪点温度.
在滑动摩擦过程中,滑动接触点成为热源,计算由摩擦热源引起的表面温升是研究热胶合的基础. Jaeger[8]计算了移动均匀热源作用下的半无限体的表面温升问题. Ashby等[9]给出了销盘模型干摩擦过程的闪温及体积温度的计算公式. Tian和Kennedy[10]基于Carslaw等[11]的热源法对不同形状热源下的半无限固体的最大闪温和平均温度进行了计算,并给出了微凸体接触过程中的最大闪温的近似表达式. Gao等[12]运用FFT方法求解了粗糙表面滑动摩擦的瞬态温度场. Bansal等[13]通过假设接触面对应各点温度相等,计算了一个球体相对平面滑动时的热流分配系数,并由此计算出接触面稳态温度分布.上述研究为进一步分析微凸体的滑动摩擦热问题提供了基础.
本文建立了关节轴承中的微凸体相对光滑平面滑动的模型,利用对点热源进行积分的方法分别计算了微凸体在弹性和塑性接触下的滑动接触面的稳态温度分布.并绘制了两种型号轴承在不同速度与载荷下接触面最高闪温图.
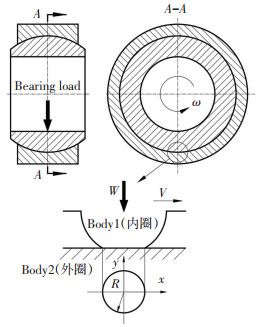
1 微凸体理论建模与求解如图 1所示,当内圈承受径向轴承力且绕轴线旋转时,接触面中心点处的线速度最大,接触压力较大,pv值较高,易出现热失稳.对该处的微凸体进行理论建模, 为了方便计算,对模型进行了如下简化:
|
图 1 微凸体-平面接触模型 Fig. 1 Contact model of asperity with plane |
1) 忽略润滑剂的影响,研究单个微凸体与平面接触的情况,微凸体出现在内圈上,形状为半球状,承受法向载荷W, 平面假设为光滑, 接触区的半径为R;
2) 由于微凸体尺度远小于轴承实体的尺度,故认为与微凸体相接触的外圈表面为平面,并且两个物体可以视为半无限体间接触;
3) 假设内外圈初始温度相等.
该圆形接触区为热源区,热源相对平面运动,相对微凸体静止.从相对运动的角度看,可认为该问题等价于微凸体静止而平面以速度V运动:
| $ V = \omega \cdot {R_0}. $ | (1) |
式中ω为轴承角速度,R0为内圈球半径.
当材料的热物性参数为常数时,直角坐标下的导热微分方程[14]为
| $ \frac{{{\partial ^2}\theta }}{{\partial {x^2}}} + \frac{{{\partial ^2}\theta }}{{\partial {y^2}}} + \frac{{{\partial ^2}\theta }}{{\partial {z^2}}} = \frac{1}{a}\frac{{\partial \theta }}{{\partial t}}. $ |
式中:θ为温升(℃);(x, y, z)为所计算点的坐标;t为时间(s);a为材料的热扩散系数(m2·s-1),a=λ·ρ-1cp-1;λ为材料导热系数(W·m-1·℃-1);ρ为密度(kg·m-3);cp为比定压热容(J·kg-1·℃-1).
两表面相对滑动时,假设摩擦力所做的功都转化为摩擦热,则接触面上单位面积产生的热流量为
| $ q = \mu pV. $ |
式中:q为热流密度(W·m-2), μ为摩擦因数, p为接触压力(Pa), V为两表面相对滑动速度(m·s-1).
接触面的热量将以一定比例分给上下两个物体:
| $ {q_1} = {K_1}\mu pV,\;\;\;\;{q_2} = \left( {1 - {K_1}} \right)\mu pV. $ | (2) |
式中,q1、q2分别为分配给物体1、2的热流密度,K1为物体1的热量分配系数.本文约定变量中下标为1表示微凸体,下标为2表示平面.
根据Carslaw和Jaeger[11]的研究:一个固定的点热源持续在一个移动半无限体表面上发热,将点热源坐标设定为笛卡尔坐标系的原点,则移动表面任意一点P(x, y, z)的稳态温升可以表示为
| $ \Delta \theta = Q/\left( {2{\rm{ \mathsf{ π} }}\lambda r} \right){{\rm{e}}^{\frac{{ - U}}{{2a}}\left( {r - x} \right)}}. $ |
式中:Q为该点热源产生的热流量(W);r=(x2+y2+z2)1/2,即为P点到该点热源的距离, 本文研究移动物体表面的温升,可令z=0;U为相对于热源的移动速度(m·s-1).
针对圆形热源作用的情况,可将热源区看成由无数个点热源组成,对每个点热源导致的温升进行积分,即可得到接触区各点的稳态温升.如图 2所示,利用极坐标对圆形热源区进行几何关系分析[10].

|
图 2 热源区极坐标示意图 Fig. 2 Polar coordinate system of heat source |
B点处的点热源产生的热流量为
| $ {\rm{d}}Q = q{\rm{d}}S = q{\rm{d}}s \cdot s{\rm{d}}\varphi . $ |
式中:dS为B点处热源微元的面积,q为该点的热流密度.将P(x, y)转化为极坐标P(r, α),B点的热源对P点造成的稳态温升可表示为
| $ \begin{array}{l} {\rm{d}}\theta = \frac{{{\rm{d}}Q}}{{2{\rm{ \mathsf{ π} }}\lambda s}}{{\rm{e}}^{\frac{{ - U}}{{2a}}\left[ {s - \left( {x - x'} \right)} \right]}} = \frac{{q{\rm{d}}s \cdot s{\rm{d}}\varphi }}{{2{\rm{ \mathsf{ π} }}\lambda s}}{{\rm{e}}^{\frac{{ - U}}{{2a}}\left[ {s - \left( {x - x'} \right)} \right]}} = \\ \;\;\;\;\;\;\;\;\frac{q}{{2{\rm{ \mathsf{ π} }}\lambda }}{{\rm{e}}^{\frac{{ - Us}}{{2a}}\left[ {1 - \cos \left( {\varphi - \alpha } \right)} \right]}}{\rm{d}}s{\rm{d}}\varphi . \end{array} $ |
P点在整个圆形热源作用下的温升可表示为
| $ \Delta \theta \left( {r,\alpha } \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}\lambda }}\int\limits_0^{2{\rm{ \mathsf{ π} }}} {\left( {\int\limits_0^{{s_1}} {q\left( {r,\alpha ,s,\varphi } \right){{\rm{e}}^{\frac{{ - Us}}{{2a}}\left[ {1 - \cos \left( {\varphi - \alpha } \right)} \right]}}{\rm{d}}s} } \right){\rm{d}}\varphi } . $ | (3) |
式中:s1为热源点与P点距离的积分上限,数值上等于直线BP与圆周交点到P点的距离:
| $ {s_1} = \sqrt {{r^2}{{\cos }^2}\varphi + \left( {{R^2} - {r^2}} \right)} - r\cos \varphi . $ | (4) |
q(r, α, s, φ)为热源点的热流密度,大小和微凸体的变形状态有关.
弹性变形状态下,接触压力为赫兹分布,因此热流密度可以写为
| $ \begin{array}{l} q\left( {r,\alpha ,s,\varphi } \right) = 3\mu {p_{\rm{m}}}V\sqrt {1 - {w^2}/{R^2}} /2 = \\ \;\;\;\;\;\;\;3\mu {p_{\rm{m}}}V/\left( {2R} \right)\sqrt {{R^2} - {r^2} - {s^2} - 2rs\cos \varphi } . \end{array} $ | (5) |
式中pm为接触面平均接触压力.
塑性变形状态下,接触面的压力可以看作恒定,平均接触压力等于两物体中较软材料的显微硬度H[1].因此热流密度可以写为
| $ q\left( {r,\alpha ,s,\varphi } \right) = \mu {p_{\rm{m}}}V = \mu HV. $ | (6) |
可以看出,弹性接触和塑性接触下的热源分别为抛物线分布和均匀分布.二者的最大表面温升经验公式如下[10]:
弹性接触,
| $ \Delta {\theta _{\max }} = 2.32Rq/\left( {\lambda \sqrt {{\rm{ \mathsf{ π} }}\left( {1.2344 + Pe} \right)} } \right); $ | (7) |
塑性接触,
| $ \Delta {\theta _{\max }} = 2Rq/\left( {\lambda \sqrt {{\rm{ \mathsf{ π} }}\left( {1.273 + Pe} \right)} } \right); $ | (8) |
式中,q为表面平均热流密度(W·m-2),Pe=UR·(2a)-1,是热力学中常用的无量纲数.
两个滑动体之间的热流分配采用的原则是:两表面最大温度相等[15].联立式(2)、(7)、(8)可以得到热流分配系数:
弹性接触,
| $ {K_1} = {\lambda _1}/\left( {{\lambda _1} + \sqrt {\frac{{1.2344 + P{e_2}}}{{1.2344 + P{e_1}}}} \cdot {\lambda _2}} \right); $ | (9) |
塑性接触,
| $ {K_1} = {\lambda _1}/\left( {{\lambda _1} + \sqrt {\frac{{1.273 + P{e_2}}}{{1.273 + P{e_1}}}} \cdot {\lambda _2}} \right). $ | (10) |
关于式(3),令U=0,可以算出微凸体在接触区域的表面温升.令U=V,可以算出平面在接触区域的表面温升.
联立式(1)~(5)、(9)可算出弹性接触状态下微凸体与平面的稳态温升,联立式(1)~(4)、(6)、(10)可算出塑性接触状态下微凸体与平面的稳态温升.
2 计算结果分析P26090B-G型航空用关节轴承材料参数如表 1所示,该轴承摩擦副为铜对钢,脂润滑状态下取摩擦因数μ=0.06,内圈球半径R0=1.98×10-2m.对关节轴承内圈进行高速精车,粗糙度达到Ra1.6,精度等级达到IT7~IT8左右,可以查阅得对应的微凸体折合曲率半径在20~55 μm[1],这里取40 μm.
| 表 1 P26090B-G型关节轴承材料参数 Tab. 1 Material parameters of spherical plain bearing(P26090B-G) |
弹性接触状态下,利用球体与平面接触的赫兹公式, 可得到接触半径和平均接触压力分别为
| $ R = {\left[ {\frac{{3W{r_0}}}{4}\left( {\frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}}} \right)} \right]^{1/3}}, $ | (11) |
| $ {p_{\rm{m}}} = W/\left( {{\rm{ \mathsf{ π} }}{R^2}} \right). $ | (12) |
式中,r0为微凸体球半径,E1、E2为微凸体和平面的弹性模量,υ1、υ2为两者的泊松比.
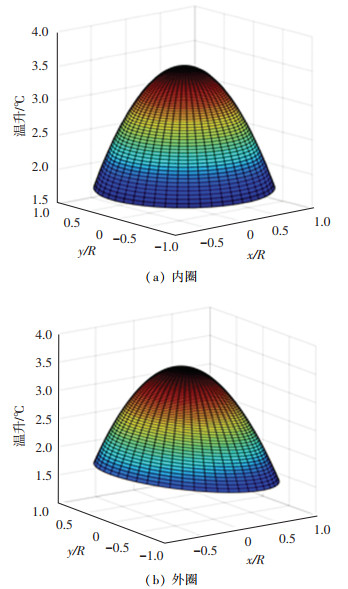
下面的算例中,取ω=20 rad·s-1,微凸体承载W=0.20 N,由式(11)、(12)可算出接触半径R=4.13 μm,平均接触压力pm=3.72 GPa.利用matlab编程并绘制出微凸体和平面在接触区的表面稳态温升,如图 3所示.
|
图 3 弹性接触区温升分布 Fig. 3 Temperature rise distribution in elastic contact zone |
由图 3可知,内圈微凸体在接触区的温升云图在x和y方向上都是对称的,最大温升Δθ=3.54 ℃,位于中心点.这是因为微凸体相对于接触区的热源是静止的,热量的传递不会受到相对滑动速度的影响.外圈接触区的温升云图在移动方向上(x轴方向)是非对称的,最大温升Δθ=3.53 ℃,位于中心点偏后沿的位置.并且,接触区后沿的温升明显大于前沿的温升.这是因为在运动过程中,前沿总是最后才与热源接触,热源作用时间短,温升小于已经率先与热源作用的接触区后沿.
由式(2)可知,摩擦热的产生与接触压力和相对速度有关,下面研究不同的载荷与速度下,外圈接触区沿x轴的的温升情况.
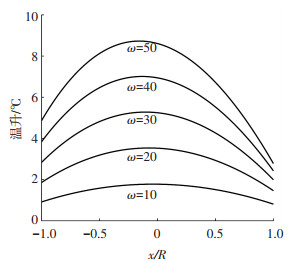
图 4为载荷0.20 N时,不同角速度ω(rad·s-1)下外圈接触区沿x轴处的温升情况.可以看出,随着速度的增加,温升增加,且后沿温升大于前沿温升的趋势越来越明显.这是因为滑动速度越大,所产生的摩擦热越多.且前沿与热流作用时间越短,导致前后沿温差越大.
|
图 4 弹性接触时不同角速度下的温升分布 Fig. 4 Temperature rise distribution under different angular velocity during elastic contact |
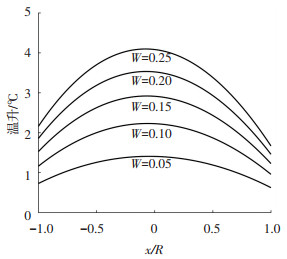
图 5为ω=20 rad·s-1时,不同载荷下的温升情况.可以看出,随着载荷的增加,温升增加.这是因为载荷越大,接触压力越大,摩擦热越多.
|
图 5 弹性接触时不同载荷下的温升分布 Fig. 5 Temperature rise distribution under different load during elastic contact |
塑性接触时pm恒为4.018 GPa,接触区半径
| $ R = {\left( {W/{p_{\rm{m}}} \cdot {\rm{ \mathsf{ π} }}} \right)^{1/2}}. $ | (13) |
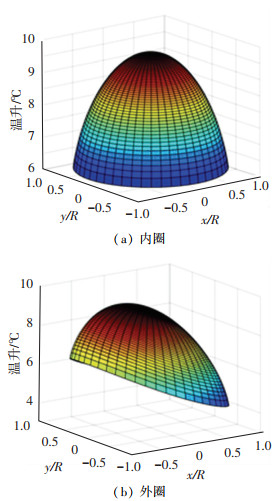
取ω=20 rad·s-1,W=2 N.由式(13)求得R=12.59 μm.计算出温升图如图 6所示.
|
图 6 塑性接触区温升分布 Fig. 6 Temperature rise distribution in plastic contact zone |
由图 6可知,内圈微凸体的最大温升Δθ=9.72 ℃,位于中心点.外圈的最大温升Δθ=9.50 ℃,位于中心点偏后沿的位置.接触区后沿的温升明显大于前沿的温升.
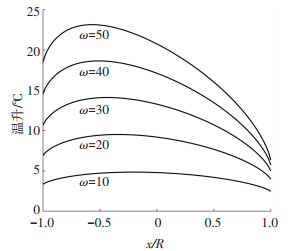
图 7为载荷2 N时,不同角速度下外圈接触区沿x轴的温升情况. 图 8为ω=20 rad·s-1时,不同载荷下的温升情况.二者的变化趋势与弹性状态下的类似.
|
图 7 塑性接触时不同角速度下的温升分布 Fig. 7 Temperature rise distribution under different angular velocity during plastic contact |

|
图 8 塑性接触时不同载荷下的温升分布 Fig. 8 Temperature rise distribution under different load during plastic contact |
由计算结果得知,塑性变形状态下最大闪温出现在x轴上.现给定线速度在0~5 m·s-1范围内变化,微凸体承载在0~30 N内变化,计算并绘制出最大闪温图见图 9.

|
图 9 最大闪温map图(P26090B-G型) Fig. 9 Map of maximum flash temperature for P26090B-G |
由图 9可知,当载荷与速度较高时,最大闪温值较大.而关节轴承往往在低速重载下工作,线速度通常不会超过1 m/s,因此微凸体的最大闪温值通常不会很大.但是有些偶发的工况值得考虑.以起落架用关节轴承为例,当飞机刚好落地时,轴承会承受较大冲击载荷,瞬时线速度也会很大.而根据Hou[16]的研究,移动热源作用的表面达到准稳态温度的时间为:
| $ t = 20a/{V^2}. $ | (14) |
式中:a为材料的热扩散系数,V为速度.由式(14)可求出,当速度为1 m·s-1时,t=0.098 ms.
在速度较大时,微凸体接触面会在极短的时间内达到最大温度.因此,在这些特殊工况下,微凸体接触面的最大闪温值较大.在实际的内外圈接触面上会有很多微凸体接触斑点,当它们达到最大闪温后,会加快表面损伤的劣化,影响润滑剂性能,严重时甚至会造成轴承胶合.而降低闪温值的方法主要有:改善润滑结构,提高关节轴承摩擦副的加工精度等.
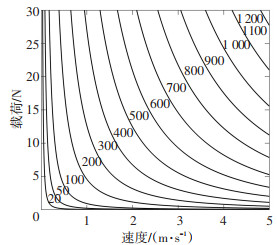
同理,可绘制出型号为WMLS17R型关节轴承的微凸体最大闪温图(图 10).
|
图 10 最大闪温map图(WMLS17R型) Fig. 10 Map of maximum flash temperature for WMLS17R |
关节轴承的材料参数如表 2所示.摩擦因数μ=0.12,内圈球半径R0=1.35×10-2m.
| 表 2 WMLS17R型关节轴承材料参数 Tab. 2 Material parameters of spherical plain bearing(WMLS17R) |
由图 10可知,在相同的速度和载荷下,WMLS17R型关节轴承的最大闪温值要明显大于P26090B-G型轴承.原因主要有:WMLS17R型轴承的摩擦因数大于P26090B-G型轴承,相同条件下会产生更多的摩擦热;WMLS17R型轴承内外圈摩擦副为钢对钢,而P26090B-G型为铜对钢.铜的导热系数大于钢,更利于摩擦热的传播.因此,WMLS17R型轴承更易发生热问题,不宜长期在高载荷和高转速的工况下工作.
4 结论1) 在弹性和塑性接触状态下,内圈微凸体在接触区的稳态温升分布形状为旋转体,最大温升位于中心点.外圈接触区的温升分布在移动方向上是非对称的,接触区后沿的温升大于前沿的温升,最大温升出现在中心点偏后沿的位置.
2) 微凸体载荷一定时,角速度越大,外圈接触区的温升越大,且前后沿的温差越大.角速度一定时,载荷越大,温升越大.
3) 低速重载工况下,微凸体最大闪温值较低; 而在高速情况下,最大闪温较大,会影响轴承性能.应注意这些情况下闪温值的控制. WMLS17R型轴承应比P26090B-G型轴承更易发生热问题,不宜长期在高载荷和高转速的工况下工作.
| [1] |
克拉盖尔斯基И B. 摩擦、磨损与润滑手册:第一册[M]. 北京: 机械工业出版社, 1986: 23. КРАГЕЛВСКИЙ И B. Handbook on friction, wear and lubrication (volume 1)[M]. Beijing: Mechanical Industry Press, 1986: 23. |
| [2] |
GECIM B, WINER W O. Transient temperatures in the vicinity of an asperity contact[J]. Journal of Tribology, 1985, 107(3): 333. DOI:10.1115/1.3261068 |
| [3] |
TING B Y, WINER W O. Friction-induced thermal influences in elastic contact between spherical asperities[J]. Journal of Tribology, 1989, 111(2): 315. DOI:10.1115/1.3261916 |
| [4] |
李隆球, 王林, 张广玉, 等. 全滑移下球形粗糙表面的弹塑性接触模型[J]. 哈尔滨工业大学学报, 2012, 44(9): 62. LI Longqiu, WANG Lin, ZHANG Guangyu, et al. Elastic-plastic model for rough spherical contact in slip contact condition[J]. Journal of Harbin Institute of Technology, 2012, 44(9): 62. DOI:10.11918/j.issn.0367-6234.2012.09.011 |
| [5] |
SMITH E H, ARNELL R D. A new approach to the calculation of flash temperatures in dry, sliding contacts[J]. Tribology Letters, 2013, 52(3): 407. DOI:10.1007/s11249-013-0224-9 |
| [6] |
LEE Y, LIU Y, BARBER J R, et al. Thermal considerations during transient asperity contact[J]. Tribology International, 2016, 94: 87. DOI:10.1016/j.triboint.2015.08.008 |
| [7] |
MATE C M, DENG H, LO G J, et al. Measuring and modeling flash temperatures at magnetic recording head-disk interfaces for well-defined asperity contacts[J]. Tribology Letters, 2015, 58(2): 1. DOI:10.1007/s11249-015-0505-6 |
| [8] |
JAEGER J C. Moving sources of heat and the temperature of sliding contacts[J]. J and Proc Roy Soc New South Wales, 1942, 76: 203. |
| [9] |
ASHBY M F, ABULAWI J, KONG H S. Temperature maps for frictional heating in dry sliding[J]. Tribology Transactions, 1991, 34(4): 577. DOI:10.1080/10402009108982074 |
| [10] |
TIAN X, KENNEDY F E. Maximum and average flash temperatures in sliding contacts[J]. Journal of Tribology, 1994, 116(1): 167. DOI:10.1115/1.2927035 |
| [11] |
CARSLAW H S, JAEGER J C. Conduction of heat in solids[M]. New York: Oxford University Press, 1959: 1.
|
| [12] |
GAO J, LEE S C, AI X, et al. An FFT-based transient flash temperature model for general three-dimensional rough surface contacts[J]. Journal of Tribology, 2000, 122(3): 519. DOI:10.1115/1.555395 |
| [13] |
BANSAL D G, STREATOR J L. A method for obtaining the temperature distribution at the interface of sliding bodies[J]. Wear, 2009, 266(7): 721. DOI:10.1016/j.wear.2008.08.019 |
| [14] |
杨世铭, 陶文铨. 传热学[M]. 第4版. 北京: 高等教育出版社, 2006: 43. YANG Shiming, TAO Wenquan. Heat transfer[M]. 4th edition. Beijing: Higher Education Press, 2006: 43. |
| [15] |
KENNEDY F E. Thermal and thermomechanical effects in dry sliding[J]. Wear, 1984, 100(1/2/3): 453. DOI:10.1016/0043-1648(84)90026-7 |
| [16] |
HOU Z B, KOMANDURI R. General solutions for stationary/moving plane heat source problems in manufacturing and tribology[J]. International Journal of Heat and Mass Transfer, 2000, 43(10): 1684. DOI:10.1016/s0017-9310(99)00271-9 |
 2020, Vol. 52
2020, Vol. 52


