2. 广东省智能制造研究所 广东省现代控制技术重点实验室,广州 510070
2. Guangdong Key Laboratory of Modern Control Technology, Guangdong Institute of Intelligent Manufacturing, Guangzhou 510070, China
随着协作型机器人的广泛应用与发展,未来机器人必将逐渐地由传统封闭的制造业环境向与人交互、共融的共享空间迈进,由半自动的操作任务到更加自主完成的执行任务[1].从而,不可避免地存在各类异常发生的情况,例如:出现了人类无意识地与机器人手臂碰撞、视觉传感信息存在偏差造成夹子与物体发生碰撞、夹取的物体在运动过程中滑落及机器人内部传感器的异常发生等等.另外,伴随着机器人对环境感知能力的改善,机器人在执行过程中更加依赖于多模态的传感信息[2],比如通过力/力矩传感器能有效地感知所抓取物体的重量及是否与外界发生碰撞、机器人关节编码器能实现对机器人构型的运动控制以及通过触觉传感器判断是否抓取到物体.近年来,研究表明实现基于多模态时间序列建模的机器人安全监控将有助于人-机安全共融操作及更长期可靠的机器人自主执行[3-5].如何有效地解决此问题是目前机器人操作领域的研究重点及难点.
文献[3]基于隐马尔可夫模型(HMM)提出了一种用于机器人装配任务的过程监测器.该监测器首先对机器人的装配任务通过离散的事件进行描述,然后对装配过程中所产生力/力矩的传感信号进行建模.最后在给定隐性状态数量的前提下,每个事件的HMM参数采用Baum-Welch离线学习方法获得.文献[4-6]提出了一种基于从左向右的HMM模型(Left-to-right HMM)应用于多模态的机器人异常检测系统.该系统考虑机器人在执行过程的多模态传感信息(力/力矩、声音和视觉)对机器人异常检测的影响.通过建立机器人的执行过程与观察数值的对数似然函数值的映射关系实现了异常检测,并提出了动态阈值的计算方法.但是,传统的HMM模型在应用于多模态时间序列的情况下,具有两个关键的问题:1)在模型学习之前需要给定隐性状态的数量,限制了对传感数据的建模能力;2)没有考虑时间序列的一致性,也就是说,隐性状态不合理地快速转换,而机器人实际的执行过程应该保持一定的时间依赖性.比如,当规划机器人去抓取桌上的一个杯子时,希望机器人在靠近杯子过程中的观察值始终归类到相同的隐性状态下.
针对参数化HMM中存在的两个问题,文献[7]提出了一个贝叶斯非参数模型,即多模态粘性层级狄利克雷过程隐马尔可夫模型(MD-sHDP-HMM).该模型是在HDP-HMM[8]的基础上引入粘性先验和多模态观测分布而形成的,保持了HDP-HMM的所有优点,但比HDP-HMM具有更宽的适用范围和更强的鲁棒性,可以对类内差异大、单时刻有多个观测的复杂时间序列建模. MD-sHDP-HMM模型能有效地从训练数据集中推断出最优的隐性状态数量,并且借助了“粘性”(sticky)的性质增加了隐性状态自转换的期望概率,提高了时间序列相邻数据间的依赖性,已广泛应用于复杂时间序列中的运动模式学习,如语音分类[9]和人类动作的识别[10].基于贝叶斯非参数模型在多模态时间序列应用中的性质,文献[11]利用HDP-HMM实现了机器人装配任务过程中的异常检测.首先把机器人执行的电子元件装配任务分割成有限个子任务,并利用有限状态机对任务进行描述,然后在机器人重复执行正常任务的过程中采集力/力矩数据,最后采用HDP-HMM对各个子任务的数据进行建模,实现了机器人异常的监测.但是,没有对机器人的执行过程进行识别、仅考虑了力/力矩信号的作用,降低了机器人对环境的感知能力以及在模型未知参数推断方面采用传统的Gibbs采样方法,造成严重低下的计算效率.
本文采用了MD-sHDP-HMM对多模态传感数据进行建模,通过贝叶斯变分推断的方法(Bayesian Variational Inference)进行参数的学习,大幅度提高了训练模型的准确性和减少了计算的复杂度.所提出的方法首先对机器人的执行任务分割成序列化的执行过程,然后通过对比执行过程中累积观察数据的对数似然函数值的大小实现执行过程的识别.在此基础上,根据正常执行过程训练得到的对数似然函数值的梯度阈值,实现了机器人执行过程中的实时异常监测.最终有效地实现了多模态时间序列建模的机器人安全监控.
1 机器人精准感知系统框架我们在前期的工作[12]中已提出了使用MD-sHDP-HMM实现机器人在电子元件装配和拾放任务过程中的精准感知.所谓的感知即是让机器人解析自己目前正在执行的过程,有助于解决机器人执行过程的识别问题.针对机器人安全监控的问题展开研究,在传统机器人控制框架Sense-Plan-Act的基础上增加了用于机器人执行过程识别及异常监控的感知(Introspection)阶段,提出了一个名为SPAI(Sense-Plan-Act-Introspection)系统框架,如图 1所示.机器人的复杂任务通过有向图的形式描述,每个节点具有两项功能:一方面用于表示机器人各运动基元的始点或终点,生成机器人的运动,即图 1中的M所示;另一方面是感知功能,用于执行过程识别与异常监测,即图 1的I所示.该系统框架主要包括了4个功能模块:任务描述、运动生成、精准感知以及异常修复.任务描述模块主要是对机器人实际操作的复杂任务分割成序列化的运动基元,然后利用有限状态机(Finite State Machine)人为地根据任务的执行次序构建机器人自主操作图,如图 1中从开始节点到完成节点的有向图表示;运动生成模块将借助于示范学习(Learning from demonstration)的框架对人类示教的过程进行学习与泛化,有利于提高机器人任务的多样化和执行过程的不确定性;精准感知模块主要包括对机器人当前执行过程的识别以及外部异常的监测;异常修复模块用于对监测到的异常进行分类并执行相应的修复策略.
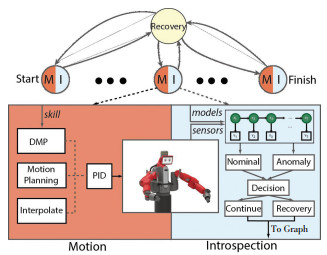
|
图 1 机器人安全监控系统框架 Fig. 1 Framework of robot surveillance system |
近年来,HMM已广泛应用于语音识别、视觉行为分析和异常检测等领域.在使用连续HMM对多模态时间序列建模的基础上进行机器人或人类的异常行为进行识别,有助于实现人-机交互过程中的安全共融和更长期的机器人自主操作[13-14]. 图 2显示了层级HMM的概率图模型. HMM通过隐马尔科夫链假设实现在任意时刻t的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻t无关.另外,HMM假设在任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测状态无关.因此,HMM模型的观察数据与隐性状态的联合分布表示为
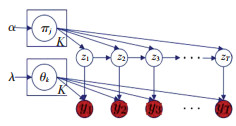
|
图 2 HMM的概率图描述 Fig. 2 Graphical representation of HMM |
| $ \begin{array}{l} p\left( {{y_1}, \ldots ,{y_T},{z_1}, \ldots ,{z_T}} \right) = \\ \;\;\;\;\;\;\;p\left( {{z_1}} \right)\prod\limits_{t = 2}^T p \left( {{z_t}|{z_{n - 1}}} \right)\prod\limits_{t = 1}^T p \left( {{y_t}|{z_t}} \right). \end{array} $ | (1) |
由式(1)可知,HMM模型由三项概率分布组成.p(z1)表示初始隐性状态的概率分布,由超参数α决定;p(zt|zn-1)表示隐性状态间的转移概率;p(yt|zt)表示给定隐性状态下观察数据的概率分布,不同的观察值分布由超参数λ决定.特别地,本文采用多变量高斯分布(Multivariate Gaussian Distribution)作为观察模型.
从而,当多模态的时间序列由HMM建模后,即可以用来解决3个问题,首先是参数学习的问题,即给定观察序列学习HMM的所有参数θ.其余2个同属于模式识别的问题,分别是评估问题和解码问题:给定θ计算求解一段观察序列的概率值;给定观察序列求解最优的隐性状态序列.本文对于机器人的安全监控主要利用了对评估问题和解码问题的求解.
2.2 粘性层级狄利克雷过程隐马尔可夫模型机器人安全监控实现流程如图 3所示.本文在考虑参数化HMM的局限性下,采用贝叶斯非参数模型构建粘性层级狄利克雷过程隐马尔可夫模型.首先,假设离散的分布G是一个对数据聚类的过程,它来自于DP (Dirichlet Process),那么

|
图 3 机器人安全监控实现流程图 Fig. 3 Implementation flowchart of robot safety surveillance |
| $ G \sim {\rm{DP}}\left( {\gamma ,H} \right), $ | (2) |
其中,H可以是任意的基分布,γ为集中系数.层级狄利克雷过程HDP(Hierarchical Dirichlet Process)是狄利克雷过程DP的一种扩展形式,它主要用于解决在DP中,当基分布是连续时所得到的采样参数与概率1不等的情况[15]. HDP通过在基分布上又定义了一个先验分布,由每个DP获得基分布的采样,这样就保证了基分布的离散性.由式(2)可知HDP的定义如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{G_0}|H,\gamma \sim {\rm DP}\left( {\gamma ,H} \right),}\\ {{G_j}|{G_0},\alpha \sim {\rm DP}\left( {\alpha ,{G_0}} \right).} \end{array}} \right. $ | (3) |
同理,可以利用HDP对HMM模型的隐性状态转换概率πj的进行一般性的描述如下:
| $ \left\{ \begin{array}{l} \beta \left| {\gamma \sim {\rm{GEM}}\left( \gamma \right)} \right.,\\ {G_0} = \sum\limits_{k = 1}^\infty {{\beta _k}{\delta _{{\theta _k}}}} \sim {\rm DP}\left( {\gamma ,H} \right);{\theta _k}\left| {H \sim H} \right.;\\ {\pi _j}|\beta ,\alpha \sim {\rm DP}\left( {\alpha ,\beta } \right),j = 1,2, \ldots . \end{array} \right. $ | (4) |
其中,GEM表示折棍子的生成过程[16],由此可见集中系数γ决定了β的相对离散比例,当γ越大表示数据越离散,反之,越集中.通过对HMM的状态转换概率增加HDP先验,即可获得HDPHMM模型,如图 4左图所示.注意到HDP先验使得对数据的聚类数量是不确定的,从而能有效地解决了传统HMM中给定隐性状态的局限性.另外,在DP过程中增加“粘性”参数κ,提高隐性状态的自我转换概率,即
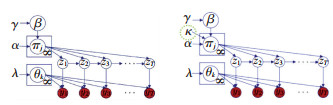
|
图 4 HDPHMM(左)和sHDPHMM(右)的概率图模型 Fig. 4 Graphical representation ofHDPHMM and sHDPHMM |
| $ {\pi _j}\left| {\alpha ,\kappa ,\beta } \right. \sim {\rm DP}\left( {\alpha + \kappa \frac{{\alpha \beta + \kappa {\beta _j}}}{{\alpha + \kappa }}} \right). $ | (5) |
使得HDPHMM对序列数据建模时有更好的时间依赖性,这样将加强模型的实际应用性,如图 4右图所示.所构建好sHDPHMM模型的所有未知参数Θ可以通过贝叶斯变分推断的方法[17]实现.由建立好的统计学模型可以用于对机器人执行任务进行安全监控,总体的实现流程如图 3所示.
3 机器人执行过程的识别由图 3中A所示,机器人的操作任务被分解成多个执行过程S的形式,对于某一个执行过程s∈S的识别主要是使得机器人在执行任务过程中感知到自己目前所在那段执行过程.同时,也能有效地验证所建立模型对该过程产生传感数据的建模能力.假设执行过程s的模型参数为Θs,由HMM的性质可知,给定观察序列y1:t=[y1, y2, ..., yt],利用前向-反向算法[18]求得模型s在时刻t的对数似然函数值Lt, s,即
| $ {L_{t,s}} = \log p\left( {{y_{1:t}}\left| {{\mathit{\Theta }_s}} \right.} \right) = \sum\limits_{i = 1}^t {\log p\left( {{y_t}\left| {{y_{t - 1}}} \right.;{\mathit{\Theta }_s}} \right)} . $ | (6) |
注意这里的yt表示机器人执行过程中的观察值.本文中的观察值是一个18位的向量,详见5.2节. Lt, s表示了观察数据在给定模型下的分值,分值越高表明该数据越贴近该模型的分布.基于这样的设想,机器人执行过程的识别可以通过找出最大化当前所观察序列数据的分值.也就是说,给定测试任务样本r,首先,将r分解成S个执行过程,然后分别求解各个执行过程模型下的分值log p (y1:t|Θs)sS,那么执行过程的识别可以由下式得到:
| $ {s^ * } = \mathop {\arg \max }\limits_{s \in S} \left( {{L_{t,s}}} \right). $ | (7) |
然而,在实际应用中发现,对于直接利用Lt, s的数值大小进行执行过程识别会造成较大的误差,甚至错误,详细的结果见5.3节.针对此问题,本文分析了HMM模型的前向算法发现,可以通过计算时刻t的可信状态(belief state)的方式来预测t+1时刻数据的概率值.由此,通过计算似然函数的梯度值的方式来实现执行过程的识别,即
| $ {G_{t,s}} = {L_{t,s}} - {L_{t - 1,s}}. $ | (8) |
同理地得到
| $ {s^ * } = \mathop {\arg \max }\limits_{s \in S} \left( {{G_{t,s}}} \right). $ | (9) |
在实际应用中,通过对比各个时刻t对应所有执行过程模型的似然函数的梯度值便可.
4 机器人异常事件的监测基于上章节机器人执行过程的识别后,本节详细介绍机器人的异常事件监测的实现,如图 3中的F阶段.本文实现异常检测的主要思路是:首先,学习正常执行的数据模型;然后,基于此模型测试正常执行过程的数据,以求得正常与异常的边界定义,也就是异常阈值的计算;最后,基于该模型和对应的阈值实现对测试样本的预测.
4.1 异常检测的实现在执行过程识别之后,假设已知特定的执行过程s及其所建立模型的参数为Θs.众所周知,机器人正常地重复执行过程s将产生相似的传感数据,也就是说,对在任一时刻其所求解得到对数似然函数值在一定的倍数的方差值内.本文设定机器人正常地重复执行过程s的次数为N(一般地,N>20),其中用于测试的数量是Ne=0.4N.那么,基于Ne个测试样本所得到Ne个对数似然函数值的向量为
| $ \left\{ {\begin{array}{*{20}{l}} {\mu \left( {{L_{t,s}}} \right) = \frac{1}{{{N_e}}}\sum\limits_{n = 1}^{{N_e}} {L_{t,s}^n} ,}\\ {\mu \left( {L_{t,s}^2} \right) = \frac{1}{{{N_e}}}\sum\limits_{n = 1}^{{N_e}} {{{\left( {L_{t,s}^n} \right)}^2}} ,}\\ {\sigma \left( {{L_{t,s}}} \right) = \sqrt {\mu \left( {L_{t,s}^2} \right) - {{\left( {\mu \left( {{L_{t,s}}} \right)} \right)}^2}} .} \end{array}} \right. $ | (10) |
由式(10),可知每个时刻t的异常监测阈值为
| $ {\rho _{t,s}} = \mu \left( {{L_{t,s}}} \right) - c \cdot \sigma \left( {{L_{t,s}}} \right). $ | (11) |
其中,c表示比例常数.因此,机器人在实际操作过程中,当Lt, s < ρt, s表示监测到异常的发生,反之,正常执行.
在实际应用中发现,通过式(11)得到的阈值使得异常监测器出现频繁的错误触发(False Positive),意味着把正常的执行情况监测成为了异常.另外,对于常数变量c的确定需要进行繁琐的交互验证.针对此问题,本文参照机器人执行过程识别的经验,通过求解每个对数似然函数值向量的梯度值信息来确定异常发生的阈值.
4.2 梯度阈值的定义本章节阐述梯度阈值的实现.假定执行过程s的Ne个正常测试样本的对数似然函数值的向量为
| $ \left\{ \begin{array}{l} {G_{\max ,s}} = \mathop {\max }\limits_{n \in \left\{ {1, \ldots ,{N_e}} \right\}} \left( {\mathop {\max }\limits_{t \in \left\{ {1, \ldots ,{T_s} - 1|} \right.} \left( {G_{t,s}^n} \right)} \right),\\ {G_{\min ,s}} = \mathop {\min }\limits_{n \in \left\{ {1, \ldots ,{N_e}} \right\}} \left( {\mathop {\min }\limits_{t \in \left\{ {1, \ldots ,{T_s} - 1|} \right.} \left( {G_{t,s}^n} \right)} \right). \end{array} \right. $ | (12) |
然后,由式(12)求解执行过程s所有正常测试样本的取值范围
| $ {G_{{\rm{range}},s}} = {G_{{\rm{max}},s}} - {G_{{\rm{min}},s}}. $ | (13) |
最后,用于异常监测的梯度阈值可以定义如下:
| $ {\rho _s} = {G_{\min ,s}} - 0.5{G_{{\rm{range}},s}}. $ | (14) |
由此,给定的机器人的执行过程,该阈值为一个常数,当任一时刻t求得似然函数的梯度值Gt, s < ρs时,监测到异常,否则表示正常执行.
5 实验结果与分析 5.1 实验方案与信号预处理本文所提出的方法将通过一个Baxter机器人与人类协作完成物品装箱的任务进行验证,图 5(a)显示了整个实验平台的设计环境.设定Baxter机器人的右手臂用于抓取和放置6种不同形状或重量的物品到固定的快递盒中(位于图像的最左侧). Baxter机器人由左手臂运动到一个固定的位姿,以便其末端的摄像头能准确地检测到物体表面的标记.其中,右手末端关节与夹子之间装有一个6维的力/力矩传感器,夹子的两手指分别装有一个7×4矩阵分布的触觉传感器;物体表面的标注用于对物体进行位姿估计.该任务的实现过程是人类逐一地把物品放在相机的视野区域内,通过左手相机的物体定位,然后机器人按照预先定义好的5个操作过程进行执行任务,分别是:起始点→预抓取点、预抓取点→抓取点、抓取点→预抓取点、预抓取点→预放置点和预放置点→放置点,各个过程分别对应于如图 5(b)~(f)所示.

|
图 5 实验测试平台:Baxter机器人执行物品装箱 Fig. 5 Testbed: Baxter robot performing kitting experiment |
本文将考虑3种模态的传感信息:机器人末端关节的速度信号、力/力矩传感信号及两个手指的触觉信号.特别地,原始的机器人末端关节的速度信号包括了三维线速度和三维角速度信号,力/力矩传感信号包括了三维力信号和三维力矩信号,每个触觉传感器将产生28维的信息.若直接对所有68维的传感信号进行建模将增加了大量冗余的信息,并且加剧了计算的效率.另外,为了考虑机器人执行任务的速度不同和操作物体的重量不同等因素.本文所考虑的传感信息包括原始的6维末端速度信号和其对应2维的模向量、原始的6维力/力矩信号和其对应2维的模向量及2维触觉传感器的标准差信号.综上所述,每时刻所考虑的传感信息是一个18维的向量.
5.2 模型的训练与测试如图 5所示,本文所考虑的机器人任务包含了5个执行过程.针对实验分析的过程分为两大类:正常任务的数据采集以及异常任务的测试.正常任务的数据采集是用于学习正常的统计学模型,主要是通过5个参与者分别独立完成一整组物品装箱的实验,由上述可知每组实验包含6个不同的物体,从而,总共采集了正常执行的任务数量是30次.其中,用于训练的任务的数量是18,用于测试的数量是12.另外,对于异常任务的执行,同样是5个参与者分别独立完成一整组物品装箱的实验,不同的是在任务执行过程中人为地或者机器人自身产生一次或多次异常的情况,以用于验证异常监测的有效性.
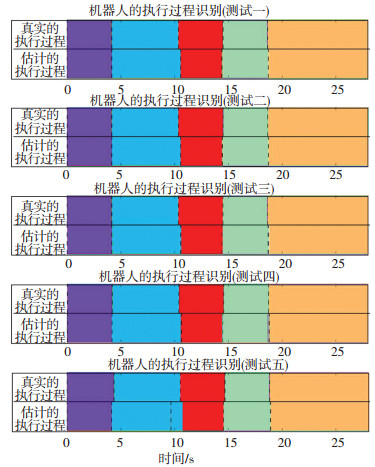
5.3 机器人执行过程识别由章节3可知,对于机器人执行过程的识别是通过计算任一时刻观察在所有学习好的模型下的对数似然函数值的梯度值实现的,参考式(9)可知.如图 6所示,显示了针对同一测试任务下,对数似然函数值曲线和梯度曲线的对比图.由图中可知,不同颜色的曲线代表不同执行过程模型下所计算得到的数值,考虑似然函数梯度值的情况下才能清楚地识别出不同执行过程的转换.如图 7所示,分别显示了机器人5次正常操作任务的执行过程识别结果,不同颜色的背景条框分别代表 5个不同的MD-sHDPHMM模型,各个子图中的上半部分表示了人为分解任务的真实值,下半部分是通过梯度值估计的执行过程分解结果.由此,可见本文所提出方法能有效地和准确地应用于机器人复杂任务下的执行过程识别.
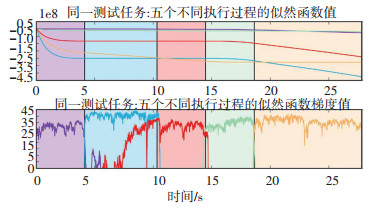
|
图 6 同一测试任务下,对数似然函数值和梯度曲线图.不同颜色的曲线代表不同执行过程模型下所计算得到的数值 Fig. 6 Log-likelihood and gradient-based log-likelihood of a testing task. The curves in different colors represent the values calculated under different execution process models |
|
图 7 机器人执行过程识别 Fig. 7 Identification of robot executing process |
由第4章节的定义可知,在给定识别的机器人执行过程之后,通过实时地计算当前时刻观察数据的对数似然函数梯度值实现异常事件的监测.本文对比了同一个异常或正常测试任务下,利用对数似然函数值或对数似然函数梯度值进行异常监测的情况,如图 8所示.图中各个子图中不同颜色的背景条框分别代表 5个不同的MD-sHDPHMM模型,由此可以得知:1)在异常任务测试中,竖向红色实线表示人为记录异常发生的时刻,总共有8次异常的发生.另外,横向红色虚直线表示了不同时刻的异常阈值;2)对异常任务的监测中,对数似然函数梯度值更能准确地触发异常,而对数似然函数值将会引起大量的误判(False Positive)及没有监测到的情况(False Negative);3)对正常任务的监测中,对数似然函数梯度值没有监测到任何的异常,但是对数似然函数值同样地出现了严重的误判.
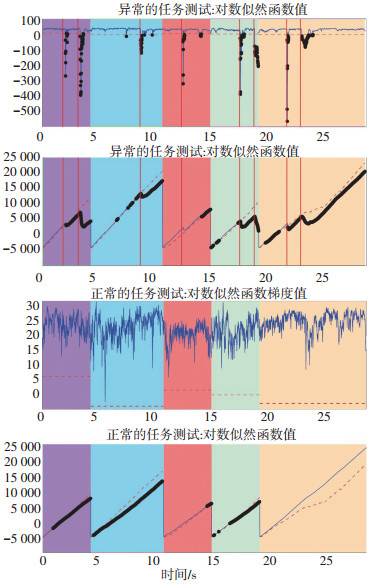
|
图 8 机器人异常事件监测的验证 Fig. 8 Evaluation of robot anomaly event detection |
参照章节5.2的说明,对总共30次可能发生异常的操作任务进行总体的异常监测性能分析.通过把异常事件的监测定义为一个二分类的问题,即是把测试事件归类为异常与正常的两类.再者,假设人为记录异常发生的时刻为真实值,即图 8中的竖向红色实线所示,若异常监测触发的时刻与该真实值的差距小于1s定义为正确检测(Ture Positive).最后,考虑了精确率(Precision)、召回率(Recall)和准确率(Accuracy)作为评价的指标对比文中提到的两种异常监测方法的性能,其中对数似数函数值作为阈值的方法(见式(11),常数c=3)简写为“似值”,梯度阈值的方法(见式(14))简写为“梯值”,具体的结果如表 1所示.
| 表 1 异常事件监测的性能对比 Tab. 1 Performance comparison of anomaly event detection |
从表 1中结果可知,似然函数的异常监测的平均精确率仅为85%,相比于梯度阈值的方法表示出现了更多的误判,如图 8中第四个子图所示;召回率较低的结果表明似然函数的异常监测方法对于异常的事件有严重遗漏检测的情况.综上所述,本文所提出基于对数似然函数梯度阈值的方法对于总共67次异常检测的平均监测准确率为93.8%.
6 结语本文针对多模态时间序列建模的机器人安全监控的问题,借助于前期提出的机器人感知系统框架, 采用了MD-sHDPHMM对多模态传感信息进行建模.得益于该模型的强大建模能力,深入分析模型的似然函数计算过程,首先提出了基于对数似然函数梯度值的机器人执行过程识别,随后借助优秀的执行过程识别的实现,提出了基于对数似然函数梯度阈值的机器人异常监测.实验结果表明,提出的机器人执行过程识别与机器人异常监测的方法对所设计实验的总体异常监测精确率为95.2%,召回率为94.2%及准确率为93.8%,有效地实现了机器人自主操作或与人类交互过程中的安全监控,并且集成于SPAI系统框架中,易于扩展到其他的机器人平台及不同的操作任务,对未来机器人的普及具有重要的研究与应用价值.
| [1] |
张含阳. 人机协作:下一代机器人的必然属性[J]. 机器人产业, 2016(3): 37. ZHANG Hanyang. Human-robot collaboration: an essential attribute of the next generation of robotics[J]. Robotics Industry, 2016(3): 37. |
| [2] |
孙晓莉. 多传感器信息融合在机器人技术中的应用[J]. 无线互联科技, 2018(2): 130. SUN Xiaoli. Application of multisensor information fusion in robotics[J]. Wireless Internet Technology, 2018(2): 130. DOI:10.3969/j.issn.1672-6944.2018.02.063 |
| [3] |
HOVLAND G, MCCARRAGHER B J. Hidden Markov models as a process monitor in robotic assembly[J]. The International Journal of Robotics Research, 1998, 17(2): 153. |
| [4] |
PARK D, ERICKSON Z, BHATTACHARJEE T, et al. Multimodal execution monitoring for anomaly detection during robot manipulation[C]//Robotics and Automation (ICRA), IEEE International Conference on. Stockholm: IEEE, 2016: 407
|
| [5] |
PARK D, KIM H, HOSHI Y, et al. A multimodal execution monitor with anomaly classification for robot-assisted feeding[C]//Intelligent Robots and Systems (IROS), IEEE/RSJ International Conference on. Vancouver: IEEE, 2017: 5406
|
| [6] |
PARK D, KIM H, KEMP C C. Multimodal anomaly detection for assistive robots[J]. Autonomous Robots, 2019, 43(3): 611. DOI:10.1007/s10514-018-9733-6 |
| [7] |
FOX E B, SUDDERTH EB, JORDAN M I, et al. The sticky HDP-HMM: Bayesian nonparametric hidden Markov models with persistent states[J]. Arxiv Preprint, 2007. |
| [8] |
THE Y W, JORDAN M I. Hierarchical Bayesian nonparametric models with applications[J]. Bayesian Nonparametrics, 2010, 1: 158. |
| [9] |
NEJAD TORBATI A H, PICONE J, SOBEL M. A left-to-right HDP-HMM with HDPM emissions[C]//Information Sciences and Systems (CISS), 48th Annual Conference on. Princeton, NJ: IEEE, 2014: 1
|
| [10] |
RAMAN N, MAYBANK S J. Action classification using a discriminative multilevel HDP-HMM[J]. Neurocomputing, 2015, 154: 149. DOI:10.1016/j.neucom.2014.12.009 |
| [11] |
LELLO E D, KLOTZBUCHER M, LAET T D, et al. Bayesian time-series models for continuous fault detection and recognition in industrial robotic tasks[C]//Intelligent Robots and Systems (IROS), IEEE/RSJ International Conference on. Tokyo: IEEE, 2013: 5827
|
| [12] |
WU Hongmin, LIN Hongbin, GUAN Yisheng, et al. Robot introspection with Bayesian nonparametric vector autoregressive hidden Markov models[C]//Humanoid Robotics (Humanoids), IEEE-RAS 17th International Conference on. Birmingham: IEEE, 2017: 882
|
| [13] |
LAU H Y K. A hidden Markov model-based assembly contact recognition system[J]. Mechatronics, 2003, 13(8-9): 1001. DOI:10.1016/S0957-4158(03)00012-6 |
| [14] |
FOX M, GHALLAB M, INFANTES G, et al. Robot introspection through learned hidden markov models[J]. Artificial Intelligence, 2006, 170(2): 59. DOI:10.1016/j.artint.2005.05.007 |
| [15] |
曹建凯, 张连海. 采用HDPHMM符号化器的语音查询样例检测方法[J]. 信号处理, 2017(5): 703. CAO Jiankai, ZHANG Lianhai. Query-by-example spoken term detection by applying the HDPHMM tokenizer[J]. Journal of Signal Processing, 2017(5): 703. |
| [16] |
SETHURAMAN J. A constructive definition of Dirichlet priors[J]. Statistica Sinica, 1994, 4(2): 639. |
| [17] |
HUGHES M C, SUDDERTH E B. Bnpy: reliable and scalable variational inference for Bayesian nonparametric models[C]//NIPS Probabilistic Programimming Workshop. 2014
|
| [18] |
FOX E B. Bayesian nonparametric learning of complex dynamical phenomena[D]. Boston: Massachusetts Institute of Technology, 2009
|
 2020, Vol. 52
2020, Vol. 52


