2. 中国科学院大学,北京 100049;
3. 中国科学院大学 微电子学院,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Microelectronics, University of Chinese Academy of Sciences, Beijing 100049, China
卫星钟差预报是导航定位中一项至关重要的工作之一[1-2].星载原子钟因其自身的性能以及所处空间复杂环境的影响, 钟源偏差需要与地面站的原子钟进行比对并校准以保持比较精确的时间信息, 但是出于某些原因星载原子钟无法与地面站保持比对的时候就需要采用已有的钟差信息进行预报.在这段时间内, 卫星以预报的星历信息进行自主完成轨道确定和广播星历的播发, 这对于卫星的自主生存能力具有重要影响[3-4], 所以如何提高卫星钟差预报的精度和稳定度一直以来都是国内外研究的热点问题之一.
长久以来, 在卫星钟差预报方面, 国内外许多学者进行了多角度、多方位和深层次的研究, 并取得了一系列重要研究成果[5-7].其中, 灰色系统预报模型只需要少量的钟差数据建模就可以预报, 并且需要数据平滑且呈类指数变化, 对于数据呈非指数变化的钟差预报效果较差等特点.文献[8]提出采用最小一乘法准则去估计灰色模型的参数, 以克服在钟差波动较大的情况下最小二乘法准则估计参数预报精度的不足, 并且通过预报试验证明了算法的有效性.文献[9]提出了一种先用对数平滑处理的方法对原始钟差数据序列进行平滑处理, 再使用自适应双子群改进粒子群算法来优化灰色模型的发展系数和灰作用量的预报策略, 从而增强了灰色模型的泛化能力.文献[10]提出先对卫星钟差第一天偶数整时的值采用灰色模型进行建模, 然后利用已建立的模型预报第二天相应时间的钟差, 对预报得到的钟差进行拉格朗日插值建模, 通过内插得到其他时刻的预报值, 以此来提高模型的预报能力.文献[11]分析了灰色模型发展系数和灰作用量对预报精度的影响, 之后通过微调这两个参数来提高灰色模型的预报性能, 但是针对钟差数据序列呈现出不同变化趋势时, 没有给出有效的参数优化方法.
从以上的分析可知, 研究者们主要是在优化灰色模型的两个参数方面对模型进行改进, 没有从灰色模型的一次累加生成序列的预报模型方面进行其他处理.基于此, 本文提出了一种基于粒子群算法优化指数函数和线性函数逼近加权灰色回归组合的自适应卫星钟差预报方法.在建模之前, 考虑到卫星钟差钟跳频繁的现象, 首先采用中位数法对卫星钟差进行异常钟差探测, 将异常钟差剔除后采用分段线性插值法将缺失的钟差补齐.然后考虑到卫星钟差存在系统噪声, 采用三点平滑法对钟差数据进行平滑处理后建立了粒子群算法优化指数函数和线性函数逼近加权灰色回归组合的自适应卫星钟差预报模型, 并结合4种典型变化趋势的卫星钟差序列, 采用IGS服务器上发布的事后精密卫星钟差产品作为试验数据, 进行了预报试验.
1 卫星钟差数据预处理 1.1 卫星钟差数据异常探测由于卫星钟差数据跳变频繁, 跳变的钟差数据很不利于建模, 所以在建模之前对卫星钟差数据的质量进行检测就显得很重要.本文采用时效性和抗差性较好的中位数法(Median Absolute Deviation, MAD)进行异常钟差探测[12], 其表达式为
| $ {\rm{MAD}} = {\rm{Median}} \left\{ {\frac{{|{y_i} - {\rm{Median}} ({y_i})|}}{{0.674{\kern 1pt} {\kern 1pt} {\kern 1pt} 5}}} \right\}, $ | (1) |
式中Median(yi)为卫星钟差频率数据yi的中间数.
当卫星钟差的频率yi>(m+n·MAD)或yi < (m+n·MAD)时, 可以判断该点为异常钟差.将探测到的异常钟差剔除后, 采用分段线性插值法把缺失的钟差数据补齐.
1.2 卫星钟差数据平滑性检测由于星载原子钟受自身复杂的时频特性和外界复杂环境的影响, 稳定性存在较大差异的特点, 而卫星钟差是否平滑对于模型的预报性能有很大影响, 所以对观测的钟差进行平滑性检测就显得很有必要.
设原始观测钟差经异常探测补齐后的数据序列为X(1)={x(1)(1), x(1)(2), …, x(1)(n)}, 定义
若ρ(i)满足:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\rho (i + 1)}}{{\rho (i)}} < 1,i = 2,3, \cdots ,n - 1;}\\ {0 < \rho (i) < 0.5,i = 3,4, \cdots ,n - 1.} \end{array}} \right. $ | (2) |
则称钟差数据序列X(1)为平滑序列; 反之, 称钟差数据序列X(1)为非平滑序列.
1.3 三点平滑处理由于卫星钟差数据存在系统噪声, 采用三点平滑法处理, 可以提高卫星钟差数据序列的平滑度.三点平滑法是一种取算术平均的方法, 它通过重新分配待处理的卫星钟差与前后钟差数据的权值, 以加强待处理钟差数据的权重, 从而减小卫星钟差的波动性, 增强待处理的卫星钟差与前后钟差数据间的联系.其过程如下:
设有一组卫星钟差数据序列为
| $ {X^{(1)}} = \{ {x^{(1)}}(1),{x^{(1)}}(2), \cdots ,{x^{(1)}}(n)\} , $ | (3) |
平滑处理位于卫星钟差中间的数据为
| $ \begin{array}{*{20}{c}} {{x^{(2)}}(k) = \frac{{{x^{(1)}}(k - 1) + 2{x^{(1)}}(k) + {x^{(1)}}(k + 1)}}{4},}\\ {k = 2,3, \cdots ,n - 1.} \end{array} $ | (4) |
而对于钟差数据序列两端的数据平滑处理的计算为
| $ \left\{ {\begin{array}{*{20}{l}} {{x^{(2)}}(1) = \frac{{3{x^{(1)}}(1) + {x^{(1)}}(2)}}{4},}\\ {{x^{(2)}}(n) = \frac{{{x^{(1)}}(n - 1) + 3{x^{(1)}}(n)}}{4}.} \end{array}} \right. $ | (5) |
经式(4)和(5)处理后, 得到一组噪声减小的钟差数据序列, 然后建模预报.
2 基于PSO优化的灰色加权回归组合的自适应预报模型 2.1 加权灰色回归组合模型灰色模型是指信息不完全知道的系统, 具体是指它的部分信息是已知的、其余的信息为未知的一种系统.其最常见的灰色系统是GM(1, 1)模型, 它由一个包含单变量的一阶微分方程所构成, 可以实现对自身数据的预测[13].
设X(0)={x(0)(1), x(0)(2), …, x(0)(n)}为不同时刻的卫星钟差, 经过中位数法探测剔除异常钟差数据, 然后采用分段线性插值法把缺失的钟差数据补齐, 得到一组新的钟差数据序列为X(1)={x(1)(1), x(1)(2), …, x(1)(n)}.再使用三点平滑法处理, 以得到一组噪声减小的钟差数据序列为X(2)={x(2)(1), x(2)(2), …, x(2)(n)}, 然后对X(2)这组钟差数据序列建立灰色模型, 则这组数据的一次累加钟差数据序列为X(3)={x(3)(1), x(3)(2), …, x(3)(n)}的灰色预报模型可表示为
| $ \begin{array}{*{20}{l}} {{{\hat x}^{(3)}}(k + 1) = \left[ {{x^{(3)}}(1) - \frac{u}{a}} \right] \cdot {{\rm{e}}^{ - ak}} + \frac{u}{a},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1,2, \cdots ,n - 1.} \end{array} $ | (6) |
记参数为A =[a u]T, 根据最小二乘法可得
| $ \mathit{\boldsymbol{\hat A}} = {\left[ {\begin{array}{*{20}{l}} {\hat a}&{\hat u} \end{array}} \right]^{\rm{T}}} = {({\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}})^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{Y,}} $ | (7) |
式中
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{x^{(3)}}(2)}\\ {{x^{(3)}}(3)}\\ \vdots \\ {{x^{(3)}}(n)} \end{array}} \right],\mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{[{x^{(3)}}(2) + {x^{(3)}}(1)]}}{2}}&1\\ { - \frac{{[{x^{(3)}}(3) + {x^{(3)}}(2)]}}{2}}&1\\ \vdots & \vdots \\ { - \frac{{[{x^{(3)}}(n) + {x^{(3)}}(n - 1)]}}{2}}&1 \end{array}} \right],\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{l}} a\\ u \end{array}} \right]. $ |
将式(7)代入式(6)即可预报出钟差的一次累加序列,然后还原即可得到原始钟差的预报值.
分析可以看出式(6)为以下形式
| $ \begin{array}{*{20}{c}} {{{\hat x}^{(3)}}(k + 1) = {C_1} \cdot {{\rm{e}}^{ - ak}} + {C_2},}\\ {k = 1,2, \cdots ,n - 1.} \end{array} $ | (8) |
由于上式为指数函数和线性函数的叠加形式, 下面采用指数曲线y=aex与线性曲线y=αx+β这两种模型的和来逼近钟差序列X(2)的一次累加生成的序列X(3)的预报值, 如下
| $ {\hat x^{(3)}}(k) = {C_1} \cdot {{\rm{e}}^{vk}} + {C_2}k + {C_3}, $ | (9) |
式中, 参数v和参数C1、C2、C3为待求的参数.
为确定式(9)中的4个未知参数,构造如下序列:
| $ \begin{array}{*{20}{c}} {Z(k) = {{\hat x}^{(3)}}(k + 1) - {{\hat x}^{(3)}}(k)}\\ { = {C_1}{{\rm{e}}^{vk}}({{\rm{e}}^v} - 1) + {C_2},}\\ {k = 1,2, \cdots ,n - 1,} \end{array} $ | (10) |
设:
| $ \begin{array}{*{20}{c}} {{Y_m}(k) = Z(k + m) - Z(k) = }\\ {{C_1}{{\rm{e}}^{vk}}({{\rm{e}}^v} - 1)({{\rm{e}}^{vm}} - 1),}\\ {k = 1,2, \cdots ,n - 1,} \end{array} $ | (11) |
则:
| $ \begin{array}{*{20}{c}} {{Y_m}(k + 1) = Z(k + 1 + m) - Z(k + 1) = }\\ {{C_1}{{\rm{e}}^{v(k + 1)}}({{\rm{e}}^v} - 1)({{\rm{e}}^{vm}} - 1),}\\ {k = 1,2, \cdots ,n - 1,} \end{array} $ | (12) |
用式(12)除以式(11)得:
| $ \frac{{{Y_m}(k + 1)}}{{{Y_m}(k)}} = {{\rm{e}}^v}. $ | (13) |
将式(13)两边取对数得:
| $ v = {\rm{ln}}\left[ {\frac{{{Y_m}(k + 1)}}{{{Y_m}(k)}}} \right]. $ | (14) |
将式(10)中的
当m=1时:
| $ \left\{ {\begin{array}{*{20}{l}} {{Y_1}(k) = Z(k + 1) - Z(k),k = 1,2, \cdots ,n - 2;}\\ {{{\tilde v}_1}(k) = {\rm{ln}}\left[ {\frac{{{Y_1}(k + 1)}}{{{Y_1}(k)}}} \right],k = 1,2, \cdots ,n - 3.} \end{array}} \right. $ | (15) |
当m=2时:
| $ \left\{ {\begin{array}{*{20}{l}} {{Y_2}(k) = Z(k + 2) - Z(k),k = 1,2, \cdots ,n - 3;}\\ {{{\tilde v}_2}(k) = {\rm{ln}}\left[ {\frac{{{Y_2}(k + 1)}}{{{Y_2}(k)}}} \right],k = 1,2, \cdots ,n - 4.} \end{array}} \right. $ | (16) |
直到当m=n-3时:
| $ \left\{ {\begin{array}{*{20}{l}} {{Y_{n - 3}}(k) = Z(n + k - 3) - Z(k),k = 1,2}\\ {{{\tilde v}_{n - 3}}(k) = {\rm{ln}}\left[ {\frac{{{Y_{n - 3}}(k + 1)}}{{{Y_{n - 3}}(k)}}} \right],k = 1.} \end{array}} \right. $ | (17) |
由式(15)~(17)可得
| $ \hat v = \frac{{2\sum\limits_{m = 1}^{n - 3} {\sum\limits_{k = 1}^{n - 2 - m} {{{\tilde v}_m}} } (k)}}{{{n^2} - 5n + 6}}. $ | (18) |
将估计出的
| $ {\hat x^{(3)}}(k) = {C_1}{{\rm{e}}^{\hat vk}} + {C_2}k + {C_3}. $ | (19) |
由于离预报值近一点的钟差对预报的钟差影响大一点, 离预报值远一点的钟差对预报的钟差影响小一点, 下面采用变权加权法来解式(19).变权加权法相对于普通加权法最大的不同是, 变权加权法对钟差时间序列的可靠性成比例的分别赋予不同的权值[14], 具体加权方法如下:
| $ {P_k} = {R^{i - 1}},i = 1,2, \cdots ,n. $ | (20) |
综合式(19)和式(20), 利用最小二乘法可得
| $ \mathit{\boldsymbol{\hat C}} = {\left[ {\begin{array}{*{20}{c}} {{{\hat C}_1}}&{{{\hat C}_2}}&{{{\hat C}_3}} \end{array}} \right]^{\rm{T}}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{X}}^{(3)}}, $ | (21) |
式中
| $ {\mathit{\boldsymbol{X}}^{(3)}} = \left[ {\begin{array}{*{20}{c}} {{x^{(3)}}(1)}\\ {{x^{(3)}}(2)}\\ \vdots \\ {{x^{(3)}}(n)} \end{array}} \right],\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{\hat v}}}&1&1\\ {{{\rm{e}}^{2\hat v}}}&2&1\\ \vdots & \vdots & \vdots \\ {{{\rm{e}}^{n\hat v}}}&n&1 \end{array}} \right],\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{R^0}}&0& \cdots &0\\ 0&{{R^1}}& \cdots &0\\ 0&0& \ddots &0\\ 0&0&0&{{R^n}} \end{array}} \right]. $ |
将式(21)计算出的
精度递增因子R的选取是该算法预报性能好坏的关键, 本文采用粒子群优化算法(Particle Swarm Optimization, PSO)对精度递增因子R进行自适应寻优.
2.2 自适应精度递增因子的求解算法PSO算法是由美国两位科学家受鸟类群体寻找食物的行为得到启发而提出的一种智能优化算法.因为PSO算法收敛速度比较快, 调整参数简单, 所以得到了广泛的应用.因此, 本文选用PSO算法对上述精度递增因子R进行自适应寻优, PSO算法原理[15]如下:
假设在一个目标搜索空间, 其维数为D维且有N个粒子组成一个群落, 其中第i个粒子可表示为一个D维向量
| $ {\mathit{\boldsymbol{X}}_i} = ({x_{i1}},{x_{i2}}, \cdots ,{x_{iD}}),i = 1,2, \cdots ,N. $ | (22) |
第i个粒子的“飞行”速度也是一个D维向量, 记为
| $ {\mathit{\boldsymbol{V}}_i} = ({v_{i1}},{v_{i2}}, \cdots ,{v_{iD}}),i = 1,2, \cdots ,N. $ | (23) |
第i个粒子迄今为止搜索到的最优位置称为个体极值, 记为
| $ {\mathit{\boldsymbol{p}}_{{\rm{ best }}}} = ({p_{i1}},{p_{i2}}, \cdots ,{p_{iD}}),i = 1,2, \cdots ,N. $ | (24) |
整个粒子群迄今为止搜索到的最优位置为全局最优值, 记为
| $ {\mathit{\boldsymbol{g}}_{{\rm{ best }}}} = ({p_{{\rm{g1}}}},{p_{{\rm{g2}}}}, \cdots ,{p_{{\rm{g}}D}}). $ | (25) |
在未找到这两个最优值时, 粒子根据如下的公式来更新自己的速度和位置:
| $ \left\{ \begin{array}{l} {v_{id}}(t + 1) = {w_i}{v_{id}}(t) + {c_1}{r_1}[{p_{id}} - {x_{id}}(t)] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2}{r_2}[{p_{gd}} - {x_{id}}(t)],\\ {x_{id}}(t + 1) = {x_{id}}(t) + {v_{id}}(t + 1),\\ {w_i} = {w_{{\rm{max}}}} - \frac{{({w_{{\rm{max}}}} - {w_{{\rm{min}}}}) \cdot {G_i}}}{{{G_{{\rm{max}}}}}}. \end{array} \right. $ | (26) |
式中:c1和c2为加速常数, 一般取c1=c2=2;r1和r2为[0, 1]范围内的均匀随机数; wi为惯性权重, wmax和wmin为预先确定的最大和最小惯性权重, 一般wmax取0.9, wmin取0.1;Gmax为最大迭代次数; Gi为当前迭代次数.
采用PSO算法对精度递增因子R进行自适应寻优的具体步骤如下:
1) 初始化粒子群的速度、位置、种群规模、最大迭代次数、最大最小惯性权重、训练样本数m和加速常数, 同时定义粒子群的适应度函数为
| $ {f_i} = \sqrt {\frac{{\sum\limits_{i = 1}^m {{{({y_i} - {y_{ip}})}^2}} }}{m}} , $ | (27) |
式中:yi为预报的钟差, yip为实际的观测钟差.
2) 计算各粒子的适应度函数值fi, 然后再比较它们的适应度函数值fi的大小.如果粒子的当前适应度值fi小于该粒子的历史最优适应度值fibest, 则把fibest赋给fi; 同理若fibest小于当前粒子种群的最优适应度值fgbest, 则把fgbest赋给fibest.
3) 根据式(26)更新粒子的速度、位置和惯性权重, 然后判断是否达到了最大迭代次数Gmax.若达到, 则迭代结束, 所得到的最优位置即为精度递增因子R的值; 若未达到, 则继续迭代直到迭代结束.此算法的具体流程见图 1.
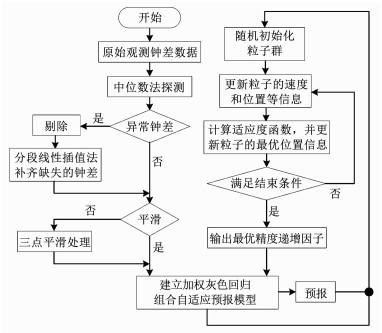
|
图 1 粒子群优化加权灰色回归组合自适应预报算法流程 Fig. 1 Flow chart of the proposed adaptive prediction algorithm |
为了验证本文预报方法的有效性和可行性, 采用IGS服务器(ftp://igs.ign.fr/pub/igs/)上发布的GPS 2 000周, 间隔时长为15 min的SP3格式的事后精密卫星钟差数据进行预报试验.在该时间段内在轨的GPS卫星有31颗, 其星载原子钟有BLOCK IIR-Rb钟、BLOCK IIR-M-Rb钟、BLOCK IIF-Rb钟和BLOCK IIF-Cs四种类型.由于北斗卫星导航系统的星载钟与GPS基本一致, 且北斗二代卫星导航系统均搭载的为铷原子钟, 为使研究结果能为我国北斗卫星导航系统在钟差预报方面提供一些参考, 所以选取了GPS IIF-Rb PRN03、GPS IIR-M-Rb PRN12、GPS IIR-Rb PRN14和GPS IIR-M-Rb PRN17四颗搭载铷原子钟的卫星的钟差数据进行预报试验.截止2019年10月16日, 它们的相关信息见表 1.
| 表 1 选择的卫星相关信息 Tab. 1 Information of the selected satellites |
这四颗卫星第2 000周第0 d的事后精密钟差时间序列的变化情况如图 2所示, 其中PRN03号卫星的钟差时间序列呈正值单调递增趋势, PRN12号卫星的钟差时间序列呈正值单调递减趋势, PRN14号卫星的钟差时间序列呈负值递减趋势, PRN17号卫星的钟差时间序列呈负值单调递增趋势, 具有充分的代表性.
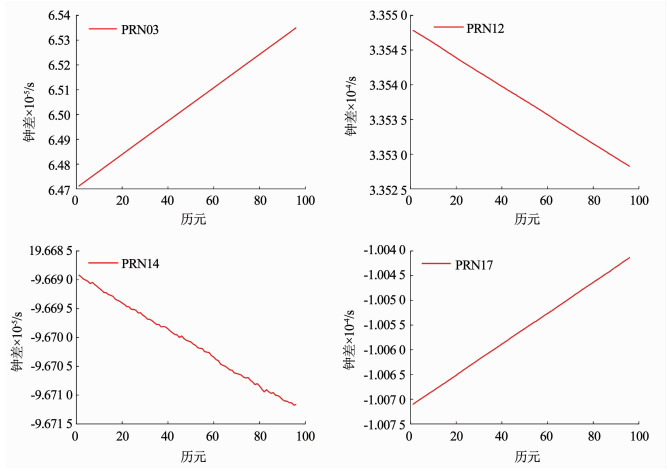
|
图 2 原始观测卫星钟差变化趋势 Fig. 2 Original observation of SCB trends |
由于卫星钟差的有效位数比较多,使得原始观测钟差数据异常点容易被掩盖, 而异常钟差在其对应的频率数据中表现为显著的峰值点, 所以先将卫星钟差转换为相应的频率数据后更容易对异常钟差进行探测, 具体转换公式如下
| $ {y_i} = \frac{{{x_{i + 1}} - {x_i}}}{{{\tau _0}}}, $ | (28) |
式中:yi表示卫星钟差的频率数据, xi+1和xi分别表示第i+1和i历元的卫星钟差值(相位数据), τ0表示采样间隔.
PRN03、PRN12、PRN14和PRN17号卫星相应的频率数据变化见图 3, 经中位数法探测发现, 在此时间段内, PRN03、PRN14和PRN17三颗卫星存在异常的钟差数据, 将探测的异常钟差数据剔除后采用分段线性插值法将缺失的数据补齐, 补齐后的变化见图 4, 然后还原为钟差的相位数据进行建模预报.
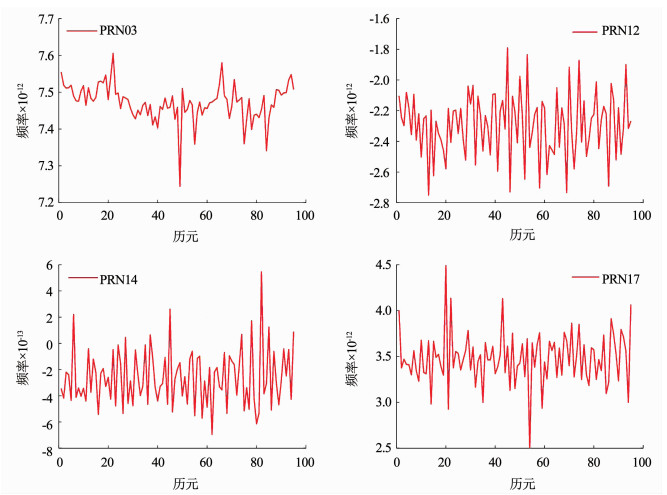
|
图 3 原始观测卫星钟差的频率变化 Fig. 3 Frequency variation of original SCB data |
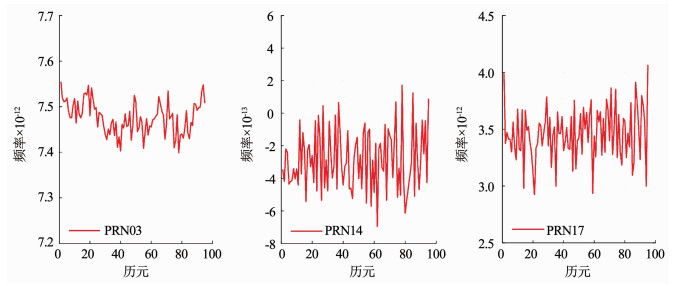
|
图 4 剔除异常钟差补齐后的频率数据 Fig. 4 Frequency variation after removing and making up abnormal clock bias data |
IGS发布的超快速卫星星历产品的更新时间约为6 h, 鉴于此, 为了验证本文所提方法对卫星钟差预报的优势, 分别建立了二次多项式模型(QPM)、灰色模型(GM(1, 1))、修正指数曲线法模型(MECM)、自回归滑动平均模型(ARMA)和本文的预报模型(New method), 对未来6 h的卫星钟差进行预报试验, 并且将本文预报模型预报的结果同其他各模型预报的结果进行比较分析.评价模型预报性能的好坏, 采用均方根误差RMS(计算公式见式(29))和最大误差与最小误差之差的绝对值, 即极差Range(计算公式见式(30))作为评价预报结果的统计量, 去比较分析各模型的预报精度及其稳定度.其中RMS表征了预报结果的精度, Range表征了算法的稳定度.
| $ {\rm{RMS}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{({\rm{ error}}{{\rm{ }}^{(i)}})}^2}} }}{n}} , $ | (29) |
| $ {\rm{Range}} = | {\rm{error}}_{{\rm{max}}}^{(i)} - {\rm{error}}_{{\rm{min}}}^{(i)} |. $ | (30) |
式中:error(i)=
|
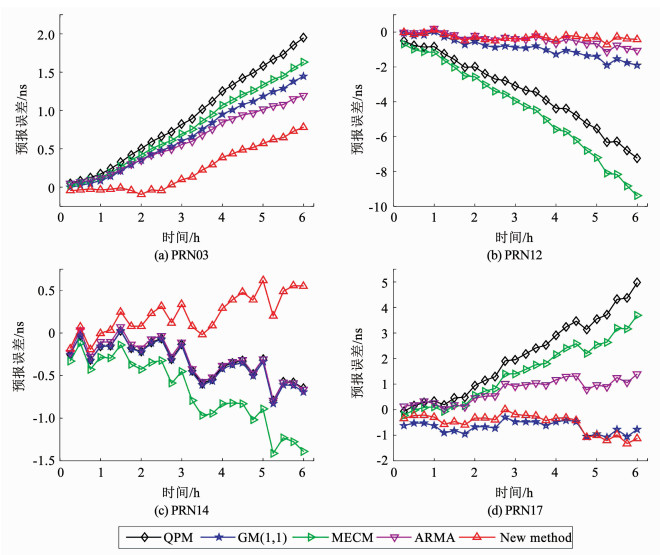
图 5 6 h预报误差对比 Fig. 5 Comparison of 6-h forecast errors of different models |
|
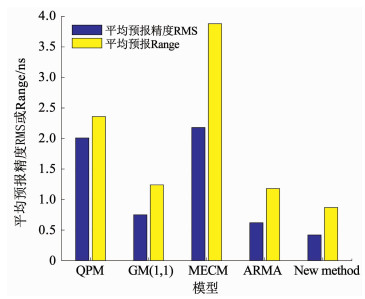
图 6 平均预报精度RMS、算法稳定度Range统计对比 Fig. 6 Comparison of RMS and Range values of different models |
| 表 2 卫星钟差预报误差统计 Tab. 2 Statistics of SCB prediction errors |
图 5为5种模型的预报误差变化图, 图 6为5种模型的平均预报精度RMS和算法稳定度Range的统计图,表 2为5种模型的预报误差的统计结果, 由图 5~6和表 2可知:
1) 在卫星钟差6 h的预报中, 本文提出的新方法预报精度最高.无论是对于早期发射的IIR型卫星, 还是最近几年发射的IIF型卫星, 均可以达到亚纳秒级的预报精度, 可以实现厘米级的定位.算法的稳定度也均小于其他预报模型, 具有较高的预报稳定性.
2) 在卫星钟差6 h的预报中, MECM预报模型的预报性能最差, 平均预报精度达到了2.18 ns, 平均算法稳定度达到了3.88 ns, 这进一步说明了MECM模型比较适合于类指数变化趋势的卫星钟差预报, 而不适合大致呈单调递增或者单调递减的卫星钟差的预报; 其次是QPM模型, 平均预报精度为2.01 ns, 平均算法稳定度为2.36 ns; 而GM(1, 1)模型和ARMA模型的预报性能大致相当, 其平均预报精度分别为0.75 ns和0.62 ns, 平均算法稳定度分别为1.24 ns和1.18 ns.
3) 粒子群优化加权灰色回归组合的自适应卫星钟差预报模型的精度明显优于其他4种模型, 6 h的平均预报精度为0.42 ns, 平均算法稳定度为0.87 ns, 相对于目前正在卫星上使用的二次多项式模型的平均预报精度提高了79.10%, 平均算法稳定度提高了63.10%.
4) 采用本文的预报方法, 四颗星载钟的预报精度均达到了亚纳秒量级的预报精度.由于星载钟受发射时间的长短、设备老化、钟差变化趋势以及所处环境等复杂因素的影响, 所以预报误差存在一定程度上的差异.
4 结论本文提出的粒子群算法优化指数函数和线性函数逼近加权灰色回归组合的自适应卫星钟差预报模型, 在建模之前先对钟差的质量进行检测, 剔除异常钟差数据用分段线性插值法将缺失的钟差数据补齐, 然后进行平滑性检测, 对于非平滑序列进行平滑处理, 之后用指数函数和线性函数去逼近灰色模型的一次累加序列后, 采用变权加权法进行组合预报.针对精度递增因子难以确定的问题, 引入了粒子群优化算法进行自适应寻优最佳的精度递增因子, 最后进行了6 h的钟差预报.在6 h的钟差预报中, 所提方法的平均预报精度和平均算法稳定度均可以达到亚纳秒量级, 能够满足精密单点定位对卫星钟差精度的要求, 为卫星钟差预报提供了一种新的方案, 但是该方法仍然没有克服误差累积的现象, 所以还有待进一步研究如何实现卫星钟差高精度的预报.
| [1] |
于烨, 张慧君, 李孝辉. 顾及钟差随机项的GPS卫星钟差预报[J]. 测绘通报, 2018(6): 1. YU Ye, ZHANG Huijun, LI Xiaohui. GPS satellite clock bias prediction method considering random items of clock bias[J]. Bulletin of Surveying and Mapping, 2018(6): 1. DOI:10.13474/j.cnki.11-2246.2018.0166 |
| [2] |
WANG Yupu, LU Zhiping, QU Yunying, et al. Improving prediction performance of GPS satellite clock bias based on wavelet neural network[J]. GPS Solutions, 2016, 21(2): 523. DOI:10.1007/s10291-016-0543-z |
| [3] |
李源, 战兴群, 梅浩, 等. 灰色粒子群自适应卫星钟差预报方法[J]. 哈尔滨工业大学学报, 2018, 50(4): 71. LI Yuan, ZHAN Xingqun, MEI Hao, et al. Particle swarm adaptive satellite clock error prediction model based on grey theory[J]. Journal of Harbin Institute of Technology, 2018, 50(4): 71. DOI:10.11918/j.issn.0367-6234.201610027 |
| [4] |
刘赞, 陈西宏, 孙际哲, 等. 改进粒子群算法优化的卫星钟差组合预报模型[J]. 探测与控制学报, 2015, 37(1): 94. LIU Zan, CHEN Xihong, SUN Jizhe, et al. Combined prediction model of satellite clock error optimized by IPSO[J]. Journal of Detection & Control, 2015, 37(1): 94. |
| [5] |
于烨, 黄默, 杨斌, 等. 一种高精度导航卫星钟差中长期预报方法[J]. 仪器仪表学报, 2019, 40(9): 36. YU Ye, HUANG Mo, YANG Bin, et al. A high-precision medium-long term prediction method for navigation satellite clock bias[J]. Chinese Journal of Scientific Instrument, 2019, 40(9): 36. DOI:10.19650/j.cnki.cjsi.J1905250 |
| [6] |
WANG Dongxia, GUO Rui, XIAO Shenghong, et al. Atomic clock performance and combined clock error prediction for the new generation of BeiDou navigation satellites[J]. Advances in Space Research, 2019, 63(9): 2889. DOI:10.1016/j.asr.2018.01.020 |
| [7] |
于烨, 张慧君, 李孝辉. 基于一阶差分修正指数曲线法的GPS卫星钟差预报[J]. 探测与控制学报, 2018, 40(4): 94. YU Ye, ZHANG Huijun, LI Xiaohui. GPS satellite clock bias prediction based on first-order difference MECM[J]. Journal of Detection & Control, 2018, 40(4): 94. |
| [8] |
于烨, 黄默, 王小青, 等. 利用最小一乘法改进的灰色模型的导航卫星钟差预报[J]. 测绘通报, 2019(4): 1. YU Ye, HUANG Mo, WANG Xiaoqing, et al. Navigation satellite clock bias prediction based on grey model improved by least absolute deviations[J]. Bulletin of Surveying and Mapping, 2019(4): 1. DOI:10.13474/j.cnki.11-2246.2019.0102 |
| [9] |
李成龙, 陈西宏, 刘继业, 等. 利用自适应TS-IPSO优化的灰色系统预报卫星钟差[J]. 武汉大学学报(信息科学版), 2018, 43(6): 854. LI Chenglong, CHEN Xihong, LIU Jiye, et al. Predicting satellite clock errors using grey model optimized by adaptive TS-IPSO[J]. Geomatics and Information Science of Wuhan University, 2018, 43(6): 854. DOI:10.13203/j.whugis20160101 |
| [10] |
石宁, 卢辰龙, 杨登科, 等. 基于拉格朗日插值的灰色模型卫星钟差预报[J]. 测绘技术装备, 2018, 20(4): 5. SHI Ning, LU Chenlong, YANG Dengke, et al. Grey model satellite clock error prediction based on Lagrange interpolation[J]. Geomatics Technology and Equipment, 2018, 20(4): 5. DOI:10.3969/j.issn.1674-4950.2018.04.002 |
| [11] |
路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2008, 33(5): 492. LU Xiaofeng, YANG Zhiqiang, JIA Xiaolin, et al. Parameter optimization method of gray system theory for the satellite clock error predicating[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 492. |
| [12] |
蔡成林, 何成文, 韦照川. 一种GPS ⅡR-M型卫星超快星历钟差预报的高精度修正方法[J]. 测绘学报, 2016, 45(7): 782. CAI Chenglin, HE Chengwen, WEI Zhaochuan. A high-precision correction method of ultra-rapid ephemeris clock bias prediction for GPS block ⅡR-M satellites[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 782. DOI:10.11947/j.AGCS.2016.20160017 |
| [13] |
于烨, 张慧君, 李孝辉. 含误差预报校正的GM(1, 1)卫星钟差预报新方法[J]. 测绘科学, 2019, 44(4): 8. YU Ye, ZHANG Huijun, LI Xiaohui. A new method of GM(1, 1) satellite clock bias prediction with error prediction correction[J]. Science of Surveying and Mapping, 2019, 44(4): 8. DOI:10.16251/j.cnki.1009-2307.2019.04.002 |
| [14] |
韩晓东, 贺兆礼. 灰色GM(1, 1)与线性回归组合模型及其在变形预测中的应用[J]. 淮南矿业学院学报, 1997, 17(4): 51. HAN Xiaodong, HE Zhaoli. Combination model of GM(1, 1) and linear regression and its application in deformation prediction[J]. Journal of Huainan Mining Institute, 1997, 17(4): 51. |
| [15] |
刘强, 孙际哲, 陈西宏, 等. CPSO-LSSVM在自回归钟差预报中的应用[J]. 吉林大学学报(工学版), 2014, 44(3): 807. LIU Qiang, SUN Jizhe, CHEN Xihong, et al. Application analysis of CPSO-LSSVM algorithm in AR clock error prediction[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 807. DOI:10.13229/j.cnki.jdxbgxb201403036 |
 2020, Vol. 52
2020, Vol. 52


