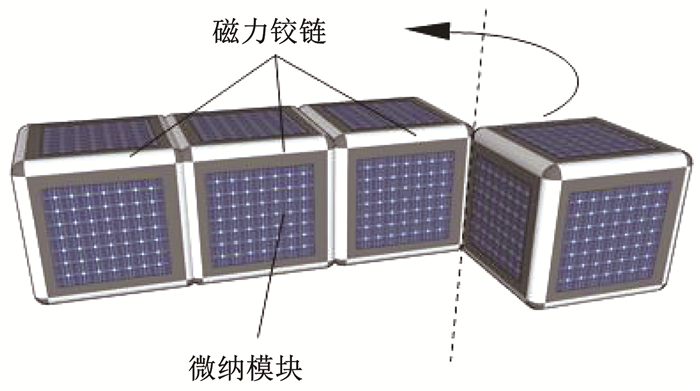
微纳聚合体卫星是由多个立方体微纳模块通过磁力铰链机构相互吸附而形成的组合体航天器.磁力铰链机构分布于各模块的12条棱上，微纳模块在磁力铰链的约束下以棱为转轴进行转动，从而实现微纳聚合体卫星的构型重构.图 1为变构过程的原理示意图.

构型可重构的模块化航天器由于具有较强的可扩展性、适应性，可满足不同的任务需求，近年来引起了各国研究人员的关注.日本开展了板块延展卫星(panel extension satellite, PETSAT)计划^[1-2]，但卫星面板之间通过机械铰链连接，连接方式在地面确定，无法在轨更改，因而无法实现任意形态的重构.英国萨里大学的可重构太空望远镜自主拼接(autonomous assembly of a reconfigurable space telescope, AAReST)项目，计划通过多颗卫星模块的分离与再拼接实现不同望远镜构型之间的变换，以满足不同的成像需求^[3-4].但分离后再拼接的策略在控制上面临姿轨耦合问题的挑战，姿轨耦合控制也会导致相对较多的燃料消耗.

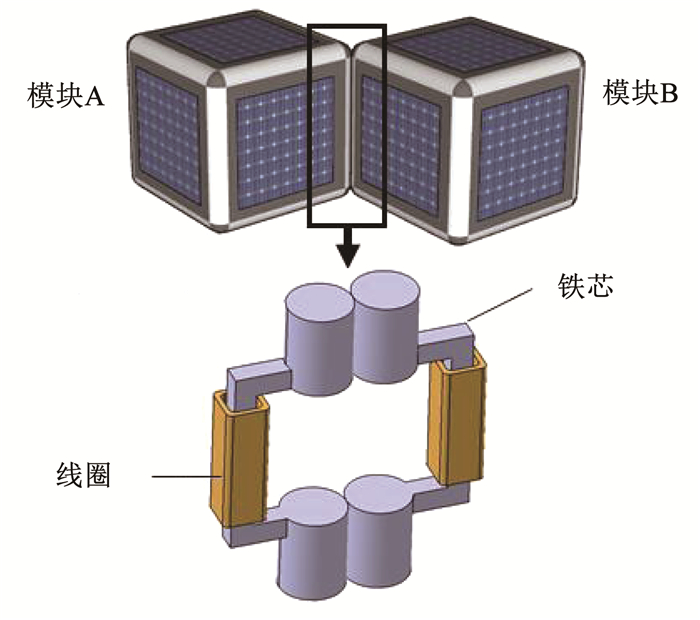
磁力铰链的示意图如图 2所示，基于磁力铰链的微纳聚合体卫星利用了铰链约束的特性，可将微纳模块的转动转化为位置的改变，磁力铰链分布于微纳模块的12条棱上，通过电流的通断决定铰链的吸附与分离，这使得微纳模块可实现在3个方向的转动.这意味着通过不同模块的多次运动可实现任意两构型之间的变换.磁铰链机构在可重构模块化机器人领域已有成功应用^[5-6]，在航天领域有较大潜在应用价值.

在微纳聚合体卫星变构过程中，运动中的模块与组合体中其他部分构成了一个漂浮基多刚体系统，两者在动力学上是耦合的：当某个模块转动时，由于角动量守恒，其余刚体会发生与之方向相反的转动，即某个刚体位置与姿态的变化会影响其他刚体的位置与姿态，且磁铰链处除约束内力与力矩外，还有由磁力导致的主动力与力矩作用于各刚体，对变构过程造成干扰，这给变构过程的柔顺控制带来了挑战.对于漂浮基多刚体系统的控制研究主要集中在空间漂浮基机械臂的控制、空间站舱段转位控制等方面.西北工业大学李磊等^[7]针对空间站舱段转位的场景，设计了全程滑模控制器，对核心舱、功能舱以及空间机械臂各关节都进行了控制，实现了功能舱的转位与核心舱的姿态稳定.但任务需求与控制器特性决定了该控制方法除了对机械臂进行控制外还需为核心舱提供控制力矩.吉林大学赵永佳^[8]利用神经网络的方法对漂浮基空间机械臂进行控制，该方法不需要精确的系统动力学模型，在基座不受控的情况下实现了机械臂的轨迹跟踪，但控制器设计较为复杂.

因此，本文采用一种量化因子在线调节的模糊控制器对微纳聚合体卫星变构过程进行控制，该方法不依赖于系统动力学模型，只需对参与变构的模块进行控制，且控制器的设计基于直观的模糊规则，设计过程简单明了.

1 动力学模型 1.1 运动关系分析

微纳聚合体卫星变构存在多种方式：串行变构和并行变构，前者每次只有一个模块参与变构运动，或者有多个模块同时变构.本文主要研究串行变构下的控制问题，因此，在每一次变构过程中，整个组合体可看作一个两刚体系统，即由参与变构运动的模块(以下称为运动模块)与组合体中的其他部分(以下称为本体)两个刚体组成的系统.

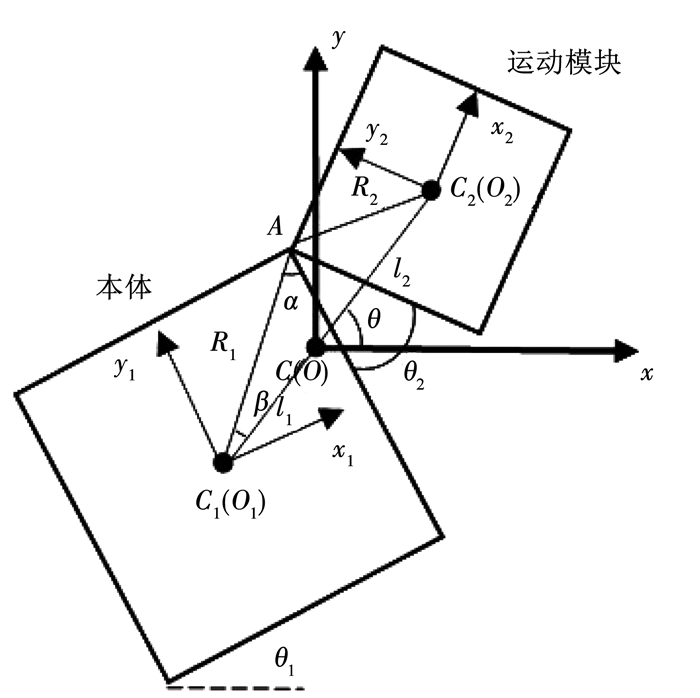
变构时，立方体运动模块绕磁力铰链做一个自由度的转动，则在垂直于转轴的平面上建立一个平动坐标系O-xy，坐标系原点与系统总质心C重合，坐标轴可为平面内任意方向；O₁-x₁y₁与O₂-x₂y₂分别为本体与运动模块的本体系，与O-xy共面，原点分别与两者质心重合，坐标轴分别平行于本体与模块的边线，如图 3所示.忽略重力梯度，在C点，运动引起的惯性力与万有引力平衡，则系统为不受外力的漂浮基多体系统，O-xy可视为惯性基^[9].

C₂为运动模块质心，其到C的距离为l₂，设运动模块质量为m₂，绕惯性主轴(过质心且垂直于O₁-x₂y₂平面)转动的惯量为J₂.本体可等效为一质心为C₁，质量为m₁，绕惯性主轴(过质心且垂直于O₁-x₁y₁平面)转动的惯量为J₁的长方体刚体，C₁到C的距离为l₁.R₁，R₂分别为C₁，C₂到转轴的距离.θ₁为x₁轴相对于x轴的逆时针夹角，θ₂为x₂轴相对于x₁轴的逆时针夹角，即运动模块相对于本体转动的角度.θ为连线C₁C₂与x轴的夹角，β为连线C₁A与C₁O的夹角.由于变构全过程系统不受外力作用，则坐标系O-xy始终可视为惯性系.

由此可得到C₁，C₂位置关系为：

$ {{x_1} = - \frac{{{m_2}}}{{{m_1} + {m_2}}}l\cos \theta ,} $

(1)

$ {{y_1} = - \frac{{{m_2}}}{{{m_1} + {m_2}}}l\sin \theta ,} $

(2)

$ {{x_2} = - \frac{{{m_1}}}{{{m_1} + {m_2}}}l\cos \theta ,} $

(3)

$ {{y_2} = - \frac{{{m_1}}}{{{m_1} + {m_2}}}l\sin \theta ,} $

(4)

式中l，θ由下式所示的几何关系确定：

$ {l = \sqrt {R_1^2 + R_2^2 - 2{R_1}{R_2}\cos ({\theta _2} + \alpha + \frac{{\rm{ \mathsf{ π} }}}{4})} ,} $

(5)

$ {\theta = \frac{{\rm{ \mathsf{ π} }}}{2} + {\theta _1} - \alpha - \beta ,} $

(6)

$ {\frac{{{R_2}}}{{\sin \beta }} = \frac{l}{{\sin (\alpha + {\theta _2} + \frac{{\rm{ \mathsf{ π} }}}{4})}}.} $

(7)

1.2 磁力铰链力学模型

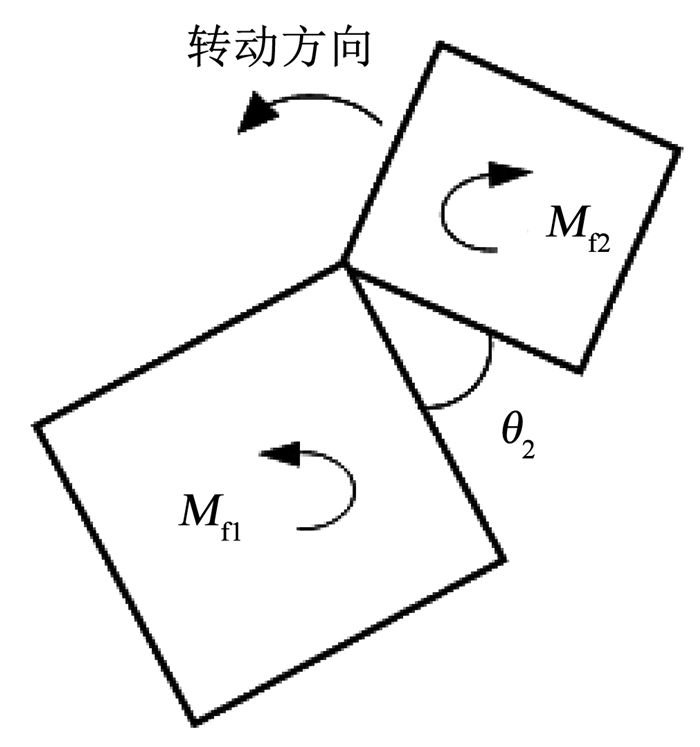
磁力铰链需要提供足够大的磁力以保证变构过程中模块吸附于本体上，因此也会给运动模块的转动带来一定的阻碍，需要在动力学建模和控制中将这一因素纳入考虑.这一阻碍作用表现为一对磁力矩分别作用于运动模块与本体上，如图 4所示.

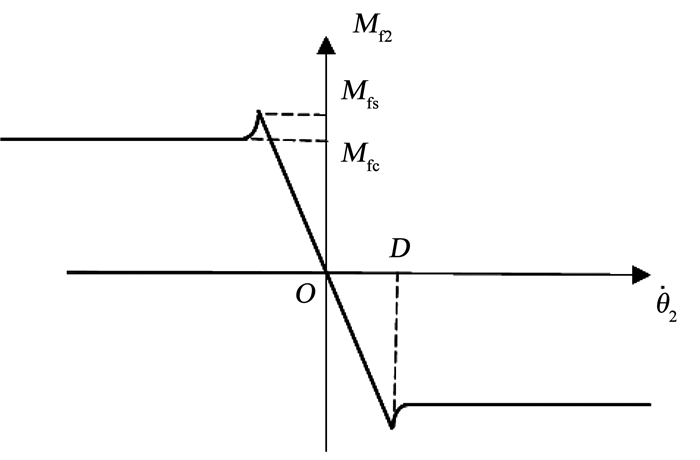
该力矩是由磁力铰链接触面相互挤压导致的形变产生的，与滚动摩擦形成的机理类似，故套用摩擦力的建模方式对其建模.M_f1与M_f2大小相等，方向相反，该力矩的建模采用静摩擦与库伦摩擦模型的近似建模方法^[10-12]，将摩擦力矩在相对运动角速度零点的特性用具有一定斜率的直线线性表示，直线斜率由角速度界限D与最大静摩擦力矩M_fs决定，M_fc为动摩擦力矩，摩擦力矩与相对运动角速度的关系如图 5所示.

1.3 系统动力学方程

采用第2类拉格朗日方程对系统进行动力学建模，由式(1)~(7)可求得本体与运动模块的质心位置，微分可得到两者质心平动速度v₁与v₂，则本体的动能为

$ {E_1} = \frac{1}{2}{m_1}v_1^2 + \frac{1}{2}{J_1}\dot \theta _1^2, $

运动模块的动能为

$ {E_2} = \frac{1}{2}{m_2}v_2^2 + \frac{1}{2}{J_2}{({\dot \theta _1} + {\dot \theta _2})^2}. $

忽略系统重力势能的变化，利用下式拉格朗日方程：

$ {L = {E_1} + {E_2},} $

$ {\frac{d}{{dt}}(\frac{{\partial L}}{{\partial \mathit{\boldsymbol{\dot q}}}}) - \frac{{\partial L}}{{\partial \mathit{\boldsymbol{q}}}} = \mathit{\boldsymbol{Q}} + {\mathit{\boldsymbol{Q}}_{\rm{f}}},} $

可得到如下形式的系统动力学方程：

$ \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} = \mathit{\boldsymbol{\tau }} + {\mathit{\boldsymbol{M}}_{\rm{f}}}. $

(8)

式中，q =[θ₁, θ₂]^T，为广义坐标；τ为控制力矩；M_f为铰链摩擦力矩.

当m₁=m₂=m，J₁=J₂=J，R₁=R₂=R，α=π/4时，式(8)可简化为下式：

$ \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}m{R^2}(1 + \sin {\theta _2}) + 2J}&{\frac{1}{4}m{R^2}(1 + \sin {\theta _2}) + J}\\ {\frac{1}{4}m{R^2}(1 + \sin {\theta _2}) + J}&{\frac{1}{4}m{R^2} + J} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{\ddot \theta }_1}}\\ {{{\ddot \theta }_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}m{R^2}{{\dot \theta }_2}\cos {\theta _2}}&{\frac{1}{4}m{R^2}{{\dot \theta }_2}\cos {\theta _2}}\\ { - \frac{1}{4}m{R^2}{{\dot \theta }_1}\cos {\theta _2}}&{\frac{1}{{16}}m{R^2}{{\dot \theta }_2}\cos {\theta _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \theta }_1}}\\ {{{\dot \theta }_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\tau _1}}\\ {{\tau _2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{M_{{\rm{f1}}}}}\\ {{M_{{\rm{f2}}}}} \end{array}} \right]. $

(9)

2 控制器设计 2.1 控制方法的选择

由方程(9)可知，运动模块与本体之间动力学高度耦合，作用于运动模块和本体上的力矩都会对两者的姿态同时产生影响.因此，对于在设计过程中依赖于系统动力学模型的控制方法来说，要想实现变构过程的控制，需要同时对本体和模块作用控制力矩，即两者的动量轮均需要工作.对于单纯的变构这一过程，对本体的姿态控制是不必要的，这会带来更多的能量消耗，因此，需要一种不依赖于精确的系统动力学模型，仅在运动模块上作用一个控制力矩就可以完成变构控制的方法，而模糊控制满足该要求.

模糊控制利用模糊集合理论，模拟人的思维方式对被控对象进行有效控制.因此，该控制方法不依赖于系统动力学模型^[13-14]，只需获取误差与误差变化率等信息，并可通过调节量化因子等参数改善控制效果，达到柔顺控制的目的.因此，本文采用模糊控制的方法对变构过程进行控制.

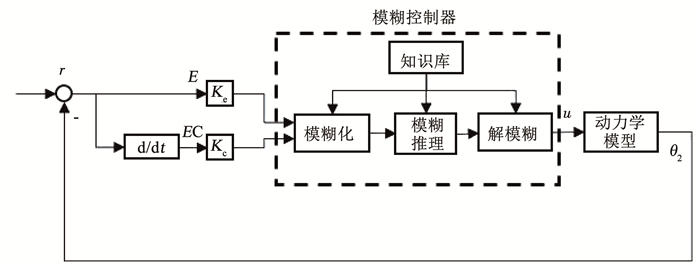
2.2 组合体变构模糊控制器

变构控制采用的模糊控制器的基本框架如图 6所示.

组合体变构时，运动模块转动的角度为90°或180°，故将模块控制器输入量设置为误差E=π－θ₂和误差变化率$E C=-\dot{\theta}_{2}$，输出量为控制力矩u，其语言变量分别用E，EC和U表示，三者的论域分别为[0, π] (rad)，[-0.16, 0.16] (rad/s)以及[-0.08, 0.08] (N·m).EC与U论域根据实际情况设定，考虑到变构过程的柔顺以及执行机构的能力，EC与U的论域不应过大.则模糊语言变量设定如下：

$ {A = \{ {\rm{ZE,S,M,B}}\} ,} $

$ {B = \{ {\rm{NB,NM,NS,ZE,PS,PM,PB}}\} ,} $

$ {C = \{ {\rm{NB,NM,NS,ZE,PS,PM,PB}}\} .} $

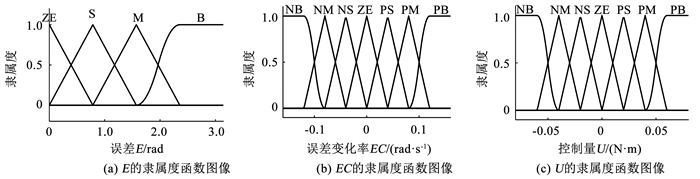
式中：S、M、B分别为小、中、大；NB、NM、NS、ZE、PS、PM、PB分别为负大、负中、负小、零、正小、正中、正大.三者的隶属度函数如图 7(a)~图 7(c)所示.

模糊控制规则基于以下几条原则进行设计：

1) 误差E较大时，提供较大正向控制力矩或较小负向控制力矩；

2) 误差变化率EC为负且较大时，提供较小的正向控制力矩或较大负向控制力矩，EC为正且较大时，提供较大正向控制力矩或较小负向控制力矩；

3) 由于铰链摩擦的阻碍作用，E极小且EC极小时，适当正向增大控制力矩.

模糊规则表见表 1.对上述的模糊控制器采用min-max模糊推理方法，并利用重心法实现解模糊.

2.3 量化因子模糊调节器

为改善控制系统的动态特性，达到柔顺变构的效果，需要对量化因子K_e与K_c进行在线的调节.量化因子K_e与K_c对系统的动态性能的影响主要表现为：K_e越大，系统输出的上升速率越大，调节时间越长，会产生更大的超调；K_c越大，响应速度越慢，调节时间越短，超调量越大^[15].

将θ₂由0变化到30°的阶段定义为起动段，将θ₂达到150°之后的阶段定义为末段.柔顺控制主要关注的是这两个阶段，则变构过程的“柔顺”主要包含以下几点含义：

1) 在起动段与末段，$ \dot{\theta}_{2}$变化较平缓，角速度突变情况较少；

2) 超调量小，变构完成的瞬间$ \dot{\theta}_{2}$的值尽可能接近于0，即减小模块与本体之间的碰撞冲击.

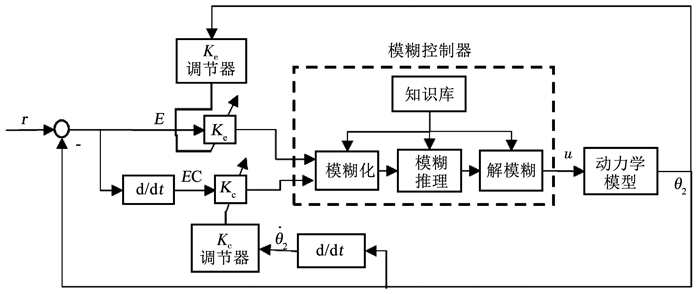
基于以上要求，量化因子调节器的调节规则如下，改进后控制系统的框架如图 8所示.

1) 起动段.随着θ₂的增大，K_e增大，随着$\left| {{{\dot \theta }_2}} \right|$的增大，K_c减小.

2) 末段.随着θ₂的增大，K_e减小，随着$\left| {{{\dot \theta }_2}} \right|$的增大，K_c减小.

3) 末段的K_c相对于起动段的K_e较小.

4) 其他阶段.量化因子为定值.

设θ₂、$\left| {{{\dot \theta }_2}} \right|$、K_e、K_c的语言变量分别为THETA、DTHETA、KE、KC，则：

$ {{\rm{THETA}} = \{ {\rm{S,M,B}}\} ,} $

$ {{\rm{DTHETA}} = \{ {\rm{ZE,S,M,B}}\} ,} $

$ {KE = \{ {\rm{S,M,B}}\} ,} $

$ {KC = \{ {\rm{S,M,B}}\} .} $

θ₂在起动段的论域为[0, π/6](rad)，在末段的论域为[5π/6, π](rad)，$\left| {{{\dot \theta }_2}} \right|$的论域为[0, 0.1] (rad/s)，K_e的论域均为(0, 2]，K_c在起动段的论域为(0, 4]，在末段的论域为(0, 3].四者的隶属度函数均为与图 7类似的三角型隶属度函数.则起动段与末段的量化因子调节规则见表 2~4.

3 数学仿真

图 3中标注的各几何参数以及其他仿真参数设置见表 5.

模糊推理方法仍为min-max方法，解模糊方法仍为重心法.

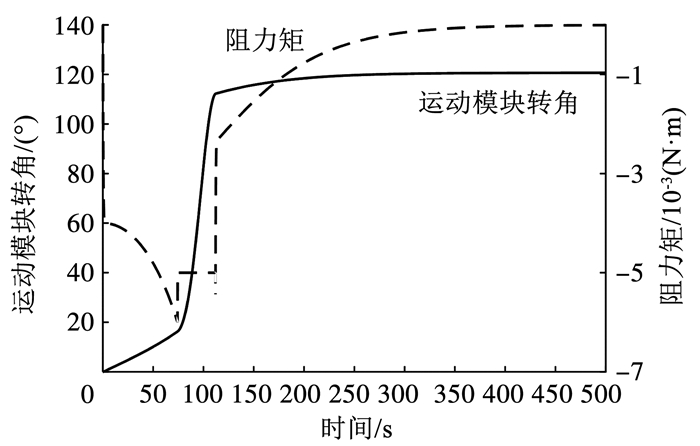
首先要验证磁力铰链摩擦对变构的影响，仿真初始条件为θ₁=0 rad，θ₂=0 rad，${{\dot \theta }_1}{\rm{ = }}0$ rad/s，${{\dot \theta }_2}{\rm{ = }}0$rad/s，θ₂目标值为180°，且达到180°后保持不变.作用于运动模块的控制力矩τ₂为一定值，由仿真可知：当其大小与铰链最大静摩擦力矩M_fs为同一量级(此处设置为0.006 N·m)时，运动模块转动受到阻碍，本体与运动模块最终以相同角速度同步转动.运动模块转角θ₂随时间变化的曲线以及运动模块所受铰链阻力矩M_f2的变化如图 9所示.

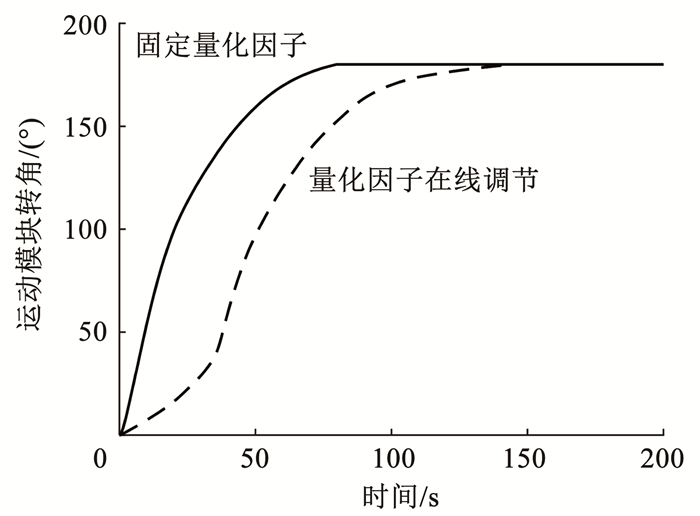
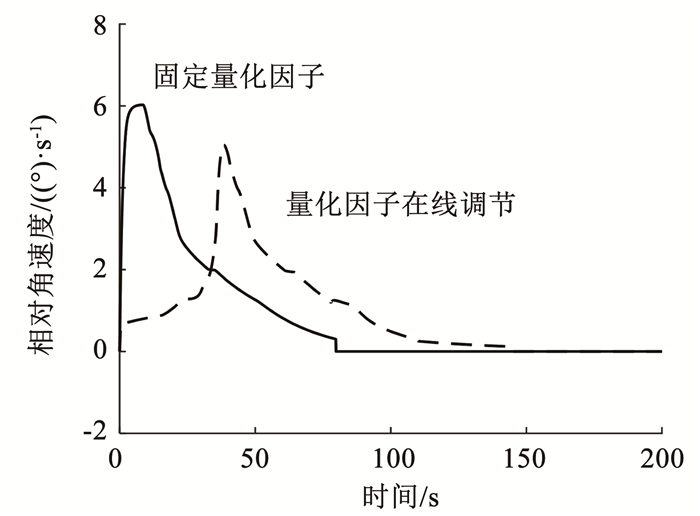
其次验证变构控制方法的有效性，仿真初始条件同上，分别对量化因子恒为1和量化因子在线调节两种情况下的变构过程进行仿真，得到的运动模块转角θ₂和模块相对于本体角速度${{\dot \theta }_2}$随时间的变化曲线如图 10、11所示.

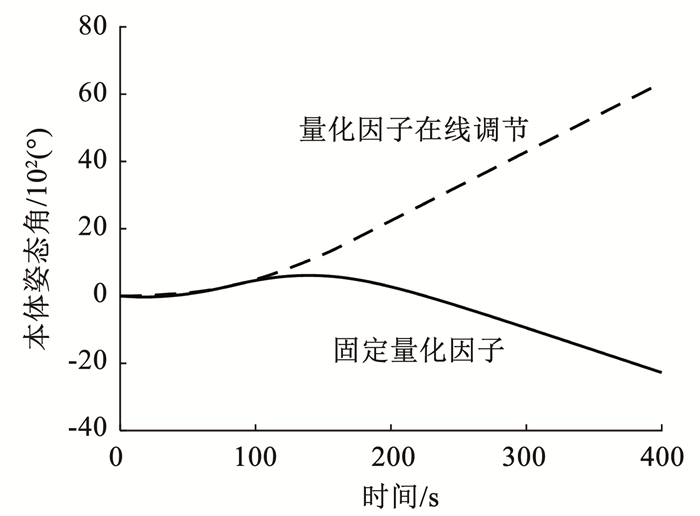
量化因子恒为1和量化因子在线调节两种情况下本体姿态角θ₁变化曲线如图 12所示.

由图 10、11仿真结果可知，所设计的控制器能输出足够大的控制力矩以抵抗磁力矩的阻碍，且量化因子在线调节的控制中，相对角速度变化相比于固定量化因子的控制更平缓.由图 12可知，两种控制方法下，本体姿态在变构结束后均线性变化，即本体匀速转动，但量化因子在线调节情况下，变构结束前θ₁正向增加，说明本体角速度与模块转动同向，再次表明两者相对角速度较小，碰撞冲击较小.为了量化变构过程的柔顺程度，引入以下两个评价参数：

1) 起动段模块相对于本体的角加速度绝对值的平均值，记为α_start；

2) 变构完成瞬间(即θ₂首次达到180°瞬间时刻)模块相对于本体的角速度大小，记为ω_end.

变构开始后首次角速度数据采集时刻记为t₁，起动段结束前最后一次角速度数据采集时刻记为t_M，变构结束前最后一次角速度数据采集时刻记为t_N(M，N为正整数)，采样间隔为Δt，则α_start与ω_end根据以下公式确定：

$ {{{\bar \alpha }_{{\rm{ start }}}} = \frac{1}{{M - 1}}\sum\limits_{i = 1}^{M - 1} {\frac{{|{{\dot \theta }_2}({t_{i + 1}}) - {{\dot \theta }_2}({t_i})|}}{{\Delta t}}} ,} $

(10)

$ {{\omega _{{\rm{ end }}}} = {{\dot \theta }_2}({t_N}).} $

(11)

式(10)反映了相对角速度变化的平缓程度，式(11)反映了变构完成时运动模块与本体碰撞的冲击程度.两个指标在采用固定量化因子和在线调节量化因子两种控制方法下的值见表 6.

由表 6可知，量化因子在线调节的控制方法中两个指标均低于固定量化因子的方法，说明量化因子在线调节的方法能有效增加变构控制的柔顺程度，达到了控制目标.

4 物理试验验证

为进一步验证控制方法的有效性，在三自由度平面气浮台上进行了物理仿真试验.试验所用的平面气浮台如图 13所示.

如图 13所示，用两个平面气浮台分别模拟变构过程中的本体与运动模块，两者之间由销钉机构的铰链替代磁铰链进行连接.销钉铰链阻力矩来源滑动摩擦，与磁铰链的滚动摩擦在动力学模型形式上相同，均可由图 5所示曲线进行描述.

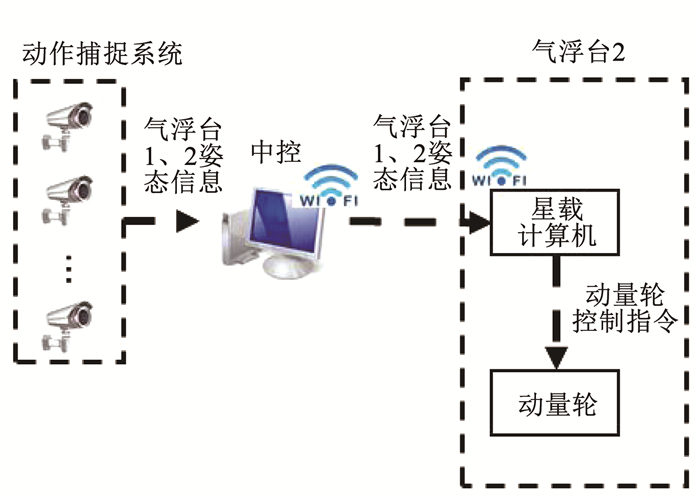
气浮台2上的单轴偏置动量轮提供变构控制所需的力矩，最大输出力矩为0.1 N·m.两个气浮台的姿态信息由动作捕捉系统测量.物理试验方案如图 14所示.

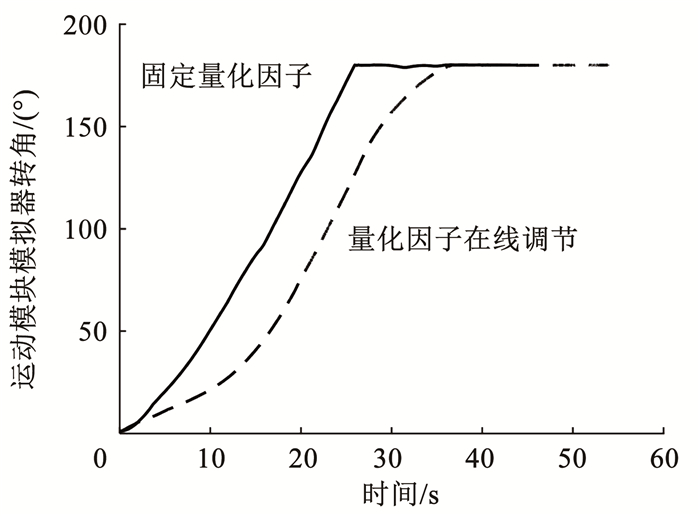
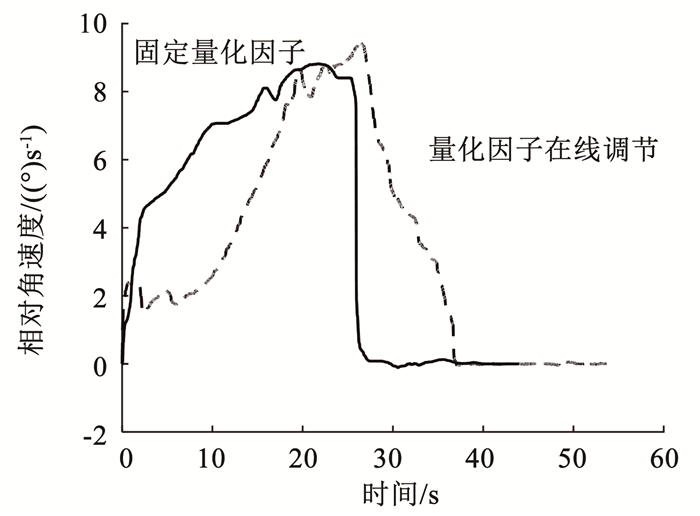
分别对固定量化因子和量化因子在线调节两种方法进行试验，得到的实验结果如图 15、16所示.

仍采用上述的柔顺程度评价参数对实验结果进行评估，则两个指标在两种控制方法下的值见表 7.

由实验结果可知，量化因子在线调节的模糊控制器相比于固定量化因子的模糊控制器，柔顺指标均更优，相对角速度变化更平缓，变构控制的柔顺程度更高，证明了控制算法在柔顺控制上的有效性.

5 结论

1) 为解决磁铰链机构约束下的微纳聚合体卫星变构过程的柔顺控制问题，设计了变构过程的模糊控制器，并在控制器中引入量化因子在线模糊调节器用于改进原控制器以达到更柔顺的控制效果.

2) 变构过程的动力学仿真结果表明，由于磁铰链处阻力矩的存在以及空间多体系统各部分间的动力学耦合，变构过程会受到一定阻碍.

3) 通过数学仿真与气浮台物理仿真实验对控制方法进行验证.验证结果表明:改进后的控制器可抵抗磁铰链阻力矩的影响，成功实现变构；相比于未改进控制器，控制效果柔顺程度明显增强，可减小变构过程中磁铰链脱附的可能性与模块间的碰撞冲击.