2. 上海海事大学 海洋环境与生态模拟研究中心,上海 201306;
3. 河北省桃林口水库管理局,河北 秦皇岛 066400
2. Center for Marine Environmental and Ecological Modelling, Shanghai Maritime University, Shanghai 201306, China;
3. Taolinkou Reservoir Administration, Qinhuangdao 066400, Hebei, China
当前,BASINs/HSPF模型在国内外流域水文水质模拟方面得到了较为广泛的应用[1].评价模型模拟结果不确定性、提升模型模拟精度开始成为模型应用的重要问题.一般而言,模型模拟结果的不确定性取决于模型结构的不确定性、模型参数的不确定性以及模型输入的不确定性等[2].首先,模型结构不确定性一般需要通过模型结构的重新研发、组合(或集合)模型[3]等途径进行优化,前者涉及流域水文水质系统模型的系统开发,而后者则超出了单个流域模型研究的范畴.其次,HSPF模型参数不确定性是当前模型不确定性研究的热点,主要包括用于不确定性分析的贝叶斯理论方法、用于灵敏度分析的方差分解方法以及用于校准优化的启发式智能搜索算法等[2, 4-5],典型方法如灵敏度分析[6]、PEST自动校准[7]、正交极差分析[8]等.在降雨输入研究方面,刘洁等应用降雨随机模拟模型分析了3种降雨情景对东江流域径流的影响[9].该文从降雨情景分析的角度考虑了降雨随机性变化,但并未就其对HSPF模型精度影响作出评估.ZHOU Zhang等则针对气候变化导致的降雨模式变化,应用BASINS-HSPF-CAT建模系统评估其对中国海南尖峰岭热带雨林流域水文过程的影响[10].综上发现,对于HSPF模型降雨输入不确定性对其模拟结果影响的研究还未见相关报道.鉴于降雨是HSPF模型最为重要的输入条件,具有非常大的波动性和随机性.本文针对降雨输入较大的波动性和随机性,应用降雨随机模拟方法来考查其对HSPF模型模拟结果的影响,为HSPF模型的深入应用提供参考和借鉴.
1 研究数据与方法 1.1 研究流域及数据以青龙河流域HSPF模型为研究对象考查降雨输入的影响.青龙河干流总长246 km,流域面积6 340 km2,流域范围大部分在河北省青龙满族自治县、平泉县和宽城县境内,部分隶属辽宁省凌源市和建昌县,其中河北境内3 776 km2,辽宁省境内1 284 km2.受太平洋副热带高压的影响,该流域暴雨多发生在7月下旬—8月上旬,两月雨量约占全年降雨量的60%~70%,最大可达80%.
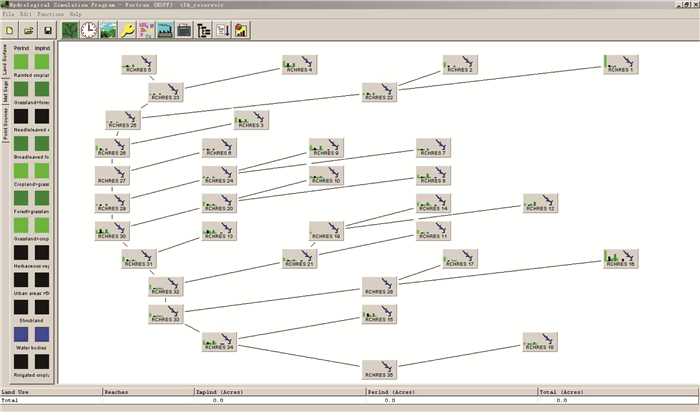
本文研究数据主要包括:1)精度为90 m的SRTM3文件,经ArcGIS10.2处理后可获得流域DEM图;2)应用ArcGIS10.2软件对2009年0.5 m空间分辨率的航拍影像进行目视解译,并按照GlobCover2009数据的分类体系,可获得流域12种土地利用类型数据;3)基于流域DEM数据,应用ArcGIS10.2软件进行流域水文系统分析,包括水流方向提取、水流长度计算、河网分级、河流网络获取、汇流累积量计算以及流域分割(子流域获取)等步骤,从而可获得HSPF建模所需要的河网和子流域.本研究中,将整个流域划分为35个子流域,分别对应35个河段,如图 1所示.4)气象数据来自中国气象科学数据共享中心网站河北省青龙站(东经118.950°,北纬40.400°),该站点数据包括1957年—2013年逐日降雨、相对湿度、气温、风速、光照、蒸发皿蒸发和气压等.应用WDMUtil程序可将气象数据计算转换为小时数据,生成wdm格式文件可为HSPF模拟使用.本文研究所采用的即为1957年1月1日—2013年9月30日的日降雨数据,数据来源为中国气象科学数据共享中心网站.针对从该网站下载的数据文件,首先利用Surfer软件和Excel对降雨数据进行格式编排以及异常值的修正,然后应用Surfer软件进一步将降雨数据转化为WDM时间序列格式,作为HSPF模型的输入数据.
|
图 1 青龙河流域HSPF模型界面 Fig. 1 Interface of HSPF model for Qinglong River Watershed |
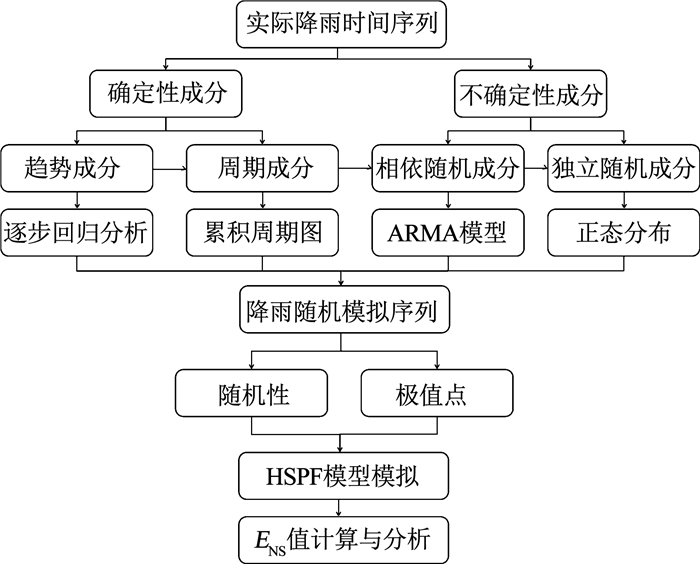
根据随机水文学原理,降雨时间序列包括趋势成分、周期成分、相依随机成分和独立随机成分(白噪声)等.其中,趋势成分和周期成分为降雨时间序列的确定性成分.当降雨时间序列扣除确定性成分后便成为平稳随机序列.该平稳随机序列包括相依随机成分和独立随机成分两个部分.为此,分别对上述各个时间序列成分进行建模,建立降雨时间序列的随机模拟模型,采用蒙特卡洛方法,获得多组降雨随机模拟序列,逐个作为HSPF模型的降雨输入进行模拟,获得每次模拟的Nash-Sutcliffe效率系数(ENS,下同),据此来评价降雨输入对HSPF模型模拟效果的影响.研究技术路线参见图 2.
|
图 2 研究路线 Fig. 2 Research roadmap |
首先分别采用非参数Mann-Kendall趋势检验法、Mann-Kendall秩次相关检验法、Spearman秩次相关检验法、线性回归法以及滑动平均法评估实际降雨时间序列(Z (t))的趋势显著性.然后采用如下方法对降雨时间序列的趋势成分进行建模.降雨时间序列趋势成分可选取为如下形式[11]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat f}}\left( t \right) = {c_0} + \sum\limits_{i = 1}^4 {{c_i}} {t^i} + {c_5}{t^{ - 1}} + {c_6}{t^{ - 2}} + {c_7}{t^{1/2}} + }\\ {{c_8}{t^{ - 1/2}} + {c_9}{{\rm{e}}^{ - t}} + {c_{10}}\ln t.} \end{array} $ | (1) |
式中:t为时间变量,ci(i=0, 1, 2, …, 10)为待定系数.
然后采用逐步回归分析方法确定函数形式.当样本数目很大时,可选用相对的时间单位,即有
| $ {t_0} = 1,\tau = \frac{1}{N},{t_j} = 1 + \frac{j}{N},j = 1,2, \cdots ,N. $ | (2) |
式中:N为样本数目,τ为采样间隔.
1.2.2 周期成分建模方法降雨时间序列的周期项p (t)可表达为d个谐波函数的组合,即
| $ \mathit{\boldsymbol{\hat p}}(t) = \sum\limits_{}^d {\left[ {{a_j}\cos \left( {{w_j} \cdot t} \right) + {b_j}\sin \left( {{w_j} \cdot t} \right)} \right.} . $ | (3) |
式中:
| $ {a_j} = \frac{2}{N}\sum\limits_{i = 1}^N {\left[ {\left( {\mathit{\boldsymbol{Y}}(t) - \mathit{\boldsymbol{\bar Y}}} \right)\cos \left( {{w_j} \cdot t} \right)} \right]} , $ | (4) |
| $ {b_j} = \frac{2}{N}\sum\limits_{t = 1}^N {\left[ {\left( {\mathit{\boldsymbol{Y}}(t) - \mathit{\boldsymbol{\bar Y}}} \right)\sin \left( {{w_j} \cdot t} \right)} \right]} . $ | (5) |
式中,Y (t)= Z (t)- f (t),为实际序列去除趋势项之后的残差序列.
确定谐波个数d可采用累积周期图的方法[12].具体方法如下:
1) 计算序列Y (t), t=1, 2, …, N的方差:
| $ {S^2} = \frac{1}{N}\sum\limits_{t = 1}^N {{{\left( {\mathit{\boldsymbol{Y}}(t) - \mathit{\boldsymbol{\bar Y}}} \right)}^2}} . $ | (6) |
2) 计算第j个谐波对序列方差S2的贡献:
| $ c_j^2 = \frac{1}{2}\left( {a_j^2 + b_j^2} \right),j = 1,2, \cdots ,k. $ | (7) |
当N为偶数时,
为了寻求方差贡献较大的那些谐波,将ci2从大到小依次累加:
| $ {W_m} = \sum\limits_{i = 1}^m {c_i^2} ,m = 1,2, \cdots ,k, $ | (8) |
| $ {B_m} = \frac{{{W_m}}}{{{S^2}}}. $ | (9) |
Bm和m的关系图称为累积周期图.根据累积周期图上拐点的位置判断显著谐波的个数d(当转折点不明显时,一般可以累积贡献率小于90%~95%为临界点进行判断.对于无周期成分的序列,累积解释方差图为一直线),同时计算d个显著谐波所对应的频率
1) 相依随机成分建模方法.实际降雨时间序列去除趋势成分和周期成分后,就可按照平稳时间序列模型进行建模.其中的相依随机成分建模一般采用自回归滑动平均模型(ARMA),包括AR(p)和MA(q)两部分.本文采用最小信息准则(AIC准则和BIC准则)来确定ARMA(p, q)模型阶数p和q,并采用矩法来估计模型参数.相依随机成分的建模表达式一般可以表示为
| $ \begin{array}{*{20}{c}} {s(t) = {\beta _0} + {\beta _1}s(t - 1) + {\beta _2}s(t - 2) + \cdots + {\beta _n}s(t - n) + }\\ {e(t) + {\alpha _1}e(t - 1) + {\alpha _2}e(t - 2) + \cdots + {\alpha _d}e(t - d).} \end{array} $ | (10) |
式中:s(t)和e(t)分别代表自回归模型和滑动平均模型,α和β分别代表相应系数.
2) 独立随机成分(白噪声)建模方法.根据建立的平稳时间序列模型,可以反求残差序列.残差成分的均值应为0,方差可经过统计计算得出.由此就可以确定独立随机成分(白噪声成分)的数学表达形式.残差成分的正态独立性需要在建模后验证.若已知独立随机成分的均值和方差,可按照正态分布对其进行随机模拟.
3) 残差成分的正态独立性检验.进行上述建模后,需要进行残差成分的正态独立性检验,验证所建立的模型是否满足要求,能否反映实际降雨时间序列的时序特性和随机变化规律.
由于平稳序列模型ARMA(p, q)是建立在具有正态概率分布特性的独立随机成分(白噪声成分)基础之上.在模型建立之后,必须对残差成分的独立正态性进行检验.一般采用自相关函数检验法,首先构造统计量:
| $ R = N\sum\limits_{k = 1}^m {r_k^2} . $ | (11) |
若残差序列为独立序列,则统计量R服从自由度为(m-p-q)的χ2分布.公式中m为最大滞时(一般可选取为N/4左右),N为序列长度,rk为残差序列的k阶自相关系数.
检验的步骤:以“残差序列为相互独立序列”作为原假设,选择显著水平α(可取为0.95),取半轴(χα2,∞)为否定域.根据α和自由度(m-p-q)由统计表查出相应的χα2值;然后由残差序列计算出rk(k=1, 2, …, m),通过公式计算出R值;若R≤χα2,则接受原假设,否则拒绝原假设.
1.2.4 降雨时间序列的蒙特卡洛随机模拟方法根据上述获得降雨时间序列趋势成分、周期成分、相依随机成分和独立随机成分即可进行降雨时间序列的计算机蒙特卡洛模拟.其中,趋势成分和周期成分为确定性成分,相依随机成分与初始值设定有关,独立随机成分按照均值为0、方差为δ的正态分布进行随机模拟.降雨时间序列计算机模拟的具体步骤为:①根据式(1)和(3)分别计算趋势成分
根据常用的5种时间序列趋势性检验方法,对青龙河流域的实际降雨时间序列进行分析(见表 1).根据检验结果,Mann-Kendall秩次相关检验法的检验结果为显著,其余4种方法均为不显著.为了保证趋势分析的可靠度,继续通过定量分析的方法识别青龙河流域降雨时间序列的趋势成分.
| 表 1 降雨时间序列趋势检验结果比较 Tab. 1 Comparison of trend test results for rainfall time series |
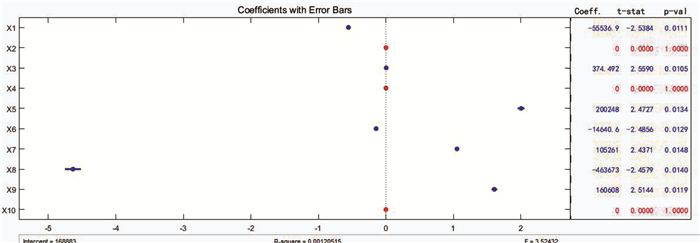
为了定量确定青龙河流域实际降雨时间序列的趋势成分,基于Matlab平台,采用逐步回归分析方法确定其趋势成分,如图 3所示.根据式(1),设定95%置信限,获得趋势成分的拟合公式(见式(11)).根据式(12),获得降雨时间序列的趋势成分,如图 4所示.
| $ f(t) = 0.0267{t^2} + 0.0534{t^{ - 1}} + 0.133\ln t. $ | (12) |
|
图 3 Matlab平台上应用逐步回归分析法优化趋势成分 Fig. 3 Stepwise regression analysis for optimizing trend components on Matlab |

|
图 4 趋势成分建模结果 Fig. 4 Results of trend component modeling |
根据累积周期图建模方法,可以发现实际降雨序列存在约13年的变化周期,与小波分析、功率谱方法获得的周期结果相同.式(13)为实际降雨序列周期成分表达式.周期成分的建模结果如图 5所示.
| $ p(t) = 0.87 + 0.135\cos \left( {\frac{{2{\rm{ \mathit{ π} }}}}{{13}}t} \right) - 0.173\sin \left( {\frac{{2{\rm{ \mathit{ π} }}}}{{13}}t} \right). $ | (13) |

|
图 5 周期成分结果 Fig. 5 Results of periodic component |
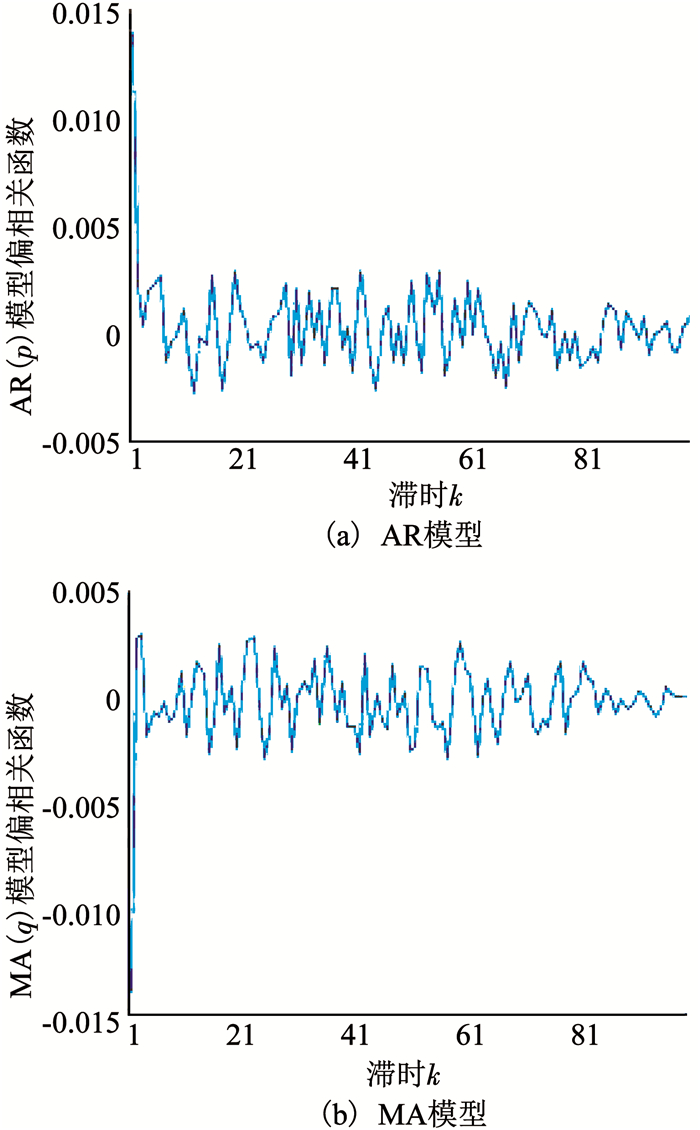
首先根据AR模型以及MA模型的偏相关函数判断ARMA模型的阶次,如图 6所示.然后应用矩法进行参数估计,从而获得3个ARMA模型,如表 2所示.分别计算上述3个模型的AIC值和BIC值,并进行比较.由表 2可知,ARMA(1, 1)模型的AIC值、BIC值最小,故根据最小准则选择其作为相依随机成分的建模形式.
|
图 6 ARMA模型偏相关函数 Fig. 6 Partial correlation function of ARMA model |
| 表 2 ARMA模型优选 Tab. 2 ARMA model optimization |
在实际降雨时间序列扣除趋势成分、周期成分和相依随机成分之后,即可获得残差成分.根据统计分析,残差成分的均值为0,方差为7.953.首先,需要检验残差成分的正态独立性假设是否成立.选取最大滞时m=5 002,检验统计量R=4 994.138,查阅χ2分布表,x1-0.052(5 000)=5 165.615,所以R < 5 165.615.这就说明残差成分满足正态独立性假设,可以采用正态分布对其进行随机模拟.
2.5 随机模拟模型实用性检验为了检验随机模拟序列是否能够反映实际降雨时间序列的大部分统计特性.此处采用长序法对该模型的实用性进行初步分析.检验内容包括均值、离差系数Cv、偏差系数Cs和一阶自相关系数.按相对误差≤10%统计参数通过率,结果见表 3.
| 表 3 统计参数通过率 Tab. 3 Ratio of parameters eligible for verification |
根据表 3中各项统计数据,降雨随机模拟序列通过了长序检验,验证了降雨随机模拟方法及其结果的可信度.这表明,采用趋势成分、周期成分与ARMA建模以及正态随机模拟获得降雨随机模拟序列是量化降雨输入随机性的可行方法.
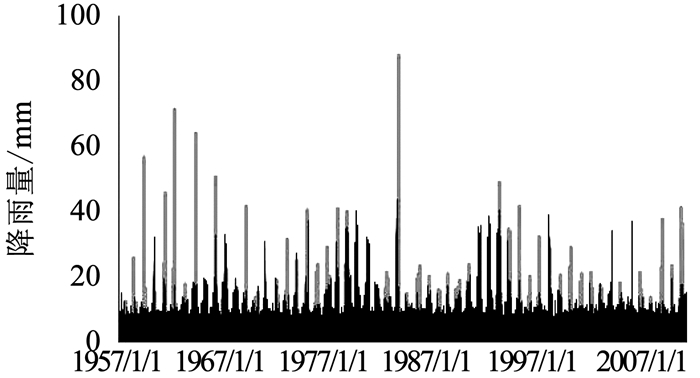
2.6 降雨随机模拟序列生成获得降雨时间序列的趋势成分、周期成分、相依随机成分以及独立随机成分之后,就可以应用蒙特卡罗方法,在计算机上可实现降雨时间序列的随机模拟,获得与实际降雨时间序列统计特性相似的随机模拟序列.图 7所示为200个降雨随机模拟序列与实际降雨时间序列的比较.
|
图 7 降雨随机模拟序列与实际降雨序列的比较 Fig. 7 Comparison of rainfall random simulation series and actual rainfall series |
为了分析降雨时间序列随机性对于青龙河流域HSPF模型模拟效果的影响,将200组降雨随机模拟序列分别输入到HSPF模型中,计算HSPF模型验证期(2011年)实测径流与模拟径流的ENS值,评价模拟效果.
3.1 青龙河流域HSPF模型灵敏参数优化为了合理评价降雨时间序列对HSPF模型模拟结果的影响,首先需要优化HSPF模型参数,保证HSPF模型精度.为此,应用PEST自动校准程序识别出9个最为灵敏的模型参数,然后采用正交极差分析方法优化获得9个参数的校准结果[8],即LZSN为2,INFILT为0.167,AGWRC为0.95,DEEPFR为0.209,BASETP为0.133,AGWETP为0.1,CEPSC为0.27,UZSN为1.35,IRC为0.483.其余不灵敏参数则采用HSPF模型设定默认值,并进行相应参数不确定性的影响分析.
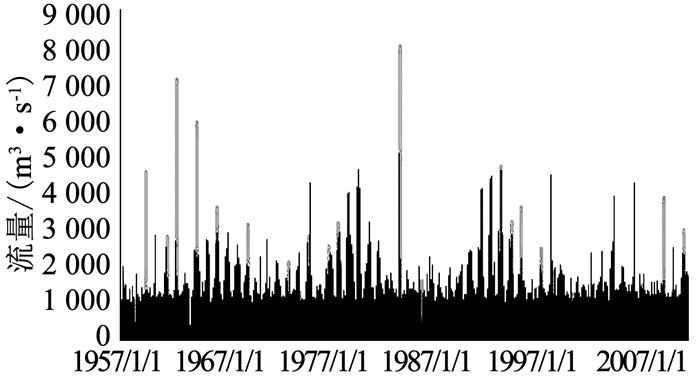
3.2 降雨随机模拟序列对HSPF模型模拟结果的影响将上述获得的200组降雨随机模拟序列分别输入到HSPF模型中运行模拟,可以获得200组模拟径流序列(如图 8所示).并根据2011年实测径流数据与HSPF模型的模拟径流数据,计算获得200组ENS值,如表 4所示.根据表 4,200次HSPF模拟获得的ENS值的变化范围为[71.09%, 74.96%],ENS平均值为73.03%,ENS波动幅度为3.87%.由此可以发现,在模型参数得到较好优化的前提下,降雨时间序列随机性仍会导致HSPF模拟ENS值3.87%的起伏.这表明降雨输入的随机性是影响HSPF模型模拟效果的显著因素,是改善HSPF模型模拟效果的重要考量.
|
图 8 模拟径流序列与实测径流序列比较 Fig. 8 Comparison of the simulated runoff series and the actual runoff series |
| 表 4 HSPF随机模拟的ENS值 Tab. 4 Nash-Sutcliffe efficiency (ENS) values by HSPF stochastic simulations |
由于一般的随机建模方法无法充分还原实际降雨时间序列极值点或将极值点作为奇异点滤除,从而导致随机模拟序列较实际时间序列更为平滑.因此,为了评估降雨时间序列中极值点对HSPF模拟结果的影响,此处在随机模拟序列中考虑将实际降雨时间序列的若干极值点还原,从而考查极值点对HSPF模拟结果的影响.选用3.2节中ENS最高值(74.96%)所对应的降雨随机模拟序列,按照每年中日降雨量由大到小顺序,依次还原1个、2个、3个、4个和5个极值点,分别获得5个对应的降雨随机模拟序列,然后依次输入到HSPF模型中,评估其对模拟结果的影响, 结果如表 5所示.由表 5可知,经过5次还原极大值后,HSPF模拟ENS的最小值为75.35%,均大于没有还原极值的降雨随机模拟序列(其ENS最大值为74.96%),这表明降雨时间序列极大值对于HSPF模拟效果具有显著影响.因此,提高HSPF模拟精度需要关注降雨时间序列极大值点的影响.此外,随着每年还原的日降雨极大值数量从1增长到3时,ENS值逐渐增大,每年还复极大值数量为3时,ENS值达到最大,而后逐渐下降.这说明降雨时间序列还原3个最大极值点时模拟结果最佳.这也启示,在HSPF模拟的降雨情景优选时,还原的极大值点并非越多越好,而是要重点考虑若干最大极值点的影响.
| 表 5 还原的日降雨极值个数与相应的ENS值 Tab. 5 Number of modified daily rainfall extremes and the corresponding ENS values % |
同理,为了考查降雨时间序列极小值点对模拟结果的影响,经过5次还原极小值后,HSPF模拟ENS的最小值为75.03%,也均大于没有还原极值的降雨随机模拟序列(其ENS最大值为74.96%),这表明降雨时间序列极小值点对于模拟结果具有优化作用.然而,还原极小值之后,HSPF模拟的ENS值的波动幅度仅为0.16%,这表明将降雨模拟序列中每年日降雨量的极小值还原后,对于HSPF模型的影响并不显著.此外,随着每年还原的日降雨极小值数量从1增长到4时,ENS值逐渐增大,每年还复极小值数量为4时,ENS值达到最大,而后下降.这说明降雨时间序列还原4个最大极值点时模拟结果最佳.这也启示,在HSPF模拟的降雨情景优选时,还原的极小值点并非越多越好,而是要重点考虑若干最小极值点的影响.
通过降雨输入随机性和极值点对HSPF模型模拟结果的影响分析,发现在模型参数相对优化的条件下,两个因素对于HSPF模型模拟结果影响具有7.33%的贡献率,这表明降雨输入的不确定性是HSPF模型模拟结果不确定性的重要来源,也是提高HSPF模型精度的重要方面.
4 结论1) 采用趋势成分、周期成分与ARMA建模以及正态随机模拟获得降雨随机模拟序列是量化降雨输入随机性的可行方法.
2) 在模型参数优化的条件下,降雨随机模拟序列HSPF模拟ENS值的变化区间为[71.09%, 74.96%],波动幅度达3.87%,表明降雨输入随机性对于HSPF模拟结果具有显著影响.
3) 当考虑每年的日降雨量极大值时,ENS值变化区间为[75.35%, 78.81%],波动幅度达3.46%,且结果均优于没有考虑降雨极值点的降雨随机模拟序列,表明降雨时间序列的极大值对于HSPF模拟效果具有显著影响.
4) 随着降雨时间序列中所考虑极大值点数量的逐渐增多,HSPF模拟效果出现下降趋势,表明HSPF模拟应特别关注若干最大极值点的影响.
5) 当考虑每年的日降雨量极小值时,ENS值变化区间为[75.03%, 75.19%],波动幅度仅为0.16%,表明降雨时间序列的极小值对于HSPF模拟效果的影响并不显著.
6) 降雨输入的不确定性是HSPF模型模拟结果不确定性的重要来源,改善HSPF模拟效果需要考虑降雨时间序列随机性和极值点因素的影响.
本研究可为量化降雨输入对HSPF模型模拟的影响以及HSPF模拟降雨情景的选择提供借鉴.
| [1] |
李兆富, 刘红玉, 李燕. HSPF水文水质模型应用研究综述[J]. 环境科学, 2012, 33(7): 2217. LI Zhaofu, LIU Hongyu, LI Yan. Review on HSPF model for simulation of hydrology and water quality processes[J]. Environmental Science, 2012, 33(7): 2217. DOI:10.13227/j.hjkx.2012.07.022 |
| [2] |
宋晓猛, 占车生, 夏军, 等. 流域水文模型参数不确定性量化理论方法与应用[M]. 北京: 中国水利水电出版社, 2014. SONG Xiaomeng, ZHAN Chesheng, XIA Jun, et al. Quantitative theory method and application of parameter uncertainty for watershed hydrological model[M]. Beijing: China Water Conservancy and Hydropower Press, 2014. |
| [3] |
杨明祥, 雷晓辉, 蒋云钟, 等. 青狮潭水库降水集合预报模式构建及应用[J]. 水利学报, 2018, 49(2): 263. YANG Mingxiang, LEI Xiaohui, JIANG Yunzhong, et al. Construction and application of precipitation ensemble forecast model for Qingshitan Reservoir[J]. Journal of Hydraulic Engineering, 2018, 49(2): 263. DOI:10.13243/j.cnki.slxb.20170683 |
| [4] |
程晓光, 张静, 宫辉力. 半干旱半湿润地区HSPF模型水文模拟及参数不确定性研究[J]. 环境科学学报, 2014, 34(12): 3179. CHENG Xiaoguang, ZHANG Jing, GONG Huili. HSPF hydrologic simulation and parameter uncertainty in a semi-arid and semi-humid area[J]. Acta Scientiae Circumstantiae, 2014, 34(12): 3179. DOI:10.13671/j.hjkxxb.2014.0783 |
| [5] |
庞树江, 王晓燕, 马文静. 多时间尺度HSPF模型参数不确定性研究[J]. 环境科学, 2018, 39(5): 2030. PANG Shujiang, WANG Xiaoyan, MA Wenjing. Research of parameter uncertainty for the HSPF model under different temporal scales[J]. Environmental Science, 2018, 39(5): 2030. DOI:10.13227/j.hjkx.201710070 |
| [6] |
罗川, 李兆富, 席庆, 等. HSPF模型水文水质参数敏感性分析[J]. 农业环境科学学报, 2014, 10: 1995. LUO Chuan, LI Zhaofu, XI Qing, et al. Sensitivity analysis of hydrological and water quality parameters of HSPF model[J]. Journal of Agro-Environment Science, 2014, 10: 1995. DOI:10.11654/jaes.2014.10.017 |
| [7] |
李金城, 常学秀, 高伟. 目标函数权重对PEST-HSPF水文率定的影响研究[J]. 水文, 2017, 37(6): 9. LI Jincheng, CHANG Xuexiu, GAO Wei. Impact of objective function weight on hydrological calibration of PEST-HSPF[J]. Journal of China Hydrology, 2017, 37(6): 9. DOI:10.3969/j.issn.1000-0852.2017.06.002 |
| [8] |
刘兴坡, 陈翔, 胡小婷, 等. 基于正交极差分析的青龙河流域HSPF模型参数寻优模式[J]. 哈尔滨工业大学学报, 2018, 50(2): 131. LIU Xingpo, CHEN Xiang, HU Xiaoting, et al. Orthogonal range analysis-based HSPF parameter optimization pattern for Qinglong River watershed[J]. Journal of Harbin Institute of Technology, 2018, 50(2): 131. DOI:10.11918/j.issn.0367-6234.201607069 |
| [9] |
刘洁, 陈晓宏, 许振成, 等. 降雨变化对东江流域径流的影响模拟分析[J]. 地理科学, 2015, 35(4): 483. LIU Jie, CHEN Xiaohong, XU Zhencheng, et al. The impact of variation in rainfall on runoff in the Dongjiang River Basin[J]. Scientia Geographica Sinica, 2015, 35(4): 483. DOI:10.13249/j.cnki.sgs.2015.04.014 |
| [10] |
ZHOU Zhang, OUYANG Ying, LI Yide, et al. Estimating impact of rainfall change on hydrological processes in Jianfengling rainforest watershed, China using BASINS-HSPF-CAT modeling system[J]. Ecological Engineering, 2017, 105: 87. DOI:10.1016/j.ecoleng.2017.04.051 |
| [11] |
吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003: 153. WU Zhongru. Theory and application of safety monitoring for hydraulic structures[M]. Beijing: Higher Education Press, 2003: 153. |
| [12] |
丁晶, 邓育仁. 随机水文学[M]. 成都: 成都科技大学出版社, 1988: 92. DING Jing, DENG Yuren. Stochastic hydrology[M]. Chengdu: Chengdu University of Science and Technology Press, 1988: 92. |
 2020, Vol. 52
2020, Vol. 52


