移动车辆经过公路桥梁结构时,由于桥头伸缩缝、桥面不平整等外激励,形成车辆桥梁耦合振动系统[1-2].一方面,相比于车辆静载作用,桥梁结构内力会有所增大;另外一方面,桥梁振动与车辆振动会使桥上行人与车内乘客舒适性降低.对于前者,国内外桥梁设计规范均通过引入冲击系数的方法来考虑车辆荷载的动力效应;而后者则往往根据加速度限值、自振频率限值与舒适度指标等来确保人们的舒适性,但目前主要针对人行桥梁[3].
近年来,关于冲击系数的研究成果较多[4-9],但由于车辆桥梁耦合振动的复杂性以及公路车辆的随机性,使得该课题始终是国内外的研究重点.各国学者运用理论推导、现场试验、仿真模拟等多种方法,对移动车辆荷载作用下桥梁结构的动力性能进行了研究,但主要集中在冲击系数表达式的建立[10],主要包括4种形式:以跨径L作为自变量的函数,以基频f作为自变量的函数,常数,引入活载恒载比P/G等其他参数的函数.遗憾的是,不同国家的设计规范对于冲击系数的考虑至今尚未达成一致意见,甚至有的规范与其他的相差较大[11];另外,不同学者对冲击系数的认识与阐述有别,为其进一步发展带来了困难.
为此,本文拟从冲击系数的基本概念入手,结合理论推导与仿真模拟的方法,并借助其物理含义,对一些关键问题进行讨论.
1 冲击系数基本概念冲击系数,作为考虑移动车辆荷载对桥梁结构动力响应放大效应的唯一参数,其基本概念十分重要,对桥梁动力性能的设计与评价具有直接影响.
1.1 不同定义方法实际应用过程中,冲击系数定义方法各不相同.通过对既有文献回顾与整理,有如下8个表达式[12]:
| $ {I_1} = \frac{{{\Delta _1}}}{{\delta _{\rm{s}}^ * }},{I_2} = \frac{{{\Delta _3}}}{{{\delta _{{\rm{stat}}}}}},{I_3} = \frac{{{\Delta _4}}}{{{{\delta '}_{{\rm{stat}}}}}},{I_4} = \frac{{{\delta _{\max }} - {\delta _{\min }}}}{{{\delta _{\max }} + {\delta _{\min }}}}, $ |
| $ {I_5} = \frac{{{\delta _{{\rm{dyn}}}} - {\delta _1}}}{{{\delta _1}}} = \frac{{{\delta _{{\rm{dyn}}}}}}{{{\delta _1}}} - 1,{I_6} = \frac{{{\delta _{{\rm{dyn}}}} - {\delta _2}}}{{{\delta _2}}} = \frac{{{\delta _{{\rm{dyn}}}}}}{{{\delta _2}}} - 1, $ |
| $ {I_7} = \frac{{{\delta _{{\rm{dyn}}}} - {\delta _{{\rm{stat}}}}}}{{{\delta _{{\rm{stat}}}}}} = \frac{{{\delta _{{\rm{dyn}}}}}}{{{\delta _{{\rm{stat}}}}}} - 1,{I_8} = \frac{{{\delta _{{\rm{dyn}}}} - {{\delta '}_{{\rm{stat}}}}}}{{{{\delta '}_{{\rm{stat}}}}}} = \frac{{{\delta _{{\rm{dyn}}}}}}{{{{\delta '}_{{\rm{stat}}}}}} - 1. $ |
式中:δstat为车辆慢速过桥时,桥梁响应最大值;δdyn、δmax为车辆正常速度过桥时,桥梁响应的最大值,即最大动响应;δ′stat为中值响应曲线的最大值;δmin为δmax所在周期内的响应最小值;δ1为与δmax所对应的静响应;δ2为与δmax所对应的中值响应;δs*为最大振幅发生时刻对应的桥梁静响应;Δ1为动响应与静响应之差的最大值;Δ3为最大静响应δstat对应时刻动、静响应之差;Δ4为最大中值响应δ′stat对应时刻动、静响应之差.
分析上述8个表达式,涉及到3条曲线,分别为动响应曲线、静响应曲线以及中值响应曲线;I1是以最大振幅进行控制,I2是以最大静挠度进行控制,I3是以最大中值响应进行控制(类似于I2),且均取其对应时刻的静挠度或振幅,具有实际物理意义(与实际情况相符);I4是以最大动响应进行控制,且只运用动响应曲线即可计算,仅考虑最大动响应所在周期部分;I5~I8是以最大动响应进行控制,其中I5与I6的最大静响应分别取为拟静力响应曲线与中值响应曲线对应时刻的值,同样具有实际物理意义;而I7与I8的最大静响应是针对整个曲线的最大值,一般来说不会与最大动响应同时发生,因此不具有实际物理意义.
作为设计而言,要求最大动响应不超过某一限值,因此,前3个表达式是不适用于设计的;I4在实际应用时误差较大,且相当于取了对应时刻的静响应,与I5、I6相类似;中值响应曲线仅仅是静力响应曲线未知情况下的近似取值;因此,最终应选择I7或I8进行实际设计应用,现行规范也是源于此思路.
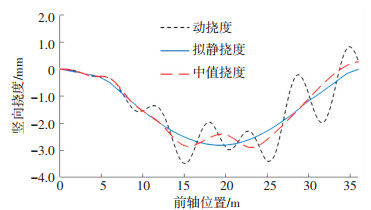
1.2 仿真模拟运用课题组自编程序VBCVA(vehicle-bridge coupled vibration analysis)[13-14],模拟某35 t三轴载重车[15-16]经过跨径为30 m的装配式箱型截面简支梁桥,其中,车辆行驶速度v=20 m/s,桥面平整度等级取很好;由于车辆前轴与后轴之间距离为6 m,因此,从前轴上桥到后轴出桥共行走距离为36 m;另外,以1 m/s的速度过桥获得拟静力曲线,并运用经验模态分解法[17]获得中值响应曲线,仿真结果见图 1~3.
|
图 1 跨中截面挠度曲线 Fig. 1 Deflection curves of mid-span section |
|
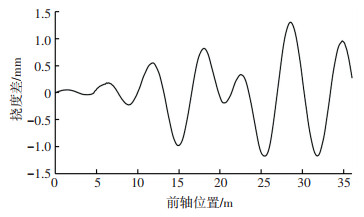
图 2 动挠度与拟静挠度之差 Fig. 2 Differences between dynamic and quasi-static deflections |
|
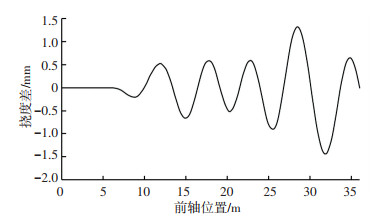
图 3 动挠度与中值挠度之差 Fig. 3 Differences between dynamic and median deflections |
由图 1~3可以得到跨中截面的动、静挠度以及中值挠度等,具体数值见表 1.
| 表 1 跨中截面不同挠度及其差值 Tab. 1 Different deflections of mid-span section and their differentials |
根据表 1,结合上述8个表达式分别计算冲击系数,计算结果为I1=0.591 5,I2=0.094 2,I3=0.083 3,I4=0.441 6,I5=0.384 4,I6=0.230 7,I7=0.239 6,I8=0.203 7.
由此可以看出,采用不同表达式进行冲击系数的计算,其最大值可达0.591 5,而最小值仅为0.083 3,相差非常大,再次说明不可随意选择其中之一进行桥梁的动力性能设计或者评价.另外,跨中截面最大动、静挠度分别为-3.482 8、-2.809 7 mm,显然,根据中国现行规范《公路桥涵设计通用规范(JTG D60—2015)》[18]定义,应选择I7计算所得的冲击系数值0.239 6.
综上所述,目前规范所采用冲击系数只是一个便于设计的中间变量,其合理取值方法可依据I7;而对于现场试验,若不能得到准确静挠度,可近似运用I8来计算,即以中值响应来代替静挠度.
2 挠度冲击系数与弯矩冲击系数的关系在桥梁设计阶段,各国规范均将冲击系数与车辆静载模型的乘积作为设计荷载,进行弯矩(强度)与挠度(刚度)等验算,并未作详细区分.另外,在桥梁动力性能评价时,相比于应变,挠度可更好地反映桥梁整体性能,所以对于跨中截面一般采用挠度曲线进行冲击系数的获取;但对于连续梁的墩顶截面而言,其挠度始终为零,因此只能通过应变曲线来获得冲击系数.可是,由于缺乏弯矩冲击系数与挠度冲击系数之间的关系,往往混为一谈,这将严重阻碍了对桥梁动力性能的客观评价;有时候甚至会造成错误的评价,为桥梁安全埋下隐患.
为此,本文以简支梁为例,分别将车辆简化为单个常量力与两个相等常量力的情况,研究挠度冲击系数与弯矩冲击系数之间的关系.
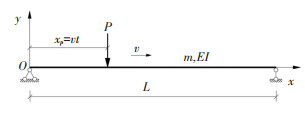
2.1 单个常量力单个常量力P以速度v匀速经过简支梁,简支梁计算跨径为L,单位长度质量为m,截面惯性矩为I,材料弹性模量为E,不计阻尼,计算模型见图 4.
|
图 4 单个常量力经过简支梁 Fig. 4 Simply supported girder under single moving load |
显然,当单个常量力位于简支梁跨中位置时,可得跨中截面静挠度与静弯矩的最大值分别为
| $ {u_{{\rm{bs}},\max }}\left( {\frac{L}{2}} \right) = \frac{{P{L^3}}}{{48EI}}, $ | (1) |
| $ {M_{{\rm{bs}},\max }}\left( {\frac{L}{2}} \right) = \frac{{PL}}{4}. $ | (2) |
根据结构动力学相关理论,其运动方程为
| $ {m_{\rm{b}}}\frac{{{\partial ^2}{u_{\rm{b}}}\left( {x,t} \right)}}{{\partial {t^2}}} + EI\frac{{{\partial ^4}{u_{\rm{b}}}\left( {x,t} \right)}}{{\partial {x^4}}} = P\delta \left( {x - vt} \right). $ | (3) |
假设简支梁振型为正弦函数,运用振型叠加法求解该方程,可得简支梁任意截面动挠度为
| $ {u_{\rm{b}}}\left( {x,t} \right) = \sum\limits_{n = 1}^N {{q_n}} \left( t \right){\varphi _n}\left( x \right) = \sum\limits_{n = 1}^N {{q_n}} \left( t \right)\sin \frac{{n{\rm{ \mathsf{ π} }}x}}{L}. $ | (4) |
相应地,简支梁的动弯矩为
| $ {M_{\rm{b}}}\left( {x,t} \right) = - EI\frac{{{\partial ^2}y}}{{\partial {x^2}}} = EI{\left( {\frac{{\rm{ \mathsf{ π} }}}{L}} \right)^2}\sum\limits_{n = 1}^N {{n^2}} {q_n}(t)\sin \frac{{n{\rm{ \mathsf{ π} }}x}}{L}. $ | (5) |
对于简支梁,其设计控制截面为跨中截面,即x=L/2,且只考虑第一阶振型,则有
| $ {u_{\rm{b}}}\left( {\frac{L}{2},t} \right) = {q_1}(t), $ | (6) |
| $ {M_{\rm{b}}}\left( {\frac{L}{2},t} \right) = EI{\left( {\frac{{\rm{ \mathsf{ π} }}}{L}} \right)^2}{q_1}(t). $ | (7) |
若记q1(t)的最大值为A1,则挠度与弯矩动力放大系数(η=1+μ)之比为
| $ {\eta _{MD}}(x) = \frac{{1 + {\mu _M}}}{{1 + {\mu _D}}} = \frac{{\frac{{{M_{{\rm{b}},\max }}(x,t)}}{{{M_{{\rm{bs}},\max }}(x)}}}}{{\frac{{{u_{{\rm{b}},\max }}(x,t)}}{{{u_{{\rm{bs}},\max }}(x)}}}} = \frac{{{{\rm{ \mathsf{ π} }}^2}EI}}{{{L^2}}}\frac{{{u_{{\rm{bs}},\max }}(x)}}{{{M_{{\rm{bs}},\max }}(x)}}. $ | (8) |
将式(1)、(2)代入式(8),可得
| $ {\eta _{MD}}\left( {\frac{L}{2}} \right) = \frac{{{{\rm{ \mathsf{ π} }}^2}}}{{12}} = 0.82. $ | (9) |
即弯矩冲击系数要小于挠度冲击系数.
对比式(4)与式(5)可以看出,针对同一截面,高阶振型对弯矩的影响要大于对挠度的影响.若考虑高阶振型,第二阶振型对跨中截面无贡献,因此考虑前三阶振型,即N=3,则有
| $ {u_{\rm{b}}}\left( {\frac{L}{2},t} \right) = {q_1}(t) - {q_3}(t), $ | (10) |
| $ {M_{\rm{b}}}\left( {\frac{L}{2},t} \right) = EI{\left( {\frac{\pi }{L}} \right)^2}\left[ {{q_1}(t) - 9{q_3}(t)} \right]. $ | (11) |
显然,式(10)中的q1(t)- q3(t)与式(11)中的q1(t)-9q3(t)最大值是不相等的,即无法得到式(6)简单形式的结果.但至少可以说明,弯矩冲击系数与挠度冲击系数是不相同的,具体关系只能依赖于仿真模拟.
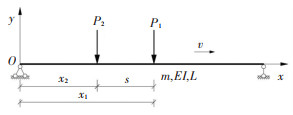
2.2 两个常量力当两个常量力经过简支梁时,假设其间距为s(s≤0.5L),且大小相等,计算模型见图 5.
|
图 5 两个常量力经过简支梁 Fig. 5 Simply supported girder under two moving loads |
简支梁跨中截面静挠度与静弯矩最大值分别为
| $ {u_{{\rm{bs}},\max }}\left( {\frac{L}{2}} \right) = \frac{P}{{24EI}}\left( {2{s^3} - 3L{s^2} + {L^3}} \right), $ | (12) |
| $ {M_{{\rm{bs}},{\rm{max}}}}\left( {\frac{L}{2}} \right) = \frac{1}{2}P\left( {L - s} \right). $ | (13) |
将式(12)、(13)代入式(8),得其比值ηMD为
| $ {\eta _{MD}} = \frac{{1 + {\mu _M}}}{{1 + {\mu _D}}} = \frac{{{{\rm{ \mathsf{ π} }}^2}}}{{12}}\left[ {1 + \frac{s}{L} - 2{{\left( {\frac{s}{L}} \right)}^2}} \right]. $ | (14) |
显然,当式(14)中的间距s=0时,即单个常量力作用,二者比值为0.82,与式(9)完全一致.
为便于表述,若记两常量力的间距与跨径之比值为rs=s/L(0≤rs≤0.5),则有
| $ \frac{{\partial {\eta _{MD}}}}{{\partial {r_{\rm{s}}}}} = 1 - 4{r_{\rm{s}}}. $ | (15) |
令式(15)为零,得rs=0.25,即当两常量力间距s=0.25L时,取得极大值0.93.根据式(14)、(15)可以看出,两个常量力作用下,其比值取值为
| $ 0.82 \le {\eta _{MD}} \le 0.93. $ | (16) |
因此,作为设计指标,可选择较为保守的挠度冲击系数;但作为评价指标,应将挠度冲击系数与弯矩冲击系数分别考虑.
2.3 仿真模拟上述式(9)与式(16)所得结论,均基于只考虑第一阶振型的假设.本节采用有限元程序ANSYS对单个常量力、两个常量力经过简支梁进行仿真模拟,来进一步确定弯矩与挠度冲击系数之间的关系.
2.3.1 单个常量力简支梁的跨径为40 m,弹性模量为3.45×104 MPa,抗弯惯性矩为0.235 6 m4,密度为2 500 kg/m3,截面面积为0.5 m2,不计阻尼,单个常量力P=30 t,移动速度分别为5、10、15、20 m/s.根据结构静力学理论,可计算得跨中截面静挠度、静弯矩最大值分别为-4.92 cm、3 000 kN·m.动力计算结果见表 2.
| 表 2 单个常量力经过简支梁计算结果 Tab. 2 Calculation results of simply supported girder under single moving load |
由表 2可以看出,弯矩M与挠度D的动力放大系数之比ηMD均大于式(9)中的0.82,再次说明高阶振型对动弯矩的贡献要大于对动挠度的贡献.而且,当速度为15 m/s时,二者相差高达10%,值得注意.
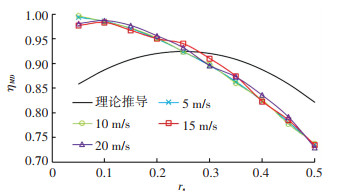
2.3.2 两个常量力简支梁基本参数同上,两个常量力分别为P1=P2= 15 t,移动速度取5~20 m/s,间距为2~10 m.其中,静力响应最大值依然可以通过式(12)、(13)计算,而动力响应最大值则需运用ANSYS分析,两个常量力在不同间距不同移动速度作用下简支梁跨中截面挠度与弯矩动力放大系数计算结果见表 3,其理论推导与仿真模拟结果对比见图 6,表中ηMD-t表示通过理论推导计算的数值,ηMD-s表示通过仿真模拟计算的数值.
| 表 3 两个常量力经过简支梁计算结果 Tab. 3 Calculation results of simply supported girder under two moving loads |
|
图 6 ηMD理论推导与仿真模拟结果对比 Fig. 6 Comparison between theoretical deviation and numerical simulation of ratio ηMD |
由表 3及图 6可以看出,其比值ηMD与两个常量力移动速度基本没有关系,但是与其间距密切相关,随着间距的增大基本呈下降趋势;另外,由于高阶振型的影响,仿真模拟与理论推导结果不完全相同,但弯矩动力放大系数均小于挠度动力放大系数.
综上所述,针对不同响应,其冲击系数并不相同,且弯矩冲击系数往往小于挠度冲击系数;相比于挠度,高阶振型对弯矩的影响较大;对于部分情况,弯矩与挠度冲击系数相差较大,应分别计算.
3 桥梁不同截面对应冲击系数的区别在对桥梁设计或者通过试验评价时,均需首先确定控制截面.对于简支梁桥,一般选择跨中截面;而对于连续梁桥,则较为复杂,不可仅选择中跨跨中截面,应考虑不同截面之间的区别与联系.
本文采用ANSYS建立有限元模型,分析单个常量力经过多跨连续梁时各截面冲击系数的区别.
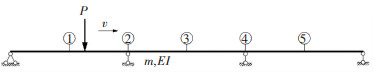
3.1 单个常量力经过三跨连续梁选择跨径布置为40 m×3的三跨连续梁为例,如图 7所示,其截面性质以及材料参数同上,不计阻尼;单个常量力取P=30 t,移动速度为5 ~30 m/s.冲击系数计算结果见表 4和图 8、9.
|
图 7 单个常量力经过三跨连续梁 Fig. 7 Three-span continuous girder under single moving load |
| 表 4 不同截面冲击系数计算结果 Tab. 4 Calculation results of impact factors of different sections |
|
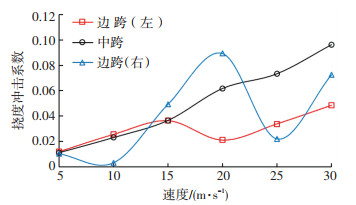
图 8 跨中截面挠度冲击系数 Fig. 8 Impact factors of deflections of mid-span sections |
|
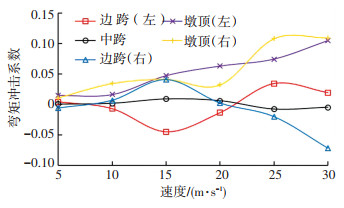
图 9 不同截面弯矩冲击系数 Fig. 9 Impact factors of moments of different sections |
由图 8可以看出,在常见速度范围内,各跨跨中截面挠度冲击系数随着速度的增大基本呈上升趋势,但不同截面受移动速度的影响并不相同;该三跨连续梁为对称结构,但由于常量力移动方向不同,导致即使处于对称位置的两个边跨跨中截面所对应挠度冲击系数也不相同,且相差较大,当移动速度为20 m/s时,右侧边跨冲击系数竟高达左侧边跨的4倍;总体来说,当移动方向为从左向右时,右侧边跨冲击系数要大于左侧边跨,这是由于当常量力移动至右侧边跨时相当于桥梁已经存在初始振动.
由图 9可以看出,弯矩冲击系数与挠度冲击系数具有相同的特点,即随着移动速度的增大基本呈上升趋势以及对称位置冲击系数并不相等.除此之外,值得注意的是,不同截面的弯矩冲击系数从大到小依次排序为墩顶、边跨跨中、中跨跨中, 分析其原因,对于等跨等截面三跨连续梁而言,对中跨跨中截面动力响应起主要贡献的是第一阶振型,而对边跨跨中截面、墩顶截面则分别为第二阶、第三阶振型,显然,高阶振型对应频率较高,根据式(5)可知,其影响也较大.
因此,单个常量力作用于三跨连续梁,其不同截面对应冲击系数并不相同,且有时相差较大,值得注意,不可笼统地使用一个冲击系数值.
3.2 单个常量力经过多跨连续梁根据常见桥梁,选择2~6跨的多跨连续梁(单跨跨径均为40 m),其他参数同上,单个常量力为取P=30 t,移动速度为20 m/s.需要说明的是,常量力移动方向均为从左向右,各跨跨中编号与各墩墩顶截面编号见图 10.各跨跨中截面挠度冲击系数计算结果见表 5,各墩墩顶截面弯矩冲击系数计算结果见表 6.
|
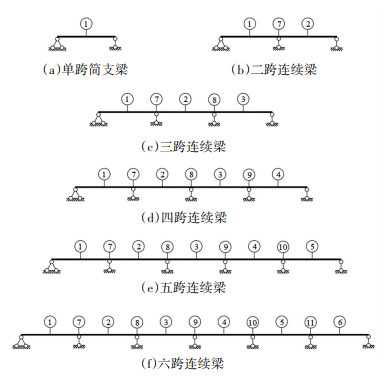
图 10 单跨简支梁与多跨连续梁示意图 Fig. 10 Schematic diagram of simply supported girder and multi-span continuous girders |
| 表 5 各跨跨中截面挠度冲击系数 Tab. 5 Impact factors of deflections in mid-span section |
| 表 6 各墩墩顶截面弯矩冲击系数 Tab. 6 Impact factors of moment in pier-top section |
从表 5、6可以看出,对于奇数跨连续梁(包括单跨简支梁),中跨跨中截面挠度冲击系数随着跨数的增加而减小;对于偶数跨连续梁,中墩墩顶截面弯矩冲击系数随着跨数的增加也减小.虽然等跨径等截面多跨连续梁桥与对应跨径的单跨简支梁桥基频相等[19],但考虑高阶振型的影响,随着跨数的增加,对于中跨或者中墩而言,其相当于加强了约束作用,刚度增大,而最终导致动力性能有所改善,即冲击系数减小.但需要强调的是,除中跨以外,其余跨对应的冲击系数该规律并不明显.
另外,相比于多跨连续梁,单跨简支梁跨中截面挠度冲击系数最大,说明其动力性能较差,这也是最近几年较多简支转连续桥梁取代了简支梁的缘故;当然,还有一个原因是多跨连续梁伸缩缝较少,提高了行车舒适性.
由表 5可以看出,当常量力从左向右移动时,处于对称位置的截面对应冲击系数,大多数时候,左侧要小于右侧,这与上述三跨连续梁时所得结论一致.另外,即使对于六跨连续梁,除边跨以外的各跨约束条件接近,但其结果仍然相差较大,再次说明不同截面对应冲击系数不相等,应加以重视.
对比表 5、6,墩顶截面弯矩冲击系数普遍大于跨中截面挠度冲击系数,同样与高阶振型有关.
综上所述,多跨连续梁的动力性能要优于单跨梁(简支梁),但其不同截面对应冲击系数不相等,应引起足够重视;一般而言,由于振型贡献的不同,墩顶冲击系数最大,边跨次之,中跨最小;处于对称位置的截面,由于初始振动的影响,往往会使后经过的截面冲击系数较大.
4 结论1) 现行规范所采用冲击系数是一个不具有实际物理意义仅便于设计的中间变量,针对冲击系数的定义,对于现场试验,若不能得到准确的静挠度,可近似运用中值响应来代替静挠度.
2) 针对不同响应,其冲击系数并不相同,且弯矩冲击系数往往小于挠度冲击系数;相比于挠度,高阶振型对弯矩的影响较大;对于部分情况,弯矩与挠度冲击系数相差较大,应分别计算.
3) 多跨连续梁的动力性能要优于单跨梁(简支梁),但其不同截面对应冲击系数不相等;一般而言,由于振型贡献的不同,墩顶冲击系数最大,边跨次之,中跨最小;处于对称位置的截面,由于初始振动的影响,往往会使后经过的截面冲击系数较大.
4) 设计与评价所采用冲击系数并不相同,设计冲击系数可采用较为保守的值,而对于评价则须明确各参数的影响规律,否则会造成不客观的评价.
| [1] |
王潮海, 王宗林. 车-桥耦合振动分析的模态综合方法[J]. 公路交通科技, 2006, 23(12): 76. WANG Chaohai, WANG Zonglin. Dynamic analysis on coupled vehicle-bridge system by modal synthesis method[J]. Journal of Highway and Transportation Research and Development, 2006, 23(12): 76. DOI:10.3969/j.issn.1002-0268.2006.12.018 |
| [2] |
李岩, 吴志文, 蔡明, 等. 一种随机车流与桥梁耦合振动的分析方法[J]. 哈尔滨工业大学学报, 2018, 50(3): 46. LI Yan, WU Zhiwen, CAI Ming, et al. An analysis method for coupled vibration random traffic flow and bridge[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 46. |
| [3] |
GAO Qingfei, WANG Zonglin, GUO Binqiang, et al. Design on dynamic performance of highway bridges to moving vehicular loads[J]. Key Engineering Materials, 2014, 574: 43. |
| [4] |
邓露, 何维, 俞扬, 等. 公路车-桥耦合振动的理论和应用研究进展[J]. 中国公路学报, 2018, 31(7): 38. DENG Lu, HE Wei, YU Yang, et al. Research progress in theory and applications of highway vehicle-bridge coupling vibration[J]. China Journal of Highway and Transport, 2018, 31(7): 38. DOI:10.3969/j.issn.1001-7372.2018.07.003 |
| [5] |
朱志辉, 赵婷婷, 王力东, 等. 基于随机振动模型的重载铁路拱桥吊杆应力冲击系数研究[J]. 振动工程学报, 2017, 30(6): 955. ZHU Zhihui, ZHAO Tingting, WANG Lidong, et al. Stress impact factor of the suspenders of heavy-haul railway arch bridge based on random vibration model[J]. Journal of Vibration Engineering, 2017, 30(6): 955. |
| [6] |
徐文涛, 张建波, 廖敬波, 等. 随机振动下多跨弹性支撑梁桥的冲击系数分析[J]. 振动与冲击, 2017, 36(3): 119. XU Wentao, ZHANG Jianbo, LIAO Jingbo, et al. Impact coefficients analysis for a multi-span elastically supported bridge under random vibration[J]. Journal of Vibration and Shock, 2017, 36(3): 119. |
| [7] |
丁勇, 俞丹波, 邹毓颖, 等. 车辆-模数式伸缩缝耦合振动与冲击荷载分析[J]. 中国公路学报, 2018, 31(7): 167. DING Yong, YU Danbo, ZOU Yuying, et al. Analysis of impact load and coupling vibration of vehicle and modular bridge expansion joint[J]. China Journal of Highway and Transport, 2018, 31(7): 167. DOI:10.3969/j.issn.1001-7372.2018.07.015 |
| [8] |
冀伟, 邓露, 何维. 波形钢腹板PC箱梁桥的车桥耦合振动分析及动力冲击系数计算[J]. 振动工程学报, 2016, 29(6): 1041. JI Wei, DENG Lu, HE Wei. Vehicle-bridge couples vibration analysis and calculation of dynamic impact factor for the PC box-girder bridge with corrugated steel webs[J]. Journal of Vibration Engineering, 2016, 29(6): 1041. |
| [9] |
桂水荣, 张政韬, 陈水生, 等. 桥面不平引起车桥系统随机振动车速因素分析[J]. 振动、测试与诊断, 2018, 38(6): 1223. GUI Shuirong, ZHANG Zhengtao, CHEN Shuisheng, et al. Influence analysis of vehicle speeds on random vibration of vehicle-bridge coupling systems caused by deck irregularity[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(6): 1223. |
| [10] |
BANGASH M Y H. Prototype bridge structures: analysis and design[M]. London: Thomas Telford, 1999.
|
| [11] |
MCLEAN D I, MARSH M L. Dynamic impact factors for bridges[M]. Washington DC: Transportation Research Board, 1998.
|
| [12] |
BAKHT B. Review of dynamic testing of Highway Bridges[M]. Ottawa: Ontario Ministry of Transportation, 1989.
|
| [13] |
郭斌强.移动车辆作用下斜拉桥行车舒适性研究[D].哈尔滨: 哈尔滨工业大学, 2013 GUO Binqiang. Study on driving comfort of cable-stayed bridges with moving vehicles[D]. Harbin: Harbin Institute of Technology, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10213-1014003084.htm |
| [14] |
高庆飞.移动车辆荷载作用下梁式桥动力性能设计与评价方法[D].哈尔滨: 哈尔滨工业大学, 2015 GAO Qingfei.Design and evaluation methods on dynamic performance of girder bridges under moving vehicle loads[D]. Harbin: Harbin Institute of Technology, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957513.htm |
| [15] |
王宗林, 高庆飞, KOHC G, 等. 移动车辆荷载作用下大跨径连续梁桥动力响应研究[J]. 桥梁建设, 2015, 45(2): 46. WANG Zonglin, GAO Qingfei, KOH C G, et al. Dynamic responses of long span continuous girder bridge under action of moving vehicle loads[J]. Bridge Construction, 2015, 45(2): 46. |
| [16] |
韩万水, 王涛, 李永庆, 等. 基于模型修正梁格法的车桥耦合振动分析系统[J]. 中国公路学报, 2011, 24(5): 47. HAN Wanshui, WANG Tao, LI Yongqing, et al. Analysis system of vehicle-bridge coupling vibration with grillage method based on model updating[J]. China Journal of Highway and Transport, 2011, 24(5): 47. |
| [17] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and nonstationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903. DOI:10.1098/rspa.1998.0193 |
| [18] |
中华人民共和国交通运输部.公路桥涵设计通用规范: JTG D60—2015[S].北京: 人民交通出版社股份有限公司, 2015 Ministry of Transport of the People's Republic of China. General specifications for design of Highway Bridges and Culverts: JTG D60—2015[S]. Beijing: China Communications Press Co., Ltd., 2015 |
| [19] |
GAO Qingfei, WANG Zonglin, LIU Yang, et al. Modified formula of estimating fundamental frequency of girder bridge with uniform cross-section[C]// Advances in Intelligent Transportation System and Technology. Zurich, Switzerland: Trans Tech Publications Ltd., 2012: 177
|
 2020, Vol. 52
2020, Vol. 52


